Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

CHAPTER 8

Limits of Functions

8.1. Limits of Functions

There are several reasonable deﬁnitions for the limit of a sequence of func-

tions. Clearly the entries of the sequence should approximate the limit function

f to greater and greater accuracy in some sense. But there are different ways of

measuring the accuracy of an approximation, depending on the problem. Different

approximation schemes generally correspond to different norms, although not all

convergence criteria come from a norm. In this section, we consider two natural

choices and see why the stronger notion is better for many purposes.

8.1.1. DEFINITION. Let (f

) be a sequence of functions from S ⊂ R

into

. This sequence converges pointwise to a function f if

lim

n→∞

(x) = f (x) for all x ∈ S.

This is the most obvious and perhaps simplest notion of convergence. It is also

a rather weak concept fraught with difﬁculties.

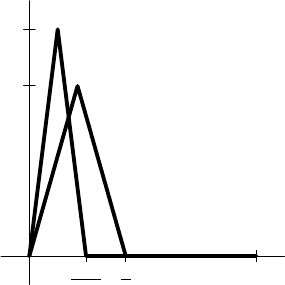
8.1.2. EXAMPLE. Deﬁne piecewise linear continuous functions f

on [0, 1] by

connecting the points (0, 0), (

, n), (

, 0), and (1, 0) by straight lines, namely

(x) =











x for 0 ≤ x ≤

(

− x) for

≤ x ≤

0 for

≤ x ≤ 1.

See Figure 8.1. This sequence converges pointwise to the zero function; that is,

lim

n→∞

(x) = 0 for all 0 ≤ x ≤ 1.

Indeed, at x = 0, we have f

(x) = 0 for all n ≥ 1; and if x > 0, then there is an

integer N such that x ≥ 2/N. Thus once n ≥ N, we have f

(x) = 0. So at every

213

214 Limits of Functions

n+1

n + 1

FIGURE 8.1. Graphs of f

and f

n+1

point, the functions are eventually constant. Notice, however, that the closer x is to

zero, the larger the choice of N must be.

The limit is a continuous function. However, the limit of the integrals is not

the integral of the limit. The area between the graph of f

and the x-axis forms a

triangle with base 2/n and height n and thus has area 1. Therefore,

lim

n→∞

(x) dx = lim

n→∞

1 = 1 6= 0 =

0dx.

In fact, an easy modiﬁcation of this example would yield functions converging

pointwise to 0 with integrals tending to inﬁnity or any ﬁnite value or oscillating

wildly.

The other notion of convergence that we study, uniform convergence, will de-

mand that convergence occur at a uniform rate on the whole space S. To formulate

this, we ﬁrst consider the ε–N version of pointwise limit ﬁrst. A sequence (f

)

converges pointwise to f if for every x ∈ S and ε > 0, there is an integer N so that

(x) − f(x)k < ε for all n ≥ N.

In this case, N depends on both ε and on the point x. (Think about how you would

choose N for different x ∈ [0, 1] in Example 8.1.2.) Uniform convergence demands

that this choice depend only on ε, providing a common N that works for all x in S

simultaneously.

8.1.3. DEFINITION. Let (f

) be a sequence of functions from S ⊂ R

into

. This sequence converges uniformly to a function f if for every ε > 0, there

is an integer N so that

(x) − f(x)k < ε for all x ∈ S and n ≥ N.

8.1 Limits of Functions 215

f + ε

f − ε

FIGURE 8.2. Graph of neighbourhood of f and a sample f

To understand this deﬁnition, look at Figure 8.2. The point is that the graph of

must lie between the graphs of f + ε and f − ε.

Clearly, if (f

) converges uniformly to f, then (f

) also converges pointwise

to f. But this is not reversible.

As we have seen in Example 7.1.3, when K is a compact subset of R

, we may

deﬁne a norm on the space C(K) of all continuous functions on K by

kfk

∞

= sup

x∈K

|f(x)|.

This is deﬁned because the Extreme Value Theorem guarantees that the supremum

is ﬁnite.

When S is a subset of R

that is not compact, there are unbounded continu-

ous functions on S. Nevertheless, we may restrict ourselves to the space C

(S)

consisting of all bounded continuous functions from S to R. Then the supremum

becomes a norm in the same manner. Similarly, we may consider bounded contin-

uous functions with values in R

. This space is denoted C

(S, R

) and has the

norm

kfk

∞

= sup

x∈S

kf(x)k

where k · k

is the usual Euclidean norm in R

. We have the following theorem.

8.1.4. THEOREM. For a sequence of functions (f

) in C

(S, R

), (f

) con-

verges uniformly to f if and only if

lim

n→∞

− fk

∞

= 0.

After the preceding discussion, the proof is immediate. Indeed, the statement

(x) − f(x)k ≤ ε for all x ∈ S is equivalent to saying

− fk

∞

≤ ε.

Returning to Example 8.1.2, the maximum of f

occurs at

with f

(

) = n

and hence

− 0k

∞

= n.

This does not converge to 0. So f

does not converge uniformly to the zero function

(or any other bounded function, for that matter).

216 Limits of Functions

8.1.5. EXAMPLE. Consider f

(x) = x

for x ∈ [0, 1]. It is easy to check that

lim

n→∞

(x) = lim

n→∞

(

0 for 0 ≤ x < 1

1 for x = 1.

Thus the pointwise limit is the function

{1}

, the characteristic function of the

point {1}. The functions f

are polynomials, and hence not only continuous but

even smooth; while the limit function has a discontinuity at the point 1.

For each n ≥ 1, we have f

(1) = 1 and so

−

{1}

∞

= sup

0≤x<1

− 0| = 1.

So f

does not converge in the uniform norm. Indeed, to contradict the deﬁnition,

take ε = 1/2. For each n, let x

= 2

−1/2n

. Then

) −

{1}

)

√

> ε.

Hence there is no integer N satisfying the deﬁnition.

8.1.6. EXAMPLE. Consider the functions f

on [0, π] given by

(x) =

sinnx.

Several of the f

are graphed in Figure 8.3. By the Squeeze Theorem,

lim

n→∞

sinnx = 0 for all 0 ≤ x ≤ π.

Moreover, kf

∞

= sup

0≤x≤π

|sinnx| =

. Thus this sequence converges uni-

formly to 0. If ε > 0, we may choose N so large that

< ε. Then for any

n ≥ N ,

(x) − 0| =

sinnx

≤

< ε for all 0 ≤ x ≤ π.

This sequence does not behave well with respect to derivatives—a typical fea-

ture of uniform approximation. Compute

(x) = cos nx.

Hence lim

n→∞

(0) = lim

n→∞

1 = 1 6= 0 = f

(0); while lim

n→∞

(π) = lim

n→∞

(−1)

does not even exist. Indeed, this limit does not exist at any point of [0, π] except 0.

The intuition is that for any nice smooth function, there are functions that os-

cillate up and down very rapidly and yet remain close to the nice function, such as

our previous functions. The sequence g

(x) =

sinn

x converges uniformly to 0

as well, yet has derivatives, g

(x) = n cosn

x, which do not converge anywhere.

So uniform convergence does not give control of derivatives.

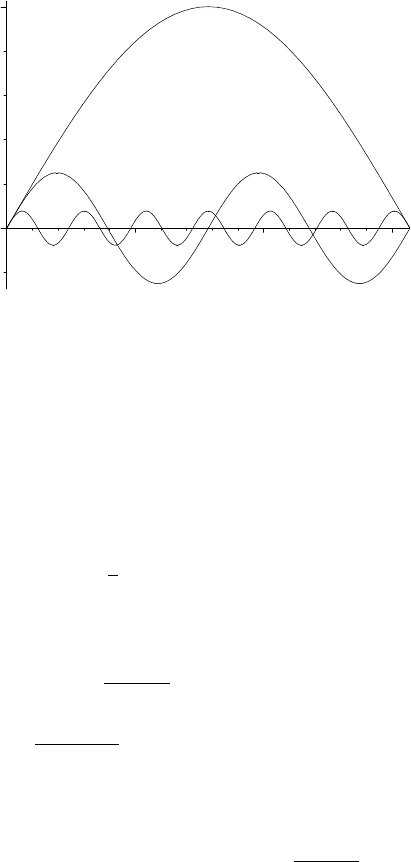
8.1 Limits of Functions 217

2 3

FIGURE 8.3. The graphs of f

for n = 1, 4, and 13.

Exercises for Section 8.1

A. Let f

(x) = xne

−nx

for all x ≥ 0 and n ≥ 1. Show that (f

) converges to zero on

[0, ∞) pointwise but not uniformly.

B. Let f

(x) = nx(1 − x

)

on [0, 1] for n ≥ 1.

Find f(x) = lim

n→∞

(x). Is this convergence uniform?

HINT: Recall that lim

n→∞

(1 −

)

= e

−h

C. For the sequence of functions in the previous exercise, compare the limit of the inte-

grals (from 0 to 1) with the integral of the limit.

D. Does the sequence f

(x) =

1 + nx

converge uniformly on R?

E. Show that f

(x) =

tan

−1

(nx)

, n ≥ 1 converges uniformly on R.

F. Show that f

(x) = n sin(x/n) converges uniformly on [−R, R] for any ﬁnite R but

does not converge uniformly on R.

G. Find all intervals on which the sequence f

(x) =

n + x

, n ≥ 1, converges uni-

formly.

H. Suppose that f

: [0, 1] → R is a sequence of C

functions (i.e., functions with

continuous derivatives) that converges pointwise to a function f. If there is a constant

M so that kf

∞

≤ M for all n, then prove that (f

) converges to f uniformly.

I. Prove Dini’s Theorem: suppose that f and f

are continuous functions on [a, b] such

that f

≤ f

n+1

for all n ≥ 1 and (f

) converges to f pointwise. Prove (f

) converges

to f uniformly.

HINT: Work with g

= f − f

, which decrease to 0. Show that for any point x

and ε > 0, there is an integer N and a positive r > 0 such that g

(x) ≤ ε on

−r, x

+ r). If convergence is not uniform, say limkg

∞

= d > 0, ﬁnd x

such

that limg

) = d. Obtain a contradiction.

218 Limits of Functions

J. Find an example that shows Dini’s Theorem is false if [a, b] is replaced with a non-

compact subset of R.

K. (a) Suppose that f : R → R is uniformly continuous. Let f

(x) = f(x + 1/n). Prove

that f

converges uniformly to f on R.

(b) Does this remain true if f is just continuous? Prove it or provide a counterexample.

L. For which values of x ≥ 1 does the expression x

make sense?

HINT: Deﬁne f

(x) = x and f

n+1

(x) = x

(x)

for n ≥ 1. Then

(a) Show that f

n+1

(x) ≥ f

(x) for all n ≥ 1.

(b) When L(x) = lim

n→∞

(x) exists, ﬁnd optimal upper bounds for x and L.

(x) is bounded above by e for all

n ≥ 1. What can you conclude?

(d) What happens for larger x?

M. The behaviourof x

when 0 < x < 1 is more complicated and so more interesting.

To get started, compute f

(1/16) for small values of n, using the functions f

from

the previous exercise, and see what occurs.

8.2. Uniform Convergence and Continuity

Our ﬁrst positive result is that uniform convergence preserves continuity and

so is (almost) always the right notion of convergence for continuous functions.

8.2.1. THEOREM. Let (f

) be a sequence of continuous functions mapping

a subset S of R

into R

that converges uniformly to a function f. Then f is

continuous.

PROOF. Fix a point a ∈ S and an ε > 0. We must control kf(x) − f(a)k only by

controlling the bound on kx − ak. To this end, we make use of the proximity of

one of the continuous functions f

and compute

kf(x) − f(a)k = kf(x) − f

(x) + f

(x) − f

(a) + f

(a) − f(a)k

≤ kf (x) − f

(x)k + kf

(x) − f

(a)k + kf

(a) − f(a)k.

Note that the ﬁrst and last terms may be controlled by

kf(x) − f

(x)k ≤ kf

− fk

∞

for all x ∈ S,

including the point x = a. The middle term may be controlled by the continuity of

To be precise, ﬁrst choose n so large that

− fk

∞

Then using the continuity of f

at a, choose a positive number r > 0 such that

(x) − f

(a)k <

for all kx − ak < r.

8.2 Uniform Convergence and Continuity 219

Then for all x ∈ S with kx − ak < r, we obtain

kf(x) − f(a)k ≤ kf(x) − f

(x)k + kf

(x) − f

(a)k + kf

(a) − f(a)k

= ε.

Thus f is continuous. ¥

Note that in this proof, smaller values of ε require using a closer approximant

in order to achieve the desired estimate.

Now we will use the compactness of K and Theorem 8.2.1 to show that C(K)

is complete. Just as we used completeness to understand the real line, we can use

it to understand other spaces. First, of course, we have to prove that the space is

complete.

8.2.2. COMPLETENESS THEOREM FOR C(K).

If K is a compact set, the space C(K) of all continuous functions on K with the

sup norm is complete.

PROOF. A sequence (f

) in C(K) is a Cauchy sequence for the sup norm if for

every ε > 0, there is an integer N so that

− f

∞

< ε for all m, n ≥ N.

We must show that every Cauchy sequence has a (uniform) limit in C(K).

First consider an arbitrary point x ∈ K. We have

(x) − f

(x)| ≤ kf

− f

∞

< ε for all m, n ≥ N.

Hence the sequence (f

(x))

∞

n=1

is a Cauchy sequence of real numbers. Since R is

complete, this has a pointwise limit

f(x) := lim

n→∞

(x).

This must be shown to converge uniformly. With ε and N as before, we obtain the

estimate

|f(x) − f

(x)| = lim

n→∞

(x) − f

(x)| ≤ ε for all m ≥ N.

Since this holds for all x ∈ K, it follows that kf −f

∞

≤ ε. Therefore, the limit

is uniform.

By the previous theorem, the uniform limit of continuous functions is continu-

ous. Thus f is continuous and hence belongs to C(K). This establishes that C(K)

is complete. ¥

We have used this method of proof before and will use it again; for example,

Theorem 4.2.5, showing the completeness of R

, and Theorem 8.4.7, later in this

chapter, both follow a similar strategy.

220 Limits of Functions

Exercises for Section 8.2

A. Find the limits of the following functions. Find an interval on which convergence is

uniform and another on which it is not. Explain.

(a) f

(x) =

(b) g

(x) =

2 + 5nx

B. Show that h

(x) =

n + x

4n + x

converges uniformly on [0, N] for any N < ∞ but not

uniformly on [0, ∞).

C. Consider a sequence of continuous functions f

: (0, 1) → R. Suppose there is a

function f : (0, 1) → R so that whenever 0 < a < b < 1, f

converges uniformly on

[a, b] to f. Prove that f is continuous on (0, 1).

D. Let f

and g

be continuous functions on [a, b]. Suppose that (f

) converges uni-

formly to f and (g

) converges uniformly to g on [a, b]. Prove that (f

) converges

uniformly to fg on [a, b].

E. Suppose that (f

) converge uniformly to f on a compact subset K of R

and that

) converge uniformly on K to a continuous function g such that g(x) 6= 0 for

all x ∈ K. Prove that f

(x)/g

(x) is everywhere deﬁned for large n and that this

quotient converges uniformly to f(x)/g(x) on K.

F. Let f

(x) = tan

−1

(nx)/

√

(a) Find f(x) = lim

n→∞

(x), and show that f

converges uniformly to f on R.

(b) Compute lim

n→∞

(x), and compare this with f

(x).

is uniform? Prove your answer.

G. Suppose that functions f

deﬁned on R

converge uniformly to a function f. Suppose

that each f

is bounded, say by A

. Prove that f is bounded.

H. Suppose that f

in C[0, 1] all have Lipschitz constant L. Show that if f

converges

pointwise to f, then the convergence is uniform and f is Lipschitz with constant L.

I. Give an example of a sequence of discontinuous functions f

that converge uniformly

to a continuous function.

8.3. Uniform Convergence and Integration

A useful feature of uniform convergence is its good behaviour with respect to

limits. We now show that integration over a compact set respects uniform limits.

8.3.1. INTEGRAL CONVERGENCE THEOREM.

Let (f

) be a sequence of continuous functions on the closed interval [a, b] con-

verging uniformly to f(x) and ﬁx c ∈ [a, b]. Then the functions

(x) =

(t) dt for n ≥ 1

converge uniformly on [a, b] to the function F (x) =

f(t) dt.

8.3 Uniform Convergence and Integration 221

PROOF. The proof is straightforward:

(x) − F (x)| =

(t) − f(t) dt

≤

(t) − f(t)|dt ≤

− fk

∞

≤ |x − c|kf

− fk

∞

≤ (b − a) kf

− fk

∞

This estimate no longer depends on x. Hence

− F k

∞

≤ (b − a)kf

− fk

∞

Since (f

) converges uniformly to f,

lim

n→∞

− F k

∞

≤ (b − a) lim

n→∞

− fk

∞

= 0.

That is, (F

) converges uniformly to F . ¥

This can be reformulated in terms of derivatives as follows.

8.3.2. COROLLARY. Suppose that (f

) is a sequence of continuously differ-

entiable functions on [a, b] such that (f

) converges uniformly to a function g and

there is a point c ∈ [a, b] so that lim

n→∞

) converges

uniformly to a differentiable function f with f(c) = γ and f

= g.

PROOF. By the Fundamental Theorem of Calculus, f

is the unique antiderivative

of f

whose value at c is f

(c). That is,

(x) = f

(t) dt.

By the previous theorem, the sequence of functions F

(x) =

(t) dt for n ≥ 1

converges uniformly to F (x) =

g(t) dt. Since lim

n→∞

lim

n→∞

− (γ + F )k

∞

≤ lim

n→∞

− F k

∞

= 0.

Therefore, (f

) converges uniformly to

f(x) = γ +

g(x) dx.

Finally, the Fundamental Theorem of Calculus shows that f is differentiable and

= g. ¥

Consider a function of two variables f(x, t). Notice that

F (x) =

f(x, t) dt

is a function of x. The previous theorem can be seen as a special case of this

situation, where x is in N and f (t, n) is written as f

(t). It turns out that F

(x)

222 Limits of Functions

equals the integral of ∂f/∂x, but proving it requires some careful estimates. We

begin with a continuity result that is a continuous parameter version of the Integral

Convergence Theorem.

8.3.3. PROPOSITION. Let f(x, t) be a continuous function on [a, b] × [c, d].

Deﬁne F (x) =

f(x, t) dt. Then F is continuous on [a, b].

PROOF. Since f is continuous on a compact set, it is uniformly continuous. There-

fore, given ε > 0, there is a δ > 0 so that |f(x, t) −f(y, t)| < ε/(d −c) whenever

|x − y| < δ. Therefore,

|F (x) − F (y)| =

f(x, t) − f(y, t) dt

≤

|f(x, t) − f(y, t)|dt

≤

d − c

dt = ε.

Thus F is continuous. ¥

8.3.4. LEIBNIZ’S RULE.

Suppose that f(x, t) and

∂

∂x

f(x, t) are continuous functions on [a, b] ×[c, d]. Then

F (x) =

f(x, t) dt is differentiable and

(x) =

∂

∂x

f(x, t) dt.

PROOF. Fix x

∈ [a, b] and let h 6= 0. Observe that

F (x

+ h) − F (x

)

f(x

+ h, t) − f(x

, t)

dt.

Since f(x, t) is a differentiable function of x for ﬁxed t, we may apply the Mean

Value Theorem to obtain a point x(t) depending on t so that |x(t) − x| < h and

f(x

+ h, t) − f(x

, t)

∂

∂x

f(x(t), t).

The Mean Value Theorem does not show that the function x(t) is continuous. How-

ever, in this situation, the left-hand side of this identity is evidently a continuous

function of t, and hence so is the right-hand side ∂f/∂x(x(t), t).

Since f

(x, t) =

∂

∂x

f(x, t) is continuous on a compact set, it is uniformly

continuous. So for ε > 0, we can choose δ > 0 so that

(x, t) − f

(y, t)

d − c