Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

8.3 Uniform Convergence and Integration 223

whenever |x − y| < δ. Therefore, if |h| < δ, then |x(t) − x| < δ; so

F (x

+h)−F (x

)

−

(x, t) dt

f(x

+h, t) − f(x

, t)

− f

(x, t) dt

≤

(x(t), t) − f

(x, t)

≤

d − c

dt = ε.

Since ε > 0 was arbitrary, we obtain

) = lim

h→0

F (x

+ h) − F (x

)

∂

∂x

f(x, t) dt.

8.3.5. EXAMPLE. We will establish the improper integral

∞

−x

dx =

√

For the deﬁnition of improper integral, see Exercise 6.3.S. It is known that the inte-

gral g(u) =

−x

dx cannot be expressed in closed form in terms of the standard

elementary functions. However, the deﬁnite integral can be evaluated in a number

of ways. Here we exploit Leibniz’s rule to accomplish this. The auxiliary function

that we introduce is unmotivated, but the rest of the proof is straightforward.

Before we begin computing, observe that e

−x

is positive and thus g(u) is

monotone increasing. Thus to prove that a limit exists as u tends to +∞, it sufﬁces

to show that g is bounded. However, e

−x

≤ 1 for all x and e

−x

≤ e

−x

when

x ≥ 1. So

g(u) ≤

1ds +

−s

ds = 1 + (e − e

−u

) ≤ 1 + e.

Consequently, J =

∞

−x

dx is deﬁned and ﬁnite.

Consider

f(x) =

−x(1+t

)

1 + t

dt.

Observe that

f(0) =

1 + t

dt = tan

−1

The integrand h(x, t) =

−x(1+t

)

1 + t

is continuous on [0, ∞) × [0, 1]. We deﬁne

(t) = h(x, t) and observe that 0 ≤ h

(t) ≤ e

−x

. Hence h

converges uniformly

to h

∞

(t) = 0 on [0, 1] as x → +∞. By the Integral Convergence Theorem, we

conclude that

lim

x→∞

f(x) =

lim

x→∞

(t) dt =

0dt = 0.

224 Limits of Functions

Now apply the Leibniz Rule to compute

(x) =

∂

∂x

−x(1+t

)

1 + t

−x(1+t

)

(−(1 + t

))

1 + t

dt = −e

−x

−xt

Make the change of variables s =

√

xt (where x is held constant!), to obtain

(x) = −e

−x

√

−s

√

ds = −

−x

√

x).

Next evaluate f(0) in two ways:

= lim

n→∞

f(0) − f(n) = lim

n→∞

−

(x) dx = lim

n→∞

−x

√

x) dx

Substitute s =

√

x. By the Fundamental Theorem of Calculus, g

(s) = e

−s

. So

= lim

n→∞

√

−s

g(s) ds

= lim

n→∞

√

(s)g(s) ds = lim

n→∞

(s)

= J

Therefore, J =

√

π/2.

Exercises for Section 8.3

A. For x ∈ [−1, 1], let F (x) =

x(1 − x

)

−1/2

dy. Show that F

(x) = (1 − x

)

−1/2

and deduce that F (x) = arcsin(x).

B. For n ≥ 1, deﬁne functions f

on [0, ∞) by

(x) =











−x

for 0 ≤ x ≤ n

−2n

+ n − x) for n ≤ x ≤ n + e

0 for x ≥ n + e

(a) Find the pointwise limit f of f

. Show that the convergence is uniform on [0, ∞).

(b) Compute

∞

f(x) dx and lim

n→∞

∞

(x) dx.

C. Suppose that g ∈ C[0, 1] and (f

) is a sequence in C[0, 1] that converges uniformly to

f. Prove that

lim

n→∞

(x)g(x) dx =

f(x)g(x) dx.

D. Compute lim

n→∞

sinnx

dx.

HINT: Find the limit of the integral over [ε, π] and estimate the rest.

8.4 Series of Functions 225

E. Deﬁne f(x) =

sinxt

dt.

(a) Prove that this integral is deﬁned.

(b) Compute f

(x) explicitly.

is continuous at 0.

F. Deﬁne the Bessel function J

by J

(x) =

−1

cos(xt)

√

1 − t

dt. Prove that J

satisﬁes

the differential equation y

+ y

/x + y = 0, that is, J

+ J

/x + J

is identically zero.

G. With the setup for the Leibniz Rule, let b be a variable and set F (x, b) =

f(x, t) dt.

Let b(x) be a differentiable function, and deﬁne G(x) = F (x, b(x)) =

b(x)

f(x, t) dt.

Show that G

(x) =

b(x)

∂f

∂x

(x, t) dt + f(x, b(x))b

(x).

HINT: G

(x) =

∂F

∂x

(x, b(x)) +

∂F

∂y

(x, b(x))b

(x)

H. Suppose that f ∈ C

[0, 1] such that f

(x) + bf

(x) + cf(x) = 0, f(0) = 0 and

(0) = 1. Let d(x) be continuous on [0, 1] and deﬁne g(x) =

f(x − t)d(t) dt.

Prove that g(0) = g

(0) = 0 and g

(x) + bg

(x) + cg(x) = d(x).

I. Suppose that f

are Riemann integrable integrable functions on [a, b] that converge

uniformly to a function f. Prove that f is Riemann integrable.

HINT: Use Lebesgue’s Theorem (Theorem 6.6.6).

8.4. Series of Functions

By analogy with series of numbers, we deﬁne a series of functions,

∞

n=1

(x),

as the limit of the sequence of partial sums. Thus, we say

∞

n=1

(x) converges

pointwise (or uniformly) if the partial sums

n=1

(x) converge pointwise (or uni-

formly).

8.4.1. EXAMPLE. Consider the series of functions

∞

n=1

sin(nx)

. To see that the

partial sums converge, ﬁrst observe that if k ≥ l, then

n=1

(x) −

n=1

(x)

≤

n=l+1

(x)| ≤

n=l+1

226 Limits of Functions

∞

n=1

is a convergent series, the Cauchy criterion shows that for any ε > 0,

there is an integer N so that if l, k ≥ N, then

n=l+1

< ε. Thus, for l, k ≥ N,

n=1

(x) −

n=1

(x)

< ε,

proving that the partial sums are uniformly Cauchy and so converge.

8.4.2. EXAMPLE. On the other hand, consider the sequence of functions f

[0, 1] given by f

(0,1/n)

. For any x in [1/(n + 1), 1/n), the values f

n+1

(x),

n+2

(x), . . . are all zero and the values f

(x), . . . , f

(x) are all one. Hence

∞

k=0

(x) = n for

n + 1

≤ x <

Thus, the series

∞

n=1

converges at each point of [0, 1]. It does not converge uni-

formly, since for all k > l, we have

n=1

(x) −

n=1

(x)

≥ f

l+1

(x) = 1 for all x ∈ (0, 1/(l + 1)).

8.4.3. EXAMPLE. One of the most important types of series of functions is a

power series. This is a series of the form

∞

n=1

= a

+ a

x + a

+ a

+ ··· .

We will consider these series in detail in the next section. As a starter, consider the

series

∞

n=0

. Fixing x ∈ R, we can apply the Ratio Test, to obtain

lim

n→∞

n+1

/(n + 1)!

/n!

= lim

n→∞

n + 1

= 0.

So this series converges pointwise for each x ∈ R. After ﬁrst obtaining a few

theorems, we will see that it converges uniformly on each interval [−A, A]. We

evaluate it in Example 8.5.4.

Using the partial sums, we can translate all of the results of the previous sec-

tion about sequences of functions into results about series of functions. Here are

two samples. We leave the reformulation of the other theorems of Section 8.2 as

exercises.

8.4 Series of Functions 227

8.4.4. THEOREM. Let (f

) be a sequence of continuous functions from a subset

S of R

into R

. If

∞

n=1

(x) converges uniformly, then it is continuous.

8.4.5. DEFINITION. Let S ⊂ R

. We say that a series of functions f

from S

to R

is uniformly Cauchy on S if for every ε > 0, there is an N so that

i=k+1

(x)

≤ ε whenever x ∈ S and l > k ≥ N.

The proof that a series of real numbers converges if and only if it is Cauchy can

be modiﬁed in a straightforward way to show the following.

8.4.6. THEOREM. A series of functions converges uniformly if and only if it is

uniformly Cauchy.

PROOF. Let f

be the nth partial sum. If f

converges uniformly to f, then for

each ε > 0, there is N ∈ N so that kf

− fk < ε/2 for all n ≥ N. If m, n ≥ N,

− f

k ≤ kf

− fk + kf − f

k <

= ε.

Conversely, if (f

) is uniformly Cauchy, then (f

(x)) is Cauchy for every x, and

thus f(x) = lim

n→∞

(x) exists as a pointwise limit. Moreover, if ε > 0 and

− f

k < ε for all m, n ≥ N, then

kf − f

k = lim

m→∞

− f

k ≤ ε.

Thus this convergence is uniform. ¥

There is a useful test for uniform convergence of a series of functions. The

proof is easy, and the test comes up often in practice.

8.4.7. WEIERSTRASS M-TEST.

Suppose that a

(x) is a sequence of functions on S ⊂ R

into R

and (M

) is a

sequence of real numbers so that

∞

= sup

x∈S

(x)k ≤ M

for all x ∈ S.

∞

n=1

converges, then the series

∞

n=1

(x) converges uniformly on S.

PROOF. For each x ∈ S, the sequence (a

(x)) is an absolutely convergent se-

quence of real numbers since

∞

n=1

(x)k <

∞

n=1

∞

≤

∞

n=1

< ∞.

228 Limits of Functions

Thus the sum exists. Deﬁne f(x) =

∞

n=1

(x). Then for every x ∈ S,

f(x) −

n=1

(x)

∞

n=k+1

(x)

≤

∞

n=k+1

(x)k

≤

∞

n=k+1

∞

≤

∞

n=k+1

This estimate does not depend on x. Thus

lim

k→∞

f −

n=1

∞

≤ lim

k→∞

∞

n=k+1

= 0.

Therefore, this series converges uniformly to f . ¥

As an application, we return to the series

∞

n=0

considered in Example 8.4.3.

On any interval [−A, A] with A ≥ 0, |x

/n!| ≤ A

/n! =: M

. Applying the

Ratio Test to M

shows that

∞

n=0

converges. Hence by the M-test, the series

converges uniformly on [−A, A]. The series does not converge uniformly on the

whole real line, but since it converges uniformly on every bounded interval, we

may conclude that the limit is continuous on the whole line.

8.4.8. EXAMPLE. Consider the geometric series

∞

n=0

(−x

)

. The ratio of suc-

cessive terms this series at the point x is −x

. Thus for |x| < 1, this series con-

verges; while it diverges for |x| > 1. By inspection, it also diverges at x = ±1. For

each x in (−1, 1), we readily obtain that

∞

n=0

(−x

)

1 − (−x

)

1 + x

On the interval of convergence (−1, 1), the convergenceis not uniform. Indeed,

for any integer N, take a = 2

−1/2N

and note that the Nth term (−a

)

large. However, on the interval [−r, r] for any r < 1, we have

sup

|x|≤r

|(−x

)

| = r

Since

∞

n=0

1 − r

< ∞, the Weierstrass M-test shows that the series con-

verges uniformly to f(x) =

1 + x

on [−r, r].

8.4 Series of Functions 229

Consider the functions

(x) :=

k=0

(−t

)

dt =

k=0

(−1)

2k + 1

2k+1

Apply Theorem 8.3.1 to see that the F

converge uniformly on [−r, r] to the func-

tion

F (x) =

1 + t

dt = tan

−1

(x).

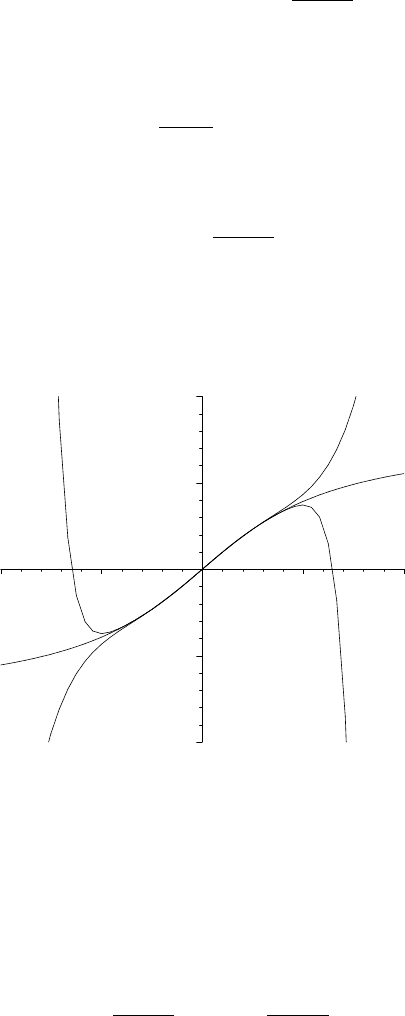
This yields the Taylor series for tan

−1

about the point 0. (See Section 10.1.)

tan

−1

(x) =

∞

n=0

(−1)

2n + 1

2n+1

The radius of convergence of this series is still 1.

This converges at x = ±1 as well because it is an alternating series in which

the terms are monotone decreasing to zero.

–2

–1

–2

–1 1

FIGURE 8.4. The function tan

−1

with the degree 5 and 11 approximations.

It happens that this convergence is uniform on the whole interval [−1, 1]. To

see this, we need the error estimate for alternating series that shows that the size

of the next term is a bound on the error, Corollary 3.2.7. Note that the series is an

alternating series for every x ∈ R. The terms converge monotonely to 0 precisely

when |x| ≤ 1. So the error between the nth partial sum and the limit is no greater

than

sup

|x|≤1

(−1)

2n + 1

2n+1

≤

2n + 1

Since this tends to 0, the series converges uniformly on [−1, 1] to tan

−1

(x).

230 Limits of Functions

8.4.9. EXAMPLE. The reason we have not proved good results about the deriv-

ative of uniformly convergent sequences is that, in general, there is nothing good

to say. Indeed, there are continuous functions that are not differentiable at any

point. These are called nowhere differentiable functions. The ﬁrst example was

constructed by Bolzano sometime before 1830 but was not published. Weierstrass

independently discovered such functions in 1861 and he published his construction

in 1872.

To construct a continuous nowhere differentiable function, let

f(x) =

k≥1

−k

cos(10

πx).

Set f

(x) = 2

−k

cos(10

πx). Then

k≥1

∞

k≥1

−k

= 1 converges.

Thus by the Weierstrass M-test, this series converges uniformly on the whole real

line to a continuous function.

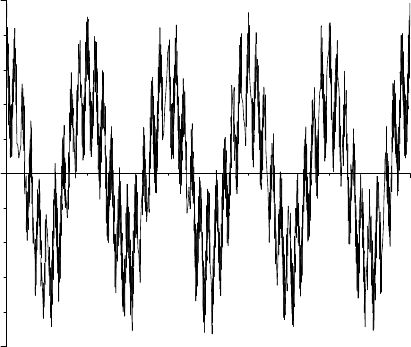
Figure 8.5 gives the graph of a partial sum

k=1

−k

cos(10

πx). Bear in mind

that such a function, being a ﬁnite linear combination of inﬁnitely differentiable

functions, is inﬁnitely differentiable. The limit, however, is not even once differen-

tiable.

–1

FIGURE 8.5. An approximant to Weierstrass’s function.

Consider an arbitrary point x in R, say x = x

. . . . We will show that

f is not differentiable at x by constructing a sequence z

converging to x so that

the difference quotient |f (z

) − f (x)|/|z

− x| goes to +∞.

Fix n ≥ 1. Let y

= x

. . . x

and y

= y

+ 10

−n

. So y

≤ x ≤ y

. Let

us estimate |f(y

) − f(y

)|. As 10

πy

and 10

πy

are integer multiples of π, we

have

) = (−1)

−n

and f

) = (−1)

−n

8.4 Series of Functions 231

Hence |f

) − f

)| = 2

1−n

. For k > n, 10

π is an integer multiple of 2π.

So f

) = f

) = 2

−k

. And for 1 ≤ k < n, the Mean Value Theorem yields

) − f

)| ≤ kf

∞

− y

| = (2

−k

π)10

−n

= 2

−n

π5

k−n

Combining all of these estimates judiciously, we obtain

|f(y

) − f (y

)| ≥ |f

) − f

)| −

k6=n

) − f

≥ 2

1−n

−

n−1

k=1

−n

π5

k−n

> 2

−n

2 −

> 2

−n

One of these values is far from f(x) since

|f(y

) − f (x)|+ |f(x) − f(y

)| ≥ |f (y

) − f(y

)| > 2

−n

Choose i = 0 or 1 so that |f (y

) − f(x)| > 2

−n−1

, and set z

= y

. Clearly

− x| ≤ |y

− y

| = 10

−n

. Therefore,

f(z

) − f (x)

− x

≥

−n−1

−n

= 5

/2.

As n tends to inﬁnity, it is clear that the sequence (z

) converges to x while the

differential quotient blows up. Therefore, f is not differentiable at x.

Exercises for Section 8.4

A. Reformulate Theorem 8.3.1 and Corollary 8.3.2 in terms of series of functions.

B. Prove Theorem 8.4.6.

C. (a) Show that

∞

n=1

−nx

converges uniformly on [0, A] for each A > 0.

(b) Does it converge uniformly on [0, ∞) ?

D. Does

∞

n=1

+ n

converge uniformly on the whole real line?

E. Show that if

∞

n=1

| < ∞, then

∞

n=1

cosnx converges uniformly on R.

F. (a) Let f

(x) =

(1 + x

)

for x ∈ R. Evaluate the sum S(x) =

∞

n=0

(x).

(b) Is this convergence uniform? For which values a < b does this series converge

uniformly on [a, b]?

G. Consider the series

∞

n=0

x − 7

x + 1

for x 6= −1. Find the limit, and discuss where the

convergence is uniform or not.

H. Suppose that a

(x) are continuous functions on [0, 1], and deﬁne s

(x) =

k=1

(x).

Show that if (s

) converges uniformly on [0, 1], then (a

) converges uniformly to 0.

232 Limits of Functions

I. Prove the series version of Dini’s Theorem (Exercise 8.1.I): If g

are nonnegative

continuous functions on [a, b] and

∞

n=1

converges pointwise to a continuous function

on [a, b], then it converges uniformly.

J. Let (f

) be a sequence of functions deﬁned on N such that lim

k→∞

(k) = L

exists

for each n ≥ 0. Suppose that kf

∞

≤ M

where

∞

n=0

< ∞. Deﬁne a function

F (k) =

∞

n=0

(k). Prove that lim

k→∞

F (k) =

∞

n=0

HINT: Think of f

as a function g

on {

: k ≥ 1}∪{0}. How will you deﬁne g

(0)?

K. Apply the previoustheorem to the functions f

(k) =

for n ≥ 0 and k ≥ 1.

Hence show that lim

k→∞

1 +

= e

L. In Example 8.4.9, we could use f (x) =

k≥1

cos(a

πx), where b < 1 and a is an

even integer. Prove that if ab > 1 + π/2, then f is nowhere differentiable.

M. Let d(x) = dist(x, N) and f

(x) = 2

−k

d(2

x) − 2d(2

k−1

for k ≥ 1.

(a) Compute g

(x) = d(x) +

k=1

(x).

(b) Where does g

fail to be differentiable? This is an increasing sequence of sets with

union dense in R.

. How can it turn out to be differentiable?

8.5. Power Series

As mentioned in the previous section, a power series is a series of functions of

the form

∞

n=0

= a

+ a

x + a

+ a

+ ··· .

Formally, this is a power series in x and we could also consider a power series in

x − x

, namely

∞

n=0

(x − x

)

= a

+ a

(x − x

) + a

(x − x

)

+ a

(x − x

)

+ ··· .

This increase in generality is only apparent, as we can set y = x − x

and work

with a power series in y.

Clearly, a power series converges when x = 0. This may be the only value of x

for which the series converges. For example, apply the Ratio Test to

∞

n=1

n!x

. The

following theorem provides a full answer to the general question of when a power

series converges.