Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

5.1 Limits and Continuity 113

C. Show that the sawtooth function

f(x) =

(

x − 2n if 2n ≤ x ≤ 2n + 1, n ∈ Z

2n − x if 2n − 1 ≤ x ≤ 2n, n ∈ Z

is continuous.

D. Consider a function deﬁned on R

f(x, y) =

(

(1 + xy)

1/x

if x 6= 0

if x = 0.

Prove carefully that f is continuous at (0, y

E. Consider a function deﬁned on R

f(x, y) =

(

0 if y ≤ 0 or if y ≥ x

sin

πy

if 0 < y < x

(a) Show that f is not continuous at the origin.

(b) Show that the restriction of f to any straight line through the origin is continuous.

F. (a) Show that the deﬁnition of limit can be reformulated using open balls instead of

norms as follows: A function f mapping a subset S ⊂ R

into R

has limit v

as x approaches a provided that for every ε > 0, there is an r > 0 such that

(a) ∩ S \ {a}

⊂ B

(v).

(b) Provide a similar reformulation of the statement that f is continuous at a.

G. Suppose that functions f, g, h mapping S ⊂ R

into R satisfy f(x) ≤ g(x) ≤ h(x)

for x ∈ S. Suppose that c is a limit point of S and

lim

x→c

f(x) = lim

x→c

h(x) = L.

Show that lim

x→c

g(x) = L.

H. Deﬁne a function on the set S = {0} ∪ {

: n ≥ 1} by f (

) = a

and f(0) = L.

Prove that f is continuous on S if and only if lim

n→∞

= L.

I. Show that if f : [a, b] → R is a differentiable function such that |f

(x)| ≤ M on [a, b],

then f is Lipschitz. HINT: Mean Value Theorem.

J. Find a bounded continuous function on R that is not Lipschitz.

HINT: The derivative should blow up somewhere.

K. (a) Show that a linear transformation A : R

→ R

with m × n matrix

can be

written as A =

i=1

j=1

(b) Show that ²

is Lipschitz with constant 1.

i=1

j=1

NOTE: This estimate is weaker than the one obtained in Corollary 5.1.7 but does

not require the Schwarz inequality.

114 Functions

L. Consider the linear transformation on R

given by the matrix

A =







−







(a) Compute the Lipschitz constant obtained in Corollary 5.1.7.

(b) Show that kAxk = kxk for all x ∈ R

. Hence deduce that the optimal Lipschitz

constant is 1. HINT: The columns of A form an orthonormal basis for R

M. At some point, you may have been told that a continuous function is one that can be

drawn without lifting your pencil off the paper. Is this actually true?

5.2. Discontinuous Functions

The purpose of this section is to show, through a variety of examples, some

of the pathologies that can occur in discontinuous functions. We make no serious

attempt to classify discontinuities, although we give names to some of the simpler

kinds, the ones that have useful descriptions.

5.2.1. EXAMPLE. Consider

f(x) =

(

0 if x 6= 0

1 if x = 0.

This function is discontinuous at 0 because

lim

x→0

f(x) = 0 6= 1 = f(0).

This is the simplest kind of discontinuity, known as a removable singularity be-

cause the function may be altered at the point of discontinuity in order to ﬁx the

problem. Changing f(0) to 0 makes the function continuous.

5.2.2. EXAMPLE. For our next example of a discontinuous function, consider

the Heaviside function, which is much used in engineering. Its graph is given in

Figure 5.3. Deﬁne H on R by

H(x) =

(

0 if x < 0

1 if x ≥ 0.

We claim that lim

x→0

H(x) does not exist. Suppose lim

x→0

H(x) = L, for some

number L. Then for any ε > 0, there would be some r > 0 so that

|H(x) − L| < ε whenever 0 < |x − 0| < r.

Let ε = 1/2 and let r be any positive real number. The values ±r/2 both satisfy

| ± r/2 −0| = r/2 < r. But for any choice of L, the triangle inequality yields

) − L

−r

) − L

≥

) − H(

−r

)

= 1.

5.2 Discontinuous Functions 115

FIGURE 5.3. The Heaviside function.

Therefore, we conclude that

max

) − L

−r

) − L

≥

= ε.

So no possible limit can exist. This trick has the effect of removing consideration

of what the limit L might be and eliminates all possible limit values at the same

time.

However, H is continuous at every a 6= 0. Indeed, if |x − a| < |a|, then a and

x have the same sign. Hence

|H(x) − H(a)| = 0 < ε

for any ε > 0.

There is no way to “repair” this discontinuity by redeﬁning H at the origin.

However, it is not difﬁcult to understand this function’s behaviour. We make the

following deﬁnition of one-sided limits.

5.2.3. DEFINITION. Say that the limit of f as x approaches a from the right is

L if for every ε > 0, there is an r > 0 so that

|f(x) − L| < ε for all a < x < a + r.

We write lim

x→a

f(x) = L.

Similarly, we deﬁne a limit from the left, and write lim

x→a

−

f(x) = L.

5.2.4. DEFINITION. When a function f on R has limits from the left and right

that are different, we say that f has a jump discontinuity. A function on an interval

is called piecewise continuous if on every ﬁnite subinterval, it has only a ﬁnite

number of jump discontinuities and is continuous at all other points.

Indeed, the restriction of H to [0, ∞) is constant and therefore continuous.

What happens at a = 0 is that

lim

x→0

H(x) = 1 = H(0).

Also on (−∞, 0) the function is continuous and moreover has a limit at 0. That is,

lim

x→0

−

H(x) = 0.

Thus H is a piecewise continuous function with a jump discontinuity at 0.

116 Functions

Piecewise continuity allows a function to have inﬁnitely many jump disconti-

nuities, provided the set of jump discontinuities does not “bunch up.” For example,

the ceiling function on R, deﬁned by letting dxe be the least integer greater than

or equal to x, is piecewise continuous on R.

We also consider what it means to have an inﬁnite limit.

5.2.5. DEFINITION. Say that the limit of a function f(x) as x approaches a is

+∞ if for every positive integer N , there is an r > 0 so that

f(x) > N for all 0 < |x − a| < r.

We write lim

x→a

f(x) = +∞. We deﬁne the limit lim

x→a

f(x) = −∞ similarly.

5.2.6. EXAMPLE. Another simple type of discontinuity was already observed

in Example 5.1.3. Deﬁne f on R

f(x) =

(

1/kxk if x 6= 0

0 if x = 0.

This was shown to be continuous on R

\ {0}. However,

lim

x→0

f(x) = +∞.

Indeed, for each positive integer N, take r = 1/N. Then for 0 < kxk < 1/N , we

have f(x) > N as desired.

No redeﬁnition of the value of f at the origin can make this function continu-

ous. Nevertheless, this can be seen as a straightforward kind of behaviour.

Let us look at two examples that behave more wildly.

5.2.7. EXAMPLE. Consider the function deﬁned on R

f(x, y) =







+ y

if (x, y) 6= (0, 0)

0 if (x, y) = (0, 0).

It is easy to verify that f is continuous on R

\ {(0, 0)}. However, at the origin,

this function behaves in a nasty fashion. To understand this function, we convert to

polar coordinates.

Recall that a vector (x, y) 6= (0, 0) is determined by its length r =

+ y

and the angle θ that the vector makes to the positive real axis determined up to a

multiple of 2π by

x = r cos θ and y = r sinθ.

With this notation, we may compute

f(x, y) =

+ y

cos

= cos

θ.

5.2 Discontinuous Functions 117

Now it is clear that this function is constant on rays from the origin (those points

with a ﬁxed angle in polar coordinates). However, eventhough the function remains

bounded, its value, f(x, y), oscillates between 0 and 1 as (x, y) progresses around

the circle. There is no limit as one approaches the origin from an arbitrary direction

as every value in [0, 1] is a limit value of some sequence.

5.2.8. EXAMPLE. A similar phenomenon can be seen in functions on the real

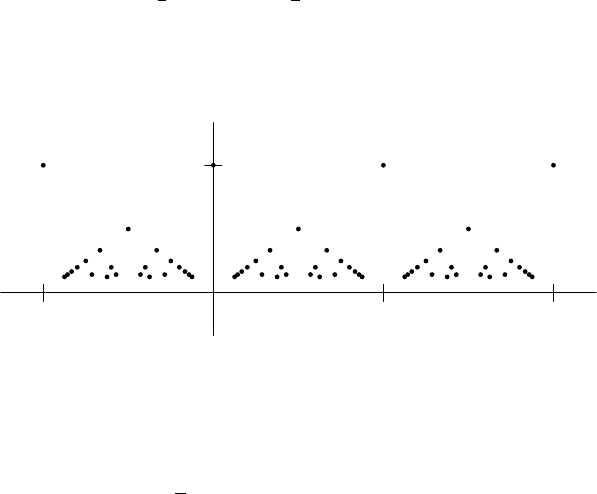
line. Consider the function graphed in Figure 5.4, which is given by

f(x) =

(

sin

if x 6= 0

0 if x = 0.

First think about the problem of graphing this function. Evidently, f(−x) = −f(x)

so it sufﬁces to consider x > 0 and reﬂect to the left half line using the fact that this

is an odd function. Now as x tends to +∞, the reciprocal 1/x tends monotonically

to zero. As sinθ ≈ θ for small values of θ, our function is asymptotic to the curve

y = 1/x as x tends to +∞, meaning lim

x→∞

|f(x) − 1/x| = 0.

FIGURE 5.4. A partial graph of sin(1/x).

On the other hand, as x tends to 0

, 1/x goes off to +∞. Indeed, it passes

through values from 2nπ to 2(n + 1)π as x passes from

2nπ

2(n+1)π

. Hence sin

takes values running from 0 up to 1, down to −1, and back up to 0. This happens

inﬁnitely often as x approaches the origin. So the curve oscillates rapidly up and

down between 1 and −1. No limit is possible.

General arguments show that this function is continuous on R \{0}. However,

it has a nasty discontinuity at 0. Let us show that every value in [−1, 1] is a limit

value along some subsequence. Consider a number t = sinθ. Notice that

f(x) = t if and only if sin

= sin θ

if and only if

= θ + 2nπ or (π − θ) + 2nπ, n ∈ Z

if and only if x =

θ+2nπ

(π−θ)+2nπ

, n ∈ Z.

In particular,

lim

n→∞

θ+2nπ

) = sin θ = t.

118 Functions

This shows that every point (0, t) for |t| ≤ 1 lies in the closure of the graph of f.

It is not difﬁcult to see that the closure of the graph is precisely this line segment

together with the graph itself.

Finally, we look at a couple of bizarre examples.

5.2.9. EXAMPLE. For any subset A of R

, the characteristic function of A is

(x) =

(

1 if x ∈ A

0 if x /∈ A.

The behaviour of this function depends on the character of the set A. See Exer-

cises 5.2.A.

Let us take A to be the set Q of rationals in R. The function

takes the values

0 and 1 on every open interval, no matter how small, because the sets of the rational

and the irrational numbers are both dense in the line. Thus for every a ∈ R and

any r > 0 there is a point x with |x − a| < r such that |f(x) − f(a)| = 1. (Just

take x irrational if a is rational and x rational if a is irrational.) This function is not

continuous at any point!

5.2.10. EXAMPLE. This last example is perhaps the strangest of all. Let

f(x) =

(

0 if x /∈ Q

if x =

in lowest terms and q > 0

meaning that p, q are integers with no common factor. Figure 5.5 shows part of

the graph of this function. We will show that this function is continuous at every

irrational point, and discontinuous at every rational point.

−1

1 2

FIGURE 5.5. Partial graph of function f(p/q) = 1/q.

First suppose that a is irrational and ε > 0. Fix an integer M > |a|. There is

an integer N sufﬁciently large that 1/N < ε. The set

S =

: 1 ≤ q ≤ N, −Mq ≤ p ≤ Mq

is ﬁnite and thus is closed. Since S does not contain the point a and its complement

is open, there is a real number r > 0 such that the ball B

(a) is contained in

5.2 Discontinuous Functions 119

∩ (−M, M), and so is disjoint from S. Now if x ∈ (−M, M) is not in S, then

either it is irrational, whence f (x) = 0, or it is a rational

with q > N, whence

f(x) <

< ε. Hence

|f(x) − f(a)| = |f(x)| < ε for all |x − a| < r.

This shows that f is continuous at each irrational point.

Now consider a rational a =

in lowest terms. Then f(a) =

> 0. Take

ε =

. For every r > 0, there are irrational numbers x with |x − a| < r. Thus

|f(x) − f(a)| =

6< ε.

Consequently, f is not continuous at a.

In fact, f does have a limit at a and so the discontiniuity at a is removable.

Deﬁning the set S as in the irrational case, there is a real number r > 0 such that

(a) \ {a} is disjoint from the set S. Hence we conclude that

|f(x)| < ε for all 0 < |x − a| < r.

Therefore, lim

x→a

f(x) = 0 for every point a in R. Since f(a) 6= 0 when a is rational,

this shows by another method that f is discontinuous there. The really amazing

fact is that f has a limit at every point in R yet is discontinuous on a dense set.

Exercises for Section 5.2

A. Let A be a subset of R

. Show that the characteristic function

is continuous on

the interior of A and on the interior of its complement A

but is discontinuous on the

boundary ∂A =

A ∩ A

B. Show that f(x) = x log x

for x ∈ R \ {0} has a removable singularity at x = 0.

C. Give an example of a bounded function f : [−1, 1] → R that has only jump disconti-

nuities but is not piecewise continuous.

D. What is the nature of the singularity at x = 1 of the function f(x) = x

1−x

deﬁned for

x ≥ 0, x 6= 1? HINT: lim

x→1

log x

x−1

is a derivative.

E. Let f(x) = sin

−1

(sinx), where sin

−1

(y) is the unique value θ ∈ [−

] such that

sinθ = y.

(a) Show that f

has left and right limits at every point.

(b) Where is f

discontinuous?

F. Prove that L = lim

x→a

f(x) if and only if both lim

x→a−

f(x) = L and lim

x→a+

f(x) = L.

G. (A monotone convergence test for functions.) Suppose that f is an increasing function

on (a, b) that is bounded above. Prove that the one-sided limit lim

x→b−

f(x) exists.

H. Deﬁne f on R by f(x) = x

(x). Show that f is continuous at 0 and that this is the

only point where f is continuous.

120 Functions

5.3. Properties of Continuous Functions

We start with several properties equivalent to continuity. Then we will record

various consequences of continuity, most of which are easy to verify. As the do-

main of a function is often a proper subset of R

, we introduce another topological

notion. A subset V ⊂ S ⊂ R

is open in S or relatively open (with respect to S)

if there is an open set U in R

such that U ∩ S = V . In other words, V is open in

S if for every v ∈ V , there is an ε > 0 so that B

(v) ∩ S ⊂ V .

5.3.1. THEOREM. For a function f mapping S ⊂ R

into R

, the following

are equivalent:

(1) f is continuous on S.

(2) For every convergent sequence (x

)

∞

n=1

with lim

n→∞

= a in S,

lim

n→∞

f(x

) = f (a).

(3) For every open set U in R

, the set

−1

(U) = {x ∈ S : f(x) ∈ U}

is open in S.

PROOF. If we assume (1), that is, f is continuous on S, then clearly (2) holds.

Conversely, assume that (1) is false, and f is not continuous at some point a ∈ S.

Then reversing the deﬁnition of continuity, we can ﬁnd some positive number ε > 0

for which the deﬁnition fails, meaning that there is no value of r > 0 that works.

That is, ﬁxing this ε, for every r > 0 there is some point x ∈ S (depending on r)

such that

kx − ak < r and kf(x) − f(a)k ≥ ε.

So take r = 1/n and ﬁnd an x

∈ S with

− ak <

and kf(x

) − f (a)k ≥ ε.

It follows that lim

n→∞

= a and f(x

) does not converge to f(a). This shows that

if (1) fails, then (2) is false also. Therefore, (1) and (2) are equivalent.

Suppose that f is continuous and U is an open subset of R

. Pick any point

a in f

−1

(U). Since U is open and contains u = f(a), there is an ε > 0 such that

(u) is contained in U. From the continuity of f, there is a real number r > 0

such that

kf(x) − uk < ε for all x ∈ S, kx − ak < r.

This means that f

(a)∩S

is contained in B

(u) and thus in U . Hence f

−1

(U)

contains B

(a) ∩ S. Consequently, f

−1

(U) is open in S.

Conversely, suppose that (3) holds. Fix a in S and ε > 0. Using the open set

U = B

(f(a)), we obtain an open set f

−1

(U) in S containing a. Therefore, there

is a real number r > 0 such that

(a) ∩ S ⊂ f

−1

(U).

5.3 Properties of Continuous Functions 121

In other words, kf(x) − f(a)k < ε for all x ∈ S such that kx − ak < r. So f is

continuous. ¥

Property (2) could be called the sequential characterization of continuity.

It will often be more convenient to work with a sequence and this property rather

than ﬁnding some r for each ε, as in the original deﬁnition. Property (3) could be

called the topological charactizeration of continuity. This is a formulation that

readily generalizes to settings in which there is no appropriate distance function. In

certain ways, this version is more powerful than the others, but it is only valid for

continuity on a set, not continuity at a point.

Recall that if f, g are functions from a common domain S ⊂ R

into R

and

α, β ∈ R, then αf +βg denotes the function that sends x to αf(x)+ βg(x). When

the range is R, f g denotes the function sending x to f(x)g(x). From the properties

of limits and the deﬁnition of continuity, we obtain the following basic properties.

5.3.2. THEOREM. If f, g are functions from a common domain S into R

and

a ∈ S such that lim

x→a

f(x) = u and lim

x→a

g(x) = v, then

(1) lim

x→a

f(x) + g(x) = u + v,

(2) lim

x→a

αf(x) = αu for any α ∈ R.

When the range is contained in R, say lim

x→a

f(x) = u and lim

x→a

g(x) = v, then

(3) lim

x→a

f(x)g(x) = uv, and

(4) lim

x→a

f(x)

g(x)

provided that v 6= 0.

PROOF. The proofs are analogous to the corresponding fact for limits of sequences.

We will prove (1) from the deﬁnition of limit. The others will be left as exercises.

Let ε > 0 be given. From lim

x→a

f(x) = u and using ε/2 in the deﬁnition of

limit, there is an r

> 0 such that

kf(x) − uk <

for all x ∈ S with kx − ak < r

Similarly, for lim

x→a

g(x) = v, there is an r

> 0 such that

kg(x) − vk <

for all x ∈ S with kx − ak < r

Take r = min{r

, r

}, which is positive. Then for kx − ak < r,

k(f + g)(x) − (u + v)k = k(f(x) − u) + (g(x) − v)k

≤ k(f (x) − u)k + k(g(x) − v)k

= ε.

This establishes that lim

x→a

f(x) + g(x) = u + v. ¥

122 Functions

5.3.3. THEOREM. If f, g are functions from a common domain S into R

that

are continuous at a ∈ S, and α ∈ R, then

(1) f + g is continuous at a,

(2) αf is continuous at a,

and when the range is contained in R,

(3) fg is continuous at a, and

(4) f/g is continuous at a provided that g(a) 6= 0.

PROOF. We prove (3) and leave the others as exercises. To show that fg is contin-

uous at a, we must show that lim

x→a

fg(x) = f(a)g(a). By Theorem 5.3.2 (3),

lim

x→a

fg(x) = lim

x→a

f(x)g(x) = lim

x→a

f(x) lim

x→a

g(x) = f(a)g(a),

where the last equality follows from f and g each being continuous. ¥

5.3.4. EXAMPLE. Observe that the function f(x) = x is continuous at every

a ∈ R, since lim

x→a

f(x) = lim

x→a

x = a. By Theorem 5.3.3 (2), products of this

function are continuous, so g(x) = x

, h(x) = x

, and in general k(x) = x

for

every positive integer n are all continuous functions. By Theorem 5.3.3 (1) and

(3), linear combinations of these functions are continuous, and so we conclude that

every polynomial is continuous on R.

If f is a rational function—that is, f(x) = p(x)/q(x), where p and q are

polynomials—then f is continuous at all a ∈ R, where q(a) 6= 0. This follows

from the previous paragraph and Theorem 5.3.3 (4).

Recall that if f maps a domain S ⊂ R

into a set T ⊂ R

, and g maps T into

, then the composition of g and f, denoted g ◦ f, is the function that sends x to

g(f(x)). For example, if f(x, y) = x

+ y

is deﬁned on R

and g(x) =

√

x for

x ∈ [0, ∞), then g ◦ f (x, y) =

+ y

5.3.5. THEOREM. Suppose that f maps a domain S contained in R

into a

subset T of R

, and g maps T into R

. If f is continuous at a ∈ S and g is

continuous at f(a) ∈ T , then the function g ◦f is continuous at a. Thus if f and g

are continuous, then so is g ◦ f.

PROOF. We will use the sequential characterization of continuity. Let (x

)

∞

n=1

any sequence of points in S with lim

n→∞

= a. Since f is continuous at a, we

know that lim

n→∞

f(x

) = f(a). Thus (f(x

))

∞

n=1

is a sequence in T with limit

f(a), and since g is continuous at f (a), we conclude that

lim

n→∞

g(f(x

)) = g(f(a)).

Therefore, by Theorem 5.3.1, g ◦ f is continuous at a. ¥