Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

4.2 Convergence and Completeness in R

4.2.2. LEMMA. Let (x

) be a sequence in R

. Then lim

k→∞

= a if and only if

lim

k→∞

− ak = 0.

The second limit is a sequence of real numbers, and thus it may be understood

using only ideas from Chapter 2.

Just as important is the relation between convergence in R

and convergence

of the coefﬁcients. The following lemma is conceptually quite easy (draw a picture

in R

), but the proof requires careful bookkeeping.

4.2.3. LEMMA. A sequence x

= (x

k,1

, . . . , x

k,n

) in R

converges to a point

a = (a

, . . . , a

) if and only if each coefﬁcient converges:

lim

k→∞

k,i

= a

for 1 ≤ i ≤ n.

PROOF. First suppose that lim

k→∞

= a. Then given ε > 0, we obtain an integer

N so that kx

− ak < ε for all k ≥ N. Then for each 1 ≤ i ≤ n and all k ≥ N,

k,i

− a

| ≤

j=1

k,j

− a

1/2

= kx

− ak < ε.

Therefore, lim

k→∞

k,i

= a

for all 1 ≤ i ≤ n.

Conversely, suppose that each coordinate sequence x

k,i

converges to a real

number a

for 1 ≤ i ≤ n. Then given ε > 0, use ε/n in the deﬁnition of limit and

choose N

so large that

k,i

− a

| <

for all k ≥ N

Then using N = max{N

: 1 ≤ i ≤ n}, all n of these inequalities are valid for

k ≥ N. Hence

− ak =

i=1

k,i

− a

1/2

i=1

1/2

< ε.

Therefore, lim

k→∞

= a. ¥

Following the same route as for the line, we will deﬁne Cauchy sequences and

completeness in the higher-dimensional context. For the real line, it was necessary

to build the completeness of R into its construction. However, the completeness for

will be a consequence of the completeness of R.

4.2.4. DEFINITION. A sequence x

in R

is Cauchy if for every ε > 0, there

is an integer N so that

− x

k < ε for all k, l ≥ N.

A set S ⊂ R

is complete if every Cauchy sequence of points in S converges to a

point in S.

94 Topology of R

As in Proposition 2.7.1, it is easy to show that a convergent sequence is Cauchy.

Indeed, suppose that lim

k→∞

= a and ε > 0. Then, using ε/2 in the deﬁnition of

limit, choose an integer N so that kx

− ak < ε/2 for all k ≥ N. Then for all

k, l ≥ N , use the triangle inequality to obtain

− x

k ≤ kx

− ak + ka − x

k <

= ε.

The converse lies deeper and is more important.

4.2.5. COMPLETENESS THEOREM FOR R

Every Cauchy sequence in R

converges. Thus, R

is complete.

PROOF. Let x

be a Cauchy sequence in R

. The proof is accomplished by reduc-

ing the problem to each coordinate. Let us write the elements of the sequence as

= (x

k,1

, . . . , x

k,n

). We will show that the sequences (x

k,i

)

∞

k=1

are Cauchy for

each 1 ≤ i ≤ n. Indeed, if ε > 0, choose N so large that

− x

k < ε for all k, l ≥ N.

Then

k,i

− x

l,i

| ≤ kx

− x

k < ε for all k, l ≥ N.

Thus (x

k,i

)

∞

k=1

are Cauchy for 1 ≤ i ≤ n.

By the completeness of R, Theorem 2.7.4, each of these sequences has a limit,

say

lim

k→∞

k,i

= a

for 1 ≤ i ≤ n.

Deﬁne a vector a ∈ R

by a = (a

, . . . , a

). By Lemma 4.2.3, lim

k→∞

= a and

hence R

is complete. ¥

4.2.6. EXAMPLE. Let v

= (0, 0), and deﬁne a sequence v

= (x

, y

) in R

recursively by

n+1

+ y

+ 1

n+1

− y

+ 1

The ﬁrst few terms are

(0, 0), (

), (1,

), (

), . . . .

To get an idea of what the limit might be (if it exists), look for ﬁxed points of

the map

T (x, y) =

x + y + 1

x − y + 1

In other words, solve the equation T u = u. This is a linear system

x =

x +

y +

y =

x −

y +

Solving, we ﬁnd the solution u = (2, 1).

4.2 Convergence and Completeness in R

This leads us to consider the distance of v

to u.

n+1

− uk

= k(x

n+1

− 2, y

n+1

− 1)k

+ y

− 3

− y

− 1

+ y

− 3)

+ (x

− y

− 1)

+ 2y

− 8x

− 4y

+ 10

− 2)

+ (y

− 1)

− uk

By induction, it follows that

− uk = 2

−n/2

− uk = 2

−n/2

√

Hence lim

n→∞

− uk = 0, which means that lim

n→∞

= (2, 1).

Exercises for Section 4.2

A. (a) If (x

)

∞

n=1

is a sequence in R

with lim

n→∞

= a, show that lim

n→∞

k = kak.

(b) Show by example that the converse is false.

B. Show that if (x

)

∞

n=1

is a sequence in R

such that

n≥1

− x

n+1

k < ∞, then

) is a Cauchy sequence.

C. (a) Give an example of a Cauchy sequence for which the condition of the previous

exercise fails.

(b) However, show that every Cauchy sequence (x

)

∞

n=1

has a subsequence (x

)

∞

i=1

such that

i≥1

− x

i+1

k < ∞.

D. Let x

∈ R

and R > 0. Prove that {x ∈ R

: kx − x

k ≤ R} is complete.

E. Let M be a subspace of R

(a) Let {v

, . . . , v

} be an orthonormal basis for M. Formulate an analogue of

Lemma 4.2.3 for M and prove it.

(b) Prove that M is complete.

F. Let v

= (x

, y

) with 0 < x

< y

. Deﬁne v

n+1

= (x

n+1

, y

n+1

) =

√

for all n ≥ 0.

(a) Show by induction that 0 < x

< x

n+1

< y

n+1

< y

(b) Then estimate y

n+1

− x

n+1

in terms of y

− x

n→∞

= (c, c). This value c is

known as the arithmetic–geometric mean of x

and y

G. Let v

= (x

, y

) = (0, 0), and for n ≥ 0 deﬁne

n+1

= (x

n+1

, y

n+1

) =

+ 2y

+ y

+ 1

(a) Show that x

and y

are increasing sequences that are bounded above.

96 Topology of R

(b) Prove that lim

n→∞

exists, and ﬁnd the limit.

H. Let T =

5/4 −1/4

3/4 1/4

. Set x

= T

(1, 0) for n ≥ 1.

(a) Prove that (x

) converges and ﬁnd the limit y.

(b) Find an explicit N so that kx

− yk <

−100

for all n ≥ N.

HINT: Show by induction that x

3−2

−n

3(1−2

−n

)

4.3. Closed and Open Subsets of R

Two classes of subsets play a crucial role in analysis: the closed sets, which

contain all of their limit points, and the open sets, which contain small balls around

each point. These notions will be made precise in this section. From the point of

view thus far, closed sets seem more natural because they are directly connected

to limiting procedures. Later, however, we shall see that open sets play at least

as important a role when considering continuous functions. They are intimately

related in any case. We develop closed sets ﬁrst.

4.3.1. DEFINITION. A point x is a limit point of a subset A of R

if there is a

sequence (a

)

∞

n=1

with a

∈ A such that x = lim

n→∞

. A set A ⊂ R

is closed if

it contains all of its limit points.

NOTE: Be warned that some other books deﬁne limit point to be a slightly more

complicated concept, which we call a cluster point (see Exercise 4.3.N).

4.3.2. EXAMPLES.

(1) [a, b] = {x ∈ R : a ≤ x ≤ b} is closed.

(2) ∅ and R

are both closed.

(3) [0, +∞) is closed in R.

(4) (0, 1] and (0, 1) are not closed.

(5) {x ∈ R

: kxk ≤ 1} is closed.

(6) {x ∈ R

: kxk < 1} is not closed.

(7) {(x, y) ∈ R

: xy ≥ 1} is closed.

(8) Finite sets are closed.

In the following proposition, I denotes an arbitrary index set. This may be an

inﬁnite set of very large cardinality (such as the real line) or a countably inﬁnite set

(like N) or even a ﬁnite set.

4.3 Closed and Open Subsets of R

4.3.3. PROPOSITION. If A, B ⊂ R

are closed, then A ∪ B is closed.

If {A

: i ∈ I} is a family of closed subsets of R

, then

i∈I

is closed.

PROOF. Suppose that (x

)

∞

n=1

is a sequence in A ∪ B with limit x. Clearly, either

inﬁnitely many of the x

’s belong to A or inﬁnitely many belong to B. Without

loss of generality, we may suppose that A has this property. Hence there is a subse-

quence (x

)

∞

i=1

of (x

)

∞

n=1

such that each x

belongs to A. But this subsequence

has limit x. Since A is closed, we deduce that x belongs to A, and thus belongs to

A ∪ B. So A ∪ B is closed.

Now suppose that (x

)

∞

n=1

is a sequence in

i∈I

with limit x. For each

i ∈ I, the sequence (x

)

∞

n=1

belongs to A

, which is closed. Therefore, the limit x

also belongs to A

. Since this holds for every i ∈ I, it follows that x also belongs

to the intersection. Hence the intersection is closed. ¥

Since a closed set has the very useful property of containing all of its limit

points, it is natural to want to construct closed sets from other, less well-behaved

sets. This is the motivation for the following deﬁnition.

4.3.4. DEFINITION. If A is a subset of R

, the closure of A is the set

A con-

sisting of all limit points of A.

To justify the name, we establish some basic properties of the closure operation.

4.3.5. PROPOSITION. Let A be a subset of R

. Then A is the smallest closed

set containing A. In particular, A = A.

PROOF. First notice that for each a in A, we may consider the sequence x

= a

for all n ≥ 1. This has limit a, and thus A is contained in A.

To show that A is closed, consider a sequence (x

)

∞

n=1

, where each x

belongs

A with limit x = lim

n→∞

. For each n, there is a sequence of points in A

converging to x

. Hence we may choose an element a

∈ A from this sequence

such that kx

− a

k <

. Then

lim

n→∞

= lim

n→∞

+ (a

− x

)

= lim

n→∞

+ lim

n→∞

− x

= x + 0 = x.

Thus x is also a limit of points in A, whence it belongs to

A. So A is closed.

If C is a closed set containing A, then it also contains all limits of sequences in

A and therefore contains A. So A is the smallest closed set containing A.

Now A is the smallest closed set containing A. Since A is already closed,

A = A. ¥

98 Topology of R

4.3.6. DEFINITION. The ball about a in R

of radius r is the set

(a) = {x ∈ R

: kx − ak < r}.

A subset U of R

is open if for every a ∈ U, there is some r = r(a) > 0 so that

the ball B

(a) is contained in U .

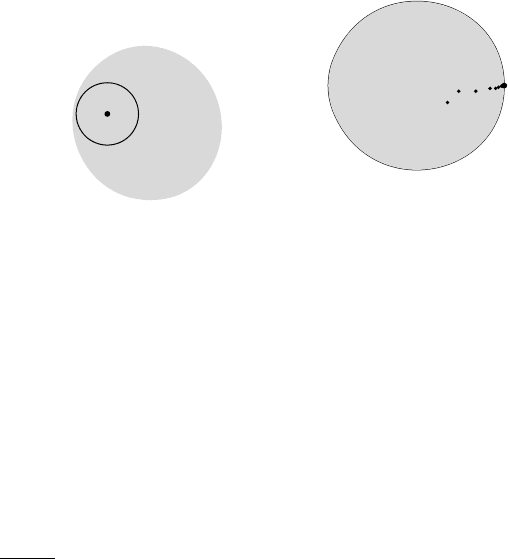
Figure 4.2 illustrates the deﬁnitions of open and closed sets.

lim

k→∞

FIGURE 4.2. Open and closed sets

4.3.7. EXAMPLES.

(1) (a, b) = {x ∈ R : a < x < b} is open.

(2) ∅ and R

are both open.

(3) (0, +∞) is open in R.

(4) (0, 1] and [0, 1] are not open.

(5) B

(a) is open.

(6)

(a) = {x ∈ R

: kx − ak ≤ r} is not open.

(7) {(x, y) ∈ R

: xy < 1} is open.

(8) {(x, 0) ∈ R

: 0 < x < 1} is not open.

It is important to remember that while a door must be either open or closed, a

set can be neither. The following connection between open and closed sets makes

the relation clear.

4.3.8. THEOREM. A set A ⊂ R

is open if and only if the complement of A,

= {x ∈ R

: x /∈ A}, is closed.

PROOF. Let A be open. Let (x

)

∞

n=1

be a sequence in A

with limit x. If a is any

point in A, there is a positive number r > 0 such that B

(a) is contained in A.

4.3 Closed and Open Subsets of R

Hence ka − x

k ≥ r for all n ≥ 1. Therefore,

ka − xk = lim

n→∞

ka − x

k ≥ r.

In particular, x 6= a. This is true for every point in A, and hence x belongs to A

That is, A

is closed.

Conversely, suppose that A is not open. Then there is some a ∈ A so that for

every r > 0, the ball B

(a) is not contained in A. In particular, if we let r =

, we

can ﬁnd x

∈ A

so that ka − x

k <

. Then a = lim

n→∞

is a limit point of A

belonging to A. Hence A

is not closed. ¥

We have the following proposition, which is dual to Proposition 4.3.3. The

proof is left as an exercise.

4.3.9. PROPOSITION. If U and V are open subsets of R

, then U ∩ V is an

open subset of R

. If {U

: i ∈ I} is a family of open subsets of R

, then

i∈I

is open.

There is also a notion for open sets that is dual to the closure. The interior

intX of a set X is the largest open set contained inside X (see the Exercises). If

the interior of a set X is the empty set, then we say X has empty interior.

4.3.10. EXAMPLE. Let A = {(x, y) : x ∈ Q, y > x

}. This set is neither open

nor closed. Indeed, the point (0, 0) = lim

n→∞

(0,

) is a limit point not contained in

A; so A is not closed. And the point (0, 1) = lim

n→∞

(

√

2/n, 1) belongs to A, yet it

is the limit of points in A

. So A is not open either.

The closure of A is the set

A = {(x, y) : y ≥ x

To see this, let (x, y) be given such that y ≥ x

. Let x

be an increasing sequence

of rationals converging to x (such as the ﬁnite decimal approximations of x). Set

= y +

. Then it is clear that y

> x

≥ x

and thus a

= (x

, y

) belongs to

A. Now

lim

n→∞

= x and lim

n→∞

= lim

n→∞

y +

= y.

Hence lim

n→∞

= (x, y). Therefore,

A contains {(x, y) : y ≥ x

}. Conversely, if

(x, y) = lim

n→∞

for any sequence a

= (x

, y

) in A, it follows that

y = lim

n→∞

≥ lim

n→∞

= x

Thus {(x, y) : y ≥ x

} contains A.

In this case, A has empty interior. The reason is that every open ball contains

points with irrational coordinates, and A does not.

The interior of A is the set U = {(x, y) : y > x

}. First we show that U is

open. If a = (x, y) belongs to U, then s = y − x

> 0. We need to determine a

100 Topology of R

value for r so that B

(a) is contained in U. Some calculation is needed to determine

the proper choice. Suppose that a point (u, v) satisﬁes k(u, v) −(x, y)k < r. Then,

in particular, |u − x| < r and |v − y| < r. Hence

v − u

> (y − r) − (x + r)

= y − r − (x

+ 3rx

+ 3r

x + r

)

= y − x

− r − 3rx

− 3r

x − r

= s − (r + 3rx

+ 3r

x + r

To make the right-hand side positive, which we require, a choice must be made for

r so that r + 3rx

+ 3r

x + r

≤ s. Let us decide that r ≤ 1 (our choice—and it

can’t hurt). Then

r + 3rx

+ 3r

x + r

≤ r(2 + 3x

+ 3|x|).

Deﬁne r = min{1, s/(2 + 3x

+ 3|x|)}. Then it follows that

v − u

> s − (r + 3rx

+ 3r

x + r

) > 0.

This shows that B

(a) is contained in U . Thus U is open.

Now suppose that a = (x, y) belongs to

A but is not in U. Then y ≥ x

but

y 6> x

, whence y = x

. To see that a is not in the interior of

A, it must be shown

that whenever r > 0, the ball B

(a) intersects A

. This is easy, since the point

(x, x

− r/2) belongs to this ball and does not belong to A. So intA = U.

Exercises for Section 4.3

A. Find the closure of the following sets:

(a) Q

(b) {(x, y) ∈ R

: xy < 1}

)) : x > 0}

(d) {(x, y) : x, y ∈ Q, x

+ y

< 1}

B. Let (a

)

∞

n=1

be a sequence in R

with lim

n→∞

= a. Show that

A = {a

: n ≥ 1} ∪ {a} is a closed set.

C. Show that U = {(x, y) ∈ R

: x

+ 4y

< 4} is open by explicitly ﬁnding a ball

around each point which is contained in U.

D. If A is a bounded subset of R, show that supA and infA belong to A.

E. Show that the interior satisﬁes intA = (A

)

F. Find the interior of A ∪ B, where A = {(x, y) : x ∈ Q, y

≥ x} and

B = {(x, y) : x /∈ Q, y ≥ x

G. If a subset A of R

has no interior, must it be closed?

H. Show that a subset of R

is complete if and only if it is closed.

I. Prove Proposition 4.3.9 using Theorem 4.3.8 and Proposition 4.3.3.

J. Show that if U is open and A is closed, then U \A = {x ∈ U : x /∈ A} is open. What

can be said about A \ U?

4.4 Compact Sets and the Heine–Borel Theorem 101

K. Suppose that A and B are closed subsets of R.

(a) Show that the product set A × B = {(x, y) ∈ R

: x ∈ A and y ∈ B} is closed.

(b) Likewise show that if both A and B are open, then A × B is open.

L. A set A is dense in B if B is contained in

(a) Show that the set of irrational numbers is dense in R.

(b) Hence show that Q has empty interior.

M. Suppose that A is a dense subset of R

(a) Show that if U is open in R

, then A ∩ U is dense in U .

(b) Show by example that this may fail for sets that are not open.

N. A point x is a cluster point of a subset A of R

if there is a sequence (a

)

∞

n=1

with

∈ A\{x} such that x = lim

n→∞

. Thus, every cluster point is a limit point but not

conversely.

(a) Show that if x is a limit point of A, then either x is a cluster point of A or x ∈ A.

(b) Hence show that a set is closed if it contains all of its cluster points.

O. Starting with a subset A of R

, form all the possible sets that may be obtained by

repeated use of the operations of closure and complement. Up to 14 different sets can

be obtained in this way. Find such a subset of R.

4.4. Compact Sets and the Heine–Borel Theorem

Now we turn to the notion of compactness. At this stage, compactness seems

like a convenience and may not appear to be much more useful than completeness.

However, when we study continuous functions, compactness will be very useful

and then its full power will become apparent.

4.4.1. DEFINITION. A subset A of R

is compact if every sequence (a

)

∞

k=1

of points in A has a convergent subsequence (a

)

∞

i=1

with limit a = lim

i→∞

in A.

Recall that the Bolzano–Weierstrass Theorem (Theorem 2.6.4) states that every

bounded sequence has a convergent subsequence. Using this new language, we

may deduce that every subset of R that is both closed and bounded is compact.

This rephrasing naturally suggests the question, Which subsets of R

are compact?

Before answering this question, we consider a few examples.

4.4.2. EXAMPLES. Consider the set (0, 1]. The sequence 1, 1/2, 1/3, . . . is in

this set but converges to 0, which is not in the set. Since any subsequence will

also converge to zero, there is no subsequence of 1, 1/2, 1/3, . . . that converges to

a number in (0, 1]. So this set is not compact.

Next, consider the set N. The sequence 1, 2, 3, . . . is in N. However, no subse-

quence converges (because each subsequence is unbounded and being bounded is

a necessary condition for convergence by Proposition 2.4.2). So N is not compact.

102 Topology of R

A subset S of R

is called bounded provided that there is a real number R such

that S is contained in the ball B

(0). Equivalently, S is bounded if sup

x∈S

kxk < ∞.

Notice that when n = 1, this deﬁnition of bounded agrees with our old deﬁnition

of bounded subsets of R.

The previous examples suggest that sets that are not closed or not bounded

cannot be compact. This is true, and the proofs are an abstraction of the arguments

for these examples.

4.4.3. LEMMA. A compact subset of R

is closed and bounded.

PROOF. Let C be a compact subset of R

. Suppose that x is a limit point of C,

say x = lim

n→∞

for a sequence (c

) in C. Then this sequence has a subsequence

) converging to a point c in C. Therefore,

x = lim

n→∞

= lim

i→∞

= c ∈ C.

Thus C is closed.

To show that C is bounded, suppose that it were unbounded. That means that

there is a sequence c

∈ C such that kc

k > n for each n ≥ 1. Consider the

sequence (c

). If there were a convergent subsequence (c

) with limit c, it would

follow that

kck = lim

i→∞

k ≥ lim

i→∞

= +∞.

This is an absurd conclusion, and thus C must be bounded. ¥

To establish the converse, we build up a couple of partial results.

4.4.4. LEMMA. If C is a closed subset of a compact subset of R

, then C is

compact.

PROOF. Let K be the compact set containing C. Suppose (x

)

∞

n=1

is a sequence

in C. To show that C is compact, we must ﬁnd a subsequence that converges to an

element of C.

However, (x

)

∞

n=1

is contained in the compact set K. So it has a subsequence

that converges to a number x in K, say x = lim

k→∞

. Since (x

)

∞

k=1

is contained

in C and C is closed, it follows that x belongs to C as required. ¥

4.4.5. LEMMA. The cube [a, b]

is a compact subset of R

PROOF. Let x

= (x

k,1

, . . . , x

k,n

) for k ≥ 1 be a sequence in R

such that

the coefﬁcients satisfy a ≤ x

k,i

≤ b for all k ≥ 1 and 1 ≤ i ≤ n. Consider

the sequence (x

k,1

)

∞

k=1

of ﬁrst coordinates. By the Bolzano–Weierstrass Theorem

(Theorem 2.6.4), there is a subsequence

∞

j=1

converging to a point z

in [a, b],

lim

j→∞

= z