Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

5.3 Properties of Continuous Functions 123

5.3.6. EXAMPLE. If f maps S ⊂ R

into R

, then f

, the ith coordinate of

f(x), is a real-valued function on S. Using this notation, we may write

f(x) = (f

(x), . . . , f

(x)).

We claim that f is continuous if and only if each function f

is continuous for

1 ≤ i ≤ m.

One way to see this is to argue exactly as in Lemma 4.2.3. Instead, we will

use Corollary 5.1.7 and the (continuous) coordinate functions π

: R

→ R and

: R → R

given by

, . . . , x

) = x

and ²

(t) = te

Notice that f

(x) = π

◦ f(x). Thus if f is continuous, each f

is continuous.

Conversely,

f(x) =

i=1

◦ f

(x).

Hence if each f

is continuous, then each ²

◦ f

is continuous by Theorem 5.3.5;

and their sum is continuous by Theorem 5.3.3 (1).

Exercises for Section 5.3

A. Show that the function deﬁned on R

\ {(0, 0)} by f(x, y) =

sin(log(x

+ y

))

cos

y + y

continuous.

B. Use Lemma 4.2.3 and the sequential characterization of continuity to give a second

proof for Example 5.3.6.

C. Consider f mapping S ⊂ R

into R

and two points: a a limit point of S and

v ∈ R

. Show that lim

x→a

f(x) = v if and only if for each sequence (x

) ∈ S\{a}

with lim

n→∞

= a, we have lim

n→∞

f(x

) = v.

D. Suppose that f mapping S ⊂ R

into R

is given by f(x) = (f

(x), . . . , f

(x))

with f

: S → R for each i. Show that lim

x→a

f(x) = (u

, . . . , u

) if and only if

lim

x→a

(x) = u

for each i. HINT: Use the previous exercise and Lemma 4.2.3.

E. Let f and g be continuous mapping of S ⊂ R

into R

. Show that the inner product

h(x) = hf(x), g(x)i is continuous.

F. Finish the proof of Theorem 5.3.2.

G. Suppose that f is a continuous function on [a, b] and g is a continuous function on [b, c]

such that f(b) = g(b). Show that

h(x) =

(

f(x) if a ≤ x ≤ b

g(x) if b ≤ x ≤ c

is continuous on [a, c].

H. Let f be a continuous real-valued function deﬁned on an open subset U of R

. Show

that {(x, y) : x ∈ U, y > f(x)} is an open subset of R

n+1

124 Functions

I. (a) Show that m(x, y) = max{x, y} is continuous on R

(b) Hence show that if f and g are continuous real-valued functions on a set S ⊂ R

then h(x) = max{f(x), g(x)} is continuous on S.

are continuous real-valued functions on S for

1 ≤ i ≤ k, then h(x) = max

1≤i≤k

(x) is continuous.

J. Show that a function f from R

into R

is continuous if and only if f

−1

for every closed set C ⊂ R

K. Suppose that A and B are subsets of R

. Find necessary and sufﬁcient conditions for

there to be a continuous function f on R

with f|

= 1 and f|

= 0.

HINT: Consider g(x) = dist(x, A) and h(x) = dist(x, B).

L. Give example of a continuous function f and an open set U such that f(U) is not open.

M. Suppose that f : R → R satisﬁes the functional equation

f(u + v) = f(u) + f (v) for all u, v ∈ R.

(a) Prove that f(mx) = mf(x) for all x ∈ R and m ∈ Z.

HINT: Use induction for m ≥ 1 and show that f(−x) = −f(x).

(b) Prove that f(x) = mx for all x ∈ Q, where m = f(1).

HINT: Use (a) to solve for f(p/q) when p, q ∈ Z.

5.4. Compactness and Extreme Values

In every calculus course, a lot of effort is spent ﬁnding the maximum or min-

imum of various functions. Sometimes there were physical reasons why such a

point should exist. However, generally it was taken on blind faith and the student

dutifully differentiates the function to ﬁnd critical points. Even when the function

is not differentiable, the function may attain its maximum value. On the other hand,

many very nice functions do not attain maxima. In this section, we will see how

our new topological tools can explain this phenomenon.

First consider a couple of easy examples in which there are no maxima.

5.4.1. EXAMPLE. Consider f(x) =

−1

1 + kxk

for x ∈ R

. This function is

bounded above, yet the supremum 0 = lim

kxk→∞

f(x) is never attained. The function

g(x) = kxk is unbounded and thus also does not attain its supremum. These

problems can occur whenever the domain of the function is unbounded.

5.4.2. EXAMPLE. Consider f(x) = −x for x ∈ (0, 1]. This function is

bounded above yet does not attain its supremum 0 = lim

x→0

f(x) because the limit

point 0 is missing from the domain. Similarly, the function f(x) =

for x ∈ (0, 1]

is unbounded and thus does not attain its supremum. A modiﬁcation of this exam-

ple would show that the same problem results whenever the domain is not closed.

5.4 Compactness and Extreme Values 125

Both of these difﬁculties may be avoided if the domain is compact. It turns out

that this is all that we need. As in most proofs using compactness, the aim is to ﬁnd

an appropriate sequence in the compact set C so that a convergent subsequence can

be obtained with good properties.

5.4.3. THEOREM. Let C be a compact subset of R

, and let f be a continuous

function from C into R

. Then the image set f (C) is compact.

PROOF. Let (y

)

∞

n=1

be a sequence in f (C). We must ﬁnd a subsequence con-

verging to a point in the image. First choose points x

in C such that y

= f (x

Now (x

)

∞

n=1

is a sequence in the compact set C. Therefore, there is a subsequence

) such that

lim

i→∞

= c ∈ C.

Therefore, by the continuity of f,

lim

i→∞

= lim

i→∞

f(x

) = f (c).

Thus the subsequence (y

) has the limit f(c) in f(C). Consequently, f(C) is

compact. ¥

This immediately yields a result often used (without proof) in calculus.

5.4.4. EXTREME VALUE THEOREM.

Let C be a compact subset of R

, and let f be a continuous function from C into

R. Then there are points a and b in C attaining the minimum and maximum values

of f on C. That is,

f(a) ≤ f(x) ≤ f(b) for all x ∈ C.

PROOF. Since C is compact, Theorem 5.4.3 shows that f(C) is compact. Hence it

is closed and bounded in R. Boundedness shows that

m = inf

x∈C

f(x) and M = sup

x∈C

f(x)

are both ﬁnite. From the deﬁnition of supremum, M is a limit of values in f(C).

Thus since f(C) is closed, M ∈ f(C). This means that there is a point b ∈ C

such that f(b) = M. Similarly, the inﬁmum is attained at some point a ∈ C. ¥

Exercises for Section 5.4

A. If A is a noncompact subset ofR

, show thatthere is a bounded continuous real-valued

function on A that does not attain its maximum.

B. Find a discontinuous function on [0, 1] that is bounded but does not achieve its supre-

mum.

C. Suppose that f is a continuous function on [a, b] with no local maximum or local

minimum. Prove that f is monotone.

126 Functions

D. Find a linear transformation T on R

and a closed subset C of R

such that T (C) is

not closed.

E. Show that a function f mapping a compact set S ⊂ R

into R

is continuous if and

only if its graph G(f) = {(x, f(x)) : x ∈ S} is compact.

HINT: For ⇒, use Theorem 5.4.3. For ⇐, use Theorem 5.3.1(2).

F. Give a function deﬁned on [0, 1] that has a closed graph but is not continuous.

G. Suppose that f is a positive continuous function on R

such that lim

kxk→∞

f(x) = 0

[i.e., for all ε > 0, there is an N so that |f(x)| < ε for all x with kxk > N]. Show

that f attains its maximum.

H. Let f be a periodic function on R, meaning that there is d > 0 with f(x + d) = f(x)

for all x ∈ R. (We call d the period of f if it is the least positive number with this

property and say that f is d-periodic.) Show that if f is continuous, then f attains its

maximum and minimum on R.

I. (a) Give an example of a continuous function on R

satisfying f (x + 1, y) = f(x, y)

for all x, y ∈ R that does not attain its maximum.

(b) Find and prove a variant of the previous exercise that is valid for functions on R

J. Let A be a compact subset of R

. Show that for any point x ∈ R

, there is a closest

point a in A to x. (This means that the point a ∈ A satisﬁes kx − ak ≤ kx − bk for

all b ∈ A. It does not imply that a is unique—it may not be.)

HINT: Fix x and deﬁne a useful continuous function on A.

K. For a function f on [0, ∞), we say that lim

x→∞

f(x) = L if for every ε > 0, there is

some N > 0 so that |f(x) − L| < ² for all x > N . Suppose that lim

x→∞

f(x) = f(0)

and that f is continuous. Prove that f attains its maximum and minimum values.

L. Suppose that C is a compact subset of R

and that f is a continuous, one-to-one

function of C onto D ⊂ R

. Prove that the inverse function f

−1

is continuous.

HINT: Fix d

∈ D, c

= f

−1

) and ε > 0. Show that there is a r > 0 so that B

)

is disjoint from f(C \ B

)).

M. A space-ﬁlling curve. Let T be a right triangle with side lengths 3, 4, and 5. Drop a

perpendicular line from the right angle to the opposite side, splitting the triangle into

two similar pieces. Label the smaller triangle T (0) and the larger one T (1). Then

divide each T (ε) into two pieces in the same way, labeling the smaller T (ε0) and the

larger T (ε1). Recursively divide each triangle T (ε

. . . ε

) into two smaller similar

triangles labeled T (ε

. . . ε

0) and T (ε

. . . ε

1). Now consider each point x ∈ [0, 1]

in its base 2 (binary) expansion x = 0.ε

. . . , where ε

is 0 or 1. Deﬁne a function

f : [0, 1] → T by deﬁning f(x) to be the point in

n≥1

T (ε

. . . ε

(a) Prove that T (ε

. . . ε

) has diameter at most 5(.8)

(b) If x = 0.ε

. . . ε

n−1

100000. . . has a ﬁnite binary expansion, then it has a second

binary representation x = 0.ε

. . . ε

n−1

011111. . . ending in ones. Prove that both

expansions yield the same value for f(x).

(d) Prove that f is continuous. HINT: If x and y agree to the nth decimal, what do

f(x) and f(y) have in common?

(e) Prove that f maps [0, 1] onto T .

5.5 Uniform Continuity 127

N. A space-ﬁlling curve II. Adapt the triangle ﬁlling function of the previous exercise to

construct a continuous function on R that maps onto the entire plane.

HINT: Consider covering the plane by triangles somehow.

5.5. Uniform Continuity

Mathematical terminology is not always consistent, but the adjective uniform is

(almost) always used the same way. A property is uniform on a set if that property

holds at every point in the set with common estimates. Uniform estimates often

lead to more powerful conclusions.

5.5.1. DEFINITION. A function f from S ⊂ R

into R

is uniformly contin-

uous if for every ε > 0, there is a positive real number r > 0 so that

kf(x) − f(a)k < ε whenever kx − ak < r, x, a ∈ S.

Read the deﬁnition carefully to note what makes it different from continuity at

each point a ∈ S. For f to be continuous, we ﬁx both ε > 0 and a ∈ S before

obtaining the value of r. So the choice of r might depend on a as well as on ε.

Uniform continuity means that for each ε > 0, the value r > 0 that we obtain can

be chosen independently of the point a. This is a subtle difference, so we look at

some examples.

5.5.2. EXAMPLE. Consider the function f(x) = x

deﬁned on the bounded

interval [c, d]. Let us try to obtain a common estimate for r for each ε > 0. Re-

member that we are trying to control the difference |f(x)−f(a)|only by controlling

|x −a|. Hence we always look for a method of getting a factor close to |x −a| into

our estimate while gaining some (perhaps crude) control over the rest. Compute

|f(x) − f(a)| = |x

− a

| = |x + a||x − a|.

In this case, the factor of |x − a| comes out naturally. A bound must be found for

|x + a|. Note that for any x ∈ [c, d], we have

|x| ≤ max{|c|, |d|} =: M.

Hence we can show that

|x + a| ≤ |x| + |a| ≤ 2M.

We are allowed to choose a positive number r and insist that |x −a| < r. With this

choice, the combined estimates yield

|f(x) − f(a)| = |x + a||x − a| < 2Mr.

To make this at most ε, it sufﬁces to choose r = ε/(2M ), whence

|f(x) − f(a)| < 2Mr = ε for all |x − a| < r, x, a ∈ [c, d].

Hence f is uniformly continuous.

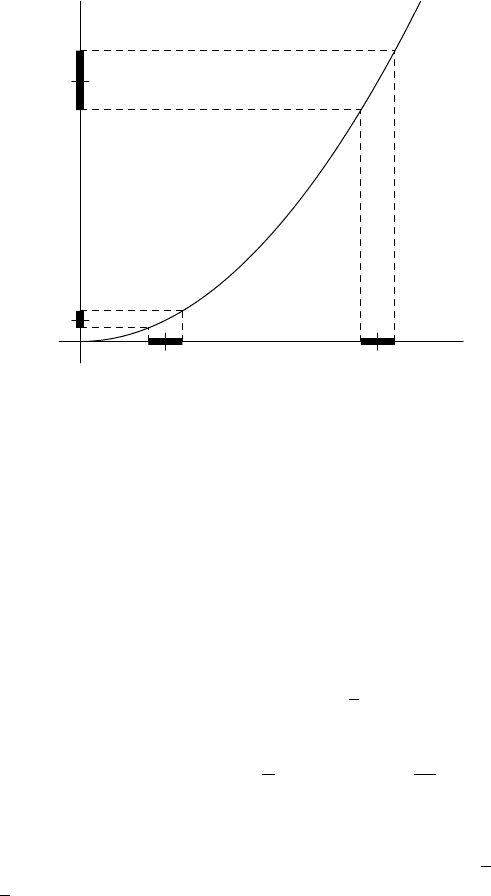
128 Functions

On the other hand, consider f (x) = x

deﬁned on the whole real line. The

preceding argument doesn’t work because M would be inﬁnite.

Intuitively, we can put it this way: Suppose, for a ﬁxed ε > 0, we had some

r > 0 that satisﬁes the deﬁnition of uniform continuity for f(x) = x

on R.

As Figure 5.6 suggests, as a goes to inﬁnity, the interval between f(a − r) and

f(a + r) will no longer be contained in the interval from f(a) − ε to f (a) + ε,

giving a contradiction. Since this happens for all r > 0, there is no choice of r that

“works.”

− r a

+ r

f(a

)

− r a

+ r

f(a

)

FIGURE 5.6. The function f(x) = x

on R.

In fact, the estimates used before show us how to make this precise. Suppose

that |x − a| = r. Then

|f(x) − f(a)| = |x

− a

| = |x + a||x − a| = |x + a| r.

When |x + a| is very large compared with 1/r, this difference will be large. It

suggests that for any choice of r, values of x and a can be found to violate our

hoped-for estimates. Search for a sequence that shows that r = 1/n won’t work

for each n ≥ 1. For example, let

= n and x

= n +

Then

|f(x

) − f (a

)| =

n +

− n

= 2 +

To violate the deﬁnition of uniform continuity, only one value of ε is needed

provided that it is shown that no value of r > 0 will work for that ε. In this case,

we may take ε = 1. For any r > 0, there is some n so large that

< r. Then

− a

| =

< r, yet |f(x

) − f(a

)| > 2 > ε. Therefore, f is not uniformly

continuous on R.

5.5 Uniform Continuity 129

5.5.3. EXAMPLE. Consider the function f(x) = 1/x on (0, 1]. Notice that the

graph blows up at the origin and becomes very steep. This is the same property that

we just exploited for x

as x goes off to inﬁnity. Very close values in the domain

are mapped to points which are far apart. Let x

. Then

|f(x

n+1

) − f(x

)| = (n + 1) − n = 1.

However, |x

n+1

− x

| =

n+n

tends to 0. So let ε = 1 and consider any r > 0.

For n large enough, |x

n+1

− x

| < r, but |f(x

n+1

) − f(x

)| = 1 = ε. So f is not

uniformly continuous.

A number of properties of functions imply uniform continuity.

5.5.4. PROPOSITION. Every Lipschitz function is uniformly continuous.

PROOF. Recall that f is Lipschitz on S means that there is a constant C such that

kf(x) − f(y)k ≤ Ckx − yk.

Given ε > 0, choose r = ε/C. Then if x, a ∈ S and kx − ak < r,

kf(x) − f(a)k ≤ Ckx − ak < C

= ε.

Thus uniform continuity is established (almost by deﬁnition). ¥

Corollary 5.1.7 shows that every linear transformation is a Lipschitz function

and Exercise 5.1.I shows that every function f : [a, b] → R with a bounded deriva-

tive is a Lipschitz function. Hence we obtain the following:

5.5.5. COROLLARY. Every linear transformation from R

to R

is uniformly

continuous.

5.5.6. COROLLARY. Let f be a differentiable real-valued function on [a, b]

with a bounded derivative; that is, there is M > 0 so that |f

(x)| ≤ M for all

a ≤ x ≤ b. Then f is uniformly continuous on [a, b].

Before getting to our main result, we look at two more examples. The ﬁrst is

to show that a function does not need to be unbounded in order to fail uniform con-

tinuity. However, the previous theorem shows us that the function should be very

steep (large derivative) frequently. This suggests returning to one of our favourite

functions.

5.5.7. EXAMPLE. Let f(x) = sin

on (0, 1]. A computation of the derivative

is not necessary since the qualitative features of this function have been considered

before. See Example 5.2.8. The function oscillates wildly between +1 and −1 as

130 Functions

x approaches 0. In particular,

lim

n→∞

(2n +

)π

= 1

and

lim

n→∞

(2n −

)π

= −1.

Let

(2n +

)π

and a

(2n −

)π

Then f(x

) − f (a

) = 2 for all n ≥ 1 while

lim

n→∞

− a

| = lim

n→∞

(4n

−

)π

= 0.

As before, this means that f is not uniformly continuous.

Finally, let us look at an example in which the derivative is unbounded yet the

function is still uniformly continuous.

5.5.8. EXAMPLE. Let f(x) = x sin

on (0, ∞), which we graph in Figure 5.7.

What makes this different from the previous examples is the behaviour at the end-

points. At 0, the Squeeze Theorem shows that

lim

x→0

x sin

= 0.

Thus we may deﬁne f(0) = 0 and obtain a continuous function on [0, ∞). At

inﬁnity, the substitution y =

yields

lim

x→∞

x sin

= lim

y→0

siny

= 1.

This latter limit is established in Example 2.3.7. In fact, we obtained the explicit

estimates

1 −

< x sin

< 1 for x ≥ 1.

We will show that f is uniformly continuous. The two limits will be used to

deal with points near 0 and near inﬁnity (sufﬁciently large). Let 0 < ε < 1 be

given. First consider values near the origin. If |x| < ε/2 and |y| < ε/2, then

|f(x) − f(y)| ≤ |x||sin

| + |y||sin

| ≤ |x| + |y| < ε.

Thus if x ∈ [0, ε/4] and |x − y| < ε/4, then this estimate holds.

Now do the same thing near inﬁnity. Pick an integer N > ε

−1/2

. If x and y are

greater than N, then

1 − ε < 1 −

< f(x) < 1.

The same is true for y, and thus if x ≥ N + 1 and |x − y| < 1, then

|f(y) − f(x)| < ε.

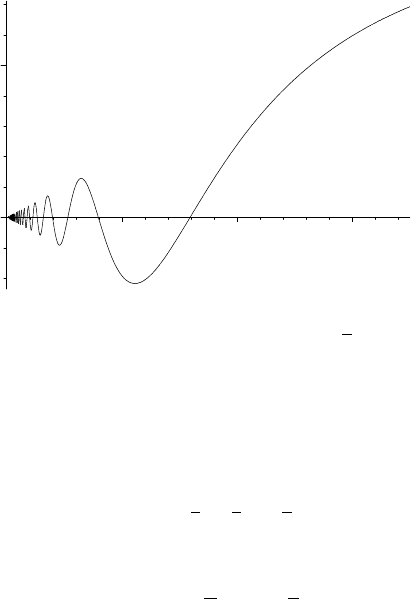
5.5 Uniform Continuity 131

0.5

0.2 0.4

0.6

FIGURE 5.7. Partial graph of x sin

These two estimates show that |f (y) − f(x)| < ε if |x − y| < ε/4 and either x or

y lies in either [0, ε/4] or [N + 1, ∞).

Now consider the case in which both x and y in the interval [ε/4, N + 1]. On

this interval, the function f has a continuous derivative

(x) = sin

−

cos

An easy estimate shows that

(x)| ≤ 1 +

≤ 1 +

Let M = 1 + 4/ε. Hence by Corollary 5.5.6, if we take |x − y| < ε/M and

ε/4 ≤ x, y ≤ N + 1, then |f (x) − f(y)| < ε. (We could also establish this case

using Theorem 5.5.9, but then we would not get an explicit estimate for r in terms

of ε.)

Finally, as ε/M = ε

/(4+ ε), we can choose r = min{ε/4, ε

/(4+ ε)}. Then

if |x−y| < r, one of the preceding estimates applies to showthat |f(y)−f (x)| < ε.

Therefore, f is uniformly continuous.

We conclude this section with an important result relating compactness to uni-

form continuity.

5.5.9. THEOREM. Suppose that C ⊂ R

is compact and f : C → R

continuous. Then f is uniformly continuous on C.

PROOF. Suppose that f were not uniformly continuous. Then there would be some

ε > 0 for which no r > 0 satisﬁes the deﬁnition. That is, for each r = 1/n, there

are points a

and x

in C such that kx

− a

k < 1/n but kf(x

) − f (a

)k ≥ ε.

Since C is compact and (a

)

∞

n=1

is a sequence in C, there is convergent subse-

quence (a

) with

lim

k→∞

= a ∈ C.

132 Functions

Thus we also have

lim

k→∞

= lim

k→∞

+ (x

− a

) = a + 0 = a.

By the continuity of f, we have

lim

k→∞

f(a

) = f (a) and lim

k→∞

f(x

) = f (a).

Consequently,

lim

k→∞

f(a

) − f (x

)

= 0.

This contradicts kf(a

) − f (x

)k ≥ ε > 0 for all n. Therefore, the function must

be uniformly continuous. ¥

Compare how the sequences (a

) and (x

) are used in this proof to how sim-

ilar sequences are used to show speciﬁc functions are not uniformly continuous in

Examples 5.5.3, 5.5.2, and 5.5.7.

Exercises for Section 5.5

A. Show that g(x) =

√

x is uniformly continuous on [0, +∞).

HINT: Show that

√

a − b ≥

√

a −

√

b and

√

a + b ≤

√

a +

√

B. Given a polynomial p(x, y) =

m,n=0

in variables x and y and an ε > 0, ﬁnd

an explicit δ > 0 establishing uniform continuity on the square [−R, R]

HINT: Try δ = ε/C, where C =

m,n=0

|(m + n)R

m+n−1

C. (a) Show that the function f(x) =

sinx for x 6= 0 can be extended to a continuous

function on all of R.

(b) Prove that it is uniformly continuous on R.

D. Show that f(x) = x

is not uniformly continuous on R if p > 1.

E. Show that if f is continuous on (0, 1) and lim

x→0

f(x) = +∞, then f is not uniformly

continuous.

F. Show that a periodic continuous function on R is bounded and uniformly continuous.

G. Suppose that f = (f

, . . . , f

) is a continuous function from an open subset S of R

into R

that has partial derivatives

∂f

∂x

(x)

≤ M < ∞ for all x ∈ S. Prove that f is

uniformly continuous.

H. Suppose that f is continuous on (a, c) and that a < b < c. Show that if f is uniformly

continuous on both (a, b] and [b, c), then f is uniformly continuous on (a, c).

HINT: Use ε/2 to get a δ for each interval separately.

I. Let f be a continuous function on (0, 1]. Show that f is uniformly continuous if and

only if lim

x→0

f(x) exists.

J. For which real values of α is the function g

(x) = x

log(x) uniformly continuous

on (0, ∞)? HINT: Use Exercises D, E, and H as a guide. For 0 < α < 1, consider

[0, 1] and [1, ∞) separately.