Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

4.4 Compact Sets and the Heine–Borel Theorem 103

Next consider the sequence y

= x

for j ≥ 1. This sequence is contained

in the closed interval [a, b]. Thus a second application of the Bolzano–Weierstrass

Theorem yields a subsequence (y

) = (x

) such that lim

l→∞

= z

. We still

have lim

l→∞

= z

since every subsequence of a convergent sequence has the

same limit.

Proceeding in this way, ﬁnding n consecutive sub-subsequences, we obtain a

subsequence p

< p

< . . . and z

in [a, b] such that

lim

j→∞

= z

for 1 ≤ i ≤ n.

Thus lim

j→∞

= z := (z

, . . . , z

) by Lemma 4.2.3. ¥

4.4.6. THE HEINE–BOREL THEOREM.

A subset of R

is compact if and only if it is closed and bounded.

PROOF. The easy direction is given by Lemma 4.4.3.

For the other direction, suppose that C is a closed and bounded subset of R

Since it is bounded, there is some M > 0 so that kxk ≤ M for all x ∈ C. In

particular, C is contained in the cube [−M, M]

. Now [−M, M ]

is compact by

Lemma 4.4.5. So C is a closed subset of a compact set and therefore is compact by

Lemma 4.4.4. ¥

This leads to an important generalization of the Nested Interval Theorem.

4.4.7. CANTOR’S INTERSECTION THEOREM.

If A

⊃ A

··· is a decreasing sequence of nonempty compact subsets of

, then

k≥1

is not empty.

PROOF. Since A

is not empty, we may choose a point a

in A

for each n ≥ 1.

Then the sequence (a

)

∞

n=1

belongs to the compact set A

. By compactness, there

is a subsequence (a

)

∞

k=1

that converges to a limit point x. For each i, the terms

belong to A

for all k ≥ i. Thus x is the limit of points in A

, whence x belongs

to A

for all i ≥ 1. Therefore, x belongs to their intersection. ¥

4.4.8. EXAMPLE: THE CANTOR SET. We now give a more subtle example

of a compact set in R. The Cantor set is a fractal subset of the real line. Let

= [0, 1], and construct S

i+1

from S

recursively by removing the middle third

from each interval in S

. For example, the ﬁrst three terms are

= [0, 1/3] ∪ [2/3, 1]

= [0, 1/9] ∪ [2/9, 1/3] ∪ [2/3, 7/9] ∪ [8/9, 1]

= [0, 1/27] ∪ [2/27, 1/9] ∪ [2/9, 7/27] ∪ [8/27, 1/3]

∪ [2/3, 19/27] ∪ [20/27, 7/9] ∪ [8/9, 25/27] ∪ [26/27, 1]

104 Topology of R

By Proposition 4.3.3, the intersection C = ∩

i≥1

is a closed set. It is bounded and

hence compact. By Cantor’s Intersection Theorem, this intersection is not empty.

Figure 4.3 shows an approximation to the Cantor set, namely S

0 1

FIGURE 4.3. The Cantor set (actually S

Every endpoint of an interval in one of the sets S

belongs to C. But in fact,

C contains many other points. Each point in C is determined by a binary decision

tree. At the ﬁrst stage, pick one of the two intervals of S

of length 1/3, which we

label 0 and 2. This interval is split into two in S

by removing the middle third.

Choose either the left (label 0) or right (label 2) to obtain an interval labeled 00,

02, 20, or 22. Continuing in this way, we choose a decreasing sequence of intervals

determined by an inﬁnite sequence of 0s and 2s. By Cantor’s Intersection Theorem

(Theorem 4.4.7), every choice determines a point of intersection. There is only one

point in each of these intersections because the length of the intervals tends to 0.

We leave it to you to describe the (proper) set of decision trees that correspond to

left or right endpoints.

The Cantor set has empty interior. For if C contained an open interval (a, b)

with a < b, it would also be contained in each S

. This forces b − a ≤ 3

−n

for

every n, whence a = b. So the interior of C is empty. A set whose closure has no

interior is nowhere dense.

Yet C has no isolated points. A point x of a set A is isolated if there is an

ε > 0 such that the ball B

(x) intersects A only in the singleton {x}. In fact, C

is a perfect set, meaning that every point of C is the limit of a sequence of other

points in C. In other words, every point is a cluster point. To see this, suppose

ﬁrst that x is not the right endpoint of one of the intervals of some S

. For each

n, let x

be the right endpoint of the interval of S

containing x. Then x

6= x

and |x

− x| ≤ 3

−n

. So x = lim

n→∞

. If x is the right endpoint of one of these

intervals, use the left endpoints instead to deﬁne the sequence x

The set C is very large, the same size as [0, 1], in the sense of cardinality from

Appendix 2.8. Consider the numbers in [0, 1] expanded as inﬁnite “decimals” in

base 3 (the ternary expansion). That is, each number may be expressed as

x = (x

. . . )

base 3

k≥0

−k

where x

belong to {0, 1, 2} for i ≥ 1. Note that S

consists of all numbers in [0, 1]

that have an expansion with the ﬁrst digit equal to 0 or 2. In particular,

= (.1)

base 3

= (.02222222 . . . )

base 3

and 1 = (.22222222 . . . )

base 3

Likewise, S

consists of all numbers in [0, 1] such that the ﬁrst i terms of some

ternary expansion are all 0s and 2s. Since C is the intersection of all the S

, it

consists of precisely all the numbers in [0, 1] that have a ternary expansion using

only 0s and 2s.

4.4 Compact Sets and the Heine–Borel Theorem 105

As C is a subset of [0, 1], it is clear that C can have no more points than [0, 1].

To see that [0, 1] can have no more points than C, we construct a one-to-one map

from [0, 1] into C. Think of the points in [0, 1] in terms of their binary expansion

(base 2). These are all the “decimal” expansions

y = (y

. . . )

base 2

k≥0

−k

where y

∈ {0, 1}. For each point, pick one binary expansion. (Some numbers

have two possible expansions, one ending in an inﬁnite string of 0s and the

other ending in an inﬁnite string of 1s. In this case, pick the expansion ending in

0s.) Send it to the corresponding point in base 3 using 0s and 2s by changing each

1 to 2. Since this corresponding point is in C, we have a map of [0, 1] into C. This

map is one-to-one because the only duplication of ternary expansions comes from

a sequence ending in all 0s corresponding to another ending with all 2s. But we do

not send any number to a ternary expansion ending in all 2s.

Warning: This map is not onto because of numbers with two expansions in

base 2 such as

, which in base two equals both (.1)

base 2

and (.01111. . . )

base 2

We only used the ﬁrst one, which we send to (.2)

base 3

, namely

. But the other

expansion would go to (.02222 . . . )

base 3

, which equals (.1)

base 3

At this point, it seems obvious that there are as many points in C as in [0, 1]—it

can’t have any more, and it can’t have any less. However, with inﬁnite sets, proving

this is a subtle business. The Schroeder–Bernstein Theorem (Theorem 2.8.8) could

be invoked to obtain a bijection between C and [0, 1]. However, the special nature

of our setup allows a bijection between C and [0, 1] to be constructed fairly easily;

see Exercise 4.4.K. Therefore, C and [0, 1] have the same cardinality, which is

uncountable by Theorem 2.8.7.

On the other hand, using a different notion of “size,” the Cantor set is very

small. We can measure how much of the interval has been removed at each step.

The set S

contains 2

intervals of length 3

−n

. The middle third of length 3

−n−1

is removed from each of these 2

intervals to obtain S

n+1

. The total length of the

pieces removed is computed by adding an inﬁnite geometric series

∞

n=0

n+1

1/3

1 − (2/3)

= 1.

Thus the Cantor set has measure zero, a notion that is discussed in Section 6.6. In

some sense, C squeezes its very large number of points into a very small space.

Exercises for Section 4.4

A. Which of the following sets are compact?

(a) {(x, y) ∈ R

: 2x

− y

≤ 1}

(b) {x ∈ R

: 2 ≤ kxk ≤ 4}

−x

cosx, e

−x

sinx) : x ≥ 0} ∪ {(x, 0) : 0 ≤ x ≤ 1}

(d) {(e

−x

cosθ, e

−x

sinθ) : x ≥ 0, 0 ≤ θ ≤ 2π}

106 Topology of R

B. Give an example to show that Cantor’s Intersection Theorem would not be true if

compact sets were replaced by closed sets.

C. Show that the union of ﬁnitely many compact sets is compact.

D. Show that the intersection of any family of compact sets is compact.

E. (a) Show that the sum of a closed subset and a compact subset of R

is closed. Recall

that A + B = {a + b : a ∈ A and b ∈ B}.

(b) Is this true for the sum of two compact sets and a closed set?

F. Let (x

)

∞

n=1

be a sequence in a compact set K that is not convergent. Show that there

are two subsequences of this sequence that are convergent to different limit points.

G. Prove that a set S ⊂ R has no cluster points if and only if S ∩[−n, n] is a ﬁnite set for

each n ≥ 1.

H. Describe all subsets of R

that have no cluster points at all.

I. Let A and B be disjoint closed subsets of R

. Deﬁne

d(A, B) = inf{ka − bk : a ∈ A, b ∈ B}.

(a) If A = {a} is a singleton, show that d(A, B) > 0.

(b) If A is compact, show that d(A, B) > 0.

with d(A, B) = 0.

J. The Sierpinski snowﬂake is constructed in the plane as follows. Start with a solid

equilateral triangle. Remove the open middle triangle with vertices at the midpoint of

each side of the larger triangle, leaving three solid triangles with half the side length

of the original. From each of these three, remove the open middle triangle, leaving 9

triangles of one fourth the original side lengths. Proceed in this process ad inﬁnitum.

Let S denote the intersection of all the ﬁnite stages.

FIGURE 4.4. The third stage in constructing the Sierpinski snowﬂake.

(a) Show that S is a nonempty compact set.

(b) Show that S has no interior.

that there is a path in S from the top vertex of the original triangle that gets as close

as desired (within ε) to any point in S.

(d) Compute the area of the material removed from the triangle to leave S behind.

(e) Construct a decision tree for S. Does each decision tree correspond to exactly one

point in the set? Show that S is uncountable.

4.4 Compact Sets and the Heine–Borel Theorem 107

K. Show that there is a bijection from [0, 1] onto the Cantor set.

HINT: Adjust the map constructed in the text by redeﬁning it on a countable sequence

to include the missing points in the range.

L. Prove that a countable compact set X = {x

: n ≥ 1} cannot be perfect.

HINT: Use a decreasing family X

of closed nonempty subsets of X with x

6∈ X

CHAPTER 5

Functions

The main purpose of this chapter is to introduce the notion of a continuous function.

Continuity is a basic notion of analysis. It is only with continuous functions that

there can be any reasonable approximation or estimation of valuesat speciﬁc points.

Most physical phenomena are continuous over most of their domain. The ideas we

study in this chapter are sufﬁciently powerful that even discrete phenomena are

sometimes best understood by using continuous approximations, where these ideas

can be used.

5.1. Limits and Continuity

General functions, between any two sets, were deﬁned in Section 1.2. In this

chapter, and indeed in most of this book, functions will be deﬁned on some subset

S of R

with range contained in R

. Everything is based on the notion of limit,

which is a natural variant of the deﬁnition for limit of a sequence.

5.1.1. DEFINITION OF LIMIT. Let S ⊂ R

and let f be a function from S

into R

. If a is a limit point of S \ {a}, then a point v ∈ R

is the limit of f at a

if for every ε > 0, there is an r > 0 so that

kf(x) − vk < ε whenever 0 < kx − ak < r and x ∈ S.

We write lim

x→a

f(x) = v.

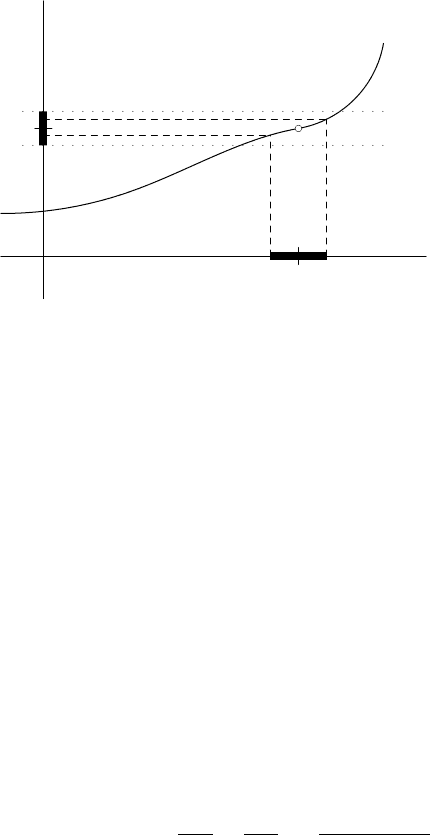
Geometrically, we have a picture such as Figure 5.1. Notice that f(a) itself

need not be deﬁned. Certainly, saying that lim

x→a

f(x) = v does not tell us anything

about f(a).

Let us specialize to the case of a real-valued function f deﬁned on an interval

(a, b) and let c be a point in this interval. Then lim

x→c

f(x) = L means that for every

ε > 0, there is an r > 0 so that

|f(x) − L| < ε for all 0 < |x − c| < r.

108

5.1 Limits and Continuity 109

y = f(x)

a − r a + r

v − 

v + 

FIGURE 5.1. Limit for a function f : R → R.

5.1.2. DEFINITION. Let S ⊂ R

and let f be a function from S into R

. We

say that f is continuous at a ∈ S if for every ε > 0, there is an r > 0 such that,

for all x ∈ S with kx − ak < r, we have kf(x) − f (a)k < ε. Moreover, f is

continuous on S if it is continuous at each point a ∈ S.

If f is not continuous at a, we say that f is discontinuous at a.

Continuity can sometimes be described using a limit. If a is an isolated point

of S, then f is always continuous at a. If a is not an isolated point, i.e., a is a limit

point of S \{a}, then lim

x→a

f(x) makes sense and f is continuous at a if and only if

lim

x→a

f(x) = f(a).

5.1.3. EXAMPLE. Consider the function f : R

\ {0} → R given by

f(x) = 1/kxk.

Let us show that this is continuous on its domain. Fix a point a ∈ R

\ {0}. Then

|f(x) − f(a)| =

kxk

−

kak

kak − kxk

kxkkak

Our goal is to make this difference small only by controlling the distance from x to

a, namely kx − ak.

The ﬁrst step is to show that the numerator is controllable. Indeed, what we

need follows from the triangle inequality.

kxk ≤ kak + kx − ak and kak ≤ kxk + kx − ak.

Manipulating these inequalities yields

−kx − ak ≤ kxk − kak ≤ kx − ak.

Hence

kxk − kak

≤ kx − ak. This takes care of the numerator.

Now let’s worry about the denominator kxkkak. Since kak is a positive con-

stant, it creates no problems. However, kxk must be kept away from 0 to keep the

110 Functions

quotient in control. This is accomplished by making x sufﬁciently close to a. The

previous paragraph shows that

kxk ≥ kak − ka − xk,

so provided that ka − xk < kak/2, we obtain kxk > kak/2.

Putting all of this together, choose r ≤ kak/2 and consider all x so that

kx − ak < r. Then, remembering that making the denominator smaller makes

the quotient larger, we have

|f(x) − f(a)| =

kak − kxk

kxkkak

≤

kx − ak

kak

To make this less than ε, choose r ≤ εkak

/2. Combining this with our other

condition on r, it follows that

r = min

kak

εkak

is sufﬁcient to ensure that kf (x) − f(a)k < ε.

This shows that f is a continuous function. Notice that the function goes to

inﬁnity at 0. So the limit at 0 does not exist.

5.1.4. EXAMPLE. A function does not need to have a simple analytic expression

to be continuous. However, extra care needs to be taken at the interface. Consider

the function graphed in Figure 5.2, given by

f(x) =

(

0 if x ≤ 0

−1/x

if x > 0.

0.5

FIGURE 5.2. Graph of e

−1/x

for x > 0.

When a < 0 and ε > 0 is any positive number, we may take r = |a|. For if

|x − a| < |a|, then x < 0 and thus

|f(x) − f(a)| = |0 −0| = 0 < ε.

Therefore, f is continuous at a.

5.1 Limits and Continuity 111

Now if a > 0, ﬁnding an appropriate r for each ε is similar to the previous

example. This is an example of a function that is the composition of the more

elementary functions g(x) = e

and h(x) = −1/x, so that f(x) = g(h(x)). We

shall see shortly that the composition of continuous functions is continuous. This

simpliﬁes the exercise to showing that both g and h are continuous. We leave these

details to the reader.

Finally, we must consider a = 0 separately because the function f has different

deﬁnitions on each side of 0. Fix ε > 0. We use the fact that e

is an increasing

function such that lim

x→−∞

= 0, which follows from the basic properties of the

exponential function established in calculus. It follows that there is a large negative

number −N such that e

−N

< ε. Therefore, if 0 < x < 1/N, it follows that

−1/x < −N and thus

0 < f (x) = e

−1/x

< e

−N

< ε.

So take r = 1/N. We obtain

|f(x) − f(0)| =

(

0 < ε if − r < x ≤ 0

−1/x

< ε if 0 < x < r.

Hence f is continuous at a = 0.

As a further example, we treat a general class of useful functions that are auto-

matically continuous.

5.1.5. DEFINITION. A function f from S ⊂ R

into R

is called a Lipschitz

function if there is a constant C such that

kf(x) − f(y)k ≤ Ckx − yk for all x, y ∈ S.

The Lipschitz constant of f is the smallest choice of C for which the previous

condition holds.

As a matter of course, you should check that the Lipschitz constant is well

deﬁned. The following easy result will have several important consequences.

5.1.6. PROPOSITION. Every Lipschitz function is continuous.

PROOF. Let f be a Lipschitz function with constant C. Given ε > 0, let r = ε/C.

Then if kx − yk < r,

kf(x) − f(y)k ≤ Ckx − yk < Cr = ε.

Therefore, f is continuous. ¥

5.1.7. COROLLARY. Every linear transformation A from R

to R

is Lips-

chitz, and therefore is continuous.

112 Functions

PROOF. Recall that every linear transformation is given by an m ×n matrix, which

we also call A =

. The function is then given by the matrix multiplication

formula

A(x

, x

, . . . , x

) =

j=1

, . . . ,

j=1

Let x = (x

, x

, . . . , x

) and y = (y

, y

, . . . , y

). Compute

kAx − Ayk = kA(x − y)k

= kA(x

− y

, x

− y

, . . . , x

− y

i=1

j=1

− y

)

1/2

Apply the Schwarz inequality to obtain that

j=1

− y

)

≤

j=1

− y

j=1

kx − yk

Putting this into our computation, we get

kAx − Ayk ≤

i=1

j=1

1/2

kx − yk = Ckx − yk,

where

C =

i=1

j=1

1/2

Therefore, linear maps are Lipschitz, and hence are continuous. ¥

There are two basic linear functions, called coordinate functions, which we

will use regularly. There is the map π

, . . . , x

) = x

, which maps R

into R

by reading off the jth coordinate. And there is the map ²

(t) = te

, which maps

R into R

by sending R onto the ith coordinate axis. In Exercise 5.1.K, you are

asked to show that every linear map can be built up as linear combinations of ²

Exercises for Section 5.1

A. Use the ²–r deﬁnition of the limit of a function to show lim

x→2

= 4.

B. Show that the function

f(x) =

(

sinx

if 0 < |x| < π/2

1 if x = 0

is continuous at 0. Find an r > 0 such that |f(x) − 1| < 10

−6

for all |x| < r.

HINT: Use inequalities from Example 2.3.7.