Дамаскин Б.Б., Петрий О.А., Подловченко Б.И. и др. Практикум по электрохимии

Подождите немного. Документ загружается.

При обработке экспериментальных данных необходмо принимать

во внимание систематические ошибки Э

возникающие, например, из-

за использования приборов определенного класса точности (весы,

термометры, вольтметры и т.д.). Обычно такого рода погрешности рас-

считывают по формуле

е (

)

где

е _ суммарная неисключенная (систематическая) погрешность.

При Ро = 0,95 принимают к

= 1,1.

Знание систематической

погрешности позволяет решить практи-

ческую задачу определения числа повторных измерений, которые надо

провести для того, чтобы погрешность была наименьшей. Увеличение

числа измерений снижает случайную ошибку. При этом систематиче-

ская погрешность' от п не зависит. Если эта погрешность равна 6, то

число измерений следует выбрать таким, чтобы ширина доверитель-

ного интервала [(Д =-• I (р

, п— 1) У п] составляла - 50—100%

неисключенной систематической погрешности. Дальнейшее увели-

чение п будет приводить к уменьшению случайной погрешности, одна-

ко суммарная погрешность все равно будет,больше А. Соответствую-

щее неравенство для выбора оптимального п выглядит так:

п —1) Г~<

уп

Например, из табл. 1.4 видно, что при р

= 0,95 коэффициент Стью-

дента после п = 4 уменьшается слабо, следовательно, доверительный

интервал сужается медленно (примерно пропорционально 1 /}Гп).

В связи с этим не имеет смысла, особенно если эксперимент трудоем-

кий, проводить более 4—5 измерений.

Очевидно, что если в результате расчета случайной и систематиче-

ской погрешностей окажется, что одна из них существенно превышает

Другую, то малой можно пренебречь. Принято такое правило: при

В/з

< 0,8 пренебрегают систематической погрешностью, при 0/$р>8—

случайной. Если же 0,8< 6/$

< 8, то суммарная погрешность рас*

считывается по формуле

А ' •

2 3 /•"^ГеГ

- • V 2 г

Окончательный результат представляется в виде

(1.72)

(1-73)

(1.74)

122

где А в зависимости от соотношения систематической и случайной по-

грешностей рассчитываются по формулам: *

& =

}(Ро>

Л—1) в

При (0/$

<0,8), (1.75)

при (0,8<0/5

<8), (1.76)

при '(в/з

>8). (1.77)

Оценка результатов косвенных измерений. Часто возникает необ-

ходимость получить интересующую нас величину на основании извест-

ной ее связи с непосредственно измеряемой. Такие измерения называ-

ют косвенными. Пусть

.... х

), (1.78)

где у — функция измеряемых величин х

п1

. Обычно использу-

ют два приема для определения среднеарифметического величины у

и расчета погрешностей А у. В первом способе по каждому новому зна-

чению х

рассчитывают у

(

и затем выборку у( обрабатывают (см. с.

58). Во втором способе по результатам измерений находят х

и со-

ответствующие погрешности А^. Затем \ подставляют в формулу

<1.78) и рассчитывают у. Погрешность определяют по формуле

В большинстве практических случаев оба метода дают не сильно

различающиеся результаты. Чаще используют второй путь, посколь-

ку в нем объем вычислений меньше. Однако с теоретической точки зре-

ния правильным является только первый способ. Этот вывод следует

из того, что в общем случае М[ (I) ф / Щ1).

В заключение отметим, что хотя процедура первичной обработки

экспериментальных данных представляется весьма громоздкой, даже

на простых вычислительных машинах имеются или легко составляют-

ся соответствующие программы расчетов. С их помощью описанная

обработка данных практически не отнимает времени.

Определение параметров функциональной зависимости. На прак»

тике перед исследователем постоянно возникает задача построения по

опытным данным аналитических моделей. Если аналитический вид за-

висимости одной измеряемой величины у от другой л; известен, то дан-

ная задача сводится к отысканию по экспериментальным данным, по-

лучаемым с определенной погрешностью, наиболее подходящих пара-

метров этой зависимости. Примером такого рода задач в электрохимии

является анализ кривых ток — потенциал, емкость двойного электри-

ческого слоя — потенциал, составляющие импеданса — частота пере-

менного тока, поверхностное натяжение — концентрация органиче-

ского вещества и т. д.

Наиболее простым решением является поиск параметров линейной

зависимости, и мы остановимся на нем наиболее подробно.

61$

Метод наименьших квадратов. Пусть имеется набор значений Хг

и соответствующих им значений у

и связь между ними задана линей-

ным уравнением

= ах +

Ь.

(1.80)

Так как измерения у

и х

проводятся с погрешностями, то очевидно,

что

— 0-81)

где г

зависят от случайных погрешностей эксперимента и выбора пара-

метров а и Ь. Составим сумму

2 =

•

2 (У1-™1-

1 =

1=1

(1.82)

и будем искать такие а и Ь, при которых выражение (1.82) примет ми-

нимальное значение. Очевидно, что при рассчитанных таким образом

а и

прямая, представленная уравнением (1.80), наилучшим образом

[в смысле, заложенном в условии (1.82)] опишет нам эксперименталь-

ные данные. Параметры а и

в соответствии с необходимым условием

для минимума функции определяются из равенства нулю производ-

ных по а и Ь выражения (1.82):

да

дЬ

СУ*—«хг*

—Ь>»|—Д С1Г*———0.

| 2. СвП—ТО—2 2 «I—=0.

(1.83)

Отсюда следует

1а21 + п6 = 2

где 2*1 = 2!, 2*? =

«' = =

/ =

1 1'= I

-1=1

1=-.

Решая систему (1.84), имеем

а-

п2

—

(1.85)

2, 2,-2^

(1 86)

я2

-(2

)

Случайные погрешности параметров а и Ъ находят по формулам:

Да«*(р

. О

а, (1.87)

О-

)

где I (ро, /) —коэффициент Стьюдента при заданной доверительной

вероятности р

и степенях свободы* / = и ~ 2, а $

и 5

— средне-

квадратичные отклонения а и &, вычисляемые по формулам:

)

/ 2 (л-м)*

' ' п—2 •

(19,

Здесь у и необходимые для расчета $

, представляют собой значения у

вычисленные с использованием полученных а и

по соотношению (1.80)

при соответствующих хг. Величина 5

характеризует рассеяние экспе-

риментальных точек относительно теоретически полученной прямой.

Важным моментом является оценка значимости параметров а я Ь,

Для этого вычисляют

а| |6|

«а

которые сопоставляют с коэффициентом распределения Стьюдента

при данной доверительной вероятности р

и п — 2 степенях свободы.

Если (

а<

(р

, п — 2), 1

> I (р

> п — 2), то коэффициенты а и 6

значимы. В противном случае один из них исключается из соотноше-

ния (1.80). На практике это получается, если, например, рассчитан-

ный параметр а мал по абсолютной величине, а границы доверительного

интервала [см. уравнение (1,87)1 велики. В таком случае учитывать его

не имеет смысла и уравнение у ~ Ь хорошо описывает эксперименталь-

ные данные. Если незначим параметр Ь, то у ~ ах

Наряду с указанными характеристиками иногда рассчитывают ко-

эффициент корреляции. Теоретическое выражение для коэффициента

корреляции двух случайных величин I яц имеет вид

~ ущщ •

9Э)

* Число степеней свободы / представляет собой разность п ~~ р

где п —

число измерений; р — число параметров. Так как для прямой р = 2, то / ~

= л — 2. При вычислениях среднеарифметического р = I и, следователь-

но, [ — п —

32 12$

В нашем варианте коэффициент корреляции приближенно может быть

рассчитан по уравнению

/^ЕИг. (1,94)

у п2

—

)

где 2

2 УЬ

Близость |р| к единице указывает на линейную зависимость экспе-

риментальных значений у

от**.

Отметим, что соответствующим выбором координат зачастую мож-

но весьма сложные зависимости свести к линейным и рассчитать пара-

метры этой зависимости (например, так поступают при анализе зависи-

мостей тока от потенциала в тафелевских координатах Е = I и т. д.).

Аппроксимация полиномами.. Когда не удается опйсать экспери-

ментальные данные с помощью линейной зависимости (на это, напри-

мер, указывает рассчитанное по (1.94) |р|, которое оказывается зна-

чительно меньше 1), используют другие виды аппроксимирующих

функций. Наиболее часто применяют полиномы

к—О

Принципиально путь расчета параметров а

в этом случае не отлича-

ется от изложенного для аппроксимации данных линейной функцией.

Рассмотрйм вопрос об оптимальной степени полинома. Очевидно,

что при числе экспериментальных точек п на единицу большем, чем сте-

пень к, можно подобрать единственный полином, точно проходящий

через все точки. Другими словами, через две точки можно провести

прямую, через три точки — параболу второго порядка, через четыре

хочки

_кубическую параболу и т. д. При этом, конечно, 2

Вычисление параметров таких полиномов используют для интерполя-

ции, т. е. для нахождения значений в промежуточных точках функции*

заданной, например* в виде таблицы. Однако для наших целей такое

решение не имеет большого смысла, поскольку реальные измерения

проводятся с определенными погрешностями. С другой стороны, если

степень полинома слишком мала, то для аппроксимации эксперимен-

тальной зависимости ее может не хватить. Например, не имеет смысла,

учитывая близкую к параболической зависимость поверхностного на-

тяжения от потенциала на Н§-электроде, использовать для ее описания

линейную функцию. Таким образом, следует предположить, что для

описания экспериментальных зависимостей существует некоторая оп-

тимальная степень полинома.

€4

Практически такая задача обычно решается следующим образом.

Определяются коэффициенты а

полинома степени т, при которых ре-

ализуется минимум среднеквадратичного отклонения

п / га \ 2

2 - (1-96)

1—1 \ к —О ]

путем решения соответствующей системы линейных уравнений и со-

поставляют б

с погрешностями эксперимента е.-Если б

> е, то

это означает, что полученный полином плохо описывает эксперимен-

тальные данные и надо увеличить степень т. Если 6

<С е, то стар-

шие члены полинома (высокие степени) не достоверны и степень по-

линома надо уменьшить, т. е. необходимо добиться, чтобы 6

^ е.

При этом т должно быть много меньше числа точек п. Статистический

подход к задаче оптимальной степени полинома или другой аппрокси-

мирующей функции основан на сопоставлении выборочных дисперсий.

Такое сопоставление проводится с использованием критерия Фишера.

Поясним это сначала на более простом примере. Пусть одна и та же

величина измеряется двумя методами. С помощью первого из них прове-

дено к измерений и вычислена

1 ^

• " 1=

а с помощью второго — / измерений и вычислена

2 И^Т- -О'

)

Можно ли отдать предпочтение второму методу, если > ф? Ответ

на этот вопрос можно получить, сопоставив 8Уз1> с критерием Фише-

Р (/1, /

ро),

где = к — 1, /

= / — 1, /7

— доверительная веро-

ятность. Критерий Фишера Р (/

, р

) теоретически рассчитывают на

основании функции распределения Фишера, которой характеризуется

случайная величина и представляют в специальных таблицах.

Отметим, что в отношении в числителе должна стоять большая

из величин 8%>. Это связано с асимметричностью функции рас-

пределения Фишера и, следовательно, критерия Фишера (так как

> 0, то 81/81- не может быть отрицательной), т. е. Р (/

, /

,/?

) Ф

Ф Р (/

, Ро). Если

—Г->Р</1," 1%, РоЬ (1.99)

х'

то с вероятностью р

можно утверждать, что первая дисперсия боль-

ше второй и, таким образом, действительно, второй метод предпочти-

телен. В противном случае дисперсии считаются однородными и отдать

предпочтения ни одному из методов нельзя, т. е. полученные различия

могли иметь случайный характер.

3 Зак. 434

В задаче об оптимальной степени полинома сопоставляются по

критерию Фишера выборочная дисперсия 8%

= Ц вы-

борочная дисперсия единичных измерений Смысл величины 5?

очевиден — она отражает точность измерений у

при соответствую-

щих х

. Так, если при х

проведено п

измерений и получено п

значе-

ний у

(/= 1, ...,%), то

Если

2 "

— >?(/!> /А, РО> (1.100)

.....

для всех I (или тех, при которых проводились специальные измерения

для определения 51), то погрешности самой аппроксимации превышают

экспериментальные и степень полинома следует увеличить. Заметим,

что в качестве числа степеней свободы используется .= п — т—1.

Очевидно, что с ростом т уменьшается $%г и при некотором т

пере-

станет быть значимым по критерию Фишера, хотя бы для одного г. Ес-

ли такое т

найдено и /л

< я, то полученный полином хорошо аппрок-

симирует экспериментальные данные. Если т

близко к я, то в этом

случае следует сделать вывод, что экспериментальные данные не могут

быть описаны полиномом и необходимо искать другой вид аппроксими-

рующей функции.

Применение численных методов для решения ряда практических

задач. На практике при обработке экспериментальных данных иссле-

дователи зачастую сталкиваются с необходимостью проведения таких

операций, как дифференцирование, интегрирование, сглаживание по-

лученных на опыте зависимостей. Применение численных математиче-

ских методов в сочетании с использованием возможностей современной

вычислительной техники позволяет существенно ускорить и повысить

точность этих операций.

Численное

дифференцирование. Решение задачи численного диффе-

ренцирования экспериментальных зависимостей основывается на ме-

тодах аппроксимации (см. с. 64). Другими словами, поскольку аналити-

ческий вид экспериментальной зависимости у (х^ (где I име-

ет значения от 0 до л, а п+ 1—число точек), которую предстоит диф-

ференцировать, чаще всего неизвестен, то подбирают аппроксимирую-

щую у (х) функцию ф (х, а), где а — некоторые подгоночные парамет-

ры. Полагают, что у (х) = ср (х, а) и далее рассчитывают в нужных

точках производную ср' (.х, а), которую приравнивают к у' (х).

Не будем здесь останавливаться на строгом рассмотрении математи-

ческих проблем, связанных с проведением численного дифференциро-

вания. Заметим лишь, что эта операция требует определенной аккурат-

ности, так как производная представляет собой предел отношения при-

324

ращения функции к приращению аргумента, в связи с чем приращения

функций надо вычислять на возможно более узком интервале прира-

щения аргументаПри этом большое влияние могут оказывать экспе-

риментальные погрешности. Действительно, при малом изменении ар-

гумента приращение функции есть не что иное, как разность двух боль-

ших величин. Это обстоятельство может исказить точность получае-

мых результатов. Именно поэтому, например, на практике не исполь-

зуют аппроксимацию экспериментальных точек интерполяционными

многочленами, проходящими через все точки. Обычно дифференциро-

ванию предшествует сглаживание исходных данных. Цель сглажива-

ния — учесть возможные погрешности эксперимента и тем самым сни-

зить их влияние на расчет производных. Сглаживание обычно прово-

дят методом наименьших квадратов.

Практически поступают так. Рассчитывают параметры полинома,

степень которого меньше числа точек (об оптимальной степени полино-

ма см. с. 64) и который хорошо аппроксимирует исходные данные, а

затем в выбранных точках аналитически находят производную. Если

такой полином подобрать не удается, то сглаживание ведут «по кусоч-

кам». Пусть, например, точки х

распределены равномерно, т. е. мож-

но положить, что — = к (в принципе равномерное распреде-

ление не обязательно). Через первые три последовательные точки ме-

тодом наименьших квадратов проводят прямую и значение у

в средней

точке заменяют соответствующей точкой у

на рассчитанной кривой.

Затем смещаются на одну тЪчку вправо и вновь рассматривают три по-

следовательные точки. Легко показать, что при таком сглаживании но-

вые значения у

получаются в виде

Уг = ^{УГ~Х + Уг + У1+1)' О-Ю!)

Иногда употребляют более сложные виды сглаживания. Например, при

сглаживании многочленом третьей степени по пяти точкам выражение

для расчета нового значения у

в средней (третьей) точке запишется так:

У1

(-3+ 17Уг+ 120*+!- 3у

1+%

). (1.102)

оэ

Сглаженную функцию далее интерполируют полиномом, который

затем дифференцируют.

Интерполяционный полином находят, решая систему уравнений

У а

х^ = уг

0<1<я. (1.103)

к = 0

Иногда дифференцирование табличных функций проводят иначе.

Для первых пяти последовательных точек методом наименьших квад-

ратов находят параметры полинома второй или третьей степени и вы-

числяют производную этого полинома в средней (т. е. третьей) точке.

Потом смещаются на одну точку вправо и процедуру повторяют. Оба

12$

способа дифференцирования в принципе дают близкие результаты и

легко реализуются с помощью ЭВМ.

Численное интегрирование. Вычисление определенных интегралов

в большинстве случаев не может быть проведено аналитически. Рас-

смотрим два наиболее часто используемых метода численного расчета:

метод трапеций и метод Симпсона. Оба метода построены на примене-

нии интерполяционных формул.

В методе трапеций интегрируемую функцию интерполируют поли-

номом первой степени. Пусть на отрезке [а, Ь] задана функция у =

/ (х), принимающая на концах

значения / (а) и /(6). Если исход-

ную кривую между точками а и Ь

заменить секущей, то искомый ин-

теграл, геометрический смысл кото-

рого площадь под кривой у = / (х)

на отрезке [а, Ь], заменится площадью

трапеции (рис. 1.42). Можно записать

приближенное равенство

Рис. 1.42. Геометрическая интер-

претация интегрирования методом

трапеций

/•

(х)

йх :

— (Ь-

а)и(а) + [(Ь)).

(1.104)

членом

(1.105)

Погрешность этого приближения оценивается остаточным

где

~х

— средняя точка отрезка [а, Ь]. Поскольку длина отрезка (Ь —а)

может быть большой, точность формулы (1.104) не велика. Для увели-

чения точности число точек увеличивают а = *

< х

С ... х

= Ь,

т. е. интервал разбивают на сумму отрезков хД (рис, 1.42), для

каждого из которых применяют формулу трапеций. В результате

Ь П

А 1—1

Если длины отрезков одинаковы, т. е. х

— х^

= к, то

[^Г

(*оЖ<*^ + '•'+! (*

-1) + \! (*»)]•

•

107

)

Можно показать, что точность формулы (1.107), которая называется

формулой трапеций, оценивается остаточным членом вида

№ (Ь — а) Г (I),

(1.108)

где I — точка отрезка [а, Ь].

35$

Очевидно, что если вторая производная /"•(*) ограничена на от-

резке [а, Ь], то при к

—>

0 остаточный член стремится к нулю как № и

точность формулы (1.107) возрастает. На основании формулы для оста-

точного члена можно до проведения вычислений оценить, при каком к

будет обеспечена необходимая точность расчета интеграла по формуле

трапеций. На практике обычно этого не делают, а вначале рассчитыва-

ют приближенное значение интеграла по формуле (1.107) при неко-

тором значении к. Затем уменьшают шаг к вдвое и повторяют расчеты.

Если разница двух вычисленных значений меньше заданной точности,

то принимают результат последнего расчета за значение интеграла!

Если точность не достигнута, то шаг снова делят пополам и процеду-

ра повторяется.

Большую точность расчета при одинаковом шаге интегрирования

обеспечивает метод Симпсона, при котором вместо линейной интерпо-

ляции используют параболическую. Отрезок 1а, Ь] разбивают на чет-

ное число отрезков и через каждые три последовательные точки прово-

дят параболу. Легко показать, что окончательная формула для чис-

ленного расчета интеграла на равномерной сетке (х

— = к)

будет иметь вид

/ (х) йх

[/(*о) + 4/ (х

) + 2/ (*,) + 4/ (*,) + . .. +

+ 2

(х

)

4Г

(Хп-

) И (*п)]•

Остаточный член имеет вид

№

180

(1.109)

(1.110)

где | принадлежит [а, Ь]. Формула (1.110) показывает, что с уменьше-

нием/1 величина # быстрее стремится к нулю, чем в формуле трапеций.

В табл. 1.6 сопостав-

Таблица 1,6. Сопоставление результатов

двух методов численного интегрирования

лены результаты расче-

та интеграла

Ах «

^ 4,3281 этими метода-

ми при одинаковых к.

Заметим, что если

функция задана таблич-

но, то ее перед интегри-

рованием либо аппрок-

симируют полиномом,

либо сглаживают, а за-

тем используют метод трапеций или Симпсона. Число точек, которые

разбивают отрезок при интегрировании по методу Симпсона, должно

быть нечетным.

Метод

трапеций \ Симпсона

2,0

5,0000

1,0

4,5000

4,3333

0,5

4,3713

4,3284

0,25

4,3389

4,3281

Численное

решение уравнений. На практике многие алгебраические

и трансцендентные уравнения не могут быть решены аналитически.

Существует довольно многр приемов численного решения данной зада-

чи. Рассмотрим некоторые из них.

Пусть имеется непрерывная функция

У = Г(х),

(1.111)

у которой на отрезке [а, Ь] существует единственный корень

Ш)=0, (1.112)

который требуется найти с точностью е.

Положим для определенности, что у = ! (х) является возрастающей

функцией и, таким образом, / (а) С 0, /

(Ь)

> 0. Решить данную зада-

чу — значит найти такое значение х, для которого \х — | [ < е.

В методе половинного деления (дихотомии) поступают так. Рас-

считывают координату середины отрезка [а, Ь] с = (а + Ь) 12. Вычис-

ляют функцию / (с) в этой точке. Если / (с) > 0, то ясно, что корень

находится между а и с. Если / (с) < 0, то корень расположен между

точками с и

Ъ.

После выяснения, на каком из отрезков [а, с] или [с, Ь]

находится корень уравнения, половину, не содержащую корень, отбра-

сывают, а к другой, содержащей корень, применяют тот же метод поло-

винного деления и т. д. После п операций деления пополам длина от-

резка, содержащего корень, станет (Ь — а)12

и будет выполнено не-

равенство (Ь — а)/2

< е. Это означает, что любая точка полученного

отрезка будет отстоять от I на расстоянии, меньшем или равном е, и,

например, его середину можно принять за приближенное значение*

корня.

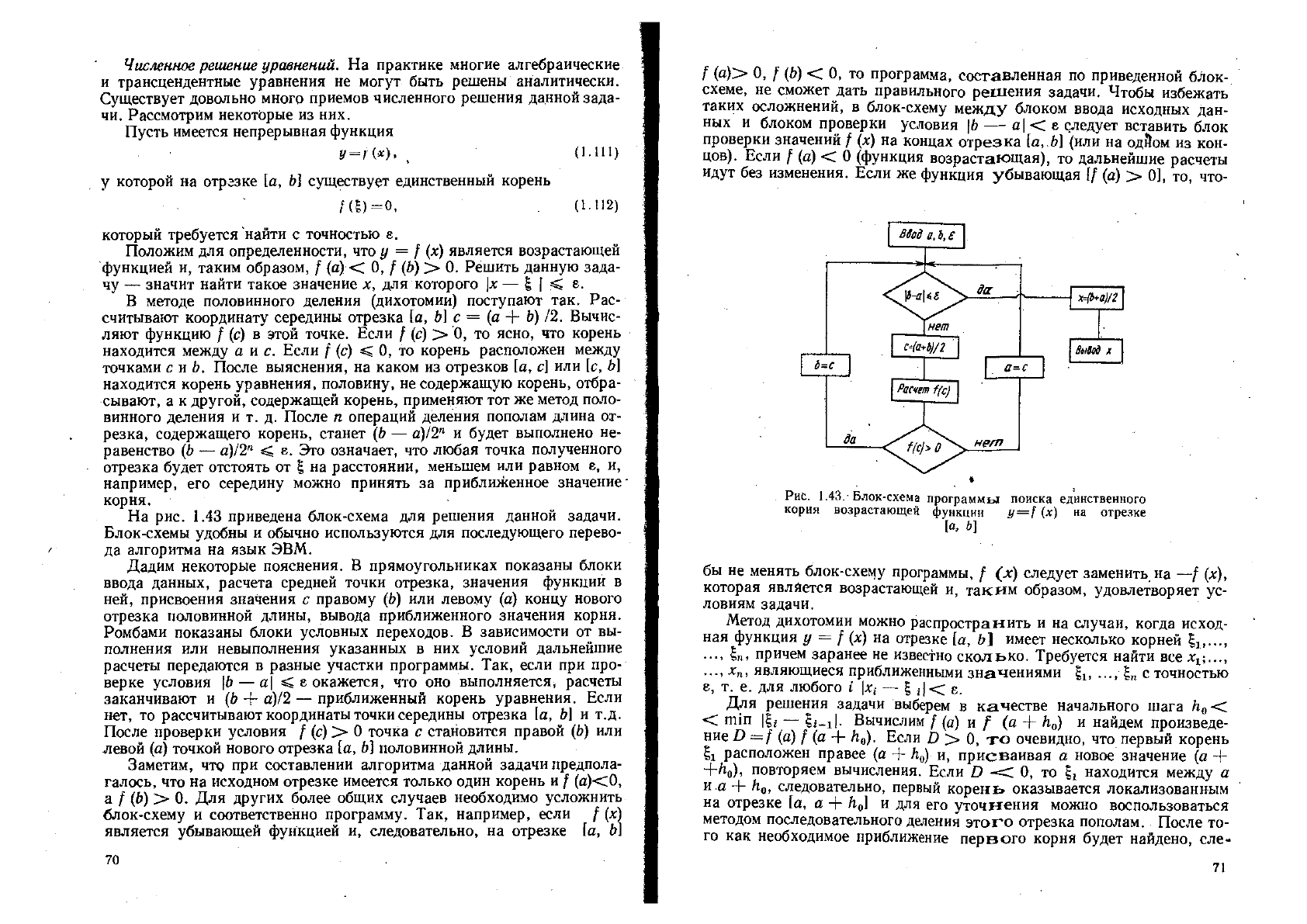
На рис. 1.43 приведена блок-схема для решения данной задачи.

Блок-схемы удобны и обычно используются для последующего перево-

/ да алгоритма на язык ЭВМ.

Дадим некоторые пояснения. В прямоугольниках показаны блоки

ввода данных, расчета средней точки отрезка, значения функции в

ней, присвоения значения с правому (Ь) или левому (а) концу нового

отрезка половинной длины, вывода приближенного значения корня.

Ромбами показаны блоки условных переходов» В зависимости от вы-

полнения цли невыполнения указанных в них условий дальнейшие

расчеты передаются в разные участки программы. Так, если при про-

верке условия |Ь — а\ < е окажется, что оно выполняется* расчеты

заканчивают и (Ь + а)/2 — приближенный корень уравнения. Если

нет, то рассчитывают координаты точки середины отрезка [а, Ь] и т.д .

После проверки условия / (с) > 0 точка с становится правой (Ь) или

левой (а) точкой нового отрезка [а, Ь] половинной длины.

Заметим, что при составлении алгоритма данной задачи предпола-

галось, что на исходном отрезке имеется только один корень и / (а)<0,

а /

(Ь)

> 0. Для других более общих случаев необходимо усложнить

блок-схему и соответственно программу. Так, например, если / (х)

является убывающей функцией и, следовательно, на отрезке [а, Ь]

! (а)> 0, /

(Ь)

< 0, то программа, составленная по приведенной блок-

схеме, не сможет дать правильного решения задачи. Чтобы избежать

таких осложнений, в блок-схему между блоком ввода исходных дан-

ных и блоком проверки условия

\Ь

— а\ < е следует вставить блок

проверки значений / (х) на концах отрезка

[а,.Ь]

"(или на одйом из кон-

цов). Если / (а) < 0 (функция возрастающая), то дальнейшие расчеты

идут без изменения. Если же функция убывающая [/ (а) > 0], то, что-

Вбод а,Ь,

хф+а)/2

\нет

с=(а+Ь)/2

8ыбод

6= с а=с

да .

Расчет-Г(с)

Рис. 1.43. Блок-схема программы: поиска единственного

корня возрастающей функции */=/ (*) на отрезке

[а, Ь]

бы не менять блок-схе^у программы, / (х) следует заменить на —/ (*),

которая явлйется возрастающей и, таким образом, удовлетворяет ус-

ловиям задачи.

Метод дихотомии можно распространить и на случаи, когда исход-

ная функция у = / (х) на отрезке [а, Ь] имеет несколько корней

..., Ъ

пу

причем заранее не известно сколько. Требуется найти все

..., х

П1

являющиеся приближенными значениями ..., |

с точностью

е, т. е. для любого I

\х%

— ! < е.

Для решения задачи выберем в качестве начального шага /1

<С

< пип — ||_х|.. Вычислим / (а) и р (а + Н

) и найдем произведе-

ние О =/ (а) / (а + Н

). Если Ь > 0, то очевидно, что первый корень

^ расположен правее (а +

)

и, присваивая а новое значение (а +

+й

), повторяем вычисления. Если О С 0, то находится между а

и а + /г

, следовательно, первый корень оказывается локализованным

на отрезке 1а, а + Н

] и для его уточнения можно воспользоваться

методом последовательного деления этого отрезка пополам. После то-

го как необходимое приближение первого корня будет найдено, еле-

324 12$

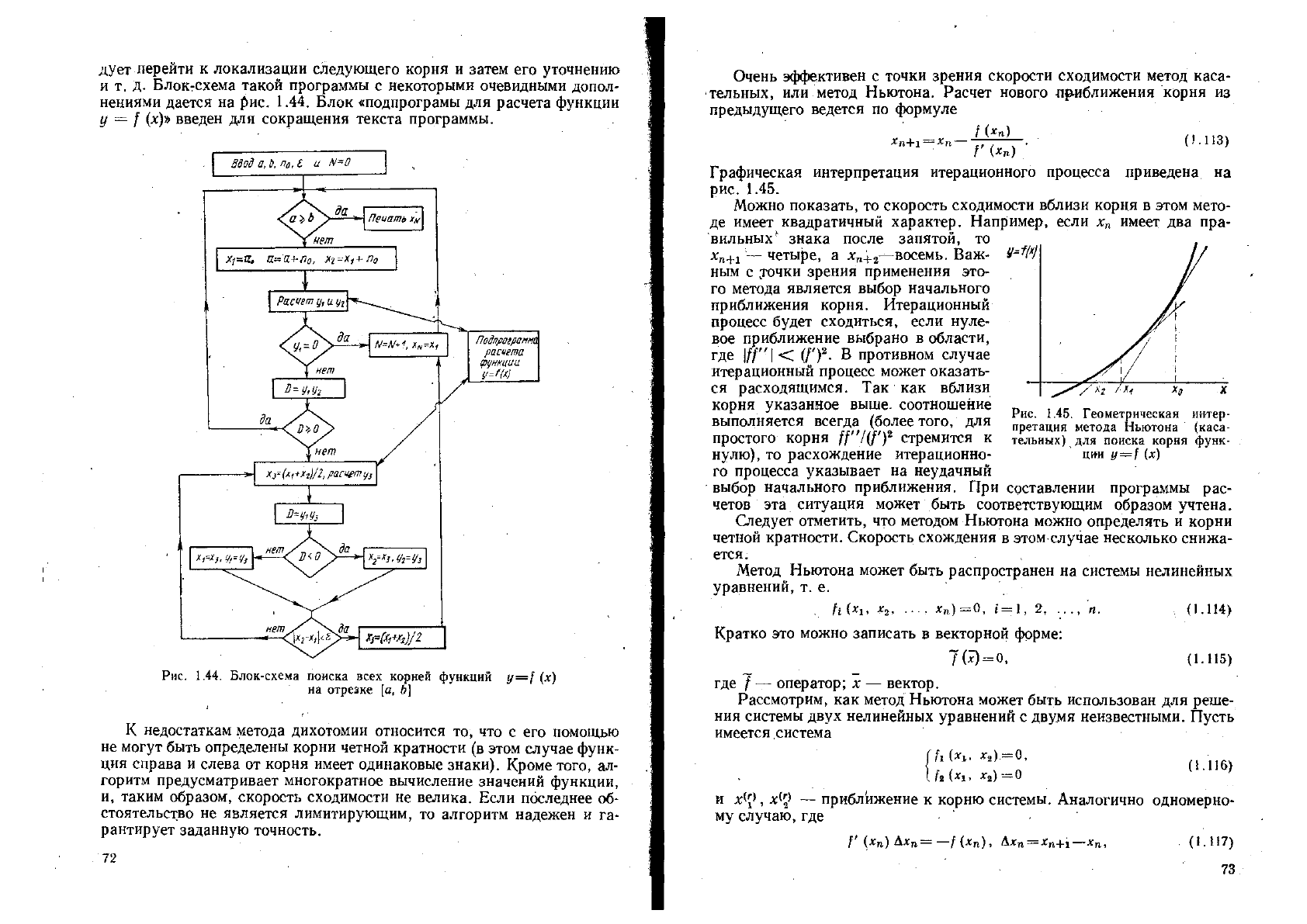
дует перейти к локализации следующего корня и затем его уточнению

и т. Д. Блокгсхема такой программы с некоторыми очевидными допол-

нениями дается на рис. 1.44. Блок «подпрограмы для расчета функции

У = / ОФ введен для сокращения текста программы.

Ввод а, Ь,

, е а N-0

Печать хы

ТШ77

Рис. 1.44. Блок-схема поиска всех корней функций у-

на отрезке [а, Ь]

-I (х)

К недостаткам метода дихотомии относится то, что с его помощью

не могут быть определены корни четной кратности (в этом случае функ-

ция справа и слева от корня имеет одинаковые знаки). Кроме того, ал-

горитм предусматривает многократное вычисление значений функции,

и, таким образом, скорость сходимости не велика. Если последнее об-

стоятельство не является лимитирующим, то алгоритм надежен и га-

рантирует заданную точность.

37$

Очень эффективен с точки зрения скорости сходимости метод каса-

тельных, или метод Ньютона. Расчет нового приближения корня из

предыдущего ведется по формуле

П*п)

ХП+Г^ХП -

(1.113)

приведена на

Г (х

)

Графическая интерпретация итерационного процесса

рис. 1.45.

Можно показать, то скорость сходимости вблизи корня в этом мето-

де имеет квадратичный характер. Например, если х

имеет два пра-

вильных' знака после запятой, то

1 — четыре, а восемь. Важ-

ным с ,точки зрения применения это-

го метода является выбор начального

приближения корня. Итерационный

процесс будет сходиться, если нуле-

вое приближение выбрано в области,

где |//'|< (Г)

- В противном случае

итерационный процесс может оказать-

ся расходящимся. Так как вблизи

корня указанное выше, соотношение

выполняется всегда (более того, для

простого корня //"/(/')* стремится к

нулю), то расхождение итерационно-

го процесса указывает на неудачный

выбор начального приближения. При составлении программы рас-

четов эта ситуация может быть соответствующим образом учтена.

Следует отметить, что методом Ньютона можно определять и корни

четной кратности. Скорость схождения в этом случае несколько снижа-

ется.

Метод Ньютона может быть распространен на системы нелинейных

уравнений, т. е.

, М*!, ...» *п)=0,

= 1, 2, п.

(1.114)

Кратко это можно записать в векторной форме:

1(х) = 0, (1.115)

где [ — оператор; х — вектор.

Рассмотрим, как метод Ньютона может быть использован для реше-

ния системы двух нелинейных уравнений с двумя неизвестными. Пусть

имеется система

Рис. 1.45. Геометрическая интер-

претация метода Ньютона (каса-

тельных) для поиска корня функ-

ции (х)

(1.П6)

/г х

)=0,

Ы*1> Х

) --=0

и х^, — приближение к корню системы. Аналогично одномерно-

му случаю, где

/' (*п)А*п=— Нхп), кхп^хп+г—хп, (1.117)

123

получим систему двух линейных уравнений с двумя неизвестными;

К>, *<") Л- И", 4") А4" = -ЛИ". 4"),

М лг (Ы18)

Вычислив неизвестные АхЧ? и Ддг<{>, легко рассчитать новые прибли-

жения и

• х\'+»±Х1'> + АХ\'\ (1.119)

г+1)

г)

+Ах</> и Т.д. (1.120)

Как и в одномерном случае, метод Ньютона сходится очень быстро

(во многих случаях за 3—5 итераций) и поэтому часто применяется

на практике.

Определенным недостатком метода Ньютона является необходи-

мость вычисления одновременно со значением функции и ее производ-

ной. Этого недостатка лишен метод «секущих», в котором вместо фор-

мулы (1.113) используется итерационная формула

(К121)

где* (д^) [/• — / (Лп-

)]/ (ж^

Правда, сходимость метода секущих более медленная — линейная.

В заключение необходимо отметить, что изложенный здесь матери-

ал охватывает, на наш взгляд, наиболее часто встречающиеся на прак-

тике вопросы, связанные с обработкой экспериментальных данных.

Подходы к решению задач, которые не нашли своего отражения в дан-

ном разделе, можно найти в специальной литературе.

Глава 2

РАСТВОРЫ ЭЛЕКТРОЛИТОВ

И ЭЛЕКТРОХИМИЧЕСКИЕ ЦЕПИ

#Теоретические основы

# Изменение электропроводности растворов электролитов

# Изменение ЭДС электрохимических цепей

§ 2.1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ

Электрохимическая цепь представляет собой систему, состоящую

из последовательно соединенных проводников первого и второго рода.

Проводниками первого рода могут быть металлы и полупроводники, а

проводниками второго рода — растворы электролитов, их расплавы,

а также твердые электролиты. Мщ ограничимся рассмотрением элект-

рохимических цепей, построенных из металлов и растворов электро-

литов.

Как показывают термодинамические и модельные расчеты, энергия

взаимодействия катионов и анионов с дипольными молекулами раст-

ворителя (энергия сольватации) во многих случаях оказывается доста-

точной для того, чтобы компенсировать энергию электростатического

взаимодействия ионов в ионных кристаллах (энергию кристалличе-

ской решетки) или энергию ковалентной связи атомов в таких молеку-

лах, как НС1 или НВг. В результате растворы электролитов являются

, устойчивыми ионными системами, содержащими сольватированные ка-

тионы и анионы.

В бесконечно разбавленных растворах расстояние между ионами

становится настолько большим, что взаимодействие ионов друг с дру-

гом стремится к нулю. По мере уменьшения этого расстояния с повы-

шением концентрации электролита прежде всего проявляется элект-

ростатическое притяжение ионов противоположного знака и отталки-

вание ионов, имеющих одинаковый знак заряда. Следствием этого яв-

ляется отклонение растворов электролитов от идеальности при кон-

центрациях, существенно более низких по сравнению с растворами не-

электролитов.

Важной особенностью растворов электролитов является то, что

экспериментально невозможно определить, активность или коэффици-

соот™ия-

И 0ТДеЛЬН0Г0 вида ион

хотя

формально и записывают

а<У=*_/_

:в

<«>^

у+

<«)

= л|

> (21)

где а<? и

(-> - активности ионов соответственно в шкале молярно-

™

ЛЬНОСТ6Й; и

~ отвечающие этим шкалам коэффициенты

активности; с

да, - молярная и моляльная концентоаыиГионпп /

Предполагают, что химический потенциал шолекульГсолиД оаствоое

ставляквдих ГГнГ^^^

И3 ХИМИЧескИХ

« Г

™

66 И0Н0В

При этом

условии получают следующую форму-

лу, связывающую определяемую из опыта активность Ц А с

активностями катионов и анионов Л

соли ^ а+

, (2.2)

где V/ — стехиометрические числа. Учитывая соотношения (2 П я

Г-7Г„ли

еНТРа

И0Н0В С 061466 концен

трацией элек^)ол'ита

(Ъ-ч^ти т^пт), уравнение (2.2) можно переписать в виде

= V-

или

<«>_^

+ (2 3)

не

НЯТИеМ

ак

™вность соли» в электрохимии обычно

не. пользуются. Вместо этого вводят понятия средней активно

сти и среднего коэффициента активности: средней активно-

му^; =

Из формул (2.3) и (2.4) следует, что

Я (2.5)

где I = — коэффициент, зависящий от валентного типа

электролита. -

ДЛЯ рас

°р°

электролитов, как правило,

" п моляльностей, т. е. дают величины

т±

„ри раз-

^мульГ

ДЛЯ Пер6Х0Да К ШКаЛ6 мога

««* используют следуюпще

^гпр/О + 0№тМ

сош

)

(2б)

/^Т^Ро^/с, (2.7)

где р и р

— плотность раствора и растворителя соответственно* М

ШССа С0ЛИ

Из

УР«Й (2.5) и (2.7) следует^ °что

пл

определения активности растворов электролитов можно ис-

н^пяп

Т6 Же методы

что й для

растворов неэлектролитов (давле-

ние пара над раствором, осмотическое давление раствора, его тапер*

ПРИ ТаК0М

определени

и^начале ?ол.

ностью игнорируют образование ионов в растворе и для каждой кон-

39$

центрации находят а<^

ли

или а^ли- После этого с учетом образования

из каждой «молекулы соли» ионов по формулам (2,4) находят или

а по формулам (2.5)—коэффициенты активности /± или у

. Равно-

весные свойсша электрохимических цепей лежат в основе еще одного

чисто электрохимического метода определения активности растворов

электролитов. Чтобы познакомиться с этим методом, необходимо ввести

одно из фундаментальных понятий электрохимии -^понятие электро-

химического потенциала.

Электрохимический потенциал частицы I в фазе а равен ум-

ноженной на число Авогадро работе перенесения этой частицы из бес-

конечно удаленной точки в вакууме внутрь фазы ои Вспомним, что

электрохимический потенциал точки внутри фазы а (внутренний по-

тенциал этой фазы — ф«*>) определяется аналогичной работой перено-

са, но не реальной частицы *, а единицы воображаемого заряда. По-

этому можно записать

где,

— заряд частицы г с учетом знака; е

— 1,602-10^

Кл — эле-

ментарный заряд; Л^д = 6,022-10

— число Авогадро; Р = е

N а =

— 96485 Кл/г-экв — число Фарадея. Входящая в формулу (2.8)

неэлектростатическая составляющая электрохимического потен-

циала представляет собой химический потенциал частицы I в

фазе а. В самом деле, для незаряженной частицы = 0 и р

— а физический смысл становится идентичен физическому

смыслу химического потенциала.

На практике можно определить лишь работу переноса реально за*

ряженных частиц, т. е. Д|л*, а не воображаемых единичных зарядов.

Но, как следует из уравнения (2.8), Дщ = только при усло-

вии, что начальное и конечное состояния имеют одинаковый химиче-

ский потенциал. Иначе говоря, электрическую разность потенциалов

Дф между двумя точками можно экспериментально измерить лишь

в том случае, если эти точки расположены в одинаковых по составу

фазах. Наоборот, если точки расположены в различных по химическо-

му составу фазах а и 0, то возникающую между ними электрическую

разность потенциалов Д«ф — ф

(Р)

—

<р<®>

(так называемый гальвани-

потенциал) измерить невозможно. Поэтому измеряемая на концах

электрохимической цепи разность потенциалов отвечает такой цепи, ко-

торая заканчивается идентичными металлами (рис. 2.1, а).

Практически, однако, используют цепи (рис. 2.1, б), в которых к

двум различным металлам М1 и М2 подключают медные провода. Но

это не изменяет существа дела, поскольку цепи а и б (рис. 2.1) эквива-

лентны. В самом деле, согласно закону Вольта, включение между дву-

мя металлами Си и М2 металлического проводника М1 не изменяет

разность потенциалов на концах цепи, т, е. цепи бив(рис.2.1)эквива-

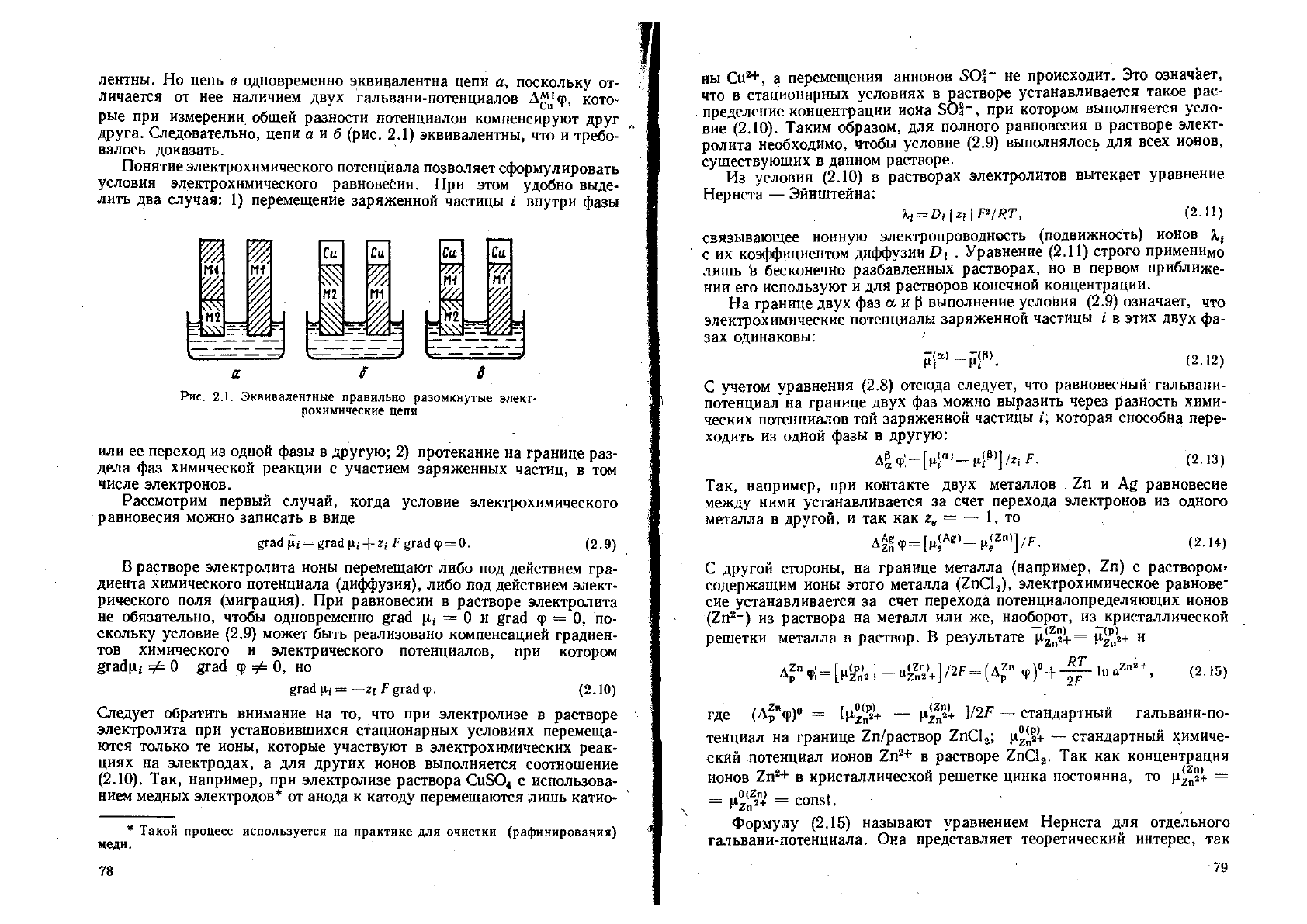
лентны. Но цепь б одновременно эквивалентна цепи а, поскольку от-

личается от нее наличием двух гальвани-потейциалов А^Ф, кото-

рые при измерении общей разности потенциалов компенсируют друг

друга. Следовательно, цепи а и б (рис. 2.1) эквивалентны, что и требо-

валось доказать.

Понятие электрохимического потенциала позволяет сформул ировать

условия электрохимического равновесия. При этом удобно выде-

лить два случая: 1) перемещение заряженной частицы г внутри фазы

Си

911

иш

Си

Рис. 2.1. Эквивалентные правильно разомкнутые элект-

рохимические цепи

или ее переход из одной фазы в другую; 2) протекание на границе раз-

дела фаз химической реакции с участием заряженных частиц, в том

числе электронов.

Рассмотрим первый случай, когда условие электрохимического

равновесия можно записать в виде

§гас1{Г* = ^гас!

ц*

+ Р

<р

= 0. (2.9)

В растворе электролита ионы перемещают либо под действием гра-

диента химического потенциала (диффузия), либо под действием элект-

рического поля (миграция). При равновесии в растворе электролита

не обязательно, чтобы одновременно = 0 и §гас! <р = 0, по-

скольку условие (2.9) может быть реализовано компенсацией градиен-

тов химического и электрического потенциалов, при котором

дгайр* Ф 0 б

ай ф ф 0, но

§гас! = —гг Р $гайц). (2.10)

Следует обратить внимание на то, что при электролизе в растворе

электролита при установившихся стационарных условиях перемеща-

ются только те ионы, которые участвуют в электрохимических реак-

циях на электродах, а для других ионов выполняется соотношение

(2.10). Так, например, при электролизе раствора Си30

с использова-

нием медных электродов* от анода к катоду перемещаются лишь катио-

* Такой процесс используется на практике для очистки (рафинирования)

меди.

40 12$

ны Си

*, а перемещения анионов 501 ~ не происходит. Это означает,

что в стационарных условиях в растворе устанавливается такое рас-

пределение концентрации иона 502~, при котором выполняется усло-

вие (2.10). Таким образом, для полного равновесия в растворе элект-

ролита необходимо, чтобы условие (2.9) выполнялось для всех ионов,

существующих в данном растворе.

Из условия (2.10) в растворах электролитов вытекает уравнение

Нернста — Эйнштейна:

— р« |

аг«

| /*/*7\ (2.И)

связывающее ионную электропроводность (подвижность) ионов Х

с их коэффициентом диффузии . Уравнение (2.11) строго применимо

лишь 'в бесконечно разбавленных растворах, но в первом приближе-

нии его используют и для растворов конечной концентрации.

На границе двух фаз а и Р выполнение условия (2.9) означает, что

электрохимические потенциалы заряженной частицы л в этих двух фа-

зах одинаковы:

= (2.12)

С учетом уравнения (2,8) отсюда следует, что равновесный гальвани-

потенциал на границе двух фаз можно выразить через разность хими-

ческих потенциалов той заряженной частицы которая способна пере-

ходить из одной фазы в другую:

Так, например, при контакте двух металлов 2п и А§ равновесие

между ними устанавливается за счет перехода электронов из одного

металла в другой, и так как г

= — 1, то

АЙФ»!^-^]/^. (2.14)

С другой стороны, на границе металла (например, 2п) с раствором»

содержащим ионы этого металла (2пС1

), электрохимическое равнове"

сие устанавливается за счет перехода потенциалопределяющих ионов

(2п

~) из раствора на металл или же, наоборот, из_кристаллической

решетки металла в раствор. В результате ^2+= и

, (2.15)

где (Ар

ф)° = [^

(

2+ — 1/2 Р — стандартный гальвани-по-

тенциал на границе 2п/раствор 2пС1

; ^„И — стандартный химиче-

ский потенциал ионов 2п

в растворе 2пС1

. Так как концентрация

ионов 2п

в кристаллической решетке цинка постоянна, то =

= « СОПЗ*.

Формулу (2.15) называют уравнением Нернста для отдельного

гальвани-потенциала. Она представляет теоретический интерес, так

101