Дамаскин Б.Б., Петрий О.А., Подловченко Б.И. и др. Практикум по электрохимии

Подождите немного. Документ загружается.

Снимают зависимость^ отв растворах: 0,ШНС1 + ШКВг; О,Ш

НС1 + Ю-

[(С

)

Шг и 0.1М НС1; электроды — Не, Вг, РЪ.

Построить график и объяснить полученные данные.

§ 4.5. ИМПЕДАНСНЫЙ МЕТОД ИЗУЧЕНИЯ

ЭЛЕКТРОХИМИЧЕСКОЙ КИНЕТИКИ

Общая характеристика релаксационных методов. Как следует т

теории многостадийных электродных процессов, кинетику стадии

разряда—ионизации можно изучить лишь при условии, что измеряемая

константа скорости этой стадии &<

> значительно меньше, чем диф-

фузионная константа скорости ^ последовательно протекающей ста-

дии массопереноса:

й<

изм

> << 6

Г)

« 0/6

эф

, (4.70)

где О — коэффициент диффузии реагирующей частицы; б

эф

— эф-

фективная толщина диффузионного слоя.

В полярографическом методе, как следует из уравнения (4,33),

5э

Ф ^ У^Ри а потому при = и О = 10~

см

/с, к

~ 1А0-

/(3,14 • 3) « 10~

см/с. В методе вращающегося диско-

вого электрода согласно формуле (4.60) при й ==. 10~

см

/с и угловой

скорости вращения 1000 об/мин, когда со = 2л 1000/60 ~ 105 рад/с;

эф

- 1,61 • (10-

)

/з(0,01)

/6/ю5

= 1>6

. 1<)-»смЧ, следовательно,

ко « 6,3 • Ю-

см/с. Наконец, при- снятии стационарных поляриза-

ционных кривых на неподвижном электроде толщина диффузионного

слоя по порядку величины равна радиусу электрода [см. второе слагае-

мое в правой части уравнения (4.33)1, а потому при б

эф

« 0,5 см и

В = 10~

см

/с « 2 • 10"*

.см/с*. Таким образом, описанные в

предыдущих параграфах методы позволяют исследовать кинетику

стадии разряда—ионизации для сравнительно медленных электродных

процессов, у которых 6<

изм

> < 10~

ч- 10~

см/с.

Для изучения более быстрых электрохимических реакций исполь-

зуют так называемые релаксационные методы, обеспечивающиесущест-

венно большие значения ко. Достигается это за счет резкого уменьше-

ния времени, через которое регистрируют состояние системы после

вывода ее из равновесного состояния. Физический смысл таких изме-

рений заключается в том, что за очень малые промежутки времени при-

мыкающий к злектроду слой раствора не успевает существенно обед-

ниться реагирующим веществом, а потому стадия массопереноса как

* В результате естественной конвекции 6

ф может на порядок уменьшиться,

а константа к

соответственно возрасти.

192

бы утрачивает свое значение. Формально же получается, что при /

_>- о б

эф

0, а к

->- оо и оо [см. уравнение (4.

33)], т. е. лимити-

рующей становится стадия разряда—ионизации.

Релаксационные методы условно делят на три группы: 1) импульс-

ные потенциостатические; 2) импульсные гальваностатические; 3) ме-

тоды, основанные на использовании переменного тока. В первой груп-

пе методов систему выводят из равновесия за счет заданного изменения

потенциала и регистрируют зависимость тока от времени. Во второй

группе, наоборот, систему выводят из равновесия за счет пропускания

запрограммированного тока, а регистрируют зависимость потенциала

от времени. Наконец, методы третьей группы основаны йа периоди-

ческих колебаниях исследуемой системы около ее равновесного со-

стояния. Именно к этой группе относится импедансный метод, сущ-

ность которого заключается в измерении общего сопротивления элект-

рохимической системы (ее импеданса) при протекании через нее си-

нусоидального переменного тока.

Отметим, что использование релаксационных методов для изуче-

ния стадии разряда—ионизации быстрых электрохимических реак-

ций [типа реакции может дать непротиворечивые результаты

только при условии, если реагирующие вещества Ох и Нес! специфи-

чески не адсорбируются на исследуемом электроде и, следовательно,

выполняется соотношение (4.5).

Импеданс электрохимической реакции (А) при учете стадии раз-

ряда—ионизации

диффузии реагирующих частиц. Предположим, что

вещества Ох и Ней специфически не адсорбируются на исследуемом

электроде, а их концентрация существенно меньше концентрации

электролита фона и, следовательно, введение в раствор Ох и Кед не

сказывается на общем сопротивлении раствора #

-р

и емкости двой-

ного электрического слоя с

. Предположим также, что площадь ис-

следуемого электрода существенно (более чем в 100 раз) меньше пло-

щади вспомогательного электрода, т. е. вкладом последнего в общий

измеряемый импеданс можно пренебречь. В этих условиях электрохи-

мическая ячейка оказывает переменному синусоидальному току ма-

лой амплитуды такое же сопротивление, как и эквивалентная элект-

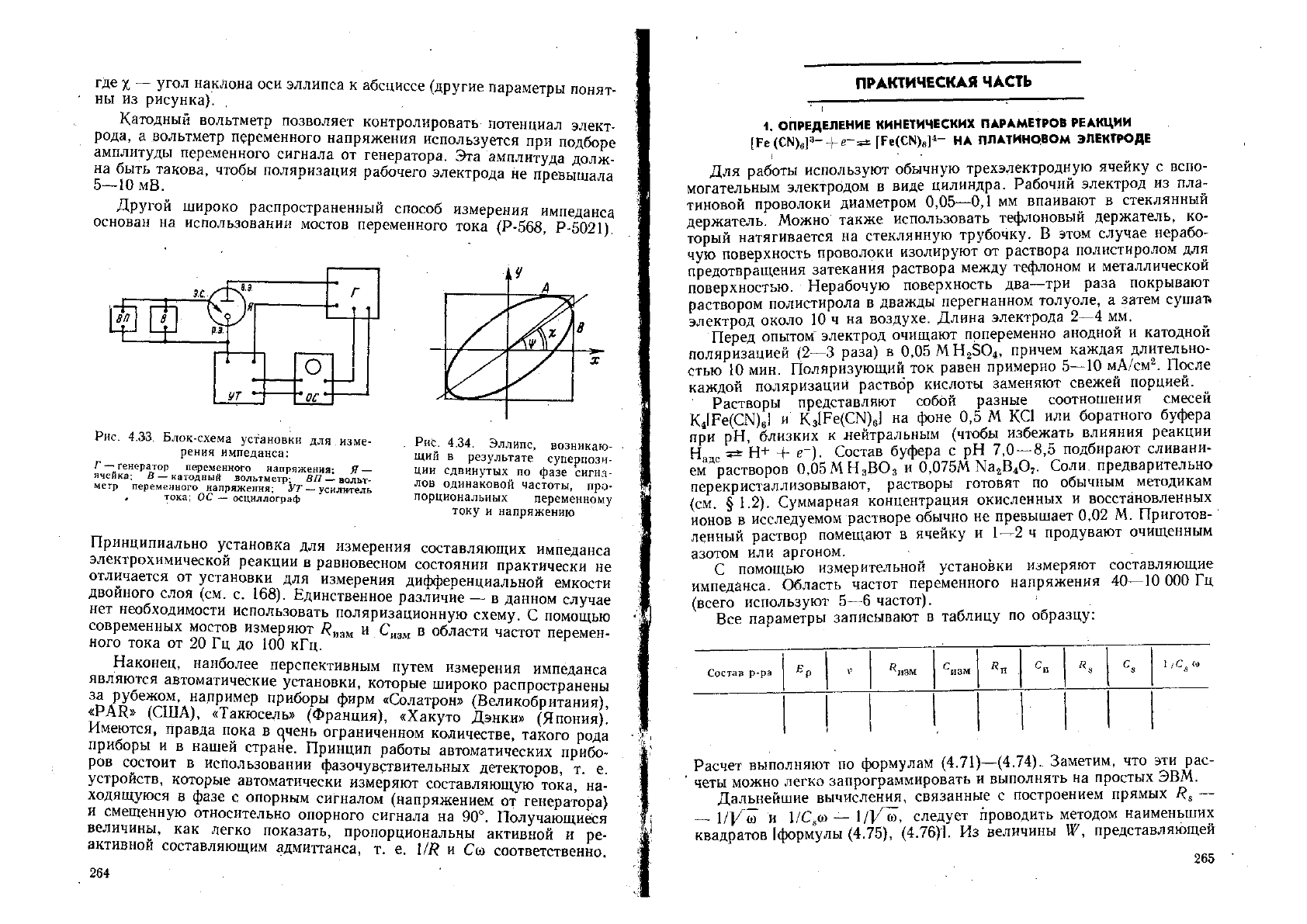
рическая схема, представленная на рис. 4.31. Изображенные на этой

схеме и зависящие от частоты переменного тока со = 2ПУ емкость

(со) и сопротивление К

(со) моделируют импеданс фарадеевского

процесса.

Чтобы получить интересующие нас величины и С

из эксперимен-

тально измеряемых #

изм

и С

изм

, характеризующих общий импе-

данс схемы 4.31, поступают следующим образом. Вначале измеряют

импеданс в чистом растворе фона. В этих условиях #изм = #

и Сязм'—Сд.

. Знание /?р.

ра

и С

позволяет из опытных величин

#взм и

иш

растворе, содержащем Ох и К её, рассчитать /?

8У

используя следующие формулы:

#п= (#изм— #р-ра) га ' (4*71)

7 Зак. 434 193

(4.72)

где \ = (/?

изм

— /?р.ра)С

изм

со и далее

п Дп

^ = + (4.74)

где = С

со и со = 2лд?—круговая частота переменного тока.

Входящие в уравнение (4.71)—(4.74) промежуточные величины и

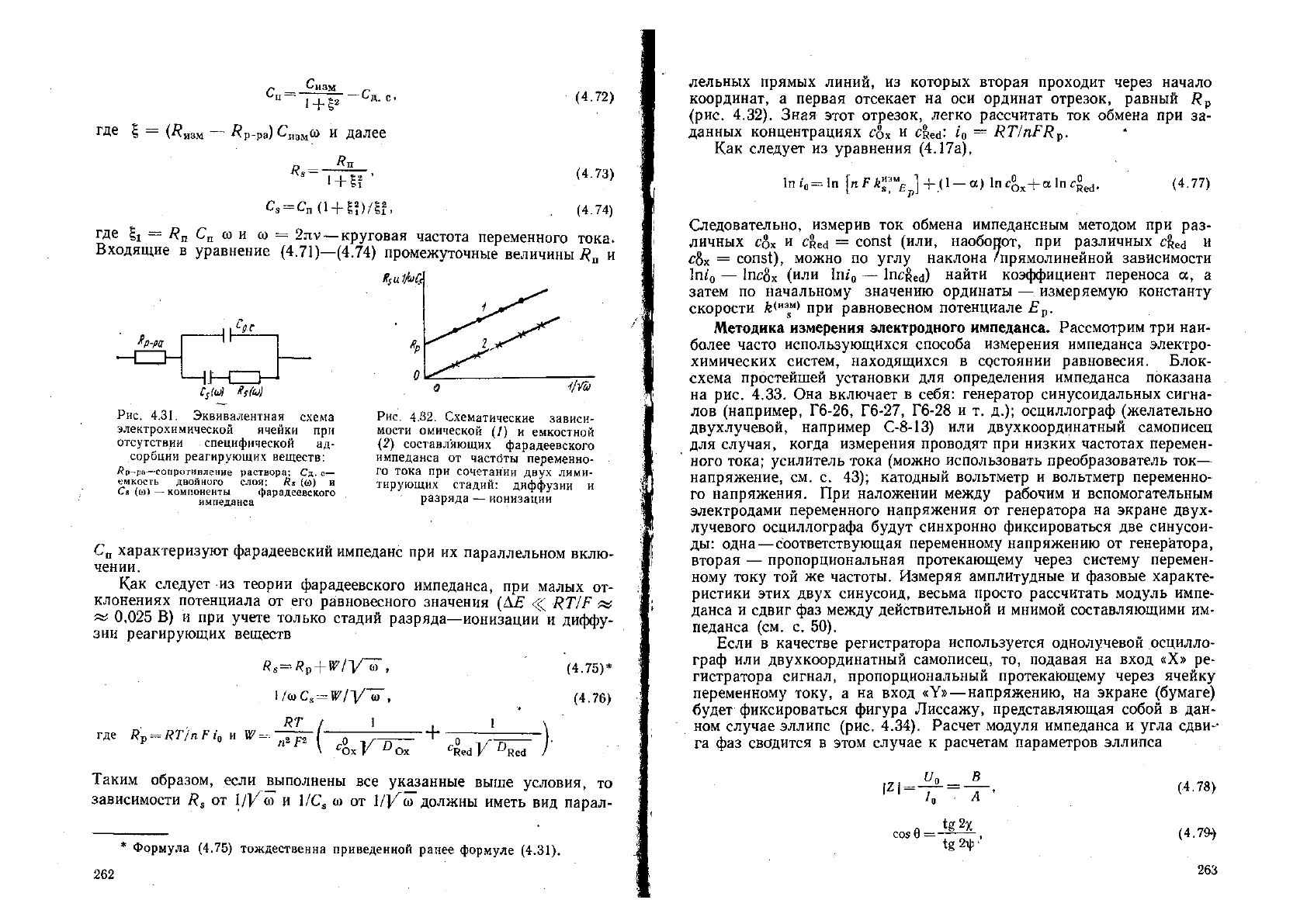
Рис. 4.32. Схематические зависи-

мости омической (/) и емкостной

(2) составляющих фарадеевского

импеданса от частбты переменно-

го тока при сочетании двух лими-

тирующих стадий: диффузии и

разряда — ионизации

характеризуют фарадеевский импеданс при их параллельном вклю-

чении.

Как следует из теории фарадеевского импеданса, при малых от-

клонениях потенциала от его равновесного значения (АЕ < ЯТ1Р «

~ 0,025 В) и при учете только стадий разряда—ионизации и диффу-

зии реагирующих веществ

= • ' (4,75)*

1/©С

= 1Г/У"ю", (4.76)

ЯТ I 1 1 ч

где Яр = ЯТ/п Р1

и -

Ох V Ох

Яе& V

Яе<1 1

Таким образом, если выполнены все указанные выше условия, то

зависимости от 1/|/(о и МС

со от НУ"® должны иметь вид парал-

* Формула (4.75) тождественна приведенной ранее формуле (4.31).

192

лельных прямых линий, из которых вторая проходит через начало

координат, а первая отсекает на оси ординат отрезок, равный

(рис. 4.32). Зная этот отрезок, легко рассчитать ток обмена при за-

данных концентрациях сбх и с^: = НТ/пРЯ

Как следует из уравнения (4.17а),

1пА»=1п {пГк"™

Ер

] + (\~-а) \п с

Ох

+а

1п

(4.77)

Следовательно, измерив ток обмена импедансным методом при раз-

личных С&х И = сопз! (ИЛИ, На0б0«0Т, При различных свей И

с&х = сопз!), можно по углу наклона /прямолинейной зависимости

1ш

— 1псох (или 1т

— 1п^ес|) найти коэффициент переноса а, а

затем по начальному значению ординаты — измеряемую константу

скорости 6<

И3

> при равновесном потенциале Е

Методика измерения электродного импеданса. Рассмотрим три наи-

более часто использующихся способа измерения импеданса электро-

химических систем, находящихся в состоянии равновесия. Блок-

схема простейшей установки для определения импеданса показана

на рис. 4.33. Она включает в себя: генератор синусоидальных сигна-

лов (например, Г6-26, Г6-27, Г6-28 и т. д.); осциллограф (желательно

двухлучевой, например С-8-13) или двухкоординатный самописец

для случая, когда измерения проводят при низких частотах перемен-

ного тока; усилитель тока (можно использовать преобразователь ток-

напряжение, см. с. 43); катодный вольтметр и вольтметр переменно-

го напряжения. При наложении между рабочим и вспомогательным

электродами переменного напряжения от генератора на экране двух-

лучевого осциллографа будут синхронно фиксироваться две синусои-

ды: одна—соответствующая переменному напряжению от генератора,

вторая — пропорциональная протекающему через систему перемен-

ному току той же частоты. Измеряя амплитудные и фазовые характе-

ристики этих двух синусоид, весьма просто рассчитать модуль импе-

данса и сдвиг фаз между действительной и мнимой составляющими им-

педанса (см. с. 50).

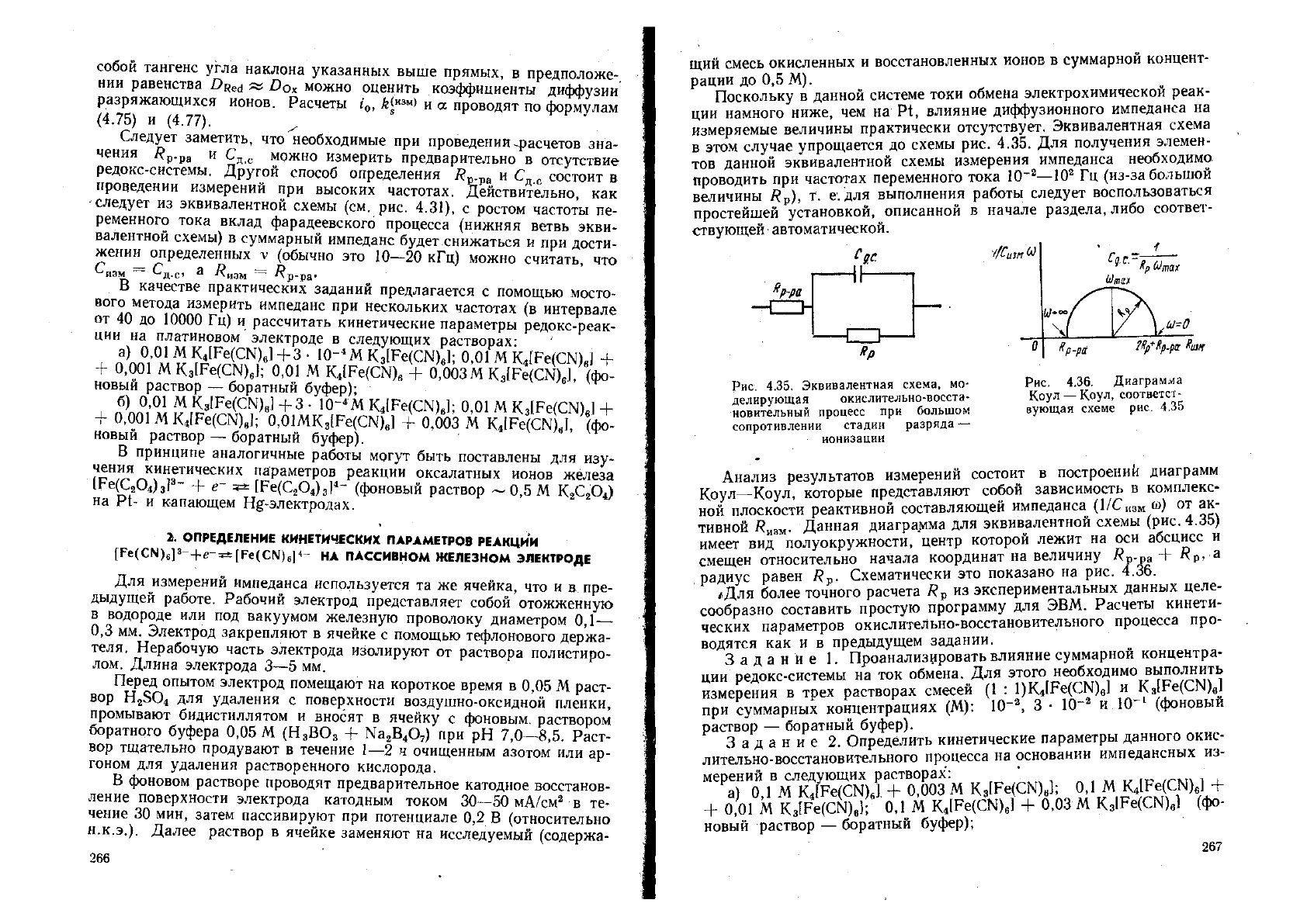
Если в качестве регистратора используется однолучевой осцилло-

граф или двухкоординатный самописец, то, подавая на вход «X» ре-

гистратора сигнал, пропорциональный протекающему через ячейку

переменному току, а на вход «V»—напряжению, на экране (бумаге)

будет фиксироваться фигура Лиссажу, представляющая собой в дан-

ном случае эллипс (рис. 4.34). Расчет модуля импеданса и угла сдви-

га фаз сводится в этом случае к расчетам параметров эллипса

^о в

= —/ (4.78)

(4.79*

7 Зак. 434 193

Рис. 4.31. Эквивалентная схема

электрохимической ячейки при

отсутствии специфической ад-

сорбции реагирующих веществ;

/?р-ра—сопротивление раствора; Сд. с—

емкость двойного слоя; (со) и

С» (о) — компоненты фарадеевского

импеданса

где х — угол наклона оси эллипса к абсциссе (другие параметры понят-

ны из рисунка).

Катодный вольтметр позволяет контролировать потенциал элект-

рода, а вольтметр переменного напряжения используется при подборе

амплитуды переменного сигнала от генератора. Эта амплитуда долж-

на быть такова, чтобы поляризация рабочего электрода не превышала

5—10 мВ.

Другой широко распространенный способ измерения импеданса

основан на использовании мостов переменного тока (Р-568, Р-5021).

Рис. 4.33. Блок-схема установки для. изме-

рения импеданса:

Г—-генератор переменного напряжения- Я —

ячейка; В — катодный вольтметр; ВП — вольт-

метр переменного напряжения; УТ — усилитель

* тока; ОС — осциллограф

Ри<г. 4.34. Эллипс, возникаю-

щий в результате суперпози-

ции сдвинутых по фазе сигна-

лов одинаковой частоты, про-

порциональных переменному

току и напряжению

Принципиально установка для измерения составляющих импеданса

электрохимической реакции в равновесном состоянии практически не

отличается от установки для измерения дифференциальной емкости

двойного слоя (см. с, 168). Единственное различие — в данном случае

нет необходимости использовать поляризационную схему. С помощью

современных мостов измеряют 7?

изм

и С

изм

в области частот перемен-

ного тока от 20 Гц до 100 кГц.

Наконец, наиболее перспективным путем измерения импеданса

являются автоматические установки, которые широко распространены

Д л

бе

^?г^л?

апример п

иб

°Р

Рм «Солатрон» (Великобритания),

«РАК» (США), «Такюсель» (Франция), «Хакуто Дэнки» (Япония)

Имеются, правда пока в сочень ограниченном количестве, такого рода

приборы и в нашей стране. Принцип работы автоматических прибо-

ров состоит в использовании фазочувствительных детекторов, т. е.

устройств, которые автоматически измеряют составляющую тока, на-

ходящуюся в фазе с опорным сигналом (напряжением от генератора)

и смещенную относительно опорного сигнала на 90°. Получающиеся

величины, как легко показать, пропорциональны активной и ре-

активной составляющим адмиттанса, т. е. 1//? и Ссо соответственно

264

ПРАКТИЧЕСКАЯ ЧАСТЬ

1. ОПРЕДЕЛЕНИЕ КИНЕТИЧЕСКИХ ПАРАМЕТРОВ РЕАКЦИИ

[ Ре

(С1Ч)

}

~ + ** [Ре(СЫ)

]

™ НА ПЛАТИНОВОМ ЭЛЕКТРОДЕ

Для работы используют обычную трехэдектродную ячейку с всжь

могательным электродом в виде цилиндра. Рабочий электрод из пла-

тиновой проволоки диаметром 0,05—0,1 мм впаивают в стеклянный

держатель. Можно также использовать тефлоновый держатель, ко-

торый натягивается на стеклянную трубочку. В этом случае нерабо-

чую поверхность проволоки изолируют от раствора полистиролом для

предотвращения затекания раствора между тефлоном и металлической

поверхностью. Нерабочую поверхность два—три раза покрывают

раствором полистирола в дважды перегнанном толуоле, а затем сушат*

электрод около 10 ч на воздухе. Длина электрода 2—4 мм.

Перед опытом'электрод очищают попеременно анодной и катодной

поляризацией (2—3 раза) в 0,05МН

, причем каждая длительно-

стью 10 мин. Поляризующий ток равен примерно 5—10 мА/см

. После

каждой поляризации раствор кислоты заменяют свежей порцией.

Растворы представляют собой разные соотношения смесей

[Ре(СН)

] и К

[Ре(СМ)

] на фоне 0,5 М КС1 или боратного буфера

при рН, близких к нейтральным (чтобы избежать влияния реакции

Н ^ н+ + <г). Состав буфера с рН 7,0—8,5 подбирают сливани-

ем

аД

растворов 0,05МН

В0

и 0,075М Ыа

. Соли, предварительно

перекристаллизовывают, растворы готовят по обычным методикам

(см. § 1.2). Суммарная концентрация окисленных и восстановленных

ионов в исследуемом растворе обычно не превышает 0,02 М. Приготов-

ленный раствор помещают в ячейку и I—2 ч продувают очищенным

азотом или аргоном.

С помощью измерительной установки измеряют составляющие

импеданса. Область частот переменного напряжения 40—10 000 Гц

(всего используют 5—6 частот).

Все параметры записывают в таблицу по образцу:

Состав р-ра

^ИЗМ

изм

«п .

1,С

<О

Расчет выполняют по формулам (4.71)—(4.74). Заметим, что эти рас-

четы можно легко запрограммировать и выполнять на простых ЭВМ.

Дальнейшие вычисления, связанные с построением прямых —.

— 1/]/~<о и 1 /С

со — 1/Ксо, следует проводить методом наименьших

квадратов [формулы (4.75), (4.76)]. Из величины 1Г, представляющей

265 '

собой тангенс угла наклона указанных выше прямых, в предположе-

нии равенства О^ « 0

0х

можно оценить коэффициенты диффузии

разряжающихся ионов. Расчеты *

, .*(««*>

а проводят по формулам

(4.75) и (4.77). ^

Следует заметить, что необходимые при проведений расчетов зна-

чения /?

ра

и С

д е

можно измерить предварительно в отсутствие

редокс-системы. Другой способ определения Я

ра

и С

дс

состоит в

проведении измерений при высоких частотах. Действительно как

следует из эквивалентной схемы (см, рис. 4.31), с ростом частоты пе-

ременного тока вклад фарадеевского процесса (нижняя ветвь экви-

валентной схемы) в суммарный импеданс будет снижаться и при дости-

жении^ определенных ^ (обычно это 10—20 кГц) можно считать, что

изм ~~ Сд.с» а /?

изм

= /?

ра

В качестве практических заданий предлагается с помощью мосто-

вого метода измерить импеданс при нескольких частотах (в интервале

от 40 до 10000 Гц) и рассчитать кинетические параметры редокс-реак-

ции на платиновом электроде в следующих растворах-

I Кд[Ре(СЫ)

] +3 • 10-

М Кз1Ре(СЛ

)

]; 0,01 М К

[Ре(СШ +

+ 0,001 М К

[Ре(СЫ)

]; 0,01 М К

[Ре(СМ)

+ 0 003М К(фо-

новый раствор — боратный буфер);

б) 0,01 М Кз(Ре(С1Ч)

] +3 . 10~*М К

[Ре(СШ; 0,01 М КЛРе(СШ +

+ 0,001 М К

ГРе(СМ)

]; 0,01МК

[Ре(СМ)

] + 0,003 М К

[РеЖ (фо-

новый раствор — боратный буфер).

В принципе аналогичные работы могут быть поставлены для изу-

г^

^™

ЧескИХ па

амет

Р°в реакции оксалатных ионов железа

1Ье(С

)

] + <г [Ре(С

)з!

~ (фоновый раствор - 0,5 М К

)

на Р1- и капающем Н^-электродах.

% ОПРЕДЕЛЕНИЕ КИНЕТИЧЕСКИХ ПАРАМЕТРОВ РЕАКЦИИ

[Ре(С^

]з-4.

-^[р

(С1\[)

]<- НА ПАССИВНОМ ЖЕЛЕЗНОМ ЭЛЕКТРОДЕ

Для измерений импеданса используется та же ячейка, что и в пре-

дыдущей работе. Рабочий электрод представляет собой отожженную

в водороде или под вакуумом железную проволоку диаметром 0,1—

0,3 мм. Электрод закрепляют в ячейке с помощью тефлонового держа-

теля. Нерабочую часть электрода изолируют от раствора полистиро-

лом. Длина электрода 3—5 мм.

Перед опытом электрод помещают на короткое время в 0,05 М раст-

вор Н

для удаления с поверхности воздушно-оксидной пленки,

промывают бидистиллятом и вносят в ячейку с фоновым раствором

боратного буфера 0,05 М (Н

В0

+ Ма

) при рН 7,0—8,5. Раст-

вор тщательно продувают в течение 1—2 ч очищенным азотом или ар-

гоном для удаления растворенного кислорода.

В фоновом растворе проводят предварительное катодное восстанов-

ление поверхности электрода катодным током 30—50 мА/см

в те-

чение 30 мин, затем пассивируют при потенциале 0,2 В (относительно

н.к.э.). Далее раствор в ячейке заменяют на исследуемый (содержа-

18&

щий смесь окисленных и восстановленных ионов в суммарной концент-

рации до 0,5 М).

Поскольку в данной системе токи обмена электрохимической реак-

ции намного ниже, чем на Р1, влияние диффузионного импеданса на

измеряемые величины практически отсутствует. Эквивалентная схема

в этом случае упрощается до схемы рис. 4.35. Для получения элемен-

тов данной эквивалентной схемы измерения импеданса необходимо

проводить при частотах переменного тока 10~

—10

Гц (из-за большой

величины

), т. е. для выполнения работы следует воспользоваться

простейшей установкой, описанной в начале раздела, либо соответ-

ствующей автоматической.

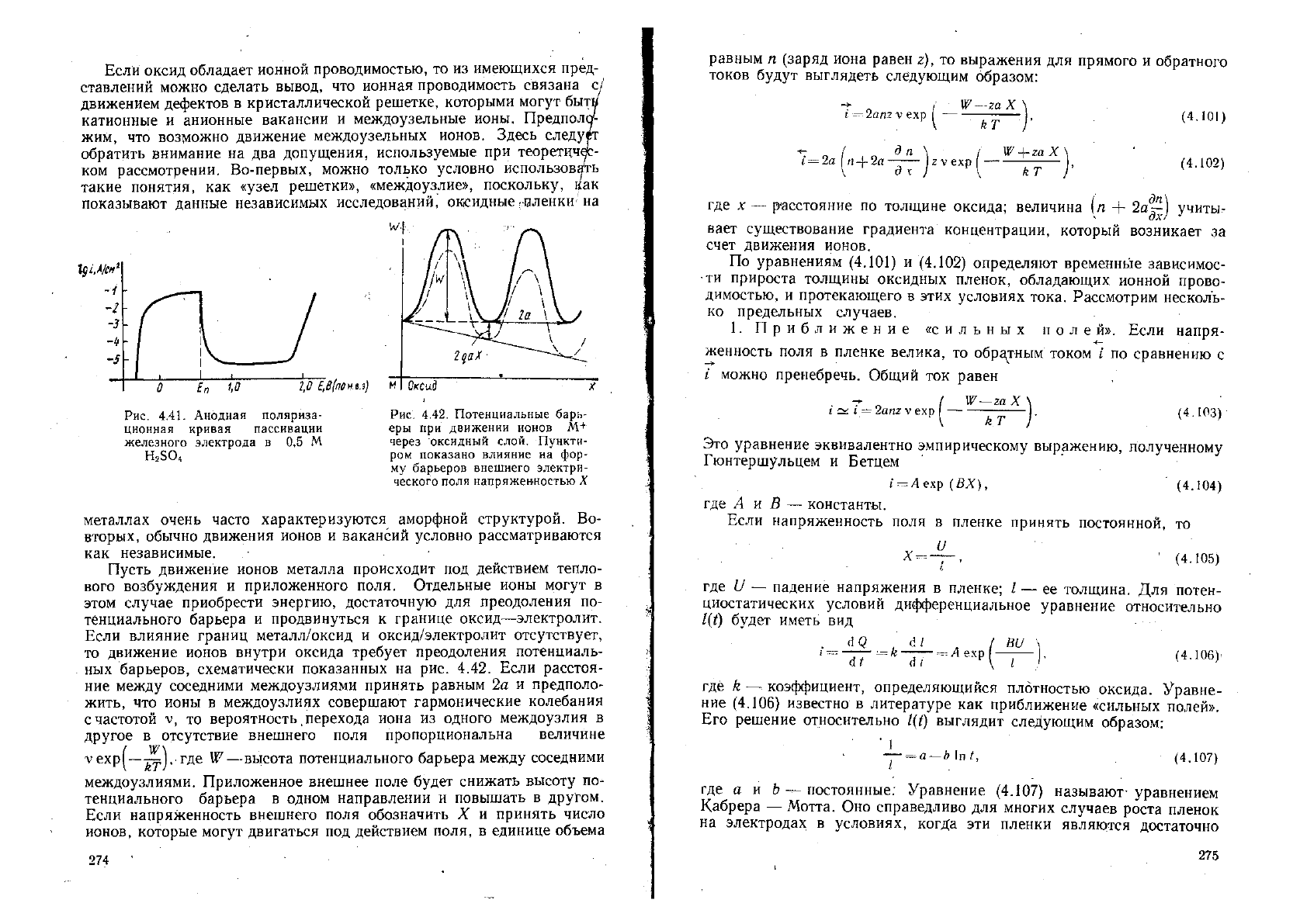
Рис. 4.35. Эквивалентная схема, мо-

делирующая окислительно-восста -

новительный процесс при большом

сопротивлении стадии разряда —

ионизации

Рис. 4.36. Диаграмма

Коул — Коул, соответст-

вующая схеме рис. 4.35

Анализ результатов измерений состоит в построений диаграмм

Коул

_Коул, которые представляют собой зависимость в комплекс-

ной плоскости реактивной составляющей импеданса (1/С

изм

(о) от ак-

тивной /?

изм

. Данная диаграмма для эквивалентной схемы (рис. 4,35)

имеет вид полуокружности, центр которой лежит на оси абсцисс и

смещен относительно начала координат на величину Лр-

ра

+ а

радиус равен #

. Схематически это показано на рис. 4.36.

/Для более точного расчета /?

из экспериментальных данных целе-

сообразно составить простую программу для ЭВМ. Расчеты кинети-

ческих параметров окислительно-восстановительного процесса про-

водятся как и в предыдущем задании.

Задание 1. Проанализировать влияние суммарной концентра-

ции редокс-системы на ток обмена. Для этого необходимо выполнить

измерения в трех растворах смесей (1 : 1)К

[Ре(СЫ)

] и К

Ре(С^Ы

при суммарных концентрациях (М): 10~

, 3 • Ю-

и. Ю-

(фоновый

раствор — боратный буфер).

Задание 2. Определить кинетические параметры данного окис-

лительно-восстановительного процесса на основании импедансных из-

мерений в следующих растворах: * _

а) 0,1 М №(СЫ)

1 + 0,003 М К

[Ре СНУ; 0 1 М

+ 0,01 М К

[Ре(СЫ)

]; 0,1 М К

(Ре(СМ)

] + 0,03 М К

1Ре(СМ)

] (фо-

новый раствор — боратный буфер);

183

б) 0,1 М Кз[Ре(СЫ)

] + 0,003 М К

[Ре(СМ)

]; 0,1 М

1Ре(СМ)

]

+ 0,01 М К

[Ре(СН)

]; 0,1 М К

(Ре(СН)

] + 0,03 М К

[Ре(СЫ)

] (фо-

новый раствор—боратный буфер).

§ 4.6. СОПРЯЖЕННЫЕ ЭЛЕКТРОХИМИЧЕСКИЕ РЕАКЦИИ,

КОРРОЗИЯ И ПАССИВАЦИЯ МЕТАЛЛОВ

Коррозия металлов в кислых растворах как пример сопряженных

реакций. В § 4.1 были рассмотрены основные кинетические закономер-

ности электрохимических процессов, относящихся к системам, в ко-

торых на поверхности металла протекает только одна электрохими-

ческая реакция. Во многих случаях на электроде параллельно идут

несколько электрохимических процессов. Например, катодное элект-

роосаждение металлов осложняется параллельной катодной реакцией

выделения водорода; параллельно анодной реакции выделения хлора

(хлорный электролиз) из водных растворов зачастую идет анодный

процесс образования молекулярного кислорода из воды.

Частным случаем параллельных реакций являются так называе-

мые сопряженные реакции, под которыми подразумеваются парал-

лельно протекающие на электроде протйвоположно направленные

(ащодные и катодные) процессы в условиях, когда внешний ток равен

нулю. Примерами таких реакций являются коррозия металлов (в кис-

лой среде параллельно идут анодное растворение металла и катодное

восстановление ионов водорода), бестоковое осаждение металлов (ка-

тодный разряд ионов металла с одновременным окислением входящего

в состав раствора органического вещества) и т. д.

Теоретический анализ параллельных процессов базируется на пред-

ставлении о независимом протекании отдельных реакций. Рассмот-

рим более подробно сопряженные реакции на примере растворения

металла М (например, Ре, 2п и т. п.) в подкисленном растворе собст-

венной соли (НА + МА, где А — анион). Суммарная реакция в та^ой

системе описывается уравнением;

М+пНА = МА

+ -|-Н

(4.80)

которое в действительности, как правило, включает две сопряженные

электрохимические реакции — отрыв*электронов от атомов М с об-

разованием ионов М

п+

и переход электронов через металлическую

поверхность к ионам Н

с образованием водорода:

М М

п+

~\~пе- (окисление) (4.81)

0++е~ —• Н

0 + 1/

(восстановление) (4,82)

Независимое протекание двух сопряженных реакций предполагает,

что каждая из них характеризуется своей поляризационной кривой

(рис. 4.37). Очевидно, что если бы в системе была возможна только ре-

173'

акция (4.81), то потенциал электрода определялся бы уравнением

Н^рнста

и (

иу

Ж. -

(4 83)

Р V Р' пР

п как

следует из рис. 4.37, скорость катодного процесса выделе,

?ия\одорода п7и 4 велика, что приводит к сдвигу потенциала в

ГОДНУЮ сторону и к ускорению анодного процесса ионизации метал-

ЙКК при некотором

нут равными и система придет в

так называемое стационарное со-

стояние (Е

— стационарный по-

тенциал или потенциал коррозии).

Рис 4 37, Поляризационные кри-

вые двух параллельных реакции

разряда — ионизации водорода

(Л и металла (2) при соизмери-

мых токах обмена (пунктиром по-

казаны парциальные поляризаци-

онные кривые соответствующих

реакций)

Рис 4.38. Поляризационные кри-

вые двух параллельных реакции

разряда — ионизации водорода

(Л и металла (2) в полулога-

рифмических координатах

ционарном потенциале называют стациим^п

определенную

потенциалов. Эти потенциалы

ха

ак

;

изу

ществу

ет принци-

анодных и катодных продессов

тен

циале

имеет

пиальное отличие этих величин. 1*н к

системы

результате чего

место баланс:по^^^^^^але^ балан-

г —л=г

183

разряда, характеризуются экспоненциальной зависимостью тока <*т

потенциала, а потому для изображения поляризационных кривйх

часто используются полулогарифмические координаты Е — В /Та-

ких координатах кривые, изображенное на рис. 4.37, буд^т иметь э4*д

представленный на рис. 4.38. На основании схематических зависи-

мостей (см. рис. 4.37 и 4.38) можно сделать несколько качественных

заключений. Во-первых, при стационарном потенциале электрода то-

ки анодных и катодных процессов связаны следующим соотношением:

(4.84)

Рис. 4.39. Схематическое изобра-

жение поляризационной кривой в

полулогарифмических координа-

тах (случай двух сопряженных

реакций)

которое в общем виде (при наличии п независимых электрохимических

процессов на одном электроде) будет выглядеть так:

п п

2 0

2 Ч< (4.85)

/=1 /=1

Во-вторых, если включить данную

систему во внешнюю электрическую

цепь

ои

пропускать через нее ток, зна-

чительно меньший /

, то потенциал

электрода практически не будет от-

клоняться от Е

. Если же внешний

ток (анодный или катодный) будет

значительно превышать /

, то потен-

циал электрода будет отклоняться от

и приближаться с ростом тока к

соответствующим зависимостям / — Е

или I — Е. Таким образом, измеряе-

мая поляризационная кривая в системе, характеризующейся нали-

чием двух сопряженных реакций, должна иметь вид, показанный на

рис. 4.39 (пунктиром изображены поляризационные кривые отдель-

ных реакций).

Очевидно, что выражение для внешнего тока (анодного /

,== — *

или катодного = /

), протекающего через систему, может быть

представлено в виде

ч—

— Н —

(4.86)

= к— (4.87)

или при' наличии п сопряженных реакций

= (4.88)

= (4.89)

Получим количественные выражения для зависимости тока от

потенциала при протекании на электроде двух сопряженных реакций

с соизмеримыми токами обмена. Для стационарных условий справедли-

173'

в& уравнение (4.84). Если принять во внимание, что 1

и /

малы, то

можно записать приближенное равенство

~Т

г у

(4.90)

Воспользовавшись уравнениями (4.12) и (4.13) для токов катодного

и анодного процессов, получим

/?т

^СОП51 + : , , 1П [Н-Ь]- (4 92)

Константы к

и к

можно получить из уравнений (4.12) и (4.13). Отме-

тим, что в эти выражения будут входить равновесные потенциалы со-

ответствующих реакций разряда—ионизации водорода и металла.

Вводя упрощения в уравнение (4.86), получаем

—•<—

+ 12 —

Н ~~

Н —

ехр

рехр (4.^3)

где АЕ = Е — Е

— отклонение потенциала от стационарного зна-

чения. Аналогичным образом, воспользовавшись уравнением (4.87),

можно получить выражение для зависимости катодного тока от по-

тенциала.

С учетом (4,91) уравнение (4.93) можно переписать в виде

( [(\—а

) пР АЕ~\ Г ад Р А Е 1)

*р [ ]~«*Р [ —Ц (4.94)

При малых АЕ экспоненты выражения (4.94) можно разложить в ряд.

Если ограничиться двумя первыми членами, то получим

. ят

Для катодного тока аналогичное выражение имеет вид

, _ , О-*»)"!^ д Е (4.96)

ЦТ

Из уравнений (4.95) и (4.96) следует, что при /

<С /

или <€ *с сдвиг

потенциала АЕ от стационарного значения мал. Этот вывод совпадает

с рассуждениями, приведенными выше. Заметим, также, что для со-

пряженных процессов *

выполняет ту же роль, что и ток обмена при

наличии в системе только одного процесса.

При больших отклонениях от стационарного потенциала, напри-

мер, в анодную сторону из уравнения (4.93) следует, что вторым чле-

271

ном в правой части можно пренебречь. Таким образом, /

в этих ур-

ловиях будет стремиться к /

. /

Анализируя экспериментальные поляризационные кривые (см.

рис. 4.39), можно получить информацию о Е

и /

, характеризующих

коррозионные свойства металла, а по углу наклона анодных и катод-

ных ветвей поляризационных кривых можно сделать заключения о

механизмах отдельных реакций суммарного процесса. Снятие поляри-

зационных кривых широко используют для изучения влияния состава

раствора и добавок огранических веществ (например, ингибитЬров)

на кинетику и механизм коррозионных процессов».

Следует отметить, что суммарная экспериментальная поляриза-

ционная кривая может быть разложена на парциальные кривые

(см. рис. 4.39) лишь при использовании дополнительных неэлектро-

химических методов. Например, скорость растворения металла, осо-

бенно в области потенциалов, где она очень мала, может определять-

ся радиоизотопным или другим аналитическим методом. Скорость

выделения водорода можно определить газометрически. Как видно из

рис. 4.38 и 4.39, при смещении потенциала в катодную сторону от

скорость выделения водорода увеличивается, а растворения метал-

ла уменьшается. Это явление называют протект-эффектом и широко

используют для защиты металлоконструкций от коррозии (катодная

защита).

Рассмотренные сопряженные реакции (4.81) и (4.82) характеризуют

так называемую кислотную коррозию. Очевидно, что сопряженными

растворению металла могут быть и другие катодные реакции, например

восстановление растворенного в коррозионной среде кислорода по од-

ной из следующих реакций:

+ 4Н+ + 4е~ = 2Н

0 (4.97)

ИЛИ

+2Н

0 + 4е- = 40Н~ (4.98)

а также восстановление молекул воды

0+е- = 1/

+ 0Н- (4.99)

И Т. Д.

Реакции (4.97) и (4.98) характеризуют кислородную коррозию, а

(4.99) — щелочную коррозию, поскольку наиболее часто сопряженным

процессом эта реакция является в щелочных растворах. На рис. 4.40

представлены поляризационные кривые, когда катодным сопряжен-

ным процессом являются реакции выделения водорода из воды и вос-

становления растворенного кислорода. При этом выделение водорода

из воды происходит по механизму замедленного разряда, а восстанов-

ление кислорода имеет сложный механизм: со сдвигом потенциала в

катодную сторону последовательно реализуются механизм замедленно-

го разряда, а затем смешанный и диффузионный механизмы. Как видно

из этого рисунка, в зависимости от природы металла вид поляризаци-

онных кривых меняется; разными условиями будет характеризоваться

273 7 Зак. 434 193

и стационарное состояние системы. Принципиально получение ана-

литических выражений для поляризационных кривых в любом из

возможных случаев не составляет большого труда. Более сложным и

практически важным является то, что в ходе анодного растворения ме-

талла его поверхность подвергается значительным изменениям, кото-

рые, в свою очередь, оказывают влияние на кинетику протекающих

процессов.

Пассивация металлов. Для большинства металлов при их анодной

поляризации в некоторых областях потенциалов наблюдается резкое

снижение тока растворения.

Как видно из рис. 4.41, при

достижении потенциала Е

наблюдается разкий спад

тока (иногда на 5 — 8 поряд-

ков). При дальнейшей анод-

ной поляризации ток мало

завйсит от потенциала в

довольно широкой области,

а затем вновь увеличивается.

Явление резкого снижения

тока растворения металла но-

сит название пассивации.

Для объяснения природы

пассивности были предложе-

ны пленочная и адсорбцион-

ная теории пассивации. Со-

гласно первой, замедление

скорости растворения метал-

ла обусловлено формирова-

нием на металле в ходе анод-

ного растворения фазовой

пленки оксида (или гидро-

ксида) по схеме

+ лН

0 = МО

+ 2п Н+ + 2пе-

(4.100)

Адсорбционная теория объясняет пассивацию образованием на

поверхности металла при анодной поляризации моно- или даже суб-

монослоя адсорбированного кислорода. Под действием адсорбирован-

ного кислорода меняется энергетическое состояние поверхностных

атомов металла,, происходит блокировка активных центров, что и

приводит к замедлению коррозионного процесса. Имеющиеся в лите-

ратуре данные указывают на необходимость учета для истолкования

природы пассивации как первого, так и второго механизмов.

Подробно разработаны теоретические вопросы, связанные с кине-

тикой роста оксидных пленок при пассивации металла. Рассмотрим

основные из них.

Рис. 4.40. Поляризационные кривые для

трех металлов в нейтральных растворах:

стационарный потенциал для металла Ми опре-

деляется равенством скорости растворения ме-

талла и предельным диффузионным током вос-

становления кислорода; для металла М

— равен-

ством скоростей растворения металла и восста-

новления кислорода в области смешанной кине-

тики; для металла М

— равенством скоростей

растворения металла и катодного восстановления

водорода из молекул воды; 1, 2, 3

—

парциальные

кривые окисления соответствующих металлов

193

Если оксид обладает ионной проводимостью, то из имеющихся пред-

ставлений можно сделать вывод, что ионная проводимость связана с/

движением дефектов в кристаллической решетке, которыми могут быть

катионные и анионные вакансии и междоузельные ионы. Предполо-

жим, что возможно движение междоузельных ионов. Здесь следу!

обратить внимание на два допущения, используемые при теоретичес-

ком рассмотрении. Во-первых, можно только условно использовать

такие понятия, как «узел решетки», «междоузлие», поскольку, ^ак

показывают данные независимых исследований," оксидные пленки на

Рис. 4.41. Анодная поляриза-

ционная кривая пассивации

железного электрода в 0,5 М

Рис. 4.42. Потенциальные барь-

еры при движении ионов М+

через оксидный слой. Пункти-

ром показано влияние на фор-

му барьеров внешнего электри-

ческого поля напряженностью X

металлах очень часто характеризуются аморфной структурой. Во-

вторых, обычно движения ионов и вакансий условно рассматриваются

как независимые.

Пусть движение ионов металла происходит под действием тепло-

вого возбуждения и приложенного поля. Отдельные ионы могут в

этом случае приобрести энергию, достаточную для преодоления по-

тенциального барьера и продвинуться к границе оксид—электролит,

Если влияние границ металл/оксид и оксид/электролит отсутствует,

то движение ионов внутри оксида требует преодоления потенциаль-

ных барьеров, схематически показанных на рис. 4,42. Если расстоя-

ние между соседними междоузлиями принять равным 2а и предполо-

жить, что ионы в междоузлиях совершают гармонические колебания

с частотой V, то вероятность

перехода иона из одного междоузлия в

другое в отсутствие внешнего поля пропорциональна величине

Vеxр(—где №—высота потенциального барьера между соседними

междоузлиями. Приложенное внешнее поле будет снижать высоту по-

тенциального барьера в одном направлении и повышать в другом.

Если напряженность внешнего поля обозначить X и принять число

ионов, которые могут двигаться под действием поля, в единице объема

274 7 Зак. 434 193

равным п (заряд иона равен г), то выражения для прямого и обратного

токов будут выглядеть следующим образом:

- _ / V—га X \

1=2апгуехр ( —•), (4.101)

^ О I ,

дп

\ I

№

+ гаХ\

+2а

ТГг

Уехр

(~ кт Г

(4Л02)

где х — расстояние по толщине оксида; величина (п + 2а^] учитьь

вает существование градиента концентрации, который возникает за

счет движения ионов.

По уравнениям (4.101) и (4.102) определяют временные зависимос-

ти прироста толщины оксидных пленок, обладающих ионной прово-

димостью, и протекающего в этих условиях тока. Рассмотрим несколь-

ко предельных случаев.

1. Приближение «сильных полей». Если напря-

женность поля в пленке велика, то обратным током I по сравнению с

I можно пренебречь. Общий ток равен ,

[

УР—га

X \

г 2апг V

ехр

-— —

I кТ )

(4.103)

Это уравнение эквивалентно эмпирическому выражению, полученному

Гюнтершульцем и Бетцем

ехр (ВХ), (4.104)

где А и В — константы.

Если напряженность поля в пленке принять постоянной, то

Х = —

• (4.105)

где V — падение напряжения в пленке; I — ее толщина. Для потен-

циостатических условий дифференциальное уравнение относительно

/(/) будет иметь вид

. (1<э •

6 1

[ ви \

^ТГ^ЧГ"). • (4.106).

где к — коэффициент, определяющийся плотностью оксида. Уравне-

ние (4.106) известно в литературе как приближение «сильных полей».

Его решение относительно

1(1)

выглядит следующим образом:

' 1

— = а —И п/, (4.107)

где а и Ь-г- постоянные: Уравнение (4.107) называют-уравнением

Кабрера — Мотта. Оно справедливо для многих случаев роста пленок

на электродах в условиях, когда эти пленки являются достаточно

193

тонкими (X — велико) или барьер, который преодолевают движущи-

еся ионы, в основном локализуется на границе металл—оксид.

2. П р и б л и ж е н и е «слабых п о л е й». В условиях, ког-/

да обратным током пренебречь нельзя, из уравнений (4.101) и (4.102^

следует

- ч- /и?

I — I — I

Щп V ехр I —

дп ( УР + гаХ \

(А шя

— 4

з —

ех

р —— . (4.108)

д х \ к Г }

ч , ( хаХ\ гаХ

ЕСЛИ гаХ

<С

ЬТ (приближение «слабых полей»), то ЗШ ^г) «

\Г/ + гаХ « № и уравнение (4Л08) упрощается до

' ?

' (4,109)

•

д х

где к

к%

— постоянные.

Первый член в правой части уравнения (4.109) отражает рост ок-

сида на электроде под действием градиента потенциала (миграцион-

ный механизм)

а второй — градиента концентрации (диффузионный

механизм).

Если реализуется миграционный механизм, т. е. вторым членом

в правой части (4.109) можно пренебречь, то для потенциостатических

условий выражение для зависимости толщины пленки и тока от вре-

мени будут выглядеть так:

у" . (4Л

Ю)

. (4.111)

Аналогичного вида функциональные зависимости I и I от времени,

правда, с другими коэффициентами,получаются и при диффузионном

механизме роста оксида. Точное решение задачи в этом случае назы-

вают законом Крофта. Отметим, что оба механизма роста оксидных

пленок, вытекающие из уравнения (4.109), характерны для металлов,

на которых формируются весьма толстые слои оксида.

3. Туннельный механизм роста оксидных

плен о к. Кроме перемещения собственно ионов при росте оксида

замедленной стадией процесса может быть туннелирование электронов

через оксид. Это явление наблюдается для оксидных пленок, по тол-

щине не превышающих ~4 нм. Механизм нарастания оксида сле-

дующий: происходит замедленное туннелирование электрона через

оксид от границы оксид—раствор к металлу, а затем быстрое переме-

щение ионов кислорода или металла через пленку с образованием но-

276

вых молекул оксида. Эти представления, развитые Хауффе и Ильш-

яером, приводят к следующему уравнению:

• (_'*'№),

.„

где А — константа; т

— масса электрона; № —высота энергети-

ческого барьера, под которым туннелируют электроны; к — постоян-

ная Планка. Из (4.112) следует так называемый прямой

логарифми-

ческий закон роста оксида

М^А^В^п!. (4.113)

В настоящее время активно развиваются теоретические представления,

связанные <с механизмами роста и разрушения оксидных пленок на

металлах. При этом используется широкий круг методов, включая не

электрохимические.

ПРАКТИЧЕСКАЯ ЧАСТЬ

1. ИССЛЕДОВАНИЕ КОРРОЗИИ ЖЕЛЕЗА (СТАЛЕЙ) В КИСЛЫХ

РАСТВОРАХ

Для проведения измерений может быть использована трехэлект-

родная ячейка, в которой пространства для рабочего и вспомогатель-

ного электродов разделены краном или впаянным стеклянным фильт-

ром (см. например, рис. 1.4). В качестве вспомогательного электрода

обычно используют платиновую проволоку. Поскольку скорость элект-

рохимического процесса в области активного растворения металла

может быть весьма велика, для уменьшения омического падения по-

тенциала (особенно это важно для растворов с малой проводимостью)

желательно использовать электрод сравнения, снабженный капилля-

ром Луггина. Собственно электродом сравнения может быть кало-

мельный, хлорсеребряный, водородный в том же растворе или любой

другой.

Перед экспериментом необходимо вынуть из ячейки электроды, '

ячейку тщательно промыть и укрепить на столе с цомощью штатива

и вставить все детали и электроды.

В качестве исследуемого электрода может б*>пъ использована фоль-

га, пластина или проволока. Фольгу или пластину желательно выре-

зать в форме флажка, примерные размеры которого (в мм) показаны

на рис. 4.43. Верхняя часть электрода делается узкой; для того, чтобы

снизить погрешность в определении площади рабочего электрода.

Площадь рабочего электрода подбираеуся исходя из возможностей по-

тенциостата (максимального тока потенциостата) и максимальных то-

ков в области активного растворения металла. Так, на железе в об-

ласти активного растворения в 0,5 М Н

токи достигают

~100мА/см

, Максимальный выгодной ток потенциостата П-5827М

7 Зак. 434 193

составляет 250—300 мА. Учитывая, что истинная поверхность элект-

рода обычно в несколько раз превышает видимую, площадь электрода

следует ограничить 0,5—1 см

. Заметим, что при расчете площади по-

верхности электрода следует учитывать обе стороны пластинки.

Исследуемый электрод припаивают или приваривают точечной свар-

кой к токоотводу (медная или никелевая проволока) и закрепляют с

помощью держателя, который изготавливают из тефлона. Нерабо-

чую часть поверхности изолируют от раствора полистиролом (исполь-

зуют раствор полистирола в химически чистом толуоле) или другим

полимером. Часто для этих целей применяют

эпоксидный клей. При выборе изолирующего по-

лимера необходимо проявлять определенную

осторожность и предварительно убедиться в

том, что он не растворяется в исследуемом рас-

творе. Последнее, естественно, может сильно ис-

казить истинное поведение металла в изучаемой

системе.

Весьма точно поверхность рабочего электрода

(видимую) определяют с помощью компаратора;

более грубо она может быть определена с помощью

линейки.

Перед опытами электрод аккуратно зачищают

тонкой наждачной бумагой или тонким стеклян-

ным порошком для удаления с поверхности при-

месей. Затем обезжиривают поверхность этиловым

спиртом и многократно промывают электрод бидистйллятом. Очист-

ку реактивов проводят так, как описано в § 1.2.

Собранную ячейку заполняют раствором серной кислоты или под-

кисленного раствора соли и в течение 30 мин продувают инертным

газом (аргоном) или азотом для удаления кислорода из раствора и

пространства над раствором. Используемый для этих целей газ под-

вергается дополнительной очистке и осушке (подробности см. в § 1.2).

Выводы электродов присоединяют к соответствующим клеммам

потенциостата, который включают в сеть и приводят в рабочее сос-

тояние. Обычно значение стационарного потенциала реализуется

примерно через 5—10 мин после помещения электрода в раствор. Это

значение фиксируется с помощью катодного вольтметра.

Для .снятия зависимости анодного тока от потенциала в режиме

автоматической развертки потенциала на потенциостате устанавли-

вают соответствующую скорость развертки потенциала (обычно это

5—20 мВ/мин). ^Включают соединенный с потенциостатом потенцио-

метр (например, двухкоординатный Н-306). Подбирают необходимые

диапазоны тока (ось V) и потенциала (ось X) таким образом, чтобы

уместить всю кривую на листе самописца. Начальное положение пера

самописца фиксируют ручками установки нуля.

На блоке задатчика потенциала потенциостата (П-5827М) или

программатора (ПР-8), соединенного с потенциостатом ПИ-50-1, уста-

Рис. 4.43. Форма

электрода для изу-

чения коррозии

287

навливают значение стационарного потенциала и потенциостат при-

водится в режим включенной ячейки. В условиях, когда на электрод

накладывается потенциал, соответствующий стационарному состоя-

нию, ток через ячейку должен отсутствовать. Это можно проверить

амперметром, подключенным к потенциостату, а также по отсутствию

отклонения пера самописца в направлении координаты V.

После проведения указанных подготовительных работ включают

развертку потенциала и самописец начинает записывать анодную /,

^-кривую. Примерный вид поляризационной кривой на Ре-электроде

в 0,5 М Н

ЗР

показан на рис. 4.41. По окончании измерений поляри-

зация отключается и в течение примерно 10 мин можно наблюдать

смещение потенциала в катодную сторону до достижения стационар-

ного значения. Полученное значение стационарного потенциала может

на 5—10 мВ отличаться от начального, что обычно является следствием

появления в растворе после прохождения электрода через область

активного растворения некоторого количества ионов железа. Поэтому

перед проведением последующих измерений необходимо сменить раст-

вор.

Для определения стационарной скорости растворения металла (или

коррозионного тока) снимают катодную и анодную поляризационные

кривые вблизи стационарного потенциала в режиме ручного управле-

ния потенциостатом. Для этого на электрод с помощью потенциостата

накладывают потенциал примерно на 250 мВ более катодный, чем

стационарный, и фиксируют протекающий катодный ток. Далее по-

тенциал электрода последовательно через 40—50 мВ смещают в анод-

ную сторону и регистрируют соответствующие значения тока. При

переходе через стационарный потенциал ток меняет полярность. Из-

мерения заканчивают после того, как накладываемый на электрод

потенциал достигнет величины на 200—250 мВ более анодной, чем

Ее,

Результаты измерений записывают в таблицу:

Е, мВ

мА

1, мА/ СМ

П '

По окончании измерений выключают потенциостат и отсоединяют

ячейку.

На основании данных поляризационных измерений вблизи ста-

ционарного потенциала на миллиметровке строят график зависимости

логарифма плотности тока от потенциала. С помощью линейной экст-

раполяции полученных кривых определяют коррозионный ток и угол

наклона поляризационных кривых выделения водорода и растворения

металла.

279