Czichos H., Saito T., Smith L.E. (Eds.) Handbook of Metrology and Testing

Подождите немного. Документ загружается.

898 Part D Materials Performance Testing

Magnetic lines

of force

Solenoid Longitudinal crack

will not be visible

Crack at 45° may

be visible

Transverse

crack will

be visible

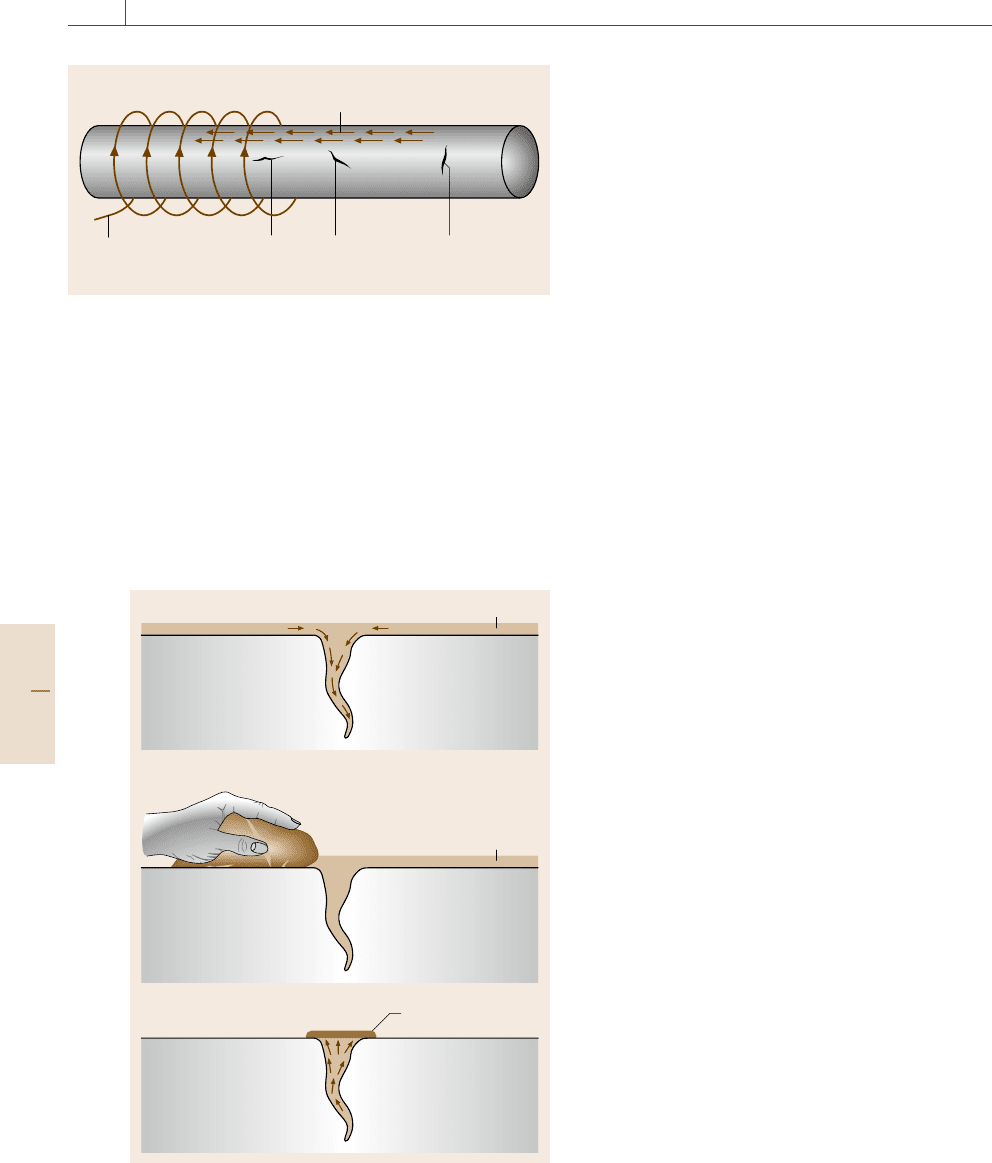
Fig. 16.22 Crack orientation in relation to the magnetic ﬁeld

principle of the magnetic particle inspection method.

The defect will cause some of the lines of magnetic

force to depart from the surface and thus to create

a magnetic leakage ﬁeld. Fine iron (powder) particles,

applied to the surface of the specimen, are attracted

to the area of ﬂux leakage, creating a visible indica-

tion of the ﬂaw. The magnetic leakage ﬁeld will hold

the particles in a ridge on top of the crack (Fig. 16.21).

By taking advantage of this effect an accumulation of

magnetic particle forms, which is much wider than the

Solid

Liquid

Developer

Fig. 16.23a–c Principle of liquid penetrant inspection

crack itself, thus making an otherwise invisible crack

visible.

If, for example, a crack is oriented perpendicular to

the ﬂux lines the effect of disturbance of the magnetic

ﬁeld is at a maximum compared with other orientations.

However, in this situation the leakage ﬁeld is strongest

and provides the clearest indication of a defect. Fig-

ure 16.22 demonstrates the orientation of a crack in

relation to the direction of the magnetic ﬁeld. The cylin-

drical object was magnetized with a solenoid coil that

provides longitudinal magnetization of the workpiece,

suitable for the examination of transverse cracks. Lon-

gitudinal cracks are not visible using this magnetization

procedure. From the previous example it is clear that

a good magnetic particle inspection should always be

carried out with the magnetic ﬁeld in two different di-

rections, preferable in two orthogonal directions.

16.1.5 Liquid Penetrant Inspection

Liquid penetrant inspection is an old but effective NDT

method of examining surface areas for cracks, or dis-

continuities. In railway and casting fabrication this

technique is widely practiced to examine the surfaces

by the oil and whiting method. This involves dunk-

ing parts, such as locomotive parts or big bells (made

from bronze), in large tanks ﬁlled with heavy oil diluted

with kerosene. After removal and cleaning, the surface

of the specimen is than coated with a ﬁne suspension

of chalk in alcohol so that a white surface layer was

formed. The residual oil in the surface-opening cracks

seeps out and colors the white coating grey. At the time,

more-effective penetrating oils containing highly visible

dyes (usually red) were developed to enhance ﬂaw de-

tection capability. This method known as color-contrast

dye penetrant is still used quite extensively. Due to the

reason that this method is relatively simple (although

care must be taken because there are several require-

ments which have to be regarded during examination)

to handle. It should be clear that this method is re-

stricted to defects open to the surface. The principle

procedure of liquid penetrant inspection is illustrated

in Fig. 16.23. The penetrant is drawn down into the open

crack by capillary action (a). Excess surface penetrant

is then removed (b). Developer powder on the surface

draws out penetrant liquid, which seeps into and dis-

colors the powder. The crack becomes visible on the

surface. One of the advantages of liquid penetrant in-

spection is that all materials can be inspected if it is

guaranteed that the material is resistant to the liquid

used.

Part D 16.1

Performance Control 16.1 Nondestructive Evaluation 899

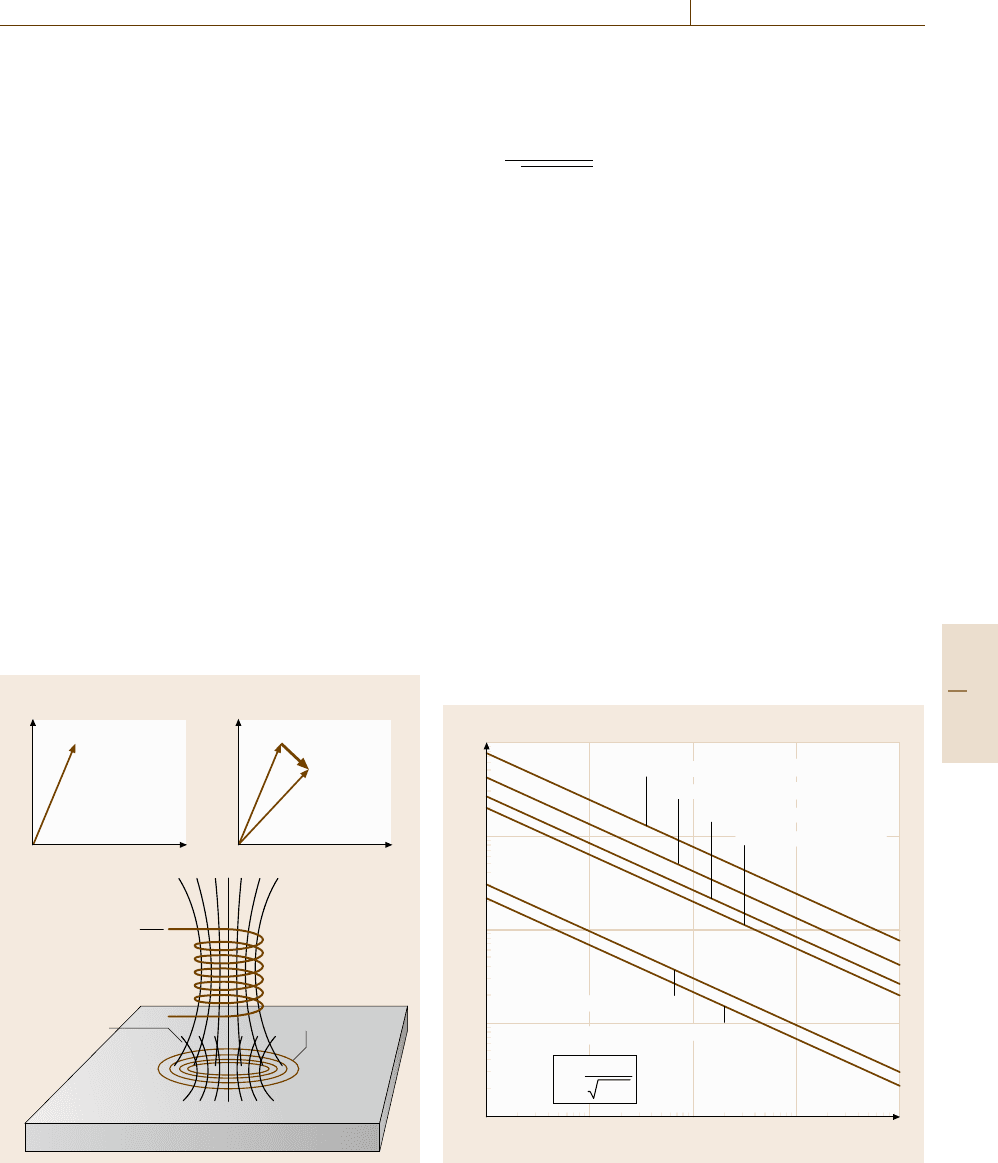
16.1.6 Eddy-Current Testing

A varying electric current ﬂowing in a coil (eddy-

current probe) generates a varying magnetic ﬁeld [16.17,

18]. In a specimen with electric conductivity in the

proximity of this coil, eddy currents ﬂowing in a closed

loop in the surface layer of the specimen are produced

(Fig. 16.24). Defects at materials surfaces in the oppo-

site of the eddy-current probe can be detected by the

change of the electric coil impedance, which will be,

e.g., displayed for evaluation by the test instrument con-

nected to eddy-current probe. Cracks and other surface

in homogeneities or discontinuities modify the eddy

currents generated in the specimen. The coil impedance

is changed in relation to a surface without defects. Prac-

tical application using eddy-current techniques is only

possible if sensitive electronic devices are available that

are able to measure the very small changes of the mag-

netic ﬁeld caused by a defect. An important phenomena

of eddy-current testing is the so called skin effect. There

is no homogenous current distribution within the spec-

imen; it is mainly concentrated at the contact surface

of the eddy-current probe. This physical phenomenon

is the reason why eddy-current testing is basically lim-

ited to thin test objects or only in a surface layer of

thicker objects. The penetration depth δ of eddy cur-

rent can be calculated using (16.6) and depends on the

Without defect

With defect

Alternating current

Secondary

magnetic field

Electrically conductive material

Eddy currents

Magnetic field

Fig. 16.24 Principle of eddy-current testing

frequency ν, the conductivity σ, the permeability of the

free space μ

and the relative magnetic permeability μ

For nonferromagnetic materials μ

is equal to 1

δ =

√

πνμ

. (16.6)

The frequency used in eddy-current testing ranges

from a few kHz to more than 5 MHz. At lower fre-

quencies the penetration depth δ is relatively high, as

derived from (16.6), but the sensitivity to the detec-

tion of discontinuities is poor, while the opposite is

true at higher frequencies. Values of δ versus the fre-

quency are plotted in Fig. 16.25. However, it should

be considered that these estimations have been made

under simpliﬁed assumptions. In practical applications

the penetration depth δ also depends on the character-

istic of the eddy-current probe. For crack detection in

and near the surface area, the penetration depth δ must

be optimized in relation to the sensitivity of detection.

For wall thickness measurement (detection of corrosion

phenomena) δ must be at least that of the component

thickness.

Figure 16.25 demonstrates that ferritic materials

have very high permeability values and therefore only

low penetration depth can be achieved (fractions of mil-

limeter). This is the reason why eddy-current techniques

cannot be applied to defect detection in certain depths or

wall thickness measurements. A magnetizing facility up

Penetration depth δ (mm)

Austenitic steel (μ

= 2, σ =2 m/(Ω mm

))

Iron (μ

= 200, σ =10m/(Ω mm

))

Iron (μ

= 2000, σ =2 m/(Ω mm

))

Brass (σ =12m/(Ω mm

))

Aluminum (σ =35m/(Ω mm

))

Copper (σ =56m/(Ω mm

))

100

0.1

0.01

Exciting frequency f (Hz)

δ =

fσμ

503

Fig. 16.25 Penetration depth versus eddy-current frequency

Part D 16.1

900 Part D Materials Performance Testing

Head checks

Fig. 16.26 Head checks at the gauge corner

to the saturation ﬁeld can be helpful due to the reduction

of the relative permeability.

On the other hand austenitic steel or nonferrous ma-

terials are suitable for the application of eddy-current

methods, and a broad application of this method is in

the aircraft industry.

The application of eddy-current techniques em-

braces a wide industrial ﬁeld from the aircraft industry,

the railway industry to the power-generation industry

etc. Out of these wide ﬁelds of use, an example from

the railway industry will be presented [16.19]. The in-

spection of railway wheels, known and referred to as

the inspection of the railway gauge corner using eddy

current, has increased in recent years. In Fig. 16.26

a special defect type is shown: so-called head checks.

Head checks are cracks in the gauge corner and can be

identiﬁed by their high number, having a separation of

2–7 mm. Head checks initially grow into the interior of

the rail at an inclination angle of 15 to 30

◦

. Rail gauge

corner inspection is necessary to avoid rail damage such

Fig. 16.27 Broken rail caused by head checks

as that illustrated in Fig.16.27 and is necessary to avoid

accidents and save human lives.

However, an increase in surface or near-surface

defects, such as head checks (Fig. 16.26) requires in-

spection techniques with a high detection and sizing

potential to facilitate the identiﬁcation of such defects.

Another condition has to be considered, which is the

speed of the inspection train. Inspection can be per-

formed at up to 100 km/h.

To summarize, the eddy-current techniques proved

to be most suitable for such application, because eddy-

current probes have a high resolution when the head

check distance is within the range of a few millimeters

and modern technology means measurements can take

place at higher speeds, which is an important economic

factor.

16.2 Industrial Radiology

Industrial radiology is typically applied for the volu-

metric inspection of industrial products and installa-

tions [16.20,21]. The basic set up consists of a radiation

source in front of the object to inspect and an area de-

tector behind the object. The classical detector is an

x-ray ﬁlm. New electronic area detectors are gradually

substituting ﬁlm. The radiation source can be an x-ray

generator, a gamma source or a particle radiator. Objects

of all possible materials and thicknesses can be in-

spected, provided the right radiation source and energy

is selected. There exist practical limitations to the upper

material thickness, e.g. 50 cm penetration length in steel

or 2 m in concrete (at a radiation energy of 12 MeV).

Radiology dates back to the discovery of x-rays by

W. C. Roentgen in 1895 and the discovery of gamma

radiation by H. Becquerel in 1896. After the devel-

opment of high-vacuum x-ray tubes with energies up

to 100 keV in 1913, radiological techniques have been

introduced into industrial practice. The description of

the ﬁrst computerized tomography (CT) system by

G. Hounsﬁeld and A. Cormack in 1973 was a further

milestone in the development of radiation techniques

Part D 16.2

Performance Control 16.2 Industrial Radiology 901

in medical and industrial applications. In acknowledge-

ment all four scientists received Nobel prices (for the

methods of computerized tomography see Sects. 16.3

and 16.5). Over the last decades tremendous progress

in hardware has occurred, such as the development

of radioscopic systems with x-ray image intensiﬁers,

microfocus x-ray tubes, digital detector systems. This

progress was accompanied by an enormous increase

in computing capabilities which made the introduction

of digital techniques possible, such as digital image

processing and enhancement, automated defect recog-

nition, data reconstruction, and three-dimensional CT

applications. Nowadays, the increased capabilities of

digital detection systems, such as phosphor imaging

plates (computed radiography) and ﬂat-panel detectors

(digital detector arrays), indicate a new era in radiol-

ogy.

16.2.1 Fundamentals of Radiology

Generation of Radiation

Radiation is used in industry, due to its capability to

penetrate opaque material to visualize the inner struc-

ture of components. The radiation photon has a dual

character, acting sometimes like a particle and at other

times like a wave. Consequently, the radiation photon is

characterized by its energy E or its wavelength λ or fre-

quency ν. Planck postulated that the energy of a photon

is proportional to its frequency

E = hν (16.7)

with Planck’s constant h. All photons have equal veloc-

ity,

c =νλ , (16.8)

no electric charge, and no magnetic moment. x-ray or

gamma radiation is fully characterized by its energy.

They are distinguishable only due to their origin but not

due to their properties.

X-rays are usually produced by the deceleration of

high-energy electron impinging by a metallic target.

Gamma rays are of nuclear origin. Whereas x-rays orig-

inate in the electron structure of the atom, gamma rays

are emitted by the de-excitation of atomic nuclei in a nu-

clear reaction. The emission of gamma rays is usually

associated with the emission of alpha and beta particles.

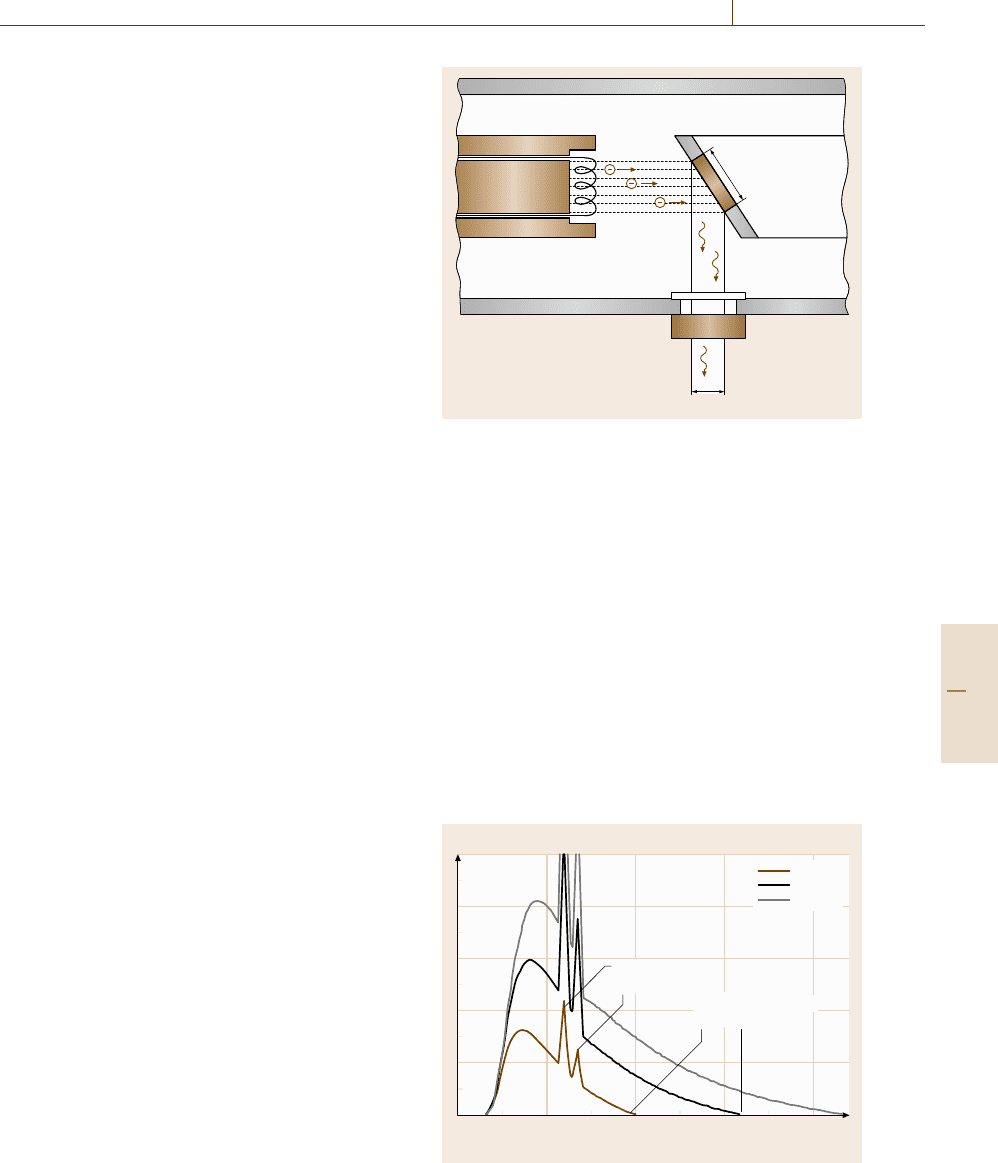
X-rays are generated in x-ray tubes, which consist

of a cathode and an anode made from heavy high melt-

ing metal (Fig. 16.28). Electrons are emitted from the

cathode and accelerated to the anode in a high-voltage

electrical ﬁeld. When the electrons with kinetic energy

Cathode

Vacuum window

Filter

Effective

focal size

X-rays

Actual

focal size

Target/Anode

Fig. 16.28 Principle of the x-ray tube

/2 hit the target of the x-ray tube the energy is

transformed in several ways yielding the production

of: (i) bremsstrahlung with a continuous spectrum, and

(ii) characteristic radiation (Fig. 16.29).

Bremsstrahlung is produced when the electron in-

teracts directly with the nucleus of the target atom. The

electron is stopped by the nucleus (near ﬁeld) and all

its kinetic energy is transformed into a quantum of ra-

diation. Because most of the impinging electrons also

interact with the electrons of the target atoms they lose

a part of their energy to remove an electron from an

atom. The remaining kinetic energy of the electron can

be transformed into an x-ray photon. In general, x-rays

photons of many energies are emitted forming the con-

tinuous bremsstrahlung spectrum. The voltage of the

Relative intensity

Characteristic

lines

Maximum energy

= Ue

0 50 100 150 200

E (keV)

100 kV

160 kV

220 kV

Fig. 16.29 Typical x-ray spectrum

Part D 16.2

902 Part D Materials Performance Testing

accelerating electrical ﬁeld gives the maximum energy

of the emitted x-ray photons.

When an electron is removed from the target atom

by the impinging electron, the atom is left in an excited

state. Recombination processes within the electron shell

yield the emission of one or more photons with energy

characteristic for the atom. As a result, the continuous

bremsstrahlung spectrum is overlaid by characteristic

spectral lines (compare Fig. 16.29).

The target of a x-ray tube can stop all impinging

electrons (thick or absorption target) as used in most

of the industrial x-ray tubes, or stop only a part of the

electrons (thin or transmission target) as used in micro-

focus tubes. Because most of the electron’s energy is

converted into heat (about 95%), overheating of the tar-

get has to be avoided. Therefore, the anode to which

the target is attached typically consists of a material

with high thermal conductivity, such as copper. Often

it is necessary to cool the anode by directly injecting

coolant. Another way of solving the problem of local-

ized overheating of the target is by using a rotating

anode.

Gamma rays are emitted during the spontaneous de-

cay of unstable isotopes. The decay is accompanied by

the emission of alpha or beta particles. Each emission

transforms the parent isotope into a daughter isotope

having a different mass and nuclear charge. This pro-

cess continues until the daughter isotope is stable. This

is described by the half-life T required for one half of

the original number of atoms to decay or change to the

daughter atoms. The number of atoms disintegrating per

unit time can be expressed by

N = N

−λt

(16.9)

with the total number of parent atoms N

, and the decay

constant λ. The half-life is given by

T = ln 2/λ = 0.693/λ . (16.10)

Artiﬁcially produced isotopes such as Ir-192 or Co-60

are widely used as sources of radiation for technical ra-

diography. The emitted gamma-ray spectrum consists of

separated lines with energies characteristic for the par-

ticular isotope. Both isotopes are obtained by neutron

bombardment of the naturally existing stable isotopes

Co-59 and Ir-191

Co +n →

Co +γ,

191

Ir +n →

192

Ir +γ. (16.11)

Figure 16.30 shows the disintegration scheme for Co-

60. As a result two gamma lines with 1.173 and

1.332 MeV are observed.

5.24 a

–

(99.85 %)

–

(0.15 %)

1.173 MeV

1.332 MeV

Fig. 16.30 Dis-

integration series

of Co-60

Interaction with Matter

Attenuation Law. Photons interact with a nucleus or an

orbital electron of the attenuating material. The interac-

tion of photons with matter can be classiﬁed into three

predominant types: (i) the photoelectric effect, (ii) scat-

tering, and (iii) pair production. Photodisintegration is

neglected due to its minor contribution. The attenuation

law is described assuming a narrow beam geometry and

monochromatic radiation (Fig. 16.31). Considering an

incremental attenuating layer of thickness dx at depth x,

the change in the beam intensity dI in dx is propor-

tional to the intensity I at that depth x and the thickness

of the layer dx

dI =−μI dx (16.12)

with the proportionality constant μ, which is the lin-

ear attenuation coefﬁcient given in one per unit length.

Integration of (16.12) yields

= I

−μd

(16.13)

I –dI

Fig. 16.31 Attenuation law

Part D 16.2

Performance Control 16.2 Industrial Radiology 903

where I

is the intensity of the incident beam and I

is the primary intensity after penetrating material of

thickness d. Equation (16.13) is referred to as the at-

tenuation law. The linear attenuation coefﬁcient is given

by the sum of the interaction coefﬁcients for each of the

various processes mentioned above

μ =τ +σ

+π. (16.14)

Here τ is the attenuation coefﬁcient due to the photo-

electric effect, σ

that due to scattering, and π that due

to pair production.

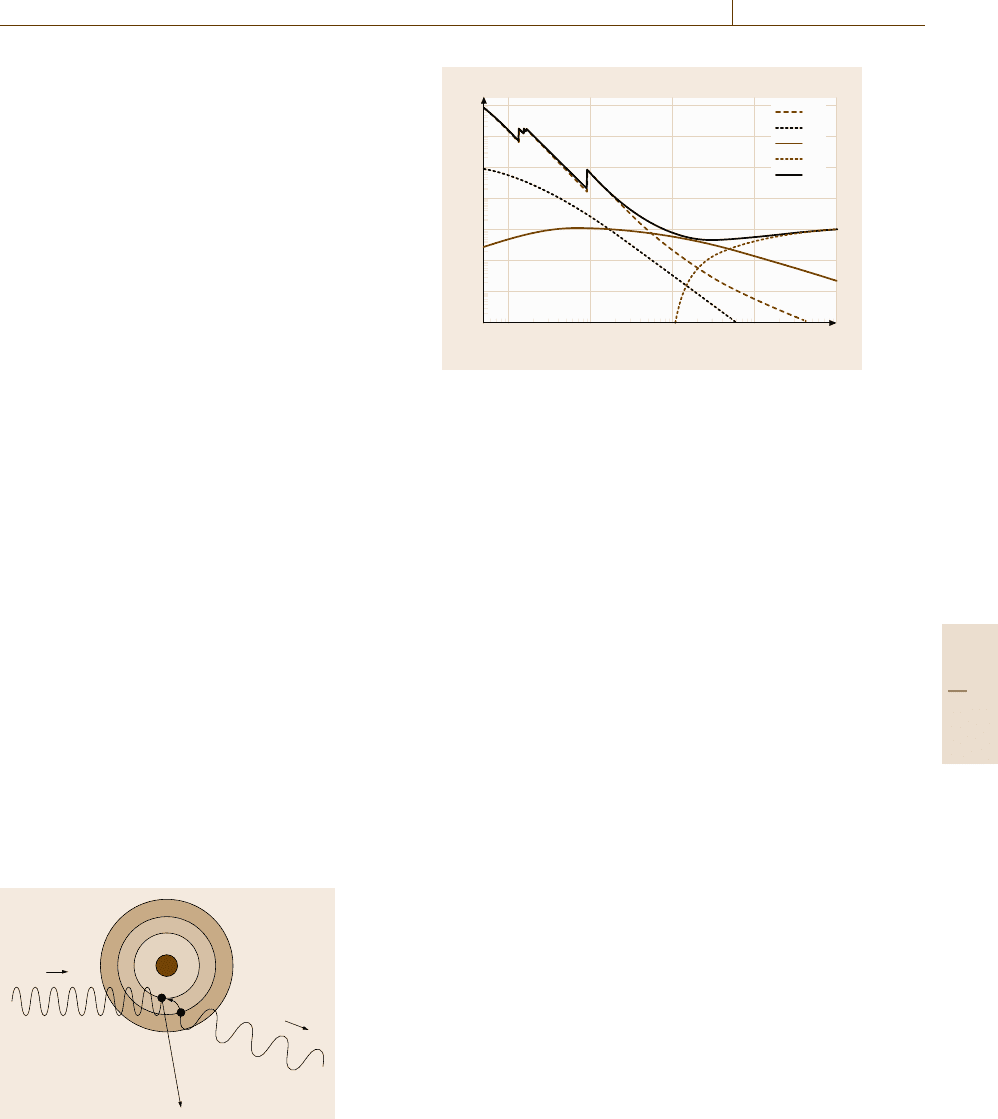
Photoelectric Effect. If a photon of energy E trans-

fers its total energy to an electron in some shell of

an atom, the process is called the photoelectric ef-

fect (Fig. 16.32). The energy of the photon can be

sufﬁcient to lift an electron from an inner to an outer

shell or to remove the electron completely and to ionize

the atom. In the second case, the photoelectron obtains

a kinetic energy given by the difference between the

photon’s energy and the binding energy of that partic-

ular electron. As the energy of the photon increases

absorption becomes possible by inner shell electrons.

When the energy of the photon reaches the binding en-

ergy of a particular shell of electrons the absorption

coefﬁcient increases abruptly because more electrons

are available for interaction. The energy at which this

sharp increase occurs is called an absorption edge,

which is characteristic for every atom. Otherwise the

absorption coefﬁcient decreases with increasing photon

energy. The energy dependence of the linear absorption

coefﬁcient for lead is shown in Fig. 16.33. As secondary

effects, recombination processes within the electron

shell yield either x-ray ﬂuorescence (Fig. 16.32)orthe

emission of Auger electrons.

MLK

K–X

–

Fig. 16.32 Photoelectric interaction of an incident photon

with an orbital electron may yield x-ray ﬂuorescence due to

recombination of electrons from a higher to a lower orbital

μ (cm

–1

)

–3

hv (MeV)

L edge

10.10.01 100

–2

–1

Fig. 16.33 Linear attenuation coefﬁcient μ for lead as

a function of energy hν: τ photoelectric effect, σ

Rayleigh

scattering, σ

Compton scattering, and π pair production

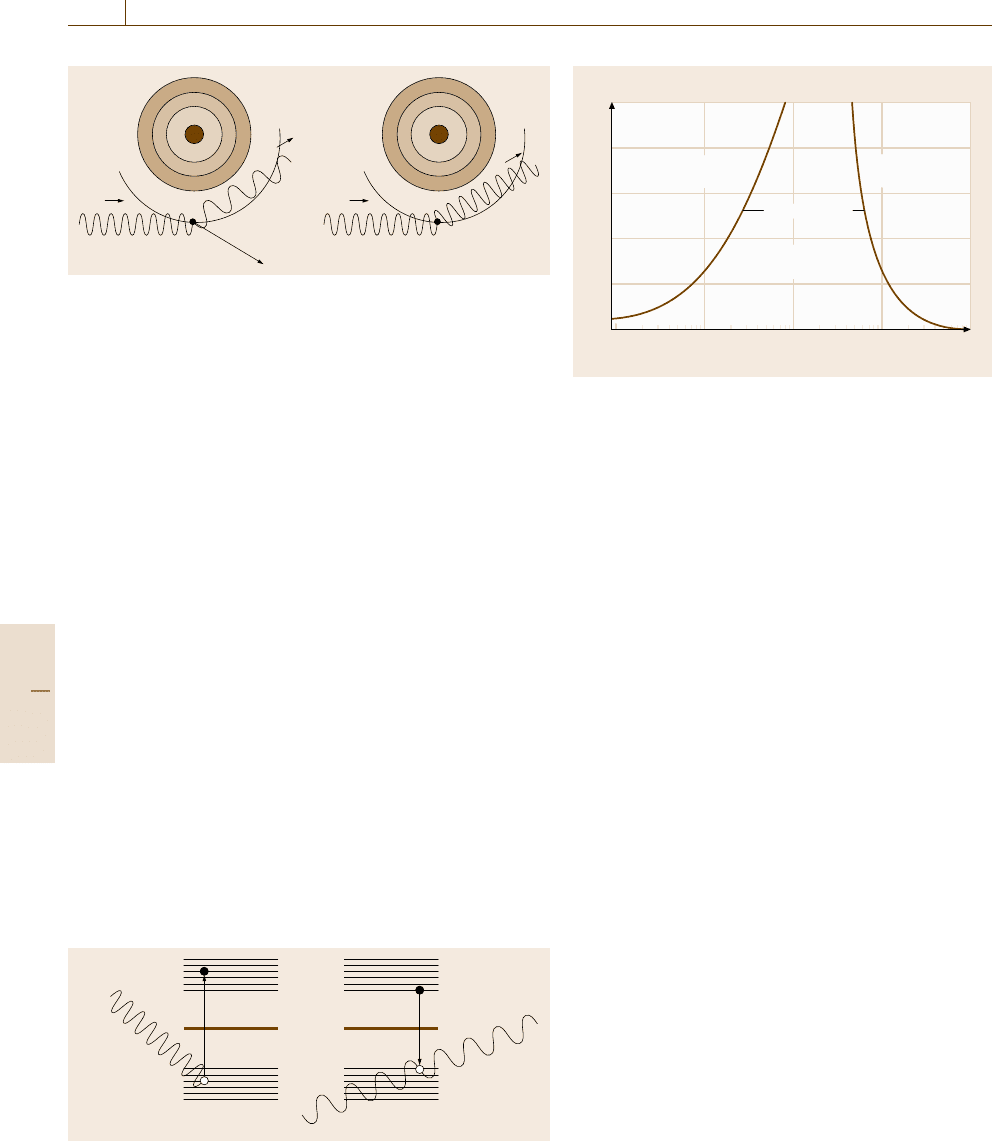
Scattering of Photons. Scattering can be incoherent,

which is known as Compton scattering, or coher-

ent, which is called Rayleigh scattering (Fig. 16.34).

Whereas a photon transfers its total energy to an or-

bital electron while undergoing an absorption event, it

loses no or only a part of its energy and is redirected if

a scattering event occurs.

The analysis of the Compton process shows that

the energy of the scattered photon E



is always less

than that of the primary photon E > E



. The remain-

ing energy is transferred to the struck electron as kinetic

energy. The energy shift predicted depends only on the

scattering angle θ and not on the nature of the scatter-

ing medium. The larger the scattering angle the larger

the energy shift observed. The relationship between the

scattering angle and the energy shift can be found from

the conservation of energy and momentum during the

collision when assuming particle properties of the pho-

ton. The scattering of a photon by a free electron is

described by the Klein–Nishina formula, providing an

accurate prediction of the differential cross section with

respect to the solid scattering angle. If considering elec-

tron binding effects the Klein–Nishina formula has to be

corrected by the incoherent scattering function, which

decreases the free-electron cross section in the forward

direction, for low energies E, and for high atomic num-

bers Z. The linear Compton coefﬁcient for lead can be

found in Fig. 16.33. In general it decreases with the pho-

ton energy, starting at an energy characteristic of the

material.

The coherent or Rayleigh scattering involves no en-

ergy loss of the photon upon being scattered by an

Part D 16.2

904 Part D Materials Performance Testing

M... L K M... L K

hv'

–

Fig. 16.34 Scattering effects: Compton scattering in which an in-

cident photon ejects an electron and a lower-energy photon (left);

Rayleigh scattering of a photon without energy loss

atom. It is only a photon process that does not produce

electrons. The angle distribution for coherent scatter-

ing of a photon by a free electron does not depend on

the photon’s energy and is given by the Thomson for-

mula, which is equivalent to the Klein–Nishina formula

at zero energy. To take account of electron binding ef-

fects, the Thomson formula has to be corrected by the

coherent atomic form factor. It yields a strong forward

directionality of Rayleigh scattering, which increases

with the photon energy. Rayleigh scattering occurs only

for soft radiation for which the binding energy of the

electrons in their atomic shell is important. It is most

important for elements of low atomic number Z and

high photon energies E. The Rayleigh cross section

decreases with energy (compare Fig.16.33). The contri-

bution of this type of scattering to the total attenuation

coefﬁcient is never greater than about 20%.

Pair Production. If the photon energy exceeds double

the electron mass of rest, i. e. if E = hν>1.022 MeV,

the photon is converted in the electrical ﬁeld of the

nucleus into an electron and a positron. This process

is called pair production (Fig. 16.35). Photons with

lower energy are not able to produce an electron–

positron pair. The photon energy that exceeds the

hv >2m

+ m

– m

= m

Fig. 16.35 Pair production (left) and positron–electron annihilation

(right)

100

h (Mev)

0.01 0.1 1 10

Photoelectric effect

dominant

Pair production

dominant

Compton effect

dominant

τ = σ

= π

Fig. 16.36 Relative importance of photon interactions

needed minimal energy for producing an electron–

positron pair appears as the kinetic energy of the pair.

The probability of occurrence of this process increases

approximately logarithmically with the energy above

the threshold value and then levels off for extremely

high photon energies (compare Fig. 16.33). The pro-

duced pair looses its kinetic energy within a very

short time of about 10

−12

s. The remaining resting

electron positron pair has a lifetime of about 10

−9

before annihilation. As a result two gamma photons

are emitted in opposite direction with energy of ex-

actly 511 keV.

As seen in Fig. 16.33, different attenuation mech-

anisms are dominant at different energies. The pho-

toelectric absorption is the dominant effect for lower

energies, whereas Compton scattering becomes impor-

tant for medium photon energies. For higher energies

pair production is the most probable interaction mech-

anism. Figure 16.36 shows the relative importance of

the different photon interactions with matter. The lines

show the values of the atomic number Z and the en-

ergy for which the two neighboring effects are of equal

importance.

Image Quality

The image quality is the characteristic of a radiographic

image that determines the degree of detail it shows. It

is inﬂuenced by a large variety of inﬂuencing factors

originating in the inspected object (material, thickness),

the radiation source (radiation quality), the imaging sys-

tem (detector properties), and geometry (focal spot size,

source-to-object distance, object-to-detector distance).

Image quality can be measured by image quality indi-

cators (IQI).

Part D 16.2

Performance Control 16.2 Industrial Radiology 905

Δd

Fig. 16.37 Image formation

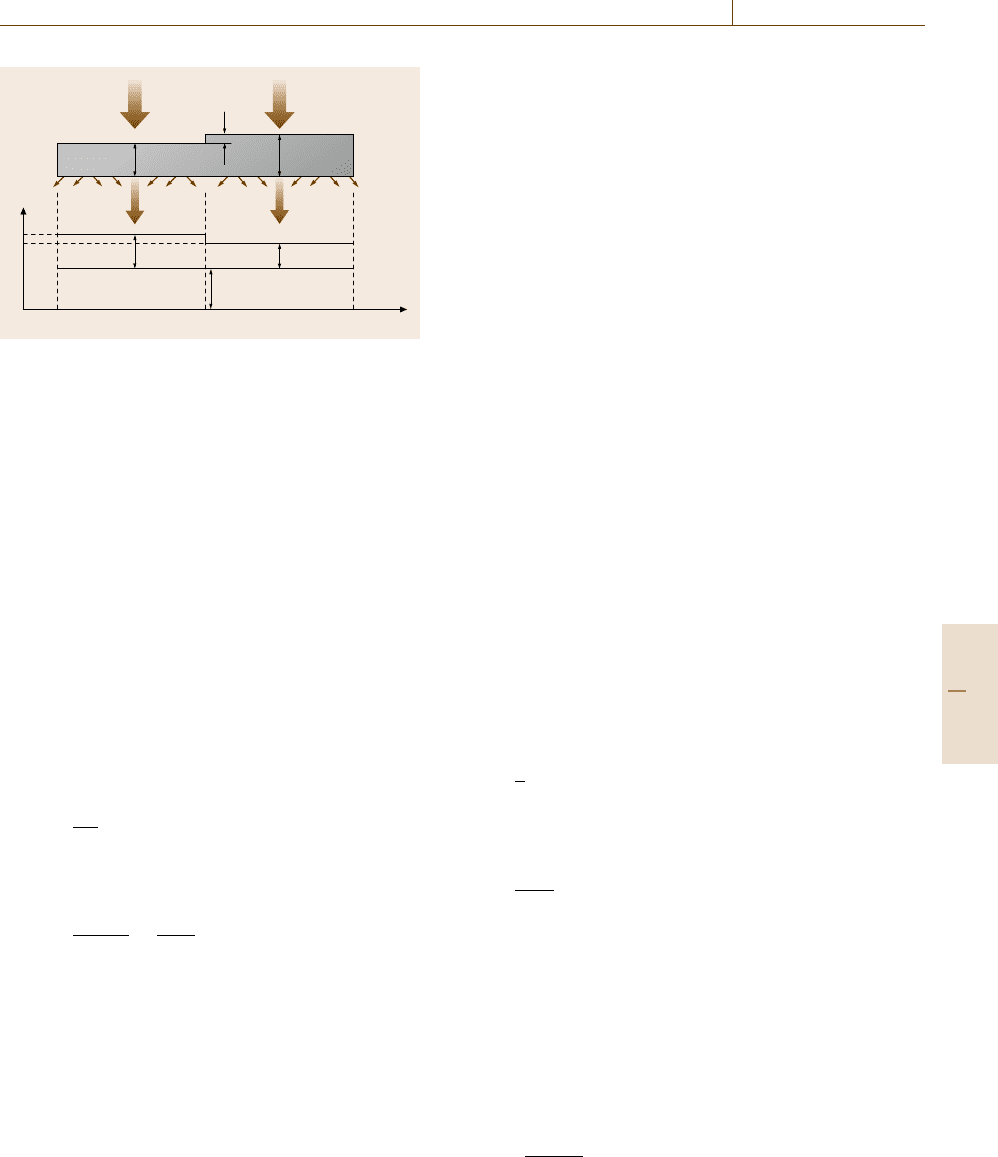
Contrast. The formation of a radiographic image can

be easily explained in terms of a simple step ob-

ject (Fig. 16.37). The intensity or density difference

seen between two thicknesses at a given detection inten-

sity I or density in an object on a radiograph represents

the radiographic contrast in the image (approach for

small thickness differences)

= I

−I

(16.15)

with the intensities I

and I

after penetrating a ma-

terial of thickness d

and d

, respectively. Introducing

= I

as a reference primary intensity, a linear rela-

tion follows between the absolute contrast ΔI and the

thickness difference from the attenuation law (16.13)

ΔI = I

μΔd . (16.16)

For the interpretation of radiographs the relative con-

trast with which an indication is imaged is important

ΔI

(16.17)

where I = I

gives the total intensity. For small

thickness differences, it follows from using (16.16)that

μΔd

1 +k

Δd = C

Δd (16.18)

with the scattering ratio k = I

and the speciﬁc

contrast C

= μ/(1 +k). Hence, the relative and the

speciﬁc contrast increase with the attenuation coefﬁ-

cient, but decrease with increasing scattering ratio and

increasing material thickness. As result, high-energy

radiation yields higher contrast for large thicknesses

(steel > 50 mm; aluminum > 100 mm) than lower en-

ergy radiation because the increase of contrast due to

decreasing scatter ratio is larger then the decrease of

contrast due to decreasing attenuation coefﬁcient. This

effect can be achieved either by using higher-energy

sources (increase of kilovoltage for x-ray tubes, applica-

tion of gamma radiation) or by using ﬁlters to increase

the quality of radiation.

Noise and Granularity. The perception of any indica-

tion depends on the contrast-to-noise ratio (CNR). The

image noise is measured quantitatively as the standard

deviation of the mean value of the intensity or den-

sity in a projected area of constant object thickness.

Density ﬂuctuations are described as the granularity of

ﬁlm systems. The visual impression is the graininess.

The term noise is used dominantly in digital radiol-

ogy. The CNR increases with the square root of the

required exposure time of a ﬁlm system or digital de-

tector. This is the reason why slow ﬁlm systems provide

higher contrast sensitivity than fast ones. The human

perception depends on the shape of the object. Lin-

ear edges, cracks and wires are already recognizable

at CNR > 0.7. For the perception of small volumetric

objects or ﬂaws (e.g. balls, pores) the required CNR

is > 2.5.

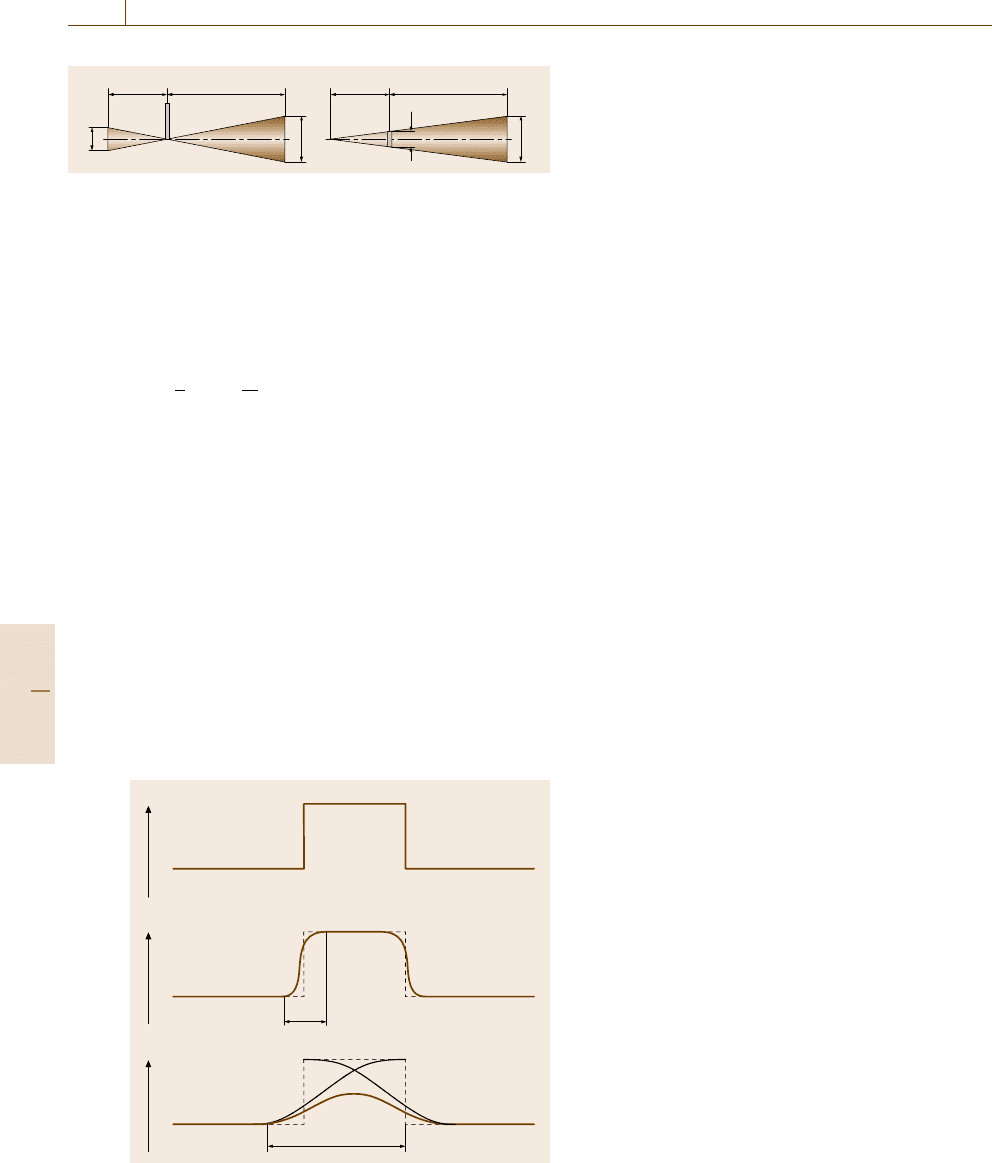
Unsharpness. The sharpness of the outline of an im-

age is directly affected by the geometrical unsharpness

generated by the source size, the source-to-object and

the object-to-detector distances (SOD, ODD), and the

inherent unsharpness u

of the detector.

The blurring of an edge image due to a ﬁnal focal

spot size S is deﬁned by the geometrical unsharpness

(Fig. 16.38, left)

S =(M −1) S (16.19)

with the magniﬁcation factor M according to Fig. 16.38

(right).

M =

a +b

. (16.20)

Additionally the detector system contributes to the

system unsharpness. Due to the properties of the detec-

tor an additional edge blurring is observed. In the case

of ﬁlm radiography there can be drawbacks, e.g. to the

use of intensifying screens and to the scattering of pho-

tons or electrons in the ﬁlm emulsion. This contribution

is called inherent unsharpness u

The total unsharpness u

observed in a radiograph

when neglecting the effect of motion during exposure

can be approximated by



. (16.21)

Part D 16.2

906 Part D Materials Performance Testing

bab

Fig. 16.38 Geometrical unsharpness (left) and magniﬁcation (right)

The optimal geometry for taking radiographs with

minimum effective unsharpness (u

divided by mag-

niﬁcation) can be determined if the inherent and

geometrical unsharpness are chosen equivalent. From

this condition the optimal ratio of the SOD and SDD

follows





opt

. (16.22)

As long as the projection d



= Md of an object of size

d is larger then the total unsharpness the contrast of

the indication is not decreased and follows (16.16). If

the unsharpness exceeds d



a decrease of the indication

contrast is observed (compare Fig. 16.39).

Image-Quality Indicators (IQI). Image-quality indica-

tors are standardized devices consisting of a series of

elements of graded dimensions, which enable a measure

of the image quality to be obtained. IQIs are usually in-

cluded in every radiograph to check on the adequacy

of the radiographic technique. The elements of IQIs are

commonly wires and steps or plates with holes. IQIs

together with their usage are described in detail in the

< d'

> d'

Fig. 16.39 Inﬂuence of unsharpness to image contrast

European standards EN 462 part 1–5 and, in the USA,

standards ASTM E 747, E 1025, and E 2002.

Wire-type IQIs consist of wires that are arranged

by diameter, all with the same length (Fig. 16.40a). The

wire material is chosen to match the material of the in-

vestigated object. It measures the thickness resolution

of the radiographic technique.

The European step hole IQI system is based on

a series of steps of different thickness d and holes of

diameter equal to the step thickness (Fig. 16.40b). The

material is chosen to match the material of the inves-

tigated object. The image-quality value is given by the

number of the smallest hole that is visible on the radio-

graph.

The American plate hole IQI (ASTM E 1025)

consists of a small rectangular or circular piece of

metal usually containing several holes, the diam-

eters of which are related to the thickness of the

plate. The ASTM penetrameter contains three holes

of diameters T,2T,and4T, where T is the thick-

ness of the plate. The material is again chosen

to match the material of the investigated object.

The IQI gives the equivalent penetrameter sensi-

tivity (EPS) in terms of contrast resolution, which

is a measure for the minimal resolvable thickness

difference together with the minimal resolvable de-

tail inﬂuenced by the total unsharpness (compare

Fig. 16.39).

Duplex wire indicators (Fig. 16.40c) are used when

it is necessary to evaluate and measure the total image

unsharpness (spatial resolution) separately from con-

trast sensitivity measurements. Every element consists

of two circular wires of certain diameter, which equals

the spacing between the wires. Highly attenuating ma-

terial, such as tungsten and platinum, is chosen for the

wires. The largest element without identifying space be-

tween the images of the two wires is taken as the limit

of discernibility.

16.2.2 Particle-Based Radiological Methods

X- and γ -ray radiography are the most important

and well-accepted methods in industry. Neverthe-

less there also exist other methods that are based

on the attenuation of neutrons, positrons and elec-

trons. Neutron radiography is dominant in the air-

craft and military industries and in research. The

attenuation of neutrons in materials follows other

laws than x-ray and γ -radiography. Figure 16.41

shows the different attenuation coefﬁcients for thermal

neutron- and x-radiography as function of the ele-

Part D 16.2

Performance Control 16.2 Industrial Radiology 907

ment number in the periodic system. Materials which

contain the elements H, B, Li, Cd, Gd, Sm and Eu at-

tenuate neutrons much more than construction metals

as Al, Fe, Co and Ni. This enables the radiography of

organic components in metallic encapsulation such

as rocket motors and ammunition with high con-

trast of structures and ﬂaws of the organic materials

(e.g. explosives). Moisture in aircraft components

can also be detected at high contrast. More de-

tails about n-radiography as well as positron and

electron radiography can be found in the ASNT hand-

book [16.21].

16.2.3 Film Radiography

Radiography in medicine and industry is carried out un-

der different considerations. Medical applications have

to be performed with minimum exposure dose for the

patient. Therefore, the typical ﬁlm system consists of

ﬂuorescence screens and ﬁlm. The optical ﬁlm den-

sity is typically between 1 and 2. Industrial applications

for nondestructive testing (NDT) generally use ex-

posure dose values which are 10–100 times higher.

The resulting NDT image quality is characterized by

higher sharpness and contrast sensitivity. Industrial ra-

diographic ﬁlms contain usually a higher silver content,

which allows higher optical density (blackening) to

be obtained. NDT ﬁlms are applied for density val-

ues of 2–4.5. Special high-brightness viewing stations

are required. Medical viewing equipment is not suf-

ﬁcient. NDT ﬁlm systems consist of double-layered

ﬁlms with thin lead screens at the front and back side.

The x-rays penetrate the ﬁlm and expose the front and

back sides. The lead screens convert x-rays to fast elec-

trons, which expose the ﬁlm more efﬁciently than the

x-rays. These screens are used for intensifying the ex-

posure, in particular for high-energy x-rays. Since the

lead screens convert the photons to electrons instead of

light, the exposed radiographs are not blurred by scat-

tered light. Radiographs taken with ﬂuorescence screens

have an unsharpness of 0.2–0.4 mm, depending on the

screen thickness and x-ray energy. Film lead screen

systems have an unsharpness of 30 μm to a few hun-

dred microns, depending on the screen thickness and

energy.

NDT ﬁlm systems are classiﬁed corresponding to

the standards ISO 11699, EN 584, JIS K 7627 and

ASTM E 1815. The classiﬁcation requires the user to

select the ﬁlm type and the developer as well as the

certiﬁed developer temperature and immersion time to

prove conformity with the standards.

a) b)

Tungsten Platinum

Spacing

5 mm

Spacing

4 mm

Spacing

3.5 mm

15 mm

4 mm

Wire diameter d equals

spacing between wires

Enlarged view of wire pair

Fig. 16.40a–c Selection of image-quality indicators (IQI), de-

scribed in European standards: (a) wire IQI; (b) step hole IQI;

Mass absorption coefficient (μ/ρ)

Atomic number

10008070605040302010 90

–1

–2

–3

–4

Neutrons (λ =1.08 A)

X-rays (λ =0.098 A)

Fig. 16.41 Comparison of mass absorption coefﬁcients for the ele-

ments for both x-ray and thermal neutrons. (after: Thewlis, Argonne

National Laboratory)

Part D 16.2