Czichos H., Saito T., Smith L.E. (Eds.) Handbook of Metrology and Testing

Подождите немного. Документ загружается.

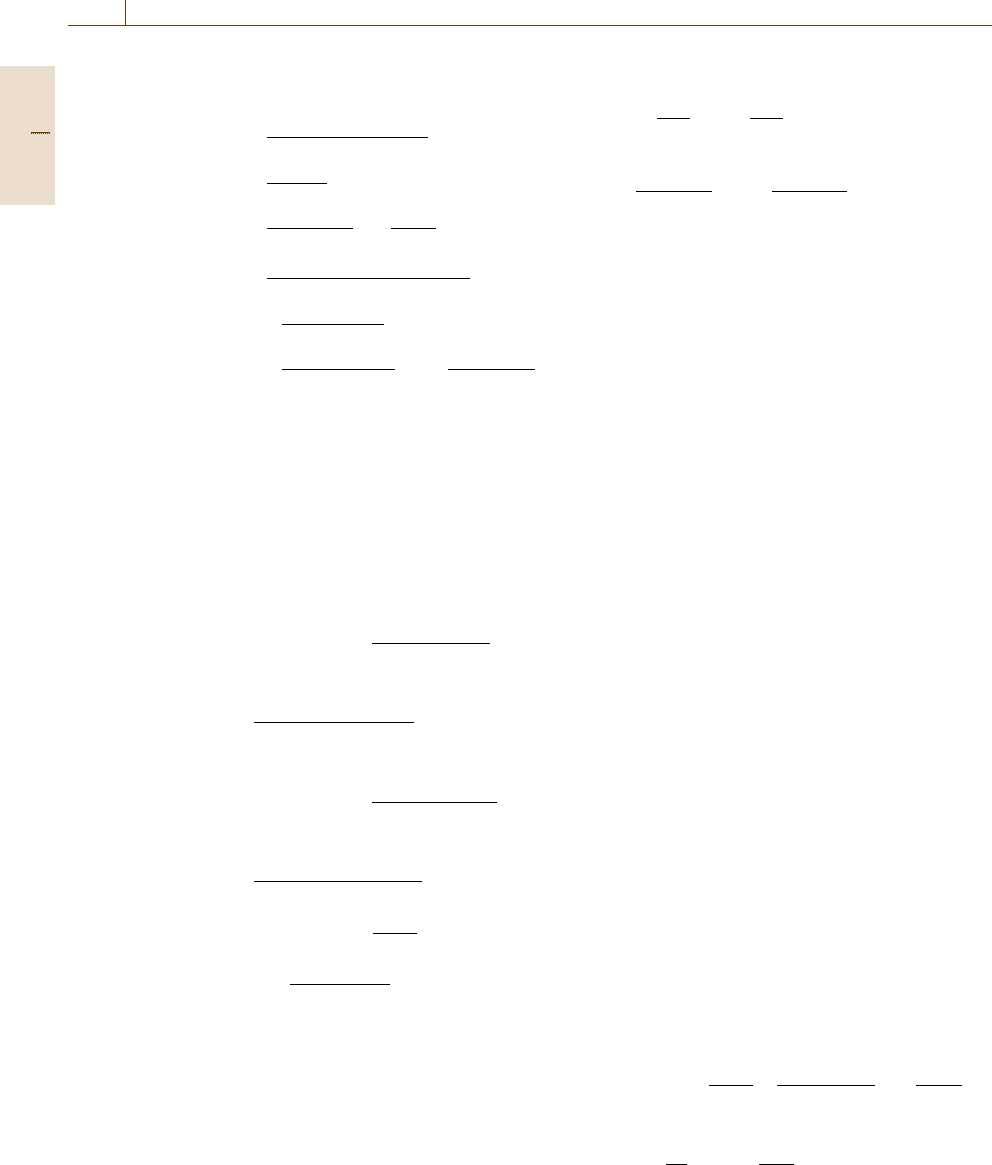
678 Part D Materials Performance Testing

potential E

exp

−



0,A+

−αzFΔφ





exp

αzFΔφ



exp

−αzFΔφ

exp

αzFE

, (12.22)

−

0−

exp

−



0,A−

+(1 −α)zFΔφ





0−

exp −

(1 −α)zFΔφ



0−

exp −

(1 −α)zFΔφ

exp −

(1 −α)zFE

(12.23)

The introduction of (12.22, 12.23)into(12.19) yields

(12.24). For the conditions of electrochemical equi-

librium, i. e. for E = E

and i = 0, one obtains the

expression for the exchange current density i

(12.25). Introducing the overpotential η = E −E

and

(12.25)fori

in (12.24) one obtains the Butler–Volmer

equation (12.26)

i =nFk



c(Red) exp



αzF(E +Δφ

)



−nFk



0−

c(Ox) exp



−

(1 −α)zF(E +Δφ

)



(12.24)

for E = E

, i = 0 ,

=nFk



c(Red) exp



αzF(E

+Δφ

)



=nFk



0−

c(Ox) exp



−

(1 −α)zF(E

+Δφ

)



, (12.25)

i =i

−



exp



αzFη



−exp



−(1−α)zFη



. (12.26)

For large positive overpotentials η  RT/F the ca-

thodic current density may be neglected and for large

negative overpotentials with η  RT/F the anodic

current density is vanishingly small. Taking the log-

arithm of (12.26) one obtains the η-log i equations,

(12.27)and(12.28), for both cases. The appropriate

semi-logarithmic presentation yields the so-called Tafel

plot

η =−

αzF

ln i

−

αzF

ln i

=a +b log i

(12.27)

η =

(1 −α)zF

ln i

−

(1 −α)zF

−

=a +b log

−

. (12.28)

Figure 12.11 gives an example of a dimensionless

log

−η presentation for different charge-transfer

coefﬁcients α with an anodic and a cathodic branch.

For α = 0.5 both branches are symmetrical to each

other and for α = 0.5 they are asymmetric. The meas-

ured current densities i deviate from the Tafel lines

for η ≤0.1V and η ≥−0.1 V due to the inﬂuence of

the corresponding counter-reaction. Extrapolation of

the Tafel lines meet at the equilibrium potentials with

η = 0, i = i

and log

=0. The constants a and b

of a Tafel plot are important kinetic parameters for an

electrode process. The b factor contains the value of

α and constant a the exchange current density i

.Ac-

cording to (12.22–12.25) i

depends on the activation

energy and the electrochemical reaction order for those

species that inﬂuence the rate law. The same equations

(12.22–12.28) hold for redox reactions as well as for

anodic metal dissolution and cathodic metal deposition,

when the concentrations of the cations are introduced.

The evaluation of the kinetics of a redox process or

metal dissolution requires Tafel plots, which then yield

data from the slope and the intersection with the ordi-

nate.

An alternative approach requires the determination

of the slope of the polarization curve at E = E

only.

For small overpotentials the development of the i-η re-

lation (12.26) in a MacLaurin series with only the linear

terms for η yields (12.29). Its reverse slope for η →0V

yields the charge-transfer resistance R

of (12.30). Ac-

cording to this equation only the reciprocal slope of the

polarization curve has to be determined for η →0toget

the exchange current density i

. Thus the determination

of the total polarization curve is not required. A similar

situation holds for the rest potential E

when two differ-

ent reactions compensate each other, as will be shown

in the following section (12.36, 12.37)

i =i



1 +

αzFη

−

[(1 −α)zFη]



zFη

(12.29)



dη



η→0

zFi

. (12.30)

Part D 12.2

Corrosion 12.2 Conventional Electrochemical Test Methods 679

12.2.7 Elementary Reaction Steps

in Sequence,

the Hydrogen Evolution Reaction

Electrochemical processes often consist of a sequence

of elementary reaction steps. This situation is treated

similarly to the general rules of chemical kinetics. The

slowest step in a sequence determines the total rate. Any

preceding process is submitted to stationary conditions

or chemical equilibrium may even be established. Any

fast following step does not affect the rate of the over-

all process. In this section the possible mechanisms of

cathodic hydrogen evolution and its inﬂuence on the

rate equation and cathodic current density are described.

This relatively complicated electrochemical process is

presented as an example for the treatment of a sequence

of elementary reaction steps. Furthermore it is a very

important reaction for corrosion processes.

Two possible reaction paths are discussed, the

Volmer–Tafel and the Volmer–Heyrovski mechanism.

In both cases the process starts with the oxidation of

hydrogen ions to atoms H

adsorbed at the electrode

surface according to the Volmer reaction of (12.31). The

log | i |/i

log | i

–

|/i

log i

(1– a)= 0.75

a =0.75

AnodeCathode

0.5

0.15–0.15 –0.1 0.1–0.05 0.05

–2

–1

0.5

0.25

(V)

Fig. 12.11 Tafel plot for a charge-transfer-controlled reac-

tion and its dependence on the charge-transfer coefﬁcient

α (after [12.35])

following Tafel reaction (12.32a) involves the combina-

tion of two H

to H

2,ad

, which is then ﬁnally transferred

to the electrolyte by desorption and diffusion to the

bulk electrolyte. At high negative overvoltages hydro-

gen formation is fast enough to form gas bubbles. An

alternative is the Heyrovski reaction (12.32b), a sec-

ond charge-transfer step which involves the reduction

of a hydrogen ion in the vicinity of H

to from H

2,ad

that then again desorbs and diffuses to the bulk.

Volmer reaction: H

−

→H

; (12.31)

Tafel reaction: H

→H

2,ad

; (12.32a)

Heyrovski reaction: H

−

→H

2,ad

;

(12.32b)

Desorption: H

2,ad

→H

. (12.33)

With the Volmer reaction as a rate-determining step

one obtains for the cathodic current density of hy-

drogen evolution i

the Butler–Volmer equation as

described by (12.26). For sufﬁciently large cathodic

overvoltages i

is described by (12.28). A Tafel

plot of (12.28) yields, with z = 1andα = 0.5,

a slope b =

dη

dlog

RT2.303

(1−α)F

0.059

0.5

=−0.120 V. Fig-

ure 12.12 presents the Tafel plot for cathodic hydrogen

evolution at various metals [12.35]. From the slope

1/b of this log

–η presentation one obtains for most

metals a factor b =−0.12 V. The Tafel lines for the met-

als are shifted relative to each other, which proves the

strong inﬂuence of the kind and surface condition of the

electrode materials on the electrode kinetics. The paral-

lel shift of these lines is caused by the speciﬁc values of

the exchange current density i

H,0

for the different met-

als, i. e. of the constant a of (12.28). Pt is a metal with

a small overvoltage whereas Pb and Hg have large over-

voltages. The very fast kinetics on Pt are very useful

for water electrolysis to produce hydrogen as fuel with

optimized energy input. On the contrary Pb and Hg elec-

trodes are well suited to the suppression of hydrogen

evolution when other cathodic reactions are of interest,

such as the reduction of organic compounds or electrol-

ysis of NaCl or KCl solutions, which yield Cl

gas at

the anode and K or Na amalgam at the cathode. Hg elec-

trodes are also well suited for polarography. Here again

the large overvoltage suppresses hydrogen evolution

and permits the analysis of cations of very reactive met-

alssuchasZn

and Cd

by their cathodic reduction.

If the Heyrovski reaction of (12.32b) is the rate-

determining step it will lead to the kinetic equa-

tion (12.34). Here Θ

is the surface coverage of hydro-

gen atoms which is proportional to their surface concen-

tration. Assuming electrochemical equilibrium for the

Part D 12.2

680 Part D Materials Performance Testing

Current density log

(A/cm

)

–1

–2

–3

–4

–5

–6

–7

–8

–9

–1.6

NiNi

AgHg

Pt (plat.)

+2e

–

(2H

O+2e

–

+ 2OH

–

)

–0.4–0.6–0.8–1.0–1.2–1.4 –0.2 0

Overvoltage η (V)

Fig. 12.12 Tafel plot of cathodic

hydrogen evolution for different

electrode metals (after [12.35])

preceding Volmer reaction one obtains from the related

Nernst equation (12.35) which allows the replacement

of Θ

with (12.36)in(12.34). Equation (12.37)then

contains c

), i. e. the electrochemical reaction or-

der of H

is 2. It also contains a modiﬁed exponential

term. Replacing E = E

+η one obtains the related

Tafel (12.38) which yields with α =0.5 a slope b =0.40

=−k

−





exp



−

(1 −α) F



(12.34)

E = const







, (12.35)

=const c





exp



−



, (12.36)

=−k

−





exp



−

(

2 −α

)



=−k

−





exp



−

(

2−α

)



+η





(12.37)

η =

RT2.303

(

2 −α

)

log



0,H



−

RT2.303

(

2−α

)

log

=a +b log

. (12.38)

Part D 12.2

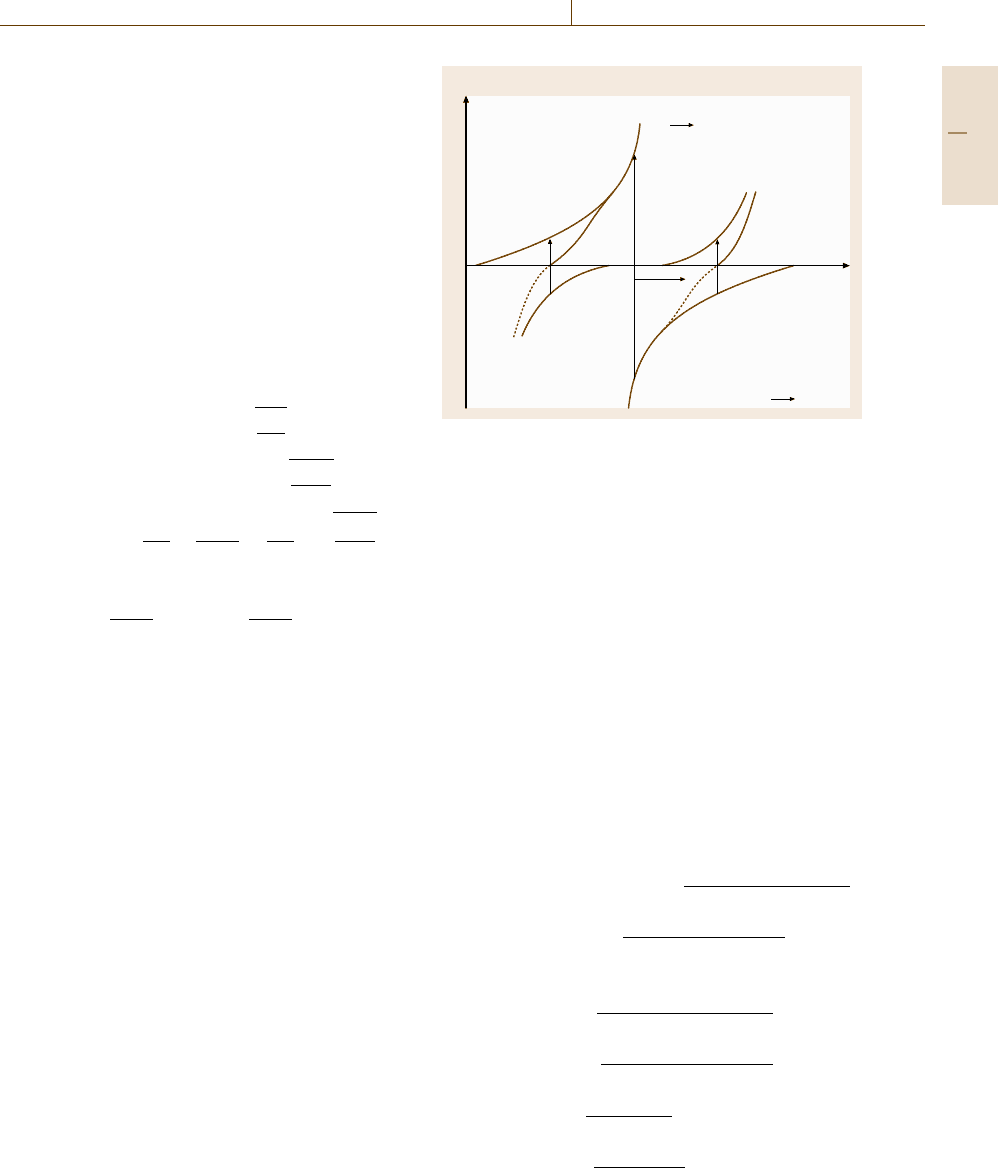
Corrosion 12.2 Conventional Electrochemical Test Methods 681

If the Tafel reaction (12.32a) is the rate-determining

step one starts with (12.39)and(12.40)fori

and

and i

0,H

and Θ

H,eq

respectively. Assuming electro-

chemical equilibrium for the Volmer reaction (12.31)

yields the Nernst equation for this charge-transfer step

and consequently (12.41a) for the electrode potential E

and for the overvoltage η. η is thus a consequence of

the varying surface coverage Θ

with i

. For this dis-

cussion diffusion control of H

ions from the bulk

to the electrode surface is excluded and therefore the

same concentration c(H

) is present within the bulk

and at the electrode–electrolyte interface. In conse-

quence the Tafel plot according to (12.40) yields a slope

dη/dlogi

=b =−0.29 V if the Tafel reaction is the

rate-determining step

|=kFΘ

,Θ



, (12.39)

H,0

|=kFΘ

H,eq

,Θ

H,eq



H,0

, (12.40)

E −E

=η =

H,eq



H,0

;

(12.41a)

η =

0.059

log |i

H,0

|−

0.059

log |i

=a +b log i

. (12.41b)

12.2.8 Two Different Reactions

at One Electrode Surface

The corrosion rate may be ruled by metal dissolution or

by a compensating cathodic reaction of a redox system.

Metal dissolution by hydrogen evolution or oxygen re-

duction are important examples. In acidic electrolytes

hydrogen evolution is the favored counter-reaction for

dissolution of reactive metals such as iron and will be

discussed as an example. The equilibrium potential of

the hydrogen electrode E

=−0.059 pH is much more

positive than the standard potential E

=−0.409 V for

the Fe/Fe

electrode, which is a necessary require-

ment for an efﬁcient metal dissolution. However in

addition the kinetics of both processes determine the

shape of their polarization curves and thus have a strong

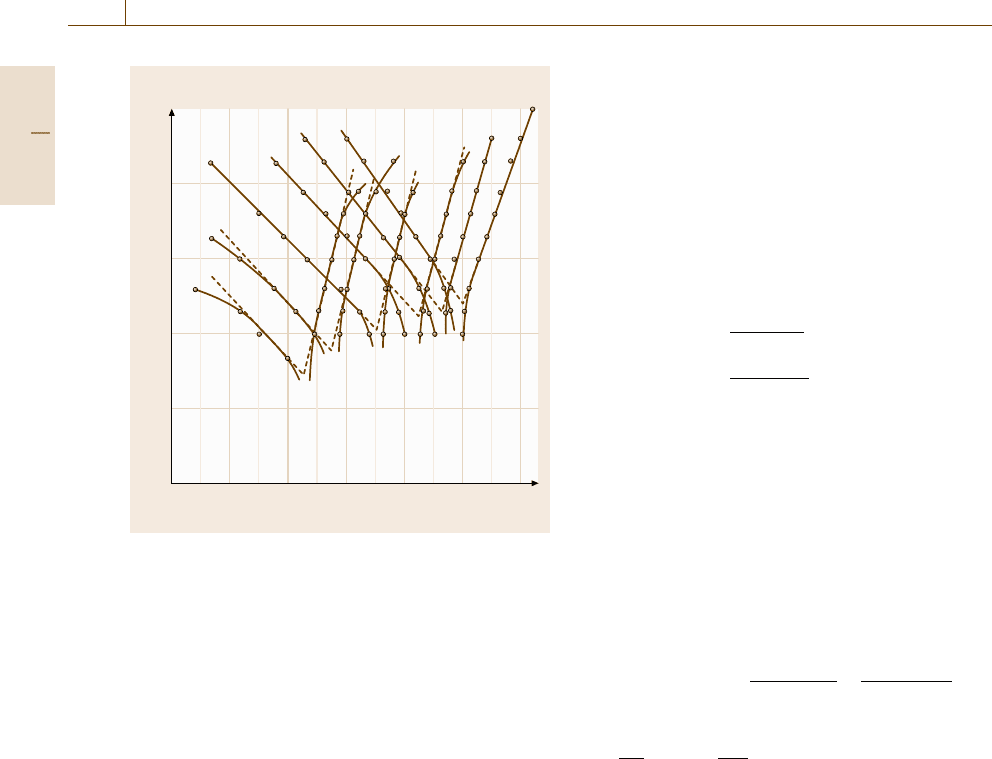
inﬂuence on the overall process. Figure 12.13 presents

schematically the anodic and cathodic reactions of both

electrodes in the vicinity of their equilibrium potentials

(Me/Me

)andE

). The rest potential E

is found between both values where anodic metal dis-

solution and cathodic hydrogen evolution compensate

i (A/cm

)

E (H

)

E (Me/Me

)

0, red

0, Me

E (V)

+ z e

–

2z H

+2z e

–

z H

Fig. 12.13 Schematic diagram of metal dissolution and hy-

drogen evolution as cathodic counter-reaction with rest

potential E

each other. E

is sufﬁciently distant from both equilib-

rium potentials so that only Fe dissolution and hydrogen

evolution have to be taken into account. For a positive

polarization π = E − E

> 0 metal dissolution exceeds

hydrogen evolution with a total anodic current i and

for the opposite case hydrogen evolution is larger with

a total cathodic current i. Both partial reactions may be

described by a Butler–Volmer equation and their sum

leads to a similar expression (12.42) as discussed before

when opposite partial reactions of the same electrode

process compensate each other as described by (12.26).

For a vanishing total current density i,i.e.forπ = 0,

one obtains (12.43) for the corrosion current density i

Its application to (12.42) yields (12.44) which has a sim-

ilar form as (12.26)

i =i

0,Me

exp



F(E −E

0,Me

)



−i

0,H

exp



−

(1 −α

)F(E − E

0,H

)



(12.42)

0,Me

exp



F(E

−E

0,Me

)



0,H

exp



−

(1 −α

)F(E

−E

0,H

)



, (12.43)

i =i



exp



Fπ



−exp



−

(1 −α

)Fπ



. (12.44)

Part D 12.2

682 Part D Materials Performance Testing

–2

–3

–4

–5

–1

–6

–0.4–0.5–0.6–0.7–0.8–0.9 –0.3

–0.23

–0.90

32 33 38 40

0.40

1.63

2.95

pH = 4.0

Electrode potential E (V)

Current density (A/cm

)

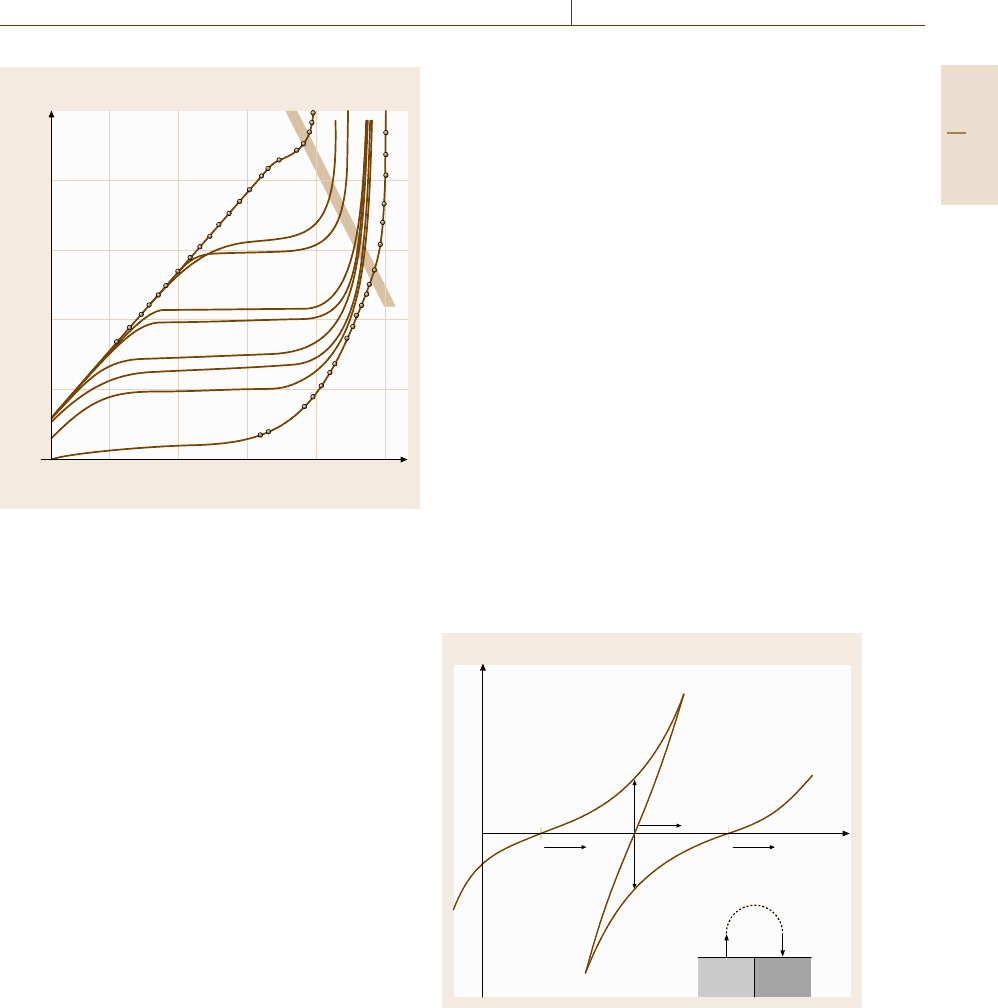
Fig. 12.14 Tafel plot for Fe

dissolution and hy-

drogen evolution of an Fe electrode in solutions

of H

/Na

mixtures: 0.482 M/1M pH 4.0,

0.00482 M/1M, pH 2.95, 0.0965 M/0.9M, pH 1.63,

0.75 M/0.75 M, pH 0.40, 2 M/0, pH −0.23, 5 M/0M,pH

−0.90 (after [12.36])

For large polarizations i. e. π  RT/α

F or

π  RT/(1 −α

)F the anodic or cathodic current den-

sity dominates the overall process, so that i equals the

ﬁrst or second term of (12.44), respectively. These con-

ditions yield (12.45)and(12.46), which describe Tafel

plots for metal dissolution and hydrogen evolution. The

extrapolation of the lines intersect at π = 0andE = E

with i =i

. An example for iron dissolution and hydro-

gen evolution is presented in Fig. 12.14 as a function

of pH [12.36]. With increasing pH the Tafel lines of

hydrogen evolution are shifted to negative potentials.

This is a consequence of the −0.059 pH dependence of

the equilibrium potential of the H

electrode, but

also of the decrease of the kinetics of H

evolution. At

pH 4.0 and 3.0 the start of diffusion control may be seen

by the deviation of the current density from the Tafel

line for large cathodic overvoltages. In addition Fe dis-

solution is pH-dependent; its Tafel lines shift to more

negative potentials with increasing pH. This is a con-

sequence of the aforementioned OH catalysis of iron

dissolution [12.34]. Iron dissolution occurs with a dis-

solution current density log i ∝ 1.5logc(O

−

). Thus the

electrochemical reaction order for OH

−

ions is 1.5, i. e.

log i increases by 1.5 orders when the pH increases by

one unit. Both effects lead to the observed negative shift

of E

with increasing pH but they compensate each

other partially with an only moderate decrease of the

corrosion current density i

at the rest potential. i

may

be determined by the evaluation of the Tafel lines but

also by a direct measurement of metal dissolution. The

related data may be obtained by analysis of the concen-

tration of metal ions within the electrolyte but also by

the weight loss of metal specimens. These independent

data should match each other

log i = log i

π for π>0 , (12.45)

log i = log i

−

(1 −α

π for π<0 . (12.46)

A third possibility uses the inverse polarization resis-

tance 1/R

=(di/dπ)

π→0

similar to the discussion of

the charge-transfer resistance of (12.30). The develop-

ment of (12.44) by a MacLaurin series for π →0 yields

(12.47)and(12.48) which may serve to determine the

missing kinetic parameters α

and α

. With known

charge-transfer coefﬁcients α one may determine i

Similar relations hold with z

Red

as a factor of the sec-

ond term of (12.47) for the case of other redox systems

such as the reduction of dissolved oxygen or Fe

ions

taking over the counter-reaction for metal dissolution

i = i



Fπ

(1 −α

)Fπ



(12.47)



dπ



π→0

[α

+(1 −α

)] . (12.48)

Hydrogen evolution by water decomposition is an

important cathodic process for neutral and alkaline solu-

tions. In these cases the concentration of H

ions is too

small to contribute to the cathodic reduction. Hydrogen

evolution by water reduction has a large overpoten-

tial and thus relatively negative potentials are required

to start this reaction. The cathodic polarization curves

for different pH merge at very negative potentials all

in one line because it is not the H

but the high and

pH-independent water concentration that enters the rate

equation for these conditions. Figure 12.15 compares

the hydrogen evolution on Fe in HCl solution with 4%

NaCl [12.37, 38]. In acidic electrolytes a linear part

for log i/E is found, corresponding to charge-transfer

control of H

reduction. The deviation in the vicin-

ity of E

is caused by compensating Fe dissolution.

At large cathodic polarization the current density enters

a plateau which is caused by diffusion control. Its value

Part D 12.2

Corrosion 12.2 Conventional Electrochemical Test Methods 683

Electrode potential E (V)

Current density (A/cm

)

–10

–2

–10

–3

–10

–4

–10

–5

–10

–6

–10

–7

–0.5–0.7–0.9–1.1 –0.3

4.11

3.69

2.91

2.69

2.19

1.98

1.42

2.42

pH = 5.26

Fig. 12.15 Hydrogen evolution on Fe in HCl+4% with pH

as indicated (after [12.37,38])

is proportional to c(H

). This situation with dominating

diffusion overvoltage will be discussed in Sect. 12.2.11.

Finally all cathodic current densities merge in one line

corresponding to hydrogen evolution by water decom-

position. No limiting current is achieved for very high

cathodic overvoltages due to the high water concen-

tration as reacting species of 55.56 M. For pH > 4no

hydrogen evolution by H

reduction is possible due

to its very small bulk concentration and the plateau of

a diffusion-limited process of H

reduction is missing.

12.2.9 Local Elements

The above discussion assumes a homogeneous elec-

trode with the same reactivity all over the surface. If

an electrode is composed of physically or chemically

different areas A and B with varying electrochemical

activity their cathodic and anodic reaction rates and re-

lated current densities i

and i

will follow the same

behavior as described above. i

and i

are the po-

larization curves that could be measured for the pure

surfaces A and B. They differ from each other in shape

and position on the potential scale and thus have dif-

ferent rest potentials E

R,A

and E

R,B

. The combination

of A and B in one surface causes a potential shift of

A and B to a new value E

R,AB

in between both. At

R,AB

the anodic current i

on A and a cathodic current

on B will compensate each other. As a consequence

a net current |i

R,AB

) |=|i

R,AB

) | will ﬂow from

A to B within the electrolyte and thus will lead to lo-

cal elements at the metal surface. If the electrolyte in

front of the electrode is sufﬁciently conductive and does

not allow an ohmic drop, A and B will assume the

same electrode potential Fig. 12.16. In the example of

Fig. 12.16, A will be dissolved at a higher rate than B

and the reduction of hydrogen will occur at a higher

rate on B. Therefore the A sites are the local anodes

and the B sites are the local cathodes. The application

of a polarization π = E − E

R,AB

via an external sup-

ply, such as a potentiostat, allows the determination of

the polarization curve. One measures the current density

i =i

as a function of the polarization π of a metal

surface with local anodes A and cathodes B. Low con-

ductivity of the electrolyte may cause a potential drop

in front of the electrode between sites A and B due to

the local current densities between both. This situation

will be discussed in Sects. 12.2.12 and 12.2.13.

These local elements frequently lead to a pro-

nounced increase of the corrosion rate. A well-known

example is the increase of Zn dissolution by small

deposits of copper at its surface for open-circuit condi-

tions. Hydrogen evolution on the Cu deposits occurs at

i (A/cm

)

E (V)

R,AB

) i

R,AB

)

i = i

+ i

Fig. 12.16 Polarization curve of a metal surface with sites

A and B with different electrochemical properties. Rest po-

tentials E

and E

of pure sites and E

R,AB

of mixed

electrode. Polarization π for the sites A and B and mixed

surface AB. i

, i

are current densities of sites A and B

which compensate each other at E

R,AB

. Inset shows local

elements with current ﬂow from A to B at rest potentials

R,AB

Part D 12.2

684 Part D Materials Performance Testing

Fig. 12.17 Concentration proﬁle in front of an electrode

with Nernst diffusion layer of thickness δ, maximum cur-

rent density i

for c =0

much higher rates, thus promoting zinc dissolution. The

common rest potential is positive when compared to that

of pure zinc. These local elements often cause serious

corrosion damage. Another well-known example is the

corrosion of Cu-containing commercial aluminum. Cu

inclusions prevent the total protection of the Al surface

by a passivating Al

ﬁlm. Cu acts as a local cath-

ode, which compensates the dissolution of Al by local

oxygen reduction. Well-passivated Al does not permit

the reduction of redox systems such as oxygen due

to the isolating electronic properties of the pure pro-

tecting Al

ﬁlm. For similar reasons one should not

combine reactive metals such as Fe with Cu in water-

containing supplies. The close vicinity of both metals

and some Cu dissolution and its redeposition on a re-

active metal surface will cause local elements. Effective

oxygen reduction at these Cu deposits causes increased

Fe dissolution, as described above.

12.2.10 Diffusion Control

of Electrode Processes

In many cases metal corrosion and the compensating

redox process may be under diffusion control, which

leads to a diffusion overvoltage η

. Diffusion of H

ions in weakly acidic electrolytes during Fe dissolution

is one example that was discussed in the last section.

Oxygen diffusion within electrolytes is another. Low

oxygen concentration in solution and thick layers of

electrolyte are a frequent situation that causes diffusion

overvoltage. In all these cases the concentration of the

oxidizing species reduces at the metal surface due to

its intense consumption by the reduction process, lead-

ing to a concentration proﬁle. Similarly high dissolution

Fig. 12.18 i/η dependence for a cathodic reaction un-

der diffusion control without (solid) and with additional

charge-transfer control (dashed line)

rates of a metal cause the accumulation of its cations at

the metal surface and a related increase of its concentra-

tion. As a consequence a concentration proﬁle builds up

which may cause locally saturated or supersaturated so-

lutions and even the precipitation of corrosion products,

such as the formation of salt ﬁlms.

Figure 12.17 presents the concentration proﬁle of

the oxidized component Ox in front of an electrode

within the Nernst diffusion layer of thickness δ. The

dashed line refers to the maximal concentration gradient

when the concentration of Ox at the surface approaches

zero. For a diffusion-controlled electrode process the

transfer of Ox equals the current density i accord-

ing to (12.49) which is a combination of Fick’s ﬁrst

diffusion equation and Faraday’s law with Faraday’s

constant F, the diffusion constant D, the concentra-

tion of Ox at the surface c

and within the bulk c

the thickness of the diffusion layer δ and the number

of electrons for the charge-transfer process n. For van-

ishing concentration c

= 0 one obtains the maximum

diffusion current density i

according to (12.50). The

combination of (12.49)and(12.50) yields (12.51). If

the charge-transfer reaction is fast with respect to diffu-

sion the electrochemical equilibrium is established with

an electrode potential E = E

+η

. η

is given by the

difference of the electrode potentials for the concen-

trations c

and c

according to the Nernst equation,

which yields (12.52). Introducing the current densities

i and i

with (12.49)and(12.50) one obtains (12.53).

Figure 12.19 depicts the change of the current den-

sity with η for a cathodic process which approaches

for large overvoltages. For small η the reaction be-

comes charge-transfer controlled, which results in the

dashed curve of Fig. 12.18. Similarly metal dissolution

for large positive polarizations becomes diffusion con-

Part D 12.2

Corrosion 12.2 Conventional Electrochemical Test Methods 685

Resin

Electrolyte

Resin

Metal

disc

Fig. 12.19

Rotating disc

electrode with

electrolyte con-

vection in front

trolled and the current density becomes independent

of the electrode potential. For large positive overvolt-

ages the accumulation of cations at the electrode surface

yields precipitation of corrosion products and salt ﬁlms

may form, which slow down the metal dissolution rate.

In many cases the growth of oxides ﬁlms at the metal

surface causes a much more pronounced decrease of its

dissolution current density. These processes may lead

to thin passive layers that act as a barrier to the trans-

fer of cations from the metal to the electrolyte, thus

effectively protecting even very reactive metals against

corrosion.

i =−

−c

) nFD

, (12.49)

=−

nFDc

, (12.50)

a) b)

Electrolyte

Metal

Resin

Passive Passive

Fig. 12.20a,b Cross section

of a convex hemispherical

electrode/electrolyte com-

bination (a) and a concave

hemisphere (b) with diffu-

sion lines or current lines

(solid) and curves of equal

concentration or potential

(dashed) respectively; a is

the radius of the electrode

i =i

−

nFDc

, (12.51)





, (12.52)



−i



. (12.53)

Diffusion of oxygen to a corroding metal surface is

frequently the rate-determining step for corrosion pro-

cesses. This is a consequence of its limited dissolution

in water and the presence of thick water layers, which

act as a diffusion barrier. For very thin water layers the

access of oxygen is less hindered and sufﬁciently fast,

yielding high corrosion rates. This is often the case un-

der atmospheric corrosion. As an estimate i

of oxygen

reduction is calculated using the ﬁrst diffusion law ac-

cording to (12.50) with n = 4 for oxygen reduction to

O. With a diffusion constant D

= 10

−5

/sthe

thickness of the Nernst diffusion layer δ = 5×10

−3

and a concentration of saturation for oxygen at

◦

C c

= 2×10

−4

M = 2×10

−7

mol/cm

,avalue

of i

=1.6×10

−4

A/cm

=0.16 mA/cm

is obtained.

This value is relatively large and will also disturb

electrochemical studies in the laboratory as a ca-

thodic background current. It may be suppressed

effectively by purging of electrolytes with nitrogen or

argon.

Diffusion may be enhanced by microelectrodes with

a small radius a. According to Fig. 12.20 the diffusion

in front of a hemispherical electrode follows the cur-

rent lines, which follow the direction of its radius. The

concentration gradient is given by the density of the

hemispheres of constant concentration surrounding the

electrode surface (dashed circles). Most variation is lo-

cated close to the surface due to the divergence of the

current lines. According to the hemispherical shape of

Part D 12.2

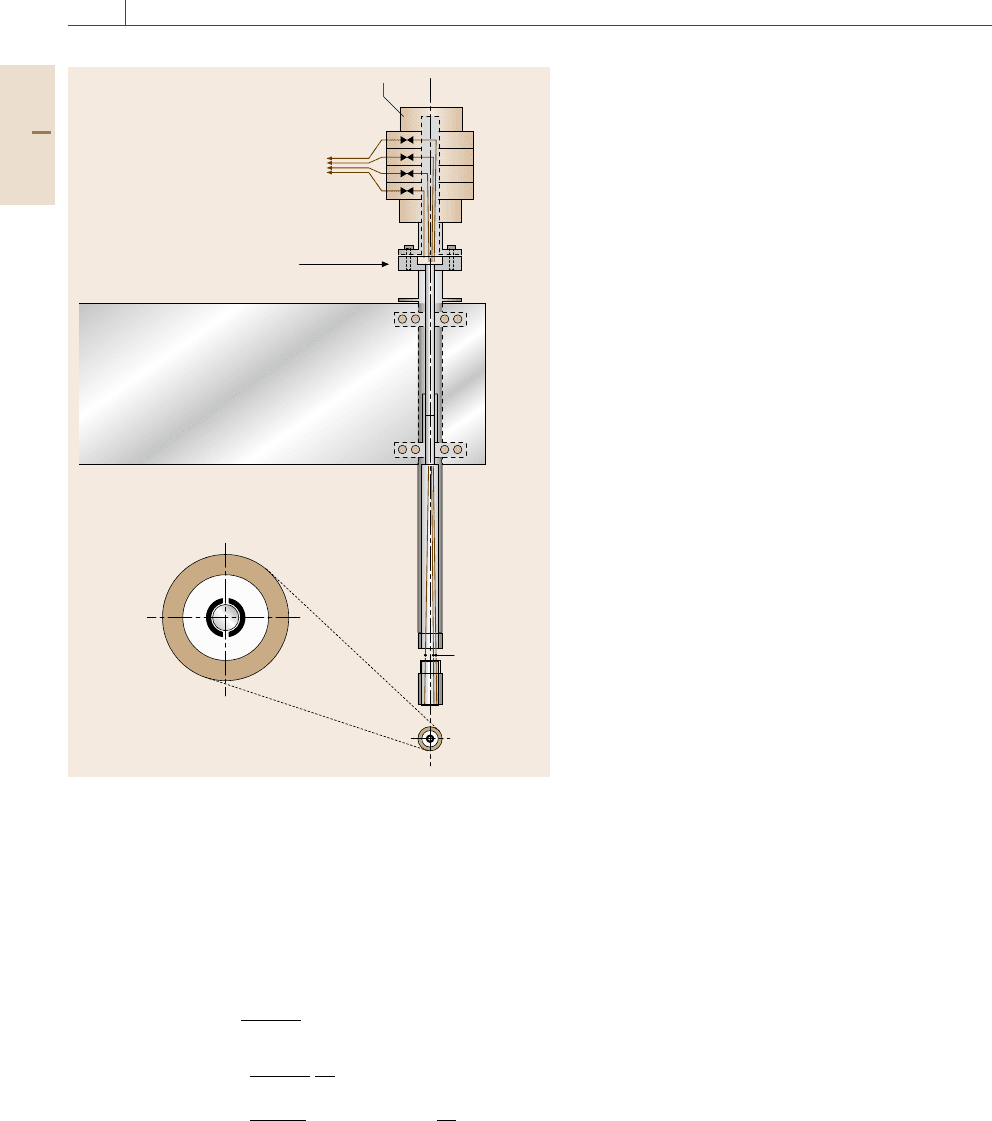
686 Part D Materials Performance Testing

Rotating mercury

contact

Rotator for

split-ring-disc-electrode

Metal disc

Pt-split-ring

Potentiostat

Driving

belt

Contacts

Exchangeable

electrode

Fig. 12.21 Disc rotator with an exchangeable RRDE with a split ring

this transport the current density i(r) decreases with

the distance a +r from the surface according to (12.54)

with the radius a for the metal electrode and the current

density i(a) at its surface. Integration of the ﬁrst diffu-

sion law (12.55) for these conditions in the range r = 0

to r =∞yields (12.56)fori and the limiting current

density i

i(r) =i(a)

(a +r)

, (12.54)

i = nFD

(

a +r

)

, (12.55)

i = nFD

−c

; i

=−nFD

(12.56)

If the radius a becomes small, i

may achieve

large values. For c

= 1M= 10

−3

mol/cm

, n = 1

and D = 5×10

−6

and an ultramicroelectrode

with a radius a = 1 μm = 10

−4

cm one obtains i

5A/cm

. This value will be even higher for elec-

trodes of nm dimensions. In contrast using (12.50)for

a planar electrode with a well-stirred electrolyte and

a diffusion-layer thickness of δ =5×10

−3

cm, one ob-

tains i

= 0.1A/cm

. This is one reason why such

small electrodes are used for electroanalytical purposes.

For similar reasons a small radius leads to small ohmic

voltage drops in front of an ultramicroelectrode which

will be discussed in the next section.

Small active areas on a metal surface of this size

may occur during localized corrosion of a passivated

metal surface. In these cases extremely high local corro-

sion current densities may be measured within corrosion

pits of up to several 10 A/cm

, whereas the rest of the

surface shows extremely small dissolution currents in

the range of μA/cm

. The concentration gradient is

about three times larger in this case due to the con-

cave geometry when compared to a convex hemisphere

(Fig. 12.21b) [12.39]. This more complicated transport

problem has been solved numerically [12.40]. An an-

alytical solution does not exist. Effective hemispherical

transport will delay the accumulation of corrosion prod-

ucts for high dissolution rates, at least for some time

before they precipitate. The precipitation of salt ﬁlms

will decreases the local current density and change

the shape of growing pits from a polygonal shape to

hemispheres due to the electropolishing effect of the

precipitates [12.29,30, 39].

12.2.11 Rotating Disc Electrode (RDE) and

Rotating Ring-Disc Electrode (RRDE)

Diffusion control of electrode processes has been ap-

plied to various polarographic methods to analyze

qualitatively and quantitatively the composition of elec-

trolytes or the products formed at an electrode surface.

The rotating disc electrode (RDE) and rotating ring-disc

electrode (RRDE) are special arrangements to measure

qualitatively and quantitatively the amount and compo-

sition of corrosion products. A disc that rotates with

moderate speed has a laminar ﬂow of the front elec-

trolyte. Its ﬂow is perpendicular and parallel to the

rotating disc, as shown in Fig. 12.19. On one hand

metal dissolution causes an increase of the concen-

tration of the corrosion products during the outward

ﬂow of the electrolyte ﬁlm parallel to the surface. On

the other hand the income of fresh electrolyte from

the bulk perpendicular to the surface yields a de-

crease of the concentration. Both effects compensate

Part D 12.2

Corrosion 12.2 Conventional Electrochemical Test Methods 687

Cell

Control unit

(zero control

amplifier)

Compensation

of ohmic drop

ref 1

ref 2

ref 3

cell 1

cell 2

cell 3

100k

Diff

Adder

100k

Adder

100k

Adder

Fig. 12.22 Tripotentiostat for potentiostatic RRDE studies

each other, so that one may calculate diffusion to the

bulk with a constant thickness of the Nernst diffusion

layer and a constant concentration proﬁle independent

of the location at the disc surface. The quantitative

treatment of this problem yields the Levich equation

(12.57) [12.41] for the thickness of the diffusion layer δ,

with the rotation speed ω =2π f , the frequency f ,

ν =ν



/ρ, i. e. the viscosity ν



divided by the den-

sity ρ of the electrolyte and the diffusion coefﬁcient

D. With ν = 10

−2

/sforwater,D =5×10

−6

and ω = 63 s

−1

one obtains δ = 1.6×10

−3

cm. Intro-

ducing this value in (12.50) yields with n = 1and

=10

−3

M for the limiting disc current density of

a species which is consumed at the disc surface

=300 μA/cm

. Another example is i

ofarotating

iron disc in 0.5MH

. With a saturation concentra-

tion of c = 0.56 M for FeSO

and its bulk concentration

=0 one calculates, for all other conditions the same,

=0.336 A/cm

. Continued Fe dissolution causes ac-

cumulation of corrosion products and leads ﬁnally to

a precipitated salt ﬁlm which restricts the dissolution

to the calculated value. This is close to the experi-

mental maximum i

=200 mA/cm

of dissolution of

a ﬂat iron electrode with moderate agitation of the elec-

trolyte. A better coincidence cannot be expected due to

the difference in hydrodynamic ﬂow between the two

electrodes

δ = 1.61ω

−1/2

1/6

1/3

. (12.57)

The RRDE consist of a central disc with a sur-

rounding analytical ring electrode, usually made of

a noble metal such as gold or platinum (Fig. 12.21).

The products of the central disc are transported par-

allel to the electrode surface and ﬁnally pass the ring

surface where they undergo an electrochemical pro-

cess with a diffusion-limited maximum current density.

The transfer efﬁciency N from the disc to the ring

may be calculated from the dimensions of both elec-

trodes [12.42] or may be determined experimentally.

Val ue s o f N > 30% may be achieved easily. The disc

current I

and the ring current I

are correlated by

(12.58), which takes into account the number of ex-

changed charges n

and n

at both electrodes. With

(12.58) one may calculate I

and the formation of

soluble products at the ring from measured I

values.

A reaction well suited to the experimental calibration

of a RRDE and the determination of N is the re-

dox reaction of [Fe(CN)

]

3−/4−

with an oxidation of

[Fe(CN)

]

4−

at the disc and the related reduction of

Part D 12.2