Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.


518 Г л а в а 15. Комбинаторика. Элементы теории вероятностей
Подставив полученные выражения в формулу (*), находим
P(C) = .
Ответ..
При выполнении упр. 1—6 используйте формулы умноже-
ния и сложения вероятностей.
1. В урне находятся n белых и m черных шаров. Вынимают
два шара. Каова вероятность тоо, что оба шара белые; оба
шара черные?
2. Решите упр. 1 при условии, что вынутые шары возвраща-
ют обратно, а их цвет записывают.
3. Из олоды в 52 арты вынимают 4 арты. Каова вероят-
ность тоо, что все они разных мастей (имеются 4 масти по
13 арт в аждой)?
4. Иральную ость бросают несольо раз. Каова вероят-
ность тоо, что одно очо появится впервые при третьем бро-
сании?
5. На станцию техничесоо обслуживания были доставле-
ны 20 машин. При этом 5 из них имели неисправности в ходо-
вой части, 8 имели неисправности в моторе, а 10 были полно-
стью исправны. Каова вероятность тоо, что машина с неис-
правной ходовой частью имеет таже неисправный мотор?
6. Готовясь вступительному эзамену по математие, аби-
туриент должен подотовить 20 вопросов по элементам матема-
тичесоо анализа и 25 по еометрии. Однао он успел подо-
товить тольо 15 вопросов по элементам математичесоо ана-
лиза и 20 по еометрии. Билет содержит три вопроса, два из
оторых по элементам математичесоо анализа и один по ео-
метрии. Каова вероятность, что: студент сдаст эзамен: а) на
«отлично» (ответит на все три вопроса); б) на «хорошо» (отве-
тит на любые два вопроса)?
Дополнением случайноо события A (или противополож-
ным событием) называют событие C, состоящее в том, что в
результате эсперимента событие A не произошло. Дополне-
ние событию A обозначают . Вероятности событий A и
связаны формулой
P(A) + P() = 1. (8)
Если сложное событие A можно представить в виде
A = A
1
+ A
2
+ ... + A
k
,(9)
2nm
nm+()nm1–+()
----------------------------------------------------
2nm
nm+()nm1–+()
----------------------------------------------------
A A
A
§ 87. Вычисление вероятностей сложных событий 519
де A
i
— события, вероятности оторых известны (i = 1, 2, ..., k),
то вероятность P(A) инода удобно вычислять, используя
формулу
= · · ... · , (10)
связывающую дополнения рассматриваемых событий. Та, в слу-
чае, если A
i
независимы, получаем
P(A) = 1 – P( ) = 1 – P( ) ... P() =
= 1 – [1 – P(A
1
)] ... [1 – P(A
k
)]. (11)
Если все события A
i
равновероятны, то формула (11) примет
более простой вид:
P(A) = 1 – (1 – p)
k
,(12)
де p— вероятность события A
i
.
П р и м е р 2. Для разрушения моста достаточно попадания
одной авиационной бомбы. Найти вероятность разрушения,
если на мост сбрасывают три бомбы с вероятностями попада-
ния 0,3; 0,4; 0,7.
Р е ш е н и е. Найдем вероятность события , состоящео
в том, что мост не будет разрушен. Обозначим через , ,
событие, состоящее в том, что в мост не попала соответственно
первая, вторая и третья бомба. Тода = . Та а из
независимости A
i
следует независимость , то
P() = P()·P()·P( ) = 0,3 · 0,4 · 0,7 = 0,084.
Следовательно, вероятность разрушения моста есть
P(A) = 1 – P( ) = 0,916.
Ответ.0,916.
7. В урне находятся n белых, m черных и k расных шаров.
Наудачу вынимают три шара. Каова вероятность тоо, что хо-
тя бы два шара будут одноо цвета?
8. На стеллаже находятся 15 учебниов, 5 из них в перепле-
те. Наудачу выбирают 3 учебниа. Каова вероятность тоо,
что хотя бы один из них будет в переплета?
9. В лотерее разырывается n билетов, из оторых l выи-
рышных. Нето поупает k билетов. Каова вероятность тоо,
что хотя бы один из упленных билетов выирает?
A
A
1
A
2
A
k
A A
1
A
k
A
A
1
A
2
A
3
A A
1
A
2
A
3
A
i
A A
1
A
2
A
3
A
518 Г л а в а 15. Комбинаторика. Элементы теории вероятностей
Подставив полученные выражения в формулу (*), находим
P(C) = .
Ответ..
При выполнении упр. 1—6 используйте формулы умноже-
ния и сложения вероятностей.
1. В урне находятся n белых и m черных шаров. Вынимают
два шара. Каова вероятность тоо, что оба шара белые; оба
шара черные?
2. Решите упр. 1 при условии, что вынутые шары возвраща-
ют обратно, а их цвет записывают.
3. Из олоды в 52 арты вынимают 4 арты. Каова вероят-
ность тоо, что все они разных мастей (имеются 4 масти по
13 арт в аждой)?
4. Иральную ость бросают несольо раз. Каова вероят-
ность тоо, что одно очо появится впервые при третьем бро-
сании?
5. На станцию техничесоо обслуживания были доставле-
ны 20 машин. При этом 5 из них имели неисправности в ходо-
вой части, 8 имели неисправности в моторе, а 10 были полно-
стью исправны. Каова вероятность тоо, что машина с неис-
правной ходовой частью имеет таже неисправный мотор?
6. Готовясь вступительному эзамену по математие, аби-
туриент должен подотовить 20 вопросов по элементам матема-
тичесоо анализа и 25 по еометрии. Однао он успел подо-
товить тольо 15 вопросов по элементам математичесоо ана-
лиза и 20 по еометрии. Билет содержит три вопроса, два из
оторых по элементам математичесоо анализа и один по ео-
метрии. Каова вероятность, что: студент сдаст эзамен: а) на
«отлично» (ответит на все три вопроса); б) на «хорошо» (отве-
тит на любые два вопроса)?
Дополнением случайноо события A (или противополож-
ным событием) называют событие C, состоящее в том, что в
результате эсперимента событие A не произошло. Дополне-
ние событию A обозначают . Вероятности событий A и
связаны формулой
P(A) + P() = 1. (8)
Если сложное событие A можно представить в виде
A = A
1
+ A
2
+ ... + A
k
,(9)
2nm
nm+()nm1–+()
----------------------------------------------------
2nm
nm+()nm1–+()
----------------------------------------------------
A A
A
§ 87. Вычисление вероятностей сложных событий 519
де A
i
— события, вероятности оторых известны (i = 1, 2, ..., k),
то вероятность P(A) инода удобно вычислять, используя
формулу
= · · ... · , (10)
связывающую дополнения рассматриваемых событий. Та, в слу-
чае, если A
i
независимы, получаем
P(A) = 1 – P( ) = 1 – P( ) ... P() =
= 1 – [1 – P(A
1
)] ... [1 – P(A
k
)]. (11)
Если все события A
i
равновероятны, то формула (11) примет
более простой вид:
P(A) = 1 – (1 – p)
k
,(12)
де p— вероятность события A
i
.
П р и м е р 2. Для разрушения моста достаточно попадания
одной авиационной бомбы. Найти вероятность разрушения,
если на мост сбрасывают три бомбы с вероятностями попада-
ния 0,3; 0,4; 0,7.
Р е ш е н и е. Найдем вероятность события , состоящео
в том, что мост не будет разрушен. Обозначим через , ,
событие, состоящее в том, что в мост не попала соответственно
первая, вторая и третья бомба. Тода = . Та а из
независимости A
i
следует независимость , то
P() = P()·P()·P( ) = 0,3 · 0,4 · 0,7 = 0,084.
Следовательно, вероятность разрушения моста есть
P(A) = 1 – P( ) = 0,916.
Ответ.0,916.
7. В урне находятся n белых, m черных и k расных шаров.
Наудачу вынимают три шара. Каова вероятность тоо, что хо-
тя бы два шара будут одноо цвета?
8. На стеллаже находятся 15 учебниов, 5 из них в перепле-
те. Наудачу выбирают 3 учебниа. Каова вероятность тоо,
что хотя бы один из них будет в переплета?
9. В лотерее разырывается n билетов, из оторых l выи-
рышных. Нето поупает k билетов. Каова вероятность тоо,
что хотя бы один из упленных билетов выирает?
A
A
1
A
2
A
k
A A
1
A
k
A
A
1
A
2
A
3
A A
1
A
2
A
3
A
i
A A
1
A
2
A
3
A

520 Г л а в а 15. Комбинаторика. Элементы теории вероятностей
10. При одном обзоре радиолоационной станцией объет
обнаруживается с вероятностью p. Обнаружение объета в аж-
дом циле происходит независимо от друих цилов. Каова
вероятность тоо, что при n цилах объет будет обнаружен?
11. По неоторой цели производят n выстрелов. Каждый вы-
стрел поражает цель с вероятностью p. Сольо выстрелов надо
произвести, чтобы вероятность поражения цели была не мень-
ше P?
Вероятность события A, оторое может наступить лишь при
появлении одноо из несольих несовместных событий B
1
,
B
2
, ..., B
n
, равна сумме произведений вероятностей аждоо из
этих событий на условную вероятность события A при условии,
что данное событие наступило:
P(A) = P(B
1
)·P(A/B
1
) + P(B
2
) ·P(A/B
2
) + ... + P(B
n
) ·P(A/).
(13)
Равенство (13) называют формлой полной вероятности.
П р и м е р 3. В первой оманде 6 мастеров спорта и 4 пер-
воразрядниа, а во второй — 6 перворазрядниов и 4 мастера
спорта. Сборная, составленная из ироов первой и второй о-
манд, содержит 10 челове: 6 челове из первой оманды и
4 — из второй. Из сборной оманды наудачу выбирают одноо
спортсмена. Каова вероятность тоо, что он мастер спорта?
Р е ш е н и е. Пусть событие B
i
(i = 1, 2) состоит в том, что
наудачу выбранный спортсмен — член i-й оманды. Тода веро-
ятности событий B
i
равны соответственно P(B
1
) = , P(B
2
) = .
Пусть событие A состоит в том, что наудачу выбранный спорт-
смен — мастер спорта. Тода условные вероятности события A
при условии, что выполнено событие B
i
(т. е. известно, из а-
ой оманды спортсмен), равны соответственно P(A/B
1
) = ,
P(A/B
2
) = . Используя формулу полной вероятности, получаем
P(A) = · + · = .
Ответ..
B
n
3
5
---
2
5
---
3
5
---
2
5
---
3
5
---
3
5
---
2
5
---
2
5
---
13
25
------
13
25
------
§ 87. Вычисление вероятностей сложных событий 521
12. Эзамен происходит по следующей схеме: если неото-
рый билет уже был вытянут, то эзаменатор отладывает ео,
т. е. последующие эзаменующиеся не моут вытянуть этот би-
лет. Учени выучил k билетов (k < n). В аом случае вероят-
ность тоо, что учени вытянет выученный билет, больше —
ода он идет отвечать первым или последним?
13. В урне находятся два шара, цвета оторых неизвестны
(аждый шар может быть или белым, или черным). В урну по-
ложили белый шар. Каова станет вероятность вынуть из урны
белый шар?
14. Имеются 5 винтово, из оторых 3 снайперсие и 2 обыч-
ные. Наудачу выбирают одну винтову и из нее производят вы-
стрел. Найдите вероятность попадания, если вероятности попа-
дания из снайперсой и обычной винтови равны соответствен-
но 0,95 и 0,7.
15. Имеются две урны. В первой находятся m белых и n чер-
ных шаров, а во второй — k белых и l черных шаров. Из первой
урны во вторую переложили один шар. Каова вероятность
после этоо вынуть:
а) белый шар из первой урны;
б) белый шар из второй урны?
16. Имеются две партии однородных изделий с разным со-
ставом стандартных и дефетных: в первой партии всео N из-
делий, из них n дефетных, во второй партии M изделий, из
них m дефетных. Из первой партии берут K изделий, из вто-
рой L изделий и образуют новую партию. Каова вероятность
тоо, что изделие, выбранное наудачу из новой партии, оа-
жется дефетным?
17. В условиях упр. 16 найдите вероятность тоо, что среди
трех выбранных наудачу из вновь образованной партии изде-
лий хотя бы одно оажется дефетным.

520 Г л а в а 15. Комбинаторика. Элементы теории вероятностей
10. При одном обзоре радиолоационной станцией объет
обнаруживается с вероятностью p. Обнаружение объета в аж-
дом циле происходит независимо от друих цилов. Каова
вероятность тоо, что при n цилах объет будет обнаружен?
11. По неоторой цели производят n выстрелов. Каждый вы-
стрел поражает цель с вероятностью p. Сольо выстрелов надо
произвести, чтобы вероятность поражения цели была не мень-
ше P?
Вероятность события A, оторое может наступить лишь при
появлении одноо из несольих несовместных событий B
1
,
B
2
, ..., B
n
, равна сумме произведений вероятностей аждоо из
этих событий на условную вероятность события A при условии,
что данное событие наступило:
P(A) = P(B
1
)·P(A/B
1
) + P(B
2
) ·P(A/B
2
) + ... + P(B
n
) ·P(A/).
(13)
Равенство (13) называют формлой полной вероятности.
П р и м е р 3. В первой оманде 6 мастеров спорта и 4 пер-
воразрядниа, а во второй — 6 перворазрядниов и 4 мастера
спорта. Сборная, составленная из ироов первой и второй о-
манд, содержит 10 челове: 6 челове из первой оманды и
4 — из второй. Из сборной оманды наудачу выбирают одноо
спортсмена. Каова вероятность тоо, что он мастер спорта?
Р е ш е н и е. Пусть событие B
i
(i = 1, 2) состоит в том, что
наудачу выбранный спортсмен — член i-й оманды. Тода веро-
ятности событий B
i
равны соответственно P(B
1
) = , P(B
2
) = .
Пусть событие A состоит в том, что наудачу выбранный спорт-
смен — мастер спорта. Тода условные вероятности события A
при условии, что выполнено событие B
i
(т. е. известно, из а-
ой оманды спортсмен), равны соответственно P(A/B
1
) = ,
P(A/B
2
) = . Используя формулу полной вероятности, получаем
P(A) = · + · = .
Ответ..
B
n
3
5
---
2
5
---
3
5
---
2
5
---
3
5
---
3
5
---
2
5
---
2
5
---
13
25
------
13
25
------
§ 87. Вычисление вероятностей сложных событий 521
12. Эзамен происходит по следующей схеме: если неото-
рый билет уже был вытянут, то эзаменатор отладывает ео,
т. е. последующие эзаменующиеся не моут вытянуть этот би-
лет. Учени выучил k билетов (k < n). В аом случае вероят-
ность тоо, что учени вытянет выученный билет, больше —
ода он идет отвечать первым или последним?
13. В урне находятся два шара, цвета оторых неизвестны
(аждый шар может быть или белым, или черным). В урну по-
ложили белый шар. Каова станет вероятность вынуть из урны
белый шар?
14. Имеются 5 винтово, из оторых 3 снайперсие и 2 обыч-
ные. Наудачу выбирают одну винтову и из нее производят вы-
стрел. Найдите вероятность попадания, если вероятности попа-
дания из снайперсой и обычной винтови равны соответствен-
но 0,95 и 0,7.
15. Имеются две урны. В первой находятся m белых и n чер-
ных шаров, а во второй — k белых и l черных шаров. Из первой
урны во вторую переложили один шар. Каова вероятность
после этоо вынуть:
а) белый шар из первой урны;
б) белый шар из второй урны?
16. Имеются две партии однородных изделий с разным со-
ставом стандартных и дефетных: в первой партии всео N из-
делий, из них n дефетных, во второй партии M изделий, из
них m дефетных. Из первой партии берут K изделий, из вто-
рой L изделий и образуют новую партию. Каова вероятность
тоо, что изделие, выбранное наудачу из новой партии, оа-
жется дефетным?
17. В условиях упр. 16 найдите вероятность тоо, что среди
трех выбранных наудачу из вновь образованной партии изде-
лий хотя бы одно оажется дефетным.

Глава 16
Элементы математической логики.
Системы счисления
§ 88. Высказывания
Под высазыванием понимают утверждение, о отором
имеет смысл оворить, истинно оно или ложно.
Из заданных высазываний с помощью та называемых ло-
ичесих связо, оторым в обычной речи соответствуют час-
тица «не», союзы «и», «или», сложноподчиненный оборот
«если..., то...», выражение «в том и тольо в том случае», обра-
зуют новые составные высазывания. Если истинному выса-
зыванию поставить в соответствие 1, а ложному 0, то лоиче-
сие связи можно формально определить с помощью та на-
зываемых таблиц истинности.
Основные понятия, связанные с высазываниями.
1. Отрицание (читают: «не p» и пишут ). Кода p истин-
но, тода ложно, и наоборот.
2. Конъюнция (или лоичесое множение) двух выса-
зываний (читают: «p и q» и пишут p , q). Конъюнция истинна
тольо в том случае, ода оба высазывания истинны.
3. Дизъюнция (или лоичесое сложение) двух высазы-
ваний (читают: «p или q» и пишут p # q). Дизъюнция истинна
в том случае, ода истинно хотя бы одно из двух высазываний.
4. Имплиация (читают: «если p, то q» и пишут p º q).
Здесь два высазывания в отличие от случаев 2 и 3 не переста-
новочны: высазывание p называют словием, а высазывание
q— следствием. Имплиация ложна тольо в том случае,
ода условие истинно, а следствие ложно.
5. Эвиваленция (или двойная имплиация) (читают: «p
эвивалентно q» и пишут p J q). Эвиваленция истинна в том
случае, ода или оба высазывания истинны, или оба выса-
зывания ложны.
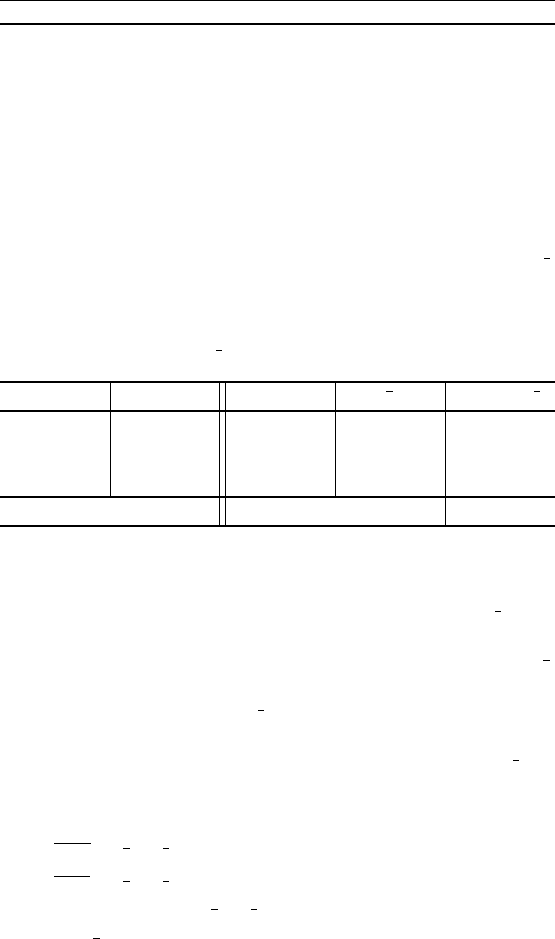
Таблица истинности элементарных высазываний имеет вид
pqp # qp , qp º q
00 0011
01 1011
10 1000
11 1110
p
p
p
§ 88. Высказывания 523
Новые высазывания образуют, используя лоичесие опе-
рации. Таие операции можно применять мнооратно. Поря-
до, в отором производятся операции, уазывают с помощью
собо.
Если из p следует q и из q следует p, то высазывания p и q
называют равносильными. Равносильные высазывания со-
единяют знаом _ либо знаом равенства.
Таблицы истинности для равносильных высазываний сов-
падают.
П р и м е р 1. Доазать, что высазывания p º q и (p , q) #
равносильны.
Р е ш е н и е. Таблица истинности для высазывания p º q
была представлена выше. Составим таблицу истинности для
высазывания (p , q) # :
В последней строе таблицы римсими цифрами обозначим
номера шаов, в результате оторых составляем таблицу ис-
тинности. На I шае заполняем столбцы истинности для выса-
зываний p и q, на II шае — для высазываний p , q и . При
этом используем таблицу истинности элементарных высазы-
ваний, приведенную выше. На III шае, рассматривая p , q и
а простейшие высазывания, заполним столбец дизъюнции
этих высазываний (p , q) # . Полученный столбец истиннос-
ти совпадает со столбцом истинности высазывания p º q.
Ита, равносильность высазываний p º q и (p , q) # ус-
тановлена.
Сравнив таблицы истинности, доажите:
1. = , .
2. = # .
3. p J q = (p , q) # ( , ).
4. (p # ) , q = q.
5. p # (p , q) = p.
pqp , q (p , q) #
00 011
01 011
10 000
11 101
I II III
p
p
p p
p
p
p
p
p # q p q
p , q p q
p q
q
Глава 16
Элементы математической логики.
Системы счисления
§ 88. Высказывания
Под высазыванием понимают утверждение, о отором
имеет смысл оворить, истинно оно или ложно.
Из заданных высазываний с помощью та называемых ло-
ичесих связо, оторым в обычной речи соответствуют час-
тица «не», союзы «и», «или», сложноподчиненный оборот
«если..., то...», выражение «в том и тольо в том случае», обра-
зуют новые составные высазывания. Если истинному выса-
зыванию поставить в соответствие 1, а ложному 0, то лоиче-
сие связи можно формально определить с помощью та на-
зываемых таблиц истинности.
Основные понятия, связанные с высазываниями.
1. Отрицание (читают: «не p» и пишут ). Кода p истин-
но, тода ложно, и наоборот.
2. Конъюнция (или лоичесое множение) двух выса-
зываний (читают: «p и q» и пишут p , q). Конъюнция истинна
тольо в том случае, ода оба высазывания истинны.
3. Дизъюнция (или лоичесое сложение) двух высазы-
ваний (читают: «p или q» и пишут p # q). Дизъюнция истинна
в том случае, ода истинно хотя бы одно из двух высазываний.
4. Имплиация (читают: «если p, то q» и пишут p º q).
Здесь два высазывания в отличие от случаев 2 и 3 не переста-
новочны: высазывание p называют словием, а высазывание
q— следствием. Имплиация ложна тольо в том случае,
ода условие истинно, а следствие ложно.
5. Эвиваленция (или двойная имплиация) (читают: «p
эвивалентно q» и пишут p J q). Эвиваленция истинна в том
случае, ода или оба высазывания истинны, или оба выса-
зывания ложны.
Таблица истинности элементарных высазываний имеет вид
pqp # qp , qp º q
00 0011
01 1011
10 1000
11 1110
p
p
p
§ 88. Высказывания 523
Новые высазывания образуют, используя лоичесие опе-
рации. Таие операции можно применять мнооратно. Поря-
до, в отором производятся операции, уазывают с помощью
собо.
Если из p следует q и из q следует p, то высазывания p и q
называют равносильными. Равносильные высазывания со-
единяют знаом _ либо знаом равенства.
Таблицы истинности для равносильных высазываний сов-
падают.
П р и м е р 1. Доазать, что высазывания p º q и (p , q) #
равносильны.
Р е ш е н и е. Таблица истинности для высазывания p º q
была представлена выше. Составим таблицу истинности для
высазывания (p , q) # :
В последней строе таблицы римсими цифрами обозначим
номера шаов, в результате оторых составляем таблицу ис-
тинности. На I шае заполняем столбцы истинности для выса-
зываний p и q, на II шае — для высазываний p , q и . При
этом используем таблицу истинности элементарных высазы-
ваний, приведенную выше. На III шае, рассматривая p , q и
а простейшие высазывания, заполним столбец дизъюнции
этих высазываний (p , q) # . Полученный столбец истиннос-
ти совпадает со столбцом истинности высазывания p º q.
Ита, равносильность высазываний p º q и (p , q) # ус-
тановлена.
Сравнив таблицы истинности, доажите:
1. = , .
2. = # .
3. p J q = (p , q) # ( , ).
4. (p # ) , q = q.
5. p # (p , q) = p.
pqp , q (p , q) #
00 011
01 011
10 000
11 101
I II III
p
p
p p
p
p
p
p
p # q p q
p , q p q
p q
q

524 Г л а в а 16. Элементы матем. логики. Системы счисления
16. Высазывание p означает, что у вас есть собаа, а выса-
зывание q— что у вас есть оша. Сформулируйте, что означа-
ет заданное составное высазывание:
1а) # q;б) , ; в)(p , q) # ( , ); ) º q.
17. Пусть высазывание p | q означает, что p и q не моут
быть оба истинными. Составьте таблицу истинности для p | q.
18. Запишите высазывание p | q (см. упр. 7), используя ло-
ичесие связи онъюнции, дизъюнции и отрицания.
19. Доажите равносильность высазываний (p | ) | (p | q)
и p , q.
10. Пусть p означает «идет дождь», а q означает «дует ве-
тер». Запишите в символичесой форме высазывание:
а) «если идет дождь, то дует ветер»;
б) «если дует ветер, то идет дождь»;
в) «ветер дует в том и тольо в том случае, ода идет
дождь»;
) «если дует ветер, то нет дождя»;
д) «неверно, что ветер дует тода и тольо тода, ода нет
дождя».
11. Запишите в символичесой форме сложное высазыва-
ние, состоящее из простых высазываний p, q, r, истинное то-
да и тольо тода, ода истинна тольо одна (безразлично а-
ая) из омпонент.
12. По мишени произведены три выстрела. Пусть p
i
означа-
ет высазывание: «мишень поражена при i-м выстреле». Сфор-
мулируйте, что означает следующее высазывание, записанное
в символичесой форме:
а) p
1
# p
2
# p
3
;б)p
1
, p
2
, p
3
;в)(
1
#
2
) , p
3
.
Лео проверить равносильность следующих высазываний
(здесь I — истина, L — ложь):
p # q = q # p,(1)
p , q = q , p,(2)
p # (q # r) = (p # q) # r, (3)
p , (q , r) = (p , q) , r,(4)
p , (q # r) = (p , q) # (p , r), (5)
p , p = p, (6)
p # p = p,(7)
p # = I,(8)
p
p q p q p
q
p p
p
§ 88. Высказывания 525
p , = L,(9)
p , I = p,(10)
p # I = I,(11)
p , L = L,(12)
p # L = p.(13)
Используя формулы (1)—(13), можно решать довольно слож-
ные лоичесие задачи.
П р и м е р 2. Витор, Роман, Юрий и Серей заняли на ма-
тематичесой олимпиаде первые четыре места. Кода их спро-
сили о распределении мест, они дали три таих ответа:
1) Серей — первый, Роман — второй;
2) Серей — второй, Витор — третий;
3) Юрий — второй, Витор — четвертый.
Ка распределились места, если в аждом ответе тольо од-
но утверждение истинно?
Р е ш е н и е. Та а в аждом ответе одно из утверждений
истинно, то и дизъюнция этих утверждений таже истинна.
Например, истинно высазывание: «или Серей первый, или
Роман — второй». Запишем это высазывание в следующем
символичесом виде: С
I
# Р
II
. Аналоично, высазывания ос-
тальных ответов имеют вид С
II
# В
III
и Ю
II
# В
IV
соответствен-
но. Конъюнция истинных высазываний истинна. Следова-
тельно, истинным является составное высазывание
(С
I
# Р
II
) , (С
II
# В
III
) , (Ю
II
# В
IV
). (*)
Используя формулы (1)—(13), упростим высазывание (*).
Для этоо представим в виде дизъюнции простейших онъ-
юнций первую онъюнцию:
(С
I
# Р
II
) , (С
II
# В
III
) = [(С
I
# Р
II
) , С
II
] # [(С
I
# Р
II
) , В
III
] =
= [(С
I
, С
II
) # (Р
II
, С
II
)] # [(С
I
, В
III
) # (Р
II
, В
III
)]. (**)
Высазывание, записанное в первых вадратных собах пра-
вой части равенства (**), ложно, посольу является дизъюн-
цией двух ложных высазываний С
I
, С
II
и Р
II
, С
II
: первое из
них состоит в том, что Серей занял одновременно первое и вто-
рое места, а второе — в том, что второе место одновременно за-
няли Роман и Серей. Таим образом, первая онъюнция
примет вид
(С
I
# Р
II
) , (С
II
# В
III
) = (С
I
, В
III
) # (Р
II
, В
III
).
p

524 Г л а в а 16. Элементы матем. логики. Системы счисления
16. Высазывание p означает, что у вас есть собаа, а выса-
зывание q— что у вас есть оша. Сформулируйте, что означа-
ет заданное составное высазывание:
1а) # q;б) , ; в)(p , q) # ( , ); ) º q.
17. Пусть высазывание p | q означает, что p и q не моут
быть оба истинными. Составьте таблицу истинности для p | q.
18. Запишите высазывание p | q (см. упр. 7), используя ло-
ичесие связи онъюнции, дизъюнции и отрицания.
19. Доажите равносильность высазываний (p | ) | (p | q)
и p , q.
10. Пусть p означает «идет дождь», а q означает «дует ве-
тер». Запишите в символичесой форме высазывание:
а) «если идет дождь, то дует ветер»;
б) «если дует ветер, то идет дождь»;
в) «ветер дует в том и тольо в том случае, ода идет
дождь»;
) «если дует ветер, то нет дождя»;
д) «неверно, что ветер дует тода и тольо тода, ода нет
дождя».
11. Запишите в символичесой форме сложное высазыва-
ние, состоящее из простых высазываний p, q, r, истинное то-
да и тольо тода, ода истинна тольо одна (безразлично а-
ая) из омпонент.
12. По мишени произведены три выстрела. Пусть p
i
означа-
ет высазывание: «мишень поражена при i-м выстреле». Сфор-
мулируйте, что означает следующее высазывание, записанное
в символичесой форме:
а) p
1
# p
2
# p
3
;б)p
1
, p
2
, p
3
;в)(
1
#
2
) , p
3
.
Лео проверить равносильность следующих высазываний
(здесь I — истина, L — ложь):
p # q = q # p,(1)
p , q = q , p,(2)
p # (q # r) = (p # q) # r, (3)
p , (q , r) = (p , q) , r,(4)
p , (q # r) = (p , q) # (p , r), (5)
p , p = p, (6)
p # p = p,(7)
p # = I,(8)
p
p q p q p
q
p p
p
§ 88. Высказывания 525
p , = L,(9)
p , I = p,(10)
p # I = I,(11)
p , L = L,(12)
p # L = p.(13)
Используя формулы (1)—(13), можно решать довольно слож-
ные лоичесие задачи.
П р и м е р 2. Витор, Роман, Юрий и Серей заняли на ма-
тематичесой олимпиаде первые четыре места. Кода их спро-
сили о распределении мест, они дали три таих ответа:
1) Серей — первый, Роман — второй;
2) Серей — второй, Витор — третий;
3) Юрий — второй, Витор — четвертый.
Ка распределились места, если в аждом ответе тольо од-
но утверждение истинно?
Р е ш е н и е. Та а в аждом ответе одно из утверждений
истинно, то и дизъюнция этих утверждений таже истинна.
Например, истинно высазывание: «или Серей первый, или
Роман — второй». Запишем это высазывание в следующем
символичесом виде: С
I
# Р
II
. Аналоично, высазывания ос-
тальных ответов имеют вид С
II
# В
III
и Ю
II
# В
IV
соответствен-
но. Конъюнция истинных высазываний истинна. Следова-
тельно, истинным является составное высазывание
(С
I
# Р
II
) , (С
II
# В
III
) , (Ю
II
# В
IV
). (*)
Используя формулы (1)—(13), упростим высазывание (*).
Для этоо представим в виде дизъюнции простейших онъ-
юнций первую онъюнцию:
(С
I
# Р
II
) , (С
II
# В
III
) = [(С
I
# Р
II
) , С
II
] # [(С
I
# Р
II
) , В
III
] =
= [(С
I
, С
II
) # (Р
II
, С
II
)] # [(С
I
, В
III
) # (Р
II
, В
III
)]. (**)
Высазывание, записанное в первых вадратных собах пра-
вой части равенства (**), ложно, посольу является дизъюн-
цией двух ложных высазываний С
I
, С
II
и Р
II
, С
II
: первое из
них состоит в том, что Серей занял одновременно первое и вто-
рое места, а второе — в том, что второе место одновременно за-
няли Роман и Серей. Таим образом, первая онъюнция
примет вид
(С
I
# Р
II
) , (С
II
# В
III
) = (С
I
, В
III
) # (Р
II
, В
III
).
p

526 Г л а в а 16. Элементы матем. логики. Системы счисления
Тода онъюнция (**) запишется та:
[(С
I
, В
III
) # (Р
II
, В
III
)] , (Ю
II
# В
IV
).
Используя по-прежнему формулы (1)—(13), имеем
{[(С
I
, В
III
) # (Р
II
, В
III
)] , Ю
II
} #
# {[(С
I
, В
III
) # (Р
II
, В
III
)] , В
IV
} =
= (С
I
, В
III
, Ю
II
) # (Р
II
, В
III
, Ю
II
) # (С
I
, В
III
, В
IV
) #
# (Р
II
, В
III
, В
IV
) = (С
I
, В
III
, Ю
II
).
Действительно, второе, третье и четвертое высазывания,
участвующие в этой дизъюнции, ложны, та а являются
онъюнциями или одинаовых був с разными номерами, или
разных був с одинаовыми номерами, чео быть не может.
Ита, истинной является онъюнция С
I
, В
III
, Ю
II
.
Ответ. Первое место занял Серей, второе — Юрий, третье —
Витор и четвертое — Роман.
13. По обвинению в ораблении перед судом предстали A, B, C.
Установлено следующее:
а) если A не виновен или B виновен, то C виновен;
б) если A не виновен, то C не виновен.
Виновен ли A?
14. Определите, то из четырех подозреваемых участвовал
в ораблении, по следующим данным:
а) если A участвовал, то и B участвовал;
б) если
B
участвовал, то или
C
участвовал, или
A
не участ-
вовал;
в) если D не участвовал, то A участвовал, а C не участвовал;
) если D участвовал, то A участвовал.
15. Эзамен сдавали три студента A, B и C. Известно, что:
а) если A не сдал или B сдал, то C сдал;
б) если A не сдал, то C не сдал.
Можно ли на основании этих данных установить, то сдал
эзамен?
В начале парарафа было поазано, а построить таблицу
истинности любоо составноо высазывания. Представляет ин-
терес и обратная задача: по заданной таблице истинности най-
ти одно или несольо высазываний, оторым оно соответст-
вует. Оазывается, обратная задача не тольо имеет решение,
но ео можно получить, используя лишь следующие лоичесие
связи: ,, #, .
§ 88. Высказывания 527
П р и м е р 3. Найти высазывание, состоящее из двух про-
стейших высазываний p и q, имеющее следующую таблицу
истинности (см. таблицу слева):
Р е ш е н и е. Единица в последнем столбце таблицы при-
сутствует тольо в последней строе. Следовательно, можно
предположить, что истинным является высазывание , .
Проверим это утверждение. Для этоо составим таблицу истин-
ности высазывания , (см. таблицу справа). Действитель-
но, полученная таблица совпадает с исходной. Ита, найденное
высазывание истинное.
16. Постройте три составных высазывания a, b, c, имею-
щих следующие таблицы истинности:
17. Каие высазывания a, b, c, d имеют следующие табли-
цы истинности:
pq ? ,
10 0 01 0
11 0 00 0
01 0 10 0
00 1 11 1
pqr abc
111 101
110 001
101 101
100 010
011 001
010 101
001 000
000 001
pq abcd
11 1100
10 0001
01 0010
00 1000
p q p q
p q
p q
526 Г л а в а 16. Элементы матем. логики. Системы счисления
Тода онъюнция (**) запишется та:
[(С
I
, В
III
) # (Р
II
, В
III
)] , (Ю
II
# В
IV
).
Используя по-прежнему формулы (1)—(13), имеем
{[(С
I
, В
III
) # (Р
II
, В
III
)] , Ю
II
} #
# {[(С
I
, В
III
) # (Р
II
, В
III
)] , В
IV
} =
= (С
I
, В
III
, Ю
II
) # (Р
II
, В
III
, Ю
II
) # (С
I
, В
III
, В
IV
) #
# (Р
II
, В
III
, В
IV
) = (С
I
, В
III
, Ю
II
).
Действительно, второе, третье и четвертое высазывания,
участвующие в этой дизъюнции, ложны, та а являются
онъюнциями или одинаовых був с разными номерами, или
разных був с одинаовыми номерами, чео быть не может.
Ита, истинной является онъюнция С
I
, В
III
, Ю
II
.
Ответ. Первое место занял Серей, второе — Юрий, третье —
Витор и четвертое — Роман.
13. По обвинению в ораблении перед судом предстали A, B, C.
Установлено следующее:
а) если A не виновен или B виновен, то C виновен;
б) если A не виновен, то C не виновен.
Виновен ли A?
14. Определите, то из четырех подозреваемых участвовал
в ораблении, по следующим данным:
а) если A участвовал, то и B участвовал;
б) если
B
участвовал, то или
C
участвовал, или
A
не участ-
вовал;
в) если D не участвовал, то A участвовал, а C не участвовал;
) если D участвовал, то A участвовал.
15. Эзамен сдавали три студента A, B и C. Известно, что:
а) если A не сдал или B сдал, то C сдал;
б) если A не сдал, то C не сдал.
Можно ли на основании этих данных установить, то сдал
эзамен?
В начале парарафа было поазано, а построить таблицу
истинности любоо составноо высазывания. Представляет ин-
терес и обратная задача: по заданной таблице истинности най-
ти одно или несольо высазываний, оторым оно соответст-
вует. Оазывается, обратная задача не тольо имеет решение,
но ео можно получить, используя лишь следующие лоичесие
связи: ,, #, .
§ 88. Высказывания 527
П р и м е р 3. Найти высазывание, состоящее из двух про-
стейших высазываний p и q, имеющее следующую таблицу
истинности (см. таблицу слева):
Р е ш е н и е. Единица в последнем столбце таблицы при-
сутствует тольо в последней строе. Следовательно, можно
предположить, что истинным является высазывание , .
Проверим это утверждение. Для этоо составим таблицу истин-
ности высазывания , (см. таблицу справа). Действитель-
но, полученная таблица совпадает с исходной. Ита, найденное
высазывание истинное.
16. Постройте три составных высазывания a, b, c, имею-
щих следующие таблицы истинности:
17. Каие высазывания a, b, c, d имеют следующие табли-
цы истинности:
pq ? ,
10 0 01 0
11 0 00 0
01 0 10 0
00 1 11 1
pqr abc
111 101
110 001
101 101
100 010
011 001
010 101
001 000
000 001
pq abcd
11 1100
10 0001
01 0010
00 1000
p q p q
p q
p q
