Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.


528 Г л а в а 16. Элементы матем. логики. Системы счисления
Ка следует из примера 3, а таже из решений упр. 16 и 17,
алоритм построения составноо высазывания залючается в
дизъюнции тех онъюнций простых высазываний, ото-
рым соответствует единица в последнем столбце таблицы ис-
тинности. При этом в отдельную онъюнцию входит либо вы-
сазывание, либо ео отрицание в зависимости от тоо, соответ-
ствуют ли ему в таблице единица или нуль.
Попробуем использовать этот метод в следующей «жизнен-
ной» ситуации.
Пример 4. Имеются орода A и B. В ороде A живут лю-
ди, вседа оворящие правду, а в ороде B живут лжецы, вседа
оворящие неправду. Жители обоих ородов свободно ходят
в ости дру друу, поэтому в аждом ороде можно встретить
жителей любоо из них. Каой вопрос должен задать путешест-
венни первому встречному, чтобы по единственному ответу
(«да» или «нет») выяснить, в аом ороде он находится?
Решение. Пусть p означает высазывание «вы оворите
правду», а q— высазывание «это ород A». Требуется задать
единственный вопрос, на оторый ответ «да» означал бы, что q
истинно, а ответ «нет» — что q ложно, независимо от правди-
вости первоо встречноо.
Если челове оворит правду, то он сажет «да», если вы-
сазывание истинно, и «нет» — если оно ложно; лжец посту-
пит наоборот. Таблица истинности высазывания (ожидаемоо
ответа) имеет следующий вид:
Эта таблица истинности соответствует эвивалентности,
т. е. (p J q), или высазыванию
(p , q) # ( , ).
Таим образом, заданный первому встречному вопрос дол-
жен установить, является ли истинной эвивалентность места
жительства спрашиваемоо человеа и ео правдивость:«Верно
pqОжидаемый ответ
11да1
10нет0
01да0
00нет1
p q
§ 88. Высказывания 529
ли, что это ород A и вы ео житель, или это ород B и вы ео
житель?» С помощью этоо вопроса нужно выяснить, живет ли
этот челове в данном ороде, поэтому ео можно сформулиро-
вать ороче: «Вы житель этоо орода?»
18. Один лои попал диарям и был залючен в темни-
цу, имеющую два выхода. Вождь диарей предложил пленни-
у следующий шанс на спасение: «Один выход ведет на верную
смерть, друой — на свободу. Ты можешь избрать любой. Сде-
лать выбор тебе помоут два моих воина. Они останутся здесь,
чтобы ответить на один твой вопрос — любой, аой ты поже-
лаешь им задать. Но я предупреждаю тебя, что один воин все-
да оворит правду, а второй вседа лжет». И вождь ушел. Через
неоторое время лои, задав вопрос одному из воинов, вышел
на свободу. Каой вопрос он задал?
П р и м е р 5. Староста, физор и профор хотят использо-
вать элетричесую схему, реистрирующую результаты тай-
ноо олосования большинством олосов. Ка она должна вы-
лядеть?
Решение. Пусть p— высазывание «староста олосует
за», q— высазывание «физор олосует за», r — высазыва-
ние «профор олосует за». Составим таблицу истинности инте-
ресующео нас высазывания:
Единицы в последнем столбце поставлены в тех строах,
де число единиц больше числа нулей.
Исомое высазывание имеет вид
(p , q , r) # (p , q , ) # (p , , r) # ( , q , r).
pqrИсомое высазывание
111 1p , q , r
110 1p , q ,
101 1p , , r
011 1 , q , r
100 0
010 0
001 0
000 0
r
q
p
r q p

528 Г л а в а 16. Элементы матем. логики. Системы счисления
Ка следует из примера 3, а таже из решений упр. 16 и 17,
алоритм построения составноо высазывания залючается в
дизъюнции тех онъюнций простых высазываний, ото-
рым соответствует единица в последнем столбце таблицы ис-
тинности. При этом в отдельную онъюнцию входит либо вы-
сазывание, либо ео отрицание в зависимости от тоо, соответ-
ствуют ли ему в таблице единица или нуль.
Попробуем использовать этот метод в следующей «жизнен-
ной» ситуации.
Пример 4. Имеются орода A и B. В ороде A живут лю-
ди, вседа оворящие правду, а в ороде B живут лжецы, вседа
оворящие неправду. Жители обоих ородов свободно ходят
в ости дру друу, поэтому в аждом ороде можно встретить
жителей любоо из них. Каой вопрос должен задать путешест-
венни первому встречному, чтобы по единственному ответу
(«да» или «нет») выяснить, в аом ороде он находится?
Решение. Пусть p означает высазывание «вы оворите
правду», а q— высазывание «это ород A». Требуется задать
единственный вопрос, на оторый ответ «да» означал бы, что q
истинно, а ответ «нет» — что q ложно, независимо от правди-
вости первоо встречноо.
Если челове оворит правду, то он сажет «да», если вы-
сазывание истинно, и «нет» — если оно ложно; лжец посту-
пит наоборот. Таблица истинности высазывания (ожидаемоо
ответа) имеет следующий вид:
Эта таблица истинности соответствует эвивалентности,
т. е. (p J q), или высазыванию
(p , q) # ( , ).
Таим образом, заданный первому встречному вопрос дол-
жен установить, является ли истинной эвивалентность места
жительства спрашиваемоо человеа и ео правдивость:«Верно
pqОжидаемый ответ
11да1
10нет0
01да0
00нет1
p q
§ 88. Высказывания 529
ли, что это ород A и вы ео житель, или это ород B и вы ео
житель?» С помощью этоо вопроса нужно выяснить, живет ли
этот челове в данном ороде, поэтому ео можно сформулиро-
вать ороче: «Вы житель этоо орода?»
18. Один лои попал диарям и был залючен в темни-
цу, имеющую два выхода. Вождь диарей предложил пленни-
у следующий шанс на спасение: «Один выход ведет на верную
смерть, друой — на свободу. Ты можешь избрать любой. Сде-
лать выбор тебе помоут два моих воина. Они останутся здесь,
чтобы ответить на один твой вопрос — любой, аой ты поже-
лаешь им задать. Но я предупреждаю тебя, что один воин все-
да оворит правду, а второй вседа лжет». И вождь ушел. Через
неоторое время лои, задав вопрос одному из воинов, вышел
на свободу. Каой вопрос он задал?
П р и м е р 5. Староста, физор и профор хотят использо-
вать элетричесую схему, реистрирующую результаты тай-
ноо олосования большинством олосов. Ка она должна вы-
лядеть?
Решение. Пусть p— высазывание «староста олосует
за», q— высазывание «физор олосует за», r — высазыва-
ние «профор олосует за». Составим таблицу истинности инте-
ресующео нас высазывания:
Единицы в последнем столбце поставлены в тех строах,
де число единиц больше числа нулей.
Исомое высазывание имеет вид
(p , q , r) # (p , q , ) # (p , , r) # ( , q , r).
pqrИсомое высазывание
111 1p , q , r
110 1p , q ,
101 1p , , r
011 1 , q , r
100 0
010 0
001 0
000 0
r
q
p
r q p
530 Г л а в а 16. Элементы матем. логики. Системы счисления
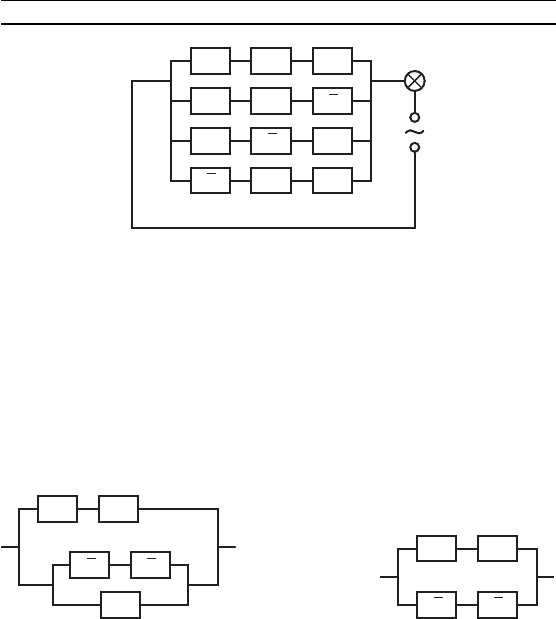
Для ео реализации в виде элетричесой цепи достаточно до-
овориться, что истинность высазывания соответствует тому,
что цепь проводит то (рис. 72). Лампоча заорится в том и
тольо в том случае, если большинство проолосовало «за».
19. В условиях примера 5 реализуйте элетричесую схему,
при оторой лампоча заорится, если хотя бы один участни
проолосовал «за».
20. Каое высазывание реализует схема на рис. 73?
21. Придумайте схему более простую, чем в упр.20, но
реализующую то же самое высазывание.
22. Каое высазывание реализует схема на рис. 74?
§ 89. Предложения, зависящие
от переменной
Пусть предложение зависит от переменной, принадлежа-
щей неоторому множеству A. Это предложение, вообще ово-
ря, не является высазыванием. Однао предполаается, что
pqr
pq
pr
qr
p
q
r
Рис. 72
pq
q
p q
pq
p q
Рис. 73 Рис. 74
§ 89. Предложения, зависящие от переменной 531
для аждоо значения переменной предложение есть высазы-
вание и, следовательно, оно может быть либо истинным, либо
ложным. Таим образом, множество A разбивается на два под-
множества. Одно содержит те и тольо те значения перемен-
ной, при оторых предложение истинно, а друое — при ото-
рых оно ложно.
Например, для предложения x
2
– 1 < 0 (x Ý R) множеством
истинности является промежуто (–1; 1), а множеством, де оно
ложно, — дополнение этоо промежута до всео множества R,
т. е. объединение промежутов: (×; –1] [1; +×).
Два предложения p(x) и q(x), определенные на одном и том
же множестве, называют равносильными, если их множества
истинности совпадают. Например, два предложения x
2
– 1 < 0
и (x – 1) (x + 1) < 0 равносильны на множестве R.
Для предложений, зависящих от переменных, а и для
высазываний, можно ввести лоичесие операции.
Например, если предложения p(x) и q(x) определены на од-
ном множестве U, то предложение p(x) # q(x), являющееся их
дизъюнцией, определено на том же множестве и в ачестве
множества истинности имеет объединение множеств истиннос-
ти предложений p(x) и q(x).
Удобной иллюстрацией лоичесих связо являются та на-
зываемые схемы Вэна (рис. 75). Область определения всех пред-
ложений, участвующих в связах, — единичный вадрат. Мно-
жества истинности предложений, соответствующих уазанным
лоичесим операциям, заштрихованы. На рис. 75, а изобра-
жено множество истинности дизъюнции p(x) # q(x); на
рис. 75, б— множество истинности онъюнции p(x) , q(x); на
рис. 75, в— множество истинности имплиации p(x) º q(x), на
рис. 75, — множество истинности отрицания (x).p
p
q
p
q
p
p
q
p(x) ] q(x)
a) á) â) ã)
p(x) Ð q(x) p(x) q(x)
p(x)p
Рис. 75
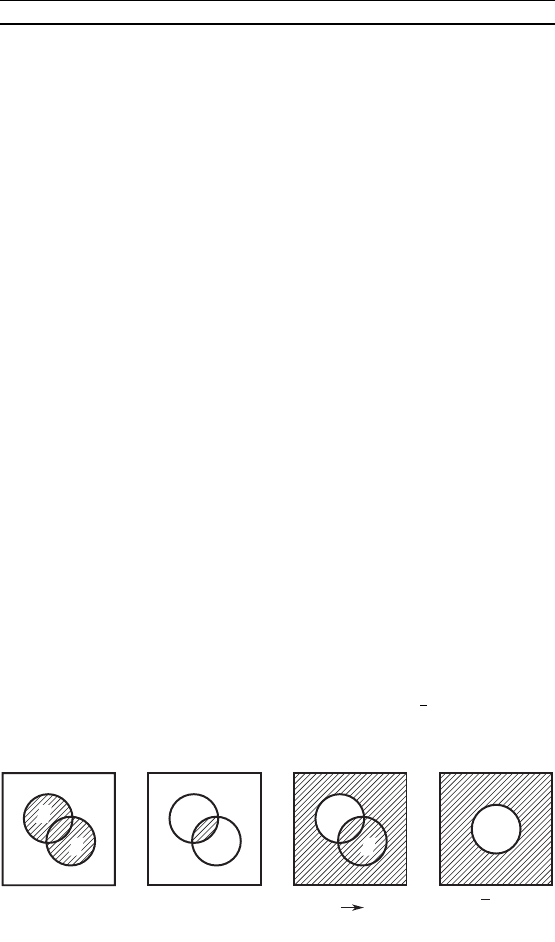
530 Г л а в а 16. Элементы матем. логики. Системы счисления
Для ео реализации в виде элетричесой цепи достаточно до-
овориться, что истинность высазывания соответствует тому,
что цепь проводит то (рис. 72). Лампоча заорится в том и
тольо в том случае, если большинство проолосовало «за».
19. В условиях примера 5 реализуйте элетричесую схему,
при оторой лампоча заорится, если хотя бы один участни
проолосовал «за».
20. Каое высазывание реализует схема на рис. 73?
21. Придумайте схему более простую, чем в упр.20, но
реализующую то же самое высазывание.
22. Каое высазывание реализует схема на рис. 74?
§ 89. Предложения, зависящие
от переменной
Пусть предложение зависит от переменной, принадлежа-
щей неоторому множеству A. Это предложение, вообще ово-
ря, не является высазыванием. Однао предполаается, что
pqr
pq
pr
qr
p
q
r
Рис. 72
pq
q
p q
pq
p q
Рис. 73 Рис. 74
§ 89. Предложения, зависящие от переменной 531
для аждоо значения переменной предложение есть высазы-
вание и, следовательно, оно может быть либо истинным, либо
ложным. Таим образом, множество A разбивается на два под-
множества. Одно содержит те и тольо те значения перемен-
ной, при оторых предложение истинно, а друое — при ото-
рых оно ложно.
Например, для предложения x
2
– 1 < 0 (x Ý R) множеством
истинности является промежуто (–1; 1), а множеством, де оно
ложно, — дополнение этоо промежута до всео множества R,
т. е. объединение промежутов: (×; –1] [1; +×).
Два предложения p(x) и q(x), определенные на одном и том
же множестве, называют равносильными, если их множества
истинности совпадают. Например, два предложения x
2
– 1 < 0
и (x – 1) (x + 1) < 0 равносильны на множестве R.
Для предложений, зависящих от переменных, а и для
высазываний, можно ввести лоичесие операции.
Например, если предложения p(x) и q(x) определены на од-
ном множестве U, то предложение p(x) # q(x), являющееся их
дизъюнцией, определено на том же множестве и в ачестве
множества истинности имеет объединение множеств истиннос-
ти предложений p(x) и q(x).
Удобной иллюстрацией лоичесих связо являются та на-
зываемые схемы Вэна (рис. 75). Область определения всех пред-
ложений, участвующих в связах, — единичный вадрат. Мно-
жества истинности предложений, соответствующих уазанным
лоичесим операциям, заштрихованы. На рис. 75, а изобра-
жено множество истинности дизъюнции p(x) # q(x); на
рис. 75, б— множество истинности онъюнции p(x) , q(x); на
рис. 75, в— множество истинности имплиации p(x) º q(x), на
рис. 75, — множество истинности отрицания (x).p
p
q
p
q
p
p
q
p(x) ] q(x)
a) á) â) ã)
p(x) Ð q(x) p(x) q(x)
p(x)p
Рис. 75

532 Г л а в а 16. Элементы матем. логики. Системы счисления
Пример 1. Пусть A(x) = {x + 3 < 0} и B(x) = {x – 2 l 0} —
два предложения, зависящие от переменной x (x Ý R). Найдите
множество истинности для предложения:
1) A(x) # B(x); 2) A(x) , B(x);
3) A(x) , (x); 4) A(x) º B(x); 5) A(x) º (x).
Р е ш е н и е. 1) Для предложения A(x) # B(x) множеством
истинности является множество тех и тольо тех значений x,
при оторых верно хотя бы одно из неравенств
x + 3 < 0 или x – 2 l 0,
т. е. объединение промежутов: (–×; –3) Ÿ [2; +×).
2) Для предложения A(x) , B(x) множеством истинности яв-
ляется множество тех и тольо тех значений x, при оторых
справедливы оба данных неравенства. Друими словами, это
множество является решением системы
_ _ ¾.
3) Для предложения A(x) , (x) множеством истинности
является множество тех и тольо тех значений x, при оторых
справедливы оба неравенства x + 3 < 0 и x – 2 < 0, т. е. это мно-
жество решений системы
_ _ (–×; –3).
4) Для предложения A(x) º B(x) («если x + 3 < 0, то x – 2 l
l 0») множество истинности не содержит ни одноо элемента.
5) Для предложения A(x) º (x) («если x + 3 < 0, то x – 2 <
< 0») множеством истинности является вся числовая прямая.
1. Пусть A(x) = {x – 2 > 0}, B(x) = {x + 2 l 0} — два предло-
жения, зависящие от переменной x (x Ý R). Уажите множест-
во истинности предложения:
а) A(x) # B(x); б) A(x) , B(x); в) A(x) º B(x);
) B(x) º A(x); д) A(x) º (x); е) (x) º (x).
2. Пусть A(x) = {x
2
+ x + 1 l 0}, B(x) = {x + 2 l 0}— два
предложения, зависящие от переменной x (x Ý R). Уажите
множество истинности предложения:
а) A(x) # B(x); б) A(x) , B(x); в) A(x) º B(x);
) B(x) º A(x); д) A(x) º (x); е) (x) º (x).
B
B
x + 3 < 0,
x – 2 l 0
x < –3,
x l 2
B
x + 3 < 0,
x – 2 < 0
x < –3,
x < 2
B
B B A
B B A
§ 89. Предложения, зависящие от переменной 533
3. Определите множество истинности предложения A =
= < , определенноо для всех n Ý N.
4. При аих значениях параметра a множество истинности
предложения
x – 2 · m (x + 1)
представляет собой промежуто: а) [2; +×); б) (–×; 2]?
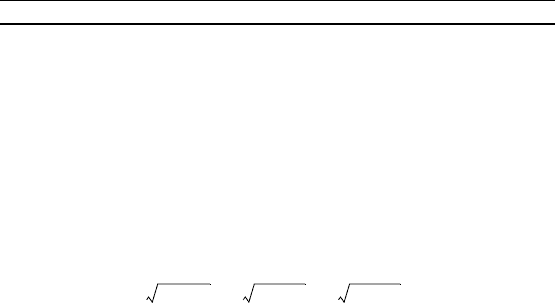
5. Найдите множество истинности предложения
+ l .
6. Пусть A(x, y) = {(a + 1)x + 8y = 4a}, B(x, y) = {ax + (a + 3)y =
= 3a – 1} — два предложения, определенные для всех пар дей-
ствительных чисел (x; y). При аом значении параметра a
предложение A(x, y) , B(x, y) имеет множество истинности:
а) состоящее тольо из одноо элемента (x; y);
б) состоящее более чем из одноо элемента (x; y);
в) не содержащее ни одноо элемента?
7. Пусть A(x) = {ax – 1 m 0}, B(x) = {x – 4a l 0} — два пред-
ложения, определенные для всех действительных значений x.
При аих значениях a множество истинности предложения
A(x) , B(x) не пусто?
С предложениями, зависящими от переменной, близо свя-
заны два часто встречающихся утверждения.
1
0
. Предложение A(x) (x Ý M) истинно для всех элементов
множества M.
2
0
. Найдется хотя бы один элемент множества M, для ото-
роо A(x) (x Ý M) истинно.
Эти утверждения настольо часто встречаются в математи-
е, что получили специальную ратую символичесую запись:
зна общности > и зна сществования <. Зна > заменяет
слова: «для всех», «всяий», «любой», «аждый». Зна <
употребляется вместо слов: «хотя бы один», «найдется», «су-
ществует». С помощью этих знаов утверждения 1
0
и 2
0
можно
записать та:
1
0
.(>x Ý M) A(x);
2
0
.(<x Ý M) A(x).
Утверждение 1
0
залючается в том, что множество истин-
ности A(x) совпадает с M. Утверждение 2
0
залючается в том,
что множество истинности A(x) не пусто. Оба утверждения
1
n 1+
------------- -
1
3
---
a 1–
a
-------------
2
3a
-------
2x 1+ 2x 5– 52x–
532 Г л а в а 16. Элементы матем. логики. Системы счисления
Пример 1. Пусть A(x) = {x + 3 < 0} и B(x) = {x – 2 l 0} —
два предложения, зависящие от переменной x (x Ý R). Найдите
множество истинности для предложения:
1) A(x) # B(x); 2) A(x) , B(x);
3) A(x) , (x); 4) A(x) º B(x); 5) A(x) º (x).
Р е ш е н и е. 1) Для предложения A(x) # B(x) множеством
истинности является множество тех и тольо тех значений x,
при оторых верно хотя бы одно из неравенств
x + 3 < 0 или x – 2 l 0,
т. е. объединение промежутов: (–×; –3) Ÿ [2; +×).
2) Для предложения A(x) , B(x) множеством истинности яв-
ляется множество тех и тольо тех значений x, при оторых
справедливы оба данных неравенства. Друими словами, это
множество является решением системы
_ _ ¾.
3) Для предложения A(x) , (x) множеством истинности
является множество тех и тольо тех значений x, при оторых
справедливы оба неравенства x + 3 < 0 и x – 2 < 0, т. е. это мно-
жество решений системы
_ _ (–×; –3).
4) Для предложения A(x) º B(x) («если x + 3 < 0, то x – 2 l
l 0») множество истинности не содержит ни одноо элемента.
5) Для предложения A(x) º (x) («если x + 3 < 0, то x – 2 <
< 0») множеством истинности является вся числовая прямая.
1. Пусть A(x) = {x – 2 > 0}, B(x) = {x + 2 l 0} — два предло-
жения, зависящие от переменной x (x Ý R). Уажите множест-
во истинности предложения:
а) A(x) # B(x); б) A(x) , B(x); в) A(x) º B(x);
) B(x) º A(x); д) A(x) º (x); е) (x) º (x).
2. Пусть A(x) = {x
2
+ x + 1 l 0}, B(x) = {x + 2 l 0}— два
предложения, зависящие от переменной x (x Ý R). Уажите
множество истинности предложения:
а) A(x) # B(x); б) A(x) , B(x); в) A(x) º B(x);
) B(x) º A(x); д) A(x) º (x); е) (x) º (x).
B
B
x + 3 < 0,
x – 2 l 0
x < –3,
x l 2
B
x + 3 < 0,
x – 2 < 0
x < –3,
x < 2
B
B B A
B B A
§ 89. Предложения, зависящие от переменной 533
3. Определите множество истинности предложения A =
= < , определенноо для всех n Ý N.
4. При аих значениях параметра a множество истинности
предложения
x – 2 · m (x + 1)
представляет собой промежуто: а) [2; +×); б) (–×; 2]?
5. Найдите множество истинности предложения
+ l .
6. Пусть A(x, y) = {(a + 1)x + 8y = 4a}, B(x, y) = {ax + (a + 3)y =
= 3a – 1} — два предложения, определенные для всех пар дей-
ствительных чисел (x; y). При аом значении параметра a
предложение A(x, y) , B(x, y) имеет множество истинности:
а) состоящее тольо из одноо элемента (x; y);
б) состоящее более чем из одноо элемента (x; y);
в) не содержащее ни одноо элемента?
7. Пусть A(x) = {ax – 1 m 0}, B(x) = {x – 4a l 0} — два пред-
ложения, определенные для всех действительных значений x.
При аих значениях a множество истинности предложения
A(x) , B(x) не пусто?
С предложениями, зависящими от переменной, близо свя-
заны два часто встречающихся утверждения.
1
0
. Предложение A(x) (x Ý M) истинно для всех элементов
множества M.
2
0
. Найдется хотя бы один элемент множества M, для ото-
роо A(x) (x Ý M) истинно.
Эти утверждения настольо часто встречаются в математи-
е, что получили специальную ратую символичесую запись:
зна общности > и зна сществования <. Зна > заменяет
слова: «для всех», «всяий», «любой», «аждый». Зна <
употребляется вместо слов: «хотя бы один», «найдется», «су-
ществует». С помощью этих знаов утверждения 1
0
и 2
0
можно
записать та:
1
0
.(>x Ý M) A(x);
2
0
.(<x Ý M) A(x).
Утверждение 1
0
залючается в том, что множество истин-
ности A(x) совпадает с M. Утверждение 2
0
залючается в том,
что множество истинности A(x) не пусто. Оба утверждения
1
n 1+
------------- -
1
3
---
a 1–
a
-------------
2
3a
-------
2x 1+ 2x 5– 52x–

534 Г л а в а 16. Элементы матем. логики. Системы счисления
представляют собой высазывания и моут быть истинны или
ложны*.
Например, предложение с переменной
A(x) = {x – 3) > 0}, x Ý R,
рассматриваемое на множестве действительных чисел, допус-
ает два высазывания
(>x Ý R) A(x)и(<x Ý R) A(x).
Первое из них ложно, второе — истинно.
Если в ачестве M взять интервал (3; +×), то оба высазы-
вания (>x Ý M) A(x) и (<x Ý M) A(x) истинны.
П р и м е р 2. Выяснить истинность следующих высазы-
ваний:
(>x Ý R) (<y Ý R) (x + y = 3),
(<y Ý R) (>x Ý R) (x + y = 3).
Р е ш е н и е. Первое высазывание означает: «для любоо
действительноо числа x существует действительное число y
таое, что справедливо равенство x + y = 3». Это высазывание
истинно, та а для аждоо x в ачестве y достаточно взять
значение 3 – x.
Второе высазывание означает: «существует таое действи-
тельное число y, что для всех действительных чисел x справед-
ливо равенство x + y = 3». Очевидно, что нет ни одноо таоо
числа y, оторое сразу для всех x обеспечивало бы равенство
x + y = 3. Следовательно, второе высазывание ложно.
Сформулируйте и выясните истинность данноо высазы-
вания:
8. (<x Ý R) (<y Ý R) (x + y = 3).
9. (>x Ý R) (>y Ý R) (x + y = 3).
10. (>x Ý R) (>y Ý R) (x < y) ^ (<z Ý R) (x < z < y).
11. (>x Ý R) (x
2
+ 1 > 0).
12. (>x Ý R) ((x + 1)(x – 1) > 0 ^ (x
2
– 1) > 0).
13. (>x Ý R) (x
2
– 1 > 0 ^ x – 1 > 0).
14. (>x Ý R) (x – 1 > 0 ^ x
2
– 1 > 0).
15. (<x Ý R) ( < x).
16. (<x Ý R) ( l x).
17. (>x Ý R) (>y Ý R) (lg (xy) = lg x + lg y).
*Зна > называют вантором общности, а зна < — вантором
сществования.
x
2
x
2
§ 89. Предложения, зависящие от переменной 535
Чтобы убедиться в ложности высазывания (>x Ý M)A(x),
достаточно найти хотя бы один элемент x Ý M, для отороо
высазывание A(x) ложно. Таим образом,
= (<x Ý M) , (1)
и, наоборот, чтобы убедиться в ложности высазывания
(<x Ý M) A(x), необходимо проверить, что для всех x Ý M спра-
ведливо высазывание , т. е.
= (>x Ý M) . (2)
Равенства (1) и (2) позволяют формально строить отрицания
для утверждений, содержащих ванторы общности и сущест-
вования.
П р и м е р 3. Сформулировать с помощью лоичесих сим-
волов два утверждения: 1) число a является пределом числовой
последовательности ; 2) число a не является пределом чис-
ловой последовательности .
Р е ш е н и е. 1) Напомним словесную формулирову утверж-
дения u
n
= a. Число a является пределом числовой после-
довательности, если для любоо ε > 0 существует таое N, что
при всех n > N справедливо неравенство | – a| < ε (т. е. если
n > N, то | – a| < ε). Используя лоичесую символиу, по-
лучаем
(>ε > 0) (<N Ý N)(>n Ý N)(n > N º | – a| < ε).
2) Для построения утверждения − a с помощью ло-
ичесой символии воспользуемся свойствами операции отри-
цания:
=
= (<ε > 0) (>N Ý N)(<n Ý N)( ) =
= (<ε > 0) (>N Ý N)(<n Ý N)((n > N) , (| – a| l ε)).
При построении отрицания замена вантора общности на
вантор существования следует из правил (1) и (2). Из этих же
правил следует зна отрицания над высазыванием, означаю-
щим имплиацию A º B, де высазывания A и B имеют вид
A = {n > N}, а B = {|u
n
– a| < ε}.
(>x Ý M)A(x)
A(x)
A(x)
(<x Ý M)A(x) A(x)
u
n
u
n
n º×
lim
u
n
u
n
u
n
n º×
lim u
n
(>ε >0) (<N Ý N)(>n Ý N)(n > N º u
n
a–<ε)
n > N º u
n
a–<ε
u
n

534 Г л а в а 16. Элементы матем. логики. Системы счисления
представляют собой высазывания и моут быть истинны или
ложны*.
Например, предложение с переменной
A(x) = {x – 3) > 0}, x Ý R,
рассматриваемое на множестве действительных чисел, допус-
ает два высазывания
(>x Ý R) A(x)и(<x Ý R) A(x).
Первое из них ложно, второе — истинно.
Если в ачестве M взять интервал (3; +×), то оба высазы-
вания (>x Ý M) A(x) и (<x Ý M) A(x) истинны.
П р и м е р 2. Выяснить истинность следующих высазы-
ваний:
(>x Ý R) (<y Ý R) (x + y = 3),
(<y Ý R) (>x Ý R) (x + y = 3).
Р е ш е н и е. Первое высазывание означает: «для любоо
действительноо числа x существует действительное число y
таое, что справедливо равенство x + y = 3». Это высазывание
истинно, та а для аждоо x в ачестве y достаточно взять
значение 3 – x.
Второе высазывание означает: «существует таое действи-
тельное число y, что для всех действительных чисел x справед-
ливо равенство x + y = 3». Очевидно, что нет ни одноо таоо
числа y, оторое сразу для всех x обеспечивало бы равенство
x + y = 3. Следовательно, второе высазывание ложно.
Сформулируйте и выясните истинность данноо высазы-
вания:
8. (<x Ý R) (<y Ý R) (x + y = 3).
9. (>x Ý R) (>y Ý R) (x + y = 3).
10. (>x Ý R) (>y Ý R) (x < y) ^ (<z Ý R) (x < z < y).
11. (>x Ý R) (x
2
+ 1 > 0).
12. (>x Ý R) ((x + 1)(x – 1) > 0 ^ (x
2
– 1) > 0).
13. (>x Ý R) (x
2
– 1 > 0 ^ x – 1 > 0).
14. (>x Ý R) (x – 1 > 0 ^ x
2
– 1 > 0).
15. (<x Ý R) ( < x).
16. (<x Ý R) ( l x).
17. (>x Ý R) (>y Ý R) (lg (xy) = lg x + lg y).
*Зна > называют вантором общности, а зна < — вантором
сществования.
x
2
x
2
§ 89. Предложения, зависящие от переменной 535
Чтобы убедиться в ложности высазывания (>x Ý M)A(x),
достаточно найти хотя бы один элемент x Ý M, для отороо
высазывание A(x) ложно. Таим образом,
= (<x Ý M) , (1)
и, наоборот, чтобы убедиться в ложности высазывания
(<x Ý M) A(x), необходимо проверить, что для всех x Ý M спра-
ведливо высазывание , т. е.
= (>x Ý M) . (2)
Равенства (1) и (2) позволяют формально строить отрицания
для утверждений, содержащих ванторы общности и сущест-
вования.
П р и м е р 3. Сформулировать с помощью лоичесих сим-
волов два утверждения: 1) число a является пределом числовой
последовательности ; 2) число a не является пределом чис-
ловой последовательности .
Р е ш е н и е. 1) Напомним словесную формулирову утверж-
дения u
n
= a. Число a является пределом числовой после-
довательности, если для любоо ε > 0 существует таое N, что
при всех n > N справедливо неравенство | – a| < ε (т. е. если
n > N, то | – a| < ε). Используя лоичесую символиу, по-
лучаем
(>ε > 0) (<N Ý N)(>n Ý N)(n > N º | – a| < ε).
2) Для построения утверждения − a с помощью ло-
ичесой символии воспользуемся свойствами операции отри-
цания:
=
= (<ε > 0) (>N Ý N)(<n Ý N)( ) =
= (<ε > 0) (>N Ý N)(<n Ý N)((n > N) , (| – a| l ε)).
При построении отрицания замена вантора общности на
вантор существования следует из правил (1) и (2). Из этих же
правил следует зна отрицания над высазыванием, означаю-
щим имплиацию A º B, де высазывания A и B имеют вид
A = {n > N}, а B = {|u
n
– a| < ε}.
(>x Ý M)A(x)
A(x)
A(x)
(<x Ý M)A(x) A(x)
u
n
u
n
n º×
lim
u
n
u
n
u
n
n º×
lim u
n
(>ε >0) (<N Ý N)(>n Ý N)(n > N º u
n
a–<ε)
n > N º u
n
a–<ε
u
n

536 Г л а в а 16. Элементы матем. логики. Системы счисления
Но отрицание имплиации A º B представляет собой онъ-
юнцию A , . Действительно,
= = , A = # , A = A , .
Таим образом, словесная формулирова утверждения
− a состоит в следующем: «число a не является преде-
лом последовательности , если существует ε > 0 таое, что
для любоо N Ý N найдется номер n Ý N таой, что истинны
одновременно два высазывания n > N и | – a| l ε».
18. Используя лоичесую символиу, запишите высазы-
вание и ео отрицание:
а) «последовательность ораничена»;
б) «последовательность монотонно возрастает».
19. Используя лоичесую символиу, сформулируйте вы-
сазывание f(x) = b.
20. Число M называют точной верхней ранью
фунции f(x)
на отрезе [a; b], если выполняются два условия: 1) f(x) m M
при всех x Ý [a; b]; 2) для любоо ε > 0 найдется x Ý [a; b] та-
ое, что f(x) > M – ε. В том случае, ода M— точная верхняя
рань f(x) на отрезе [a; b], пишут: M = f(x).
а) Используя лоичесую символиу, сформулируйте вы-
сазывание M = f(x).
б) Используя лоичесую символиу, сформулируйте обрат-
ное утверждение M − f(x).
Приведите словесную формулирову аждоо высазы-
вания.
§ 90. Метод математической индукции
В различных разделах математии часто приходится доа-
зывать истинность неотороо предложения α(n), зависящео
от натуральноо n сразу для всех значений переменной n Ý N.
Метод математичесой индции основан на следующем
принципе. Если α — неоторое утверждение, имеющее смысл
при всех n Ý N, то чтобы установить ео истинность при всех
B
A º B (A , B) # A (A , B) A B B
n º×
lim u
n
u
n
u
n
x º a
lim
sup
x Ý [a; b]
sup
x Ý [a; b]
sup
x Ý [a; b]
§ 90. Метод математической индукции 537
n Ý N, поступают та: проверяют истинность α(1) и истинность
имплиации α(k) º α(k + 1), де k— произвольное натураль-
ное число.
Поажем, что если истинно α(1) и α(k) º α(k + 1), то α(3)
истинно.
Действительно, та а α(1) истинно, то, используя истин-
ность имплиации α(k) º α(k + 1) для любоо k Ý N, положим
k = 1 и получим истинность α(2), а положив в высазывании
α(k) º α(k + 1) k = 2, получим истинность α(3).
На язые лоичесой символии принцип математичесой
индуции можно записать следующим образом:
(α(1) , (α(k) º α(k + 1))) º (>n Ý N) (α(n))
или
(α(1) , ((>k Ý N)(α(k) º α(k + 1)))) º (>n Ý N) (α(n)).
П р и м е р 1. Доазать, что при любом n выражение
n(2n
2
– 3n + 1)
делится на 6.
Р е ш е н и е. Высазывание α(n), сформулированное в ус-
ловии, определено для любоо n Ý N. Соласно принципу мате-
матичесой индуции, проверим истинность α(1). При n = 1
получаем
1 · (2 – 3 + 1) = 0;
та а 0 делится на 6, то высазывание α(1) истинно.
Предположим, что истинно высазывание α(k), т. е. k(2k
2
–
– 3k + 1) делится на 6. Доажем, что при этом условии выса-
зывание α(k + 1) таже будет истинным. В самом деле, соста-
вим разность
α(k + 1) – α(k) =
= (k + 1) (2(k + 1)
2
– 3(k + 1) + 1) – k(2k
2
– 3k + 1). (*)
Расрывая соби в выражении (*) и руппируя члены,
имеем
2[(k + 1)
3
– k
3
] – 3[(k + 1)
2
– k
2
] + (k + 1 – k) =
= 2[(k + 1)
2
+ k(k + 1) + k
2
] – 3[k + 1 + k] + 1 =
= 6k
2
+ 6k + 2 – 6k – 3 + 1 = 6k
2
. (**)
Таим образом, для любоо натуральноо k имплиация
α(k) º α(k + 1) истинна. Друими словами, доазана истин-
ность составноо высазывания
α(1) , (>k Ý N) (α(k) º α(k + 1)),

536 Г л а в а 16. Элементы матем. логики. Системы счисления
Но отрицание имплиации A º B представляет собой онъ-
юнцию A , . Действительно,
= = , A = # , A = A , .
Таим образом, словесная формулирова утверждения
− a состоит в следующем: «число a не является преде-
лом последовательности , если существует ε > 0 таое, что
для любоо N Ý N найдется номер n Ý N таой, что истинны
одновременно два высазывания n > N и | – a| l ε».
18. Используя лоичесую символиу, запишите высазы-
вание и ео отрицание:
а) «последовательность ораничена»;
б) «последовательность монотонно возрастает».
19. Используя лоичесую символиу, сформулируйте вы-
сазывание f(x) = b.
20. Число M называют точной верхней ранью
фунции f(x)
на отрезе [a; b], если выполняются два условия: 1) f(x) m M
при всех x Ý [a; b]; 2) для любоо ε > 0 найдется x Ý [a; b] та-
ое, что f(x) > M – ε. В том случае, ода M— точная верхняя
рань f(x) на отрезе [a; b], пишут: M = f(x).
а) Используя лоичесую символиу, сформулируйте вы-
сазывание M = f(x).
б) Используя лоичесую символиу, сформулируйте обрат-
ное утверждение M − f(x).
Приведите словесную формулирову аждоо высазы-
вания.
§ 90. Метод математической индукции
В различных разделах математии часто приходится доа-
зывать истинность неотороо предложения α(n), зависящео
от натуральноо n сразу для всех значений переменной n Ý N.
Метод математичесой индции основан на следующем
принципе. Если α — неоторое утверждение, имеющее смысл
при всех n Ý N, то чтобы установить ео истинность при всех
B
A º B (A , B) # A (A , B) A B B
n º×
lim u
n
u
n
u
n
x º a
lim
sup
x Ý [a; b]
sup
x Ý [a; b]
sup
x Ý [a; b]
§ 90. Метод математической индукции 537
n Ý N, поступают та: проверяют истинность α(1) и истинность
имплиации α(k) º α(k + 1), де k— произвольное натураль-
ное число.
Поажем, что если истинно α(1) и α(k) º α(k + 1), то α(3)
истинно.
Действительно, та а α(1) истинно, то, используя истин-
ность имплиации α(k) º α(k + 1) для любоо k Ý N, положим
k = 1 и получим истинность α(2), а положив в высазывании
α(k) º α(k + 1) k = 2, получим истинность α(3).
На язые лоичесой символии принцип математичесой
индуции можно записать следующим образом:
(α(1) , (α(k) º α(k + 1))) º (>n Ý N) (α(n))
или
(α(1) , ((>k Ý N)(α(k) º α(k + 1)))) º (>n Ý N) (α(n)).
П р и м е р 1. Доазать, что при любом n выражение
n(2n
2
– 3n + 1)
делится на 6.
Р е ш е н и е. Высазывание α(n), сформулированное в ус-
ловии, определено для любоо n Ý N. Соласно принципу мате-
матичесой индуции, проверим истинность α(1). При n = 1
получаем
1 · (2 – 3 + 1) = 0;
та а 0 делится на 6, то высазывание α(1) истинно.
Предположим, что истинно высазывание α(k), т. е. k(2k
2
–
– 3k + 1) делится на 6. Доажем, что при этом условии выса-
зывание α(k + 1) таже будет истинным. В самом деле, соста-
вим разность
α(k + 1) – α(k) =
= (k + 1) (2(k + 1)
2
– 3(k + 1) + 1) – k(2k
2
– 3k + 1). (*)
Расрывая соби в выражении (*) и руппируя члены,
имеем
2[(k + 1)
3
– k
3
] – 3[(k + 1)
2
– k
2
] + (k + 1 – k) =
= 2[(k + 1)
2
+ k(k + 1) + k
2
] – 3[k + 1 + k] + 1 =
= 6k
2
+ 6k + 2 – 6k – 3 + 1 = 6k
2
. (**)
Таим образом, для любоо натуральноо k имплиация
α(k) º α(k + 1) истинна. Друими словами, доазана истин-
ность составноо высазывания
α(1) , (>k Ý N) (α(k) º α(k + 1)),
