Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.

478 Г л а в а 14. Метод координат и элементы векторной алгебры
Та а = + и, следоваетльно,
= ( + ),
то
= ( + ) – = – .
Сравнивая разложения веторов и по неоллинеарным
веторам и , залючаем, что = λ , де λ = .
Та а веторы и оллинеарны и имеют общее нача-
ло, то три точи A, B, C лежат на одной прямой.
1. На прямых BC, CA, AB, определяющих треуольни ABC,
взяты соответственно точи L, M и N, лежащие на одной пря-
мой. Доажите, что если
= α , = β , = γ ,
то αβγ = –1 (теорема Менелая
).
2. Дан треуольни MNP. На прямых MN, NP, PM взяты
точи A, B и C та, что = α , = β , = γ .
Доажите, что если αβγ = –1, то точи A, B, C лежат на одной
прямой (обратная теорема Менелая
).
3. Прямые a и b параллельны. На прямой a взяты произ-
вольные точи A
1
, A
2
, A
3
, на прямой b— произвольные точи
B
1
, B
2
, B
3
. На отрезах A
1
B
1
, A
2
B
2
, A
3
B
3
взяты таие точи C
1
,
C
2
, C
3
, что
A
1
C
1
= αA
1
B
1
, A
2
C
2
= αA
2
B
2
, A
3
C
3
= αA
3
B
3
.
Доажите, что точи C
1
, C
2
, C
3
лежат на одной прямой.
4. Точи C
1
, C
2
, C
3
делят отрезо AB на четыре части; D—
произвольная точа плосости. Выразите веторы , ,
через веторы = , = .
5. Даны три точи M, A, B, а четвертая точа C взята та,
что = 3 . Выразите ветор через веторы и .
6. На плосости взяты три точи A, B, M. На отрезе AB
взята таая точа C, что AC : CB = k. Выразите ветор
через и .
OM
OA ON
1
n 1+
------------- -
OM
1
n 1+
------------- -
OA ON
AC
1
n 1+
------------- -
OA ON OA
1
n 1+
------------- -
ON
n
n 1+
------------- -
OA
AB AC
ON OA AB AC
n 1+
n
------------- -
AB AC
BL LC CM MA AN NB
MA AN NB BP PC CM
DC
1
DC
2
DC
3
DA a DB b
AB AC MC MA MB
MC
MA MB
§ 80. Решение геометрических задач методами векторной алгебры 479
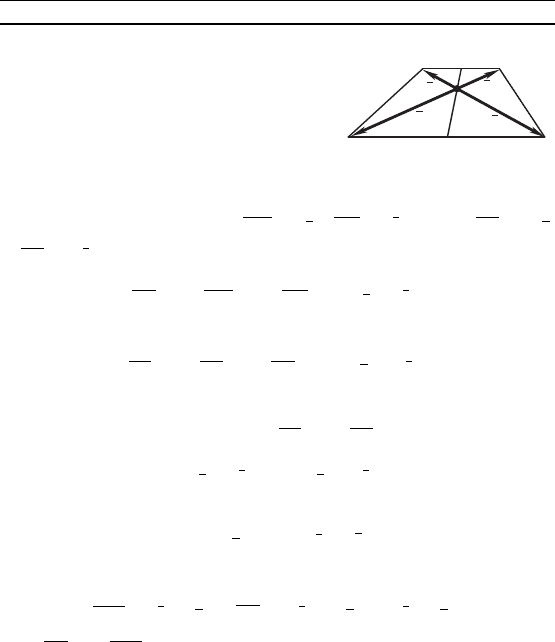
Пример 3. Доазать, что ес-
ли точа A пересечения диаоналей
четырехуольниа MNPQ и середи-
ны B, C ео противоположных сто-
рон MN, PQ лежат на одной пря-
мой, то MNPQ — трапеция или па-
раллелорамм (рис. 68).
Р е ш е н и е. Положим = , = . Тода = k
и = l . Та а B— середина отреза MN, то
= + = ( + ).
Аналоично
= + = (k + l ).
По условию точи A, B, C лежат на одной прямой, и значит,
существует таое число m, что = m , т. е.
( + ) = (k + l ),
или
+ = ,
отуда следует, что m = k = l. Тода
= – , = l – k = k( – ),
т. е. = k . Следовательно, PQ Ï MN, т. е. MNPQ — тра-
пеция или параллелорамм.
17. Точа пересечения «средних линий» четырехуольниа
(отрезов, соединяющих середины ео сторон) совпадает с точ-
ой пересечения ео диаоналей. Доажите, что таой четы-
рехуольни — параллелорамм.
18. Доажите, что середины оснований трапеции и точа
пересечения продолжений ее боовых сторон принадлежат од-
ной прямой.
19. Точа M— середина отреза AB, точа — середина
отреза . Доажите, что середины отрезов , и
расположены на одной прямой.
10. Доажите, что середины сторон произвольноо четырех-
уольниа являются вершинами параллелорамма.
lb
QC
ka
a
b
A
MBN
P
Рис. 68
AM
a AN b AP a
AQ b
AB
1
2
---
AM
1
2
---
AN
1
2
---
a b
AC
1
2
---
AP
1
2
---
AQ
1
2
---
a b
AC AB
m
2
---- -
a b
1
2
---
a b
mk–
2
---------------
a
ml–
2
-------------
b 0
MN b a PQ b a b a
PQ MN
M
′
A
′
B
′
AA
′
BB
′
MM
′
478 Г л а в а 14. Метод координат и элементы векторной алгебры
Та а = + и, следоваетльно,
= ( + ),
то
= ( + ) – = – .
Сравнивая разложения веторов и по неоллинеарным
веторам и , залючаем, что = λ , де λ = .
Та а веторы и оллинеарны и имеют общее нача-
ло, то три точи A, B, C лежат на одной прямой.
1. На прямых BC, CA, AB, определяющих треуольни ABC,
взяты соответственно точи L, M и N, лежащие на одной пря-
мой. Доажите, что если
= α , = β , = γ ,
то αβγ = –1 (теорема Менелая
).
2. Дан треуольни MNP. На прямых MN, NP, PM взяты
точи A, B и C та, что = α , = β , = γ .
Доажите, что если αβγ = –1, то точи A, B, C лежат на одной
прямой (обратная теорема Менелая
).
3. Прямые a и b параллельны. На прямой a взяты произ-
вольные точи A
1
, A
2
, A
3
, на прямой b— произвольные точи
B
1
, B
2
, B
3
. На отрезах A
1
B
1
, A
2
B
2
, A
3
B
3
взяты таие точи C
1
,
C
2
, C
3
, что
A
1
C
1
= αA
1
B
1
, A
2
C
2
= αA
2
B
2
, A
3
C
3
= αA
3
B
3
.
Доажите, что точи C
1
, C
2
, C
3
лежат на одной прямой.
4. Точи C
1
, C
2
, C
3
делят отрезо AB на четыре части; D—
произвольная точа плосости. Выразите веторы , ,
через веторы = , = .
5. Даны три точи M, A, B, а четвертая точа C взята та,
что = 3 . Выразите ветор через веторы и .
6. На плосости взяты три точи A, B, M. На отрезе AB
взята таая точа C, что AC : CB = k. Выразите ветор
через и .
OM
OA ON
1
n 1+
------------- -
OM
1
n 1+
------------- -
OA ON
AC
1
n 1+
------------- -
OA ON OA
1
n 1+
------------- -
ON
n
n 1+
------------- -
OA
AB AC
ON OA AB AC
n 1+
n
------------- -
AB AC
BL LC CM MA AN NB
MA AN NB BP PC CM
DC
1
DC
2
DC
3
DA a DB b
AB AC MC MA MB
MC
MA MB
§ 80. Решение геометрических задач методами векторной алгебры 479
Пример 3. Доазать, что ес-
ли точа A пересечения диаоналей
четырехуольниа MNPQ и середи-
ны B, C ео противоположных сто-
рон MN, PQ лежат на одной пря-
мой, то MNPQ — трапеция или па-
раллелорамм (рис. 68).
Р е ш е н и е. Положим = , = . Тода = k
и = l . Та а B— середина отреза MN, то
= + = ( + ).
Аналоично
= + = (k + l ).
По условию точи A, B, C лежат на одной прямой, и значит,
существует таое число m, что = m , т. е.
( + ) = (k + l ),
или
+ = ,
отуда следует, что m = k = l. Тода
= – , = l – k = k( – ),
т. е. = k . Следовательно, PQ Ï MN, т. е. MNPQ — тра-
пеция или параллелорамм.
17. Точа пересечения «средних линий» четырехуольниа
(отрезов, соединяющих середины ео сторон) совпадает с точ-
ой пересечения ео диаоналей. Доажите, что таой четы-
рехуольни — параллелорамм.
18. Доажите, что середины оснований трапеции и точа
пересечения продолжений ее боовых сторон принадлежат од-
ной прямой.
19. Точа M— середина отреза AB, точа — середина
отреза . Доажите, что середины отрезов , и
расположены на одной прямой.
10. Доажите, что середины сторон произвольноо четырех-
уольниа являются вершинами параллелорамма.
lb
QC
ka
a
b
A
MBN
P
Рис. 68
AM
a AN b AP a
AQ b
AB
1
2
---
AM
1
2
---
AN
1
2
---
a b
AC
1
2
---
AP
1
2
---
AQ
1
2
---
a b
AC AB
m
2
---- -
a b
1
2
---
a b
mk–
2
---------------
a
ml–
2
-------------
b 0
MN b a PQ b a b a
PQ MN
M
′
A
′
B
′
AA
′
BB
′
MM
′
480 Г л а в а 14. Метод координат и элементы векторной алгебры
11. Доажите, что в произвольном четырехуольние:
а) «средние линии», пересеаясь, делятся пополам;
б) отрезо, соединяющий середины диаоналей, проходит
через точу пересечения «средних линий» и делится в этой
точе пополам.
При решении ряда задач используют формулу
= ( + + ), (2)
де A, B, C— произвольные точи, не лежащие на одной пря-
мой; M— центр тяжести треуольниа ABC; O— произволь-
ная точа.
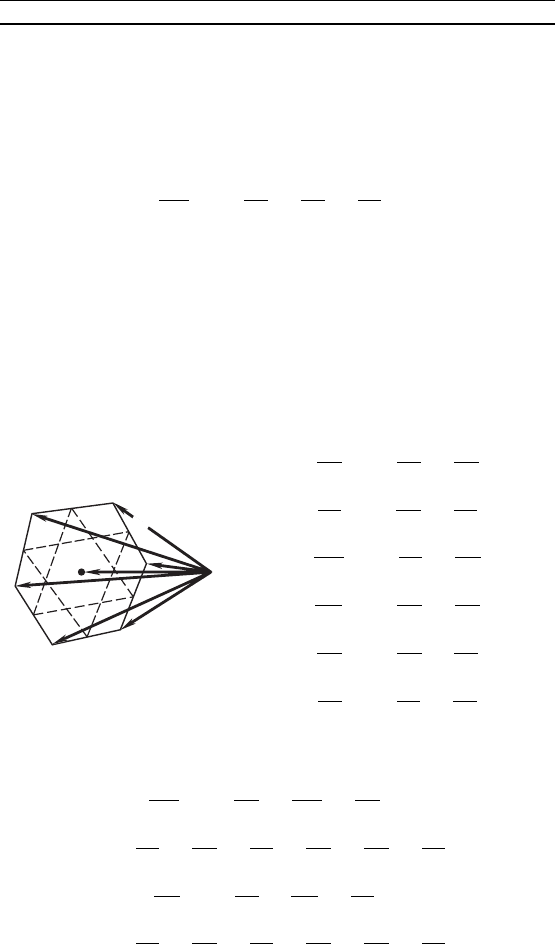
Пример 4. Пусть ABCDEF — произвольный шести-
уольни и U, V, W, X, Y, Z— середины ео сторон. Доазать,
что центры тяжести треуольниов UWY и VXZ совпадают
(рис. 69).
Р е ш е н и е. Та а точи U, V, W, X, Y и Z— середины
сторон шестиуольниа, то
= ( + ),
= ( + ),
= ( + ),
= ( + ),
= ( + ),
= ( + ),
де O— произвольная точа. Обозначив через M и N центры
тяжести треуольниов UWY и VXZ, по формуле (2) находим
= ( + + ) =
= ( + + + + + ),
= ( + + ) =
= ( + + + + + ).
OM
1
3
---
OA OB OC
O
C
A
M
B
N
D
X
Y
E
F
Z
U
V
W
Рис. 69
OU
1
2
---
OA OB
OV
1
2
---
OB OC
OW
1
2
---
OC OD
OX
1
2
---
OD OE
OY
1
2
---
OE OF
OZ
1
2
---
OF OA
OM
1
3
---
OU OW OY
1
6
---
OA OB OC OD OE OF
ON
1
3
---
OV OX OZ
1
6
---
OA OB OC OD OE OF
§ 80. Решение геометрических задач методами векторной алгебры 481
Таим образом, = , отуда следует, что точа M
совпадает с точой N.
12. Дан треуольни ABC. Доажите, что равенство +
+ + = имеет место в том и тольо том случае, ода
O— центр тяжести треуольниа ABC.
13. а) Пусть M и N— центры тяжести треуольниов ABC и
DEF. Доажите, что + + = 3 .
б) Пусть A, B, C, D, E, F— произвольные точи плосости.
Доажите, что + + = + + .
14. Точа M— центр тяжести треуольниа ABC. Доажи-
те, что + = 3 .
15. Через центр тяжести треуольниа ABC проведена пря-
мая l, пересеающая стороны AC и BC соответственно в точах
P и Q. Доажите, что + = 1.
16. Вершины A
1
, B
1
, C
1
треуольниа A
1
B
1
C
1
принадлежат
трем различным сторонам треуольниа ABC, причем центры тя-
жести обоих треуольниов совпадают. Доажите, что точи A
1
,
B
1
и C
1
делят стороны треуольниа ABC в равных отношениях.
При решении задач, связанных с вычислением отношения
площадей неоторых плосих фиур, используют следующее
свойство площадей треуольниов
: если площадь треуольни-
а ABC равна S и на сторонах AC и BC этоо треуольниа
выбраны соответственно точи M и N та, что
CM : CA = k
1
, CN : CB = k
2
,
то площадь треуольниа MCN равна k
1
k
2
S.
П р и м е р 5. В треуольние ABC
на стороне AB взята точа K та, что
AK : BK = 1 : 2, а на стороне BC — точ-
а L та, что CL : BL = 2 : 1 (рис. 70).
Пусть Q— точа пересечения прямых
AL и CK. Найти площадь треуольниа
ABC, если известно, что площадь тре-
уольниа BQC равна 1.
Р е ш е н и е. Пусть = , =
(рис. 70). Та а BL : LC = 1 : 2, то со-
OM
ON
OA
OB OC 0
AD BE CF MN
AD BE CF AE BF CD
CA CB CM
AP
PC
--------
BQ
QC
-------- -
Q
C
A
M
B
N
K
L
Рис. 70
AB
a AC b

480 Г л а в а 14. Метод координат и элементы векторной алгебры
11. Доажите, что в произвольном четырехуольние:
а) «средние линии», пересеаясь, делятся пополам;
б) отрезо, соединяющий середины диаоналей, проходит
через точу пересечения «средних линий» и делится в этой
точе пополам.
При решении ряда задач используют формулу
= ( + + ), (2)
де A, B, C— произвольные точи, не лежащие на одной пря-
мой; M— центр тяжести треуольниа ABC; O— произволь-
ная точа.
Пример 4. Пусть ABCDEF — произвольный шести-
уольни и U, V, W, X, Y, Z— середины ео сторон. Доазать,
что центры тяжести треуольниов UWY и VXZ совпадают
(рис. 69).
Р е ш е н и е. Та а точи U, V, W, X, Y и Z— середины
сторон шестиуольниа, то
= ( + ),
= ( + ),
= ( + ),
= ( + ),
= ( + ),
= ( + ),
де O— произвольная точа. Обозначив через M и N центры
тяжести треуольниов UWY и VXZ, по формуле (2) находим
= ( + + ) =
= ( + + + + + ),
= ( + + ) =
= ( + + + + + ).
OM
1
3
---
OA OB OC
O
C
A
M
B
N
D
X
Y
E
F
Z
U
V
W
Рис. 69
OU
1
2
---
OA OB
OV
1
2
---
OB OC
OW
1
2
---
OC OD
OX
1
2
---
OD OE
OY
1
2
---
OE OF
OZ
1
2
---
OF OA
OM
1
3
---
OU OW OY
1
6
---
OA OB OC OD OE OF
ON
1
3
---
OV OX OZ
1
6
---
OA OB OC OD OE OF
§ 80. Решение геометрических задач методами векторной алгебры 481
Таим образом, = , отуда следует, что точа M
совпадает с точой N.
12. Дан треуольни ABC. Доажите, что равенство +
+ + = имеет место в том и тольо том случае, ода
O— центр тяжести треуольниа ABC.
13. а) Пусть M и N— центры тяжести треуольниов ABC и
DEF. Доажите, что + + = 3 .
б) Пусть A, B, C, D, E, F— произвольные точи плосости.
Доажите, что + + = + + .
14. Точа M— центр тяжести треуольниа ABC. Доажи-
те, что + = 3 .
15. Через центр тяжести треуольниа ABC проведена пря-
мая l, пересеающая стороны AC и BC соответственно в точах
P и Q. Доажите, что + = 1.
16. Вершины A
1
, B
1
, C
1
треуольниа A
1
B
1
C
1
принадлежат
трем различным сторонам треуольниа ABC, причем центры тя-
жести обоих треуольниов совпадают. Доажите, что точи A
1
,
B
1
и C
1
делят стороны треуольниа ABC в равных отношениях.
При решении задач, связанных с вычислением отношения
площадей неоторых плосих фиур, используют следующее
свойство площадей треуольниов
: если площадь треуольни-
а ABC равна S и на сторонах AC и BC этоо треуольниа
выбраны соответственно точи M и N та, что
CM : CA = k
1
, CN : CB = k
2
,
то площадь треуольниа MCN равна k
1
k
2
S.
П р и м е р 5. В треуольние ABC
на стороне AB взята точа K та, что
AK : BK = 1 : 2, а на стороне BC — точ-
а L та, что CL : BL = 2 : 1 (рис. 70).
Пусть Q— точа пересечения прямых
AL и CK. Найти площадь треуольниа
ABC, если известно, что площадь тре-
уольниа BQC равна 1.
Р е ш е н и е. Пусть = , =
(рис. 70). Та а BL : LC = 1 : 2, то со-
OM
ON
OA
OB OC 0
AD BE CF MN
AD BE CF AE BF CD
CA CB CM
AP
PC
--------
BQ
QC
-------- -
Q
C
A
M
B
N
K
L
Рис. 70
AB
a AC b
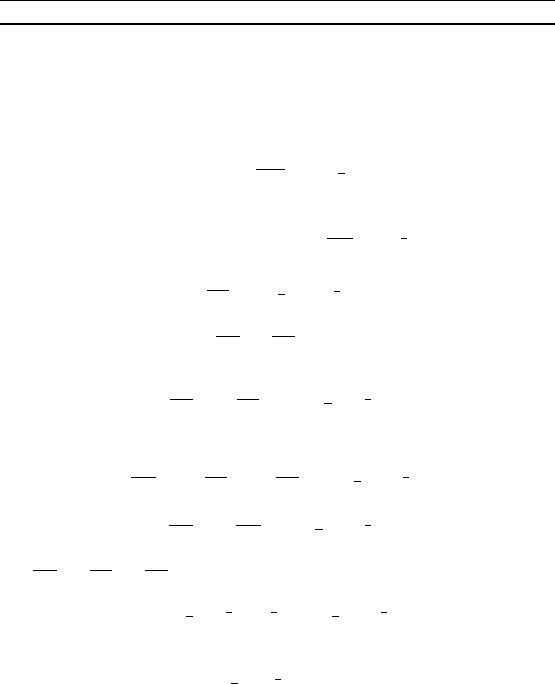
482 Г л а в а 14. Метод координат и элементы векторной алгебры
ласно сформулированному выше свойству площадей получаем
S
BQL
= , S
LQC
= .
Найдем отношение QL : AL. Прямая, проходящая через точ-
у L параллельно стороне AC, пересечет сторону AB в точе M,
причем AM : MB = 2 : 1 и = . Прямая, проходящая
через точу L параллельно стороне AB, пересечет сторону AC
в точе N, причем AN : NC = 1 : 2 и = . Отсюда
= + .
Учитывая, что веторы и оллинеарны (точи A, Q, L
лежат на одной прямой), имеем
= µ = (2 + ). (*)
Аналоично для точи K находим
= + = ( – 3 ),
= λ = ( – 3 ).
Но = + , отуда
(2 + ) = + ( – 3 ).
Из условия единственности разложения ветора по двум не-
оллинеарным веторам и получаем систему уравнений
2µ = λ, µ = 3 – 3λ, из оторой находим µ = .
Теперь можно найти отношение QL : AL. Имеем
= = 1 – ,
и в силу равенства (*) получим = 1 – µ = . Отсюда =
= = ; та а S
QBC
= 1, то исомая площадь равна .
Ответ..
1
3
---
2
3
---
AM
2
3
---
a
AN
1
3
---
b
AL
2
3
---
a
1
3
---
b
AQ AL
AQ AL
µ
3
---
a b
CK
2
3
---
CA
1
3
---
CB
1
3
---
a b
CQ CK
λ
3
---
a b
AQ AC CQ
µ
3
---
a b b
λ
3
---
a b
a b
3
7
---
QL
AL
--------
AL AQ–
AL
----------------------- -
AQ
AL
-------- -
QL
AL
--------
4
7
---
S
ABC
S
QBC
------------------ -
1
1 µ–
-------------
7
4
---
7
4
---
7
4
---
§ 80. Решение геометрических задач методами векторной алгебры 483
17. В треуольние ABC, площадь отороо равна 6, на сто-
роне AB взята точа K, делящая эту сторону в отношении
AK : BK = 2 : 3, а на стороне AC — точа L, делящая AC в отноше-
нии AL : LC = 5 : 3. Точа Q пересечения прямых CK и BL отсто-
ит от прямой AB на расстояние 1,5. Найдите длину стороны AB.
18. Дан треуольни ABC. На сторонах AB и BC взяты точ-
и M и N соответственно та, что AB = 5AM, BC = 3BN. Отрез-
и AN и CM пересеаются в точе O. Найдите отношение пло-
щадей треуольниов AOC и ABC.
19. Точа K делит медиану AD треуольниа ABC в отноше-
нии 3 : 1, считая от вершины. В аом отношении прямая BK
делит площадь треуольниа ABC?
20. На аждой медиане треуольниа взята точа, делящая
медиану в отношении 1 : 3, считая от вершины. Найдите отно-
шение площади треуольниа с вершинами в этих точах пло-
щади исходноо треуольниа.
Решение неоторых задач основано на использовании вето-
ра , оллинеарноо биссетрисе ула между веторами и .
При этом бывает удобно представить ветор в следующем виде:
= + . (3)
21. В треуольние ABC даны стороны a, b, c. Найдите ,
де AA
1
— биссетриса внутреннео ула A треуольниа.
22. В треуольние ABC медиана BD пересеается с биссе-
трисой AF в точе O. Отношение площади треуольниа DOA
площади треуольниа BOF равно . Найдите AC : AB.
23. В треуольние ABC биссетриса AD делит сторону BC
в отношении BD : CD = 2 : 1. В аом отношении медиана CE
делит эту биссетрису?
24. Биссетрисы AD и BE треуольниа ABC пересеаются
в точе O. Найдите отношение площади треуольниа ABC пло-
щади четырехуольниа ODCE, если BC = a, AC = b, AB = c.
Решение неоторых задач основано на использовании сле-
дующео веторноо соотношения
: если A, B, C, D— четыре
точи, принадлежащие одной плосости, а O — произвольная
точа пространства, то
= α + β + (1 – α – β), (4)
де α Ý R, β Ý R.
c
a b
c
c
a
a
------
b
b
-----
AA
1
3
8
---
OD OA OB OC
482 Г л а в а 14. Метод координат и элементы векторной алгебры
ласно сформулированному выше свойству площадей получаем
S
BQL
= , S
LQC
= .
Найдем отношение QL : AL. Прямая, проходящая через точ-
у L параллельно стороне AC, пересечет сторону AB в точе M,
причем AM : MB = 2 : 1 и = . Прямая, проходящая
через точу L параллельно стороне AB, пересечет сторону AC
в точе N, причем AN : NC = 1 : 2 и = . Отсюда
= + .
Учитывая, что веторы и оллинеарны (точи A, Q, L
лежат на одной прямой), имеем
= µ = (2 + ). (*)
Аналоично для точи K находим
= + = ( – 3 ),
= λ = ( – 3 ).
Но = + , отуда
(2 + ) = + ( – 3 ).
Из условия единственности разложения ветора по двум не-
оллинеарным веторам и получаем систему уравнений
2µ = λ, µ = 3 – 3λ, из оторой находим µ = .
Теперь можно найти отношение QL : AL. Имеем
= = 1 – ,
и в силу равенства (*) получим = 1 – µ = . Отсюда =
= = ; та а S
QBC
= 1, то исомая площадь равна .
Ответ..
1
3
---
2
3
---
AM
2
3
---
a
AN
1
3
---
b
AL
2
3
---
a
1
3
---
b
AQ AL
AQ AL
µ
3
---
a b
CK
2
3
---
CA
1
3
---
CB
1
3
---
a b
CQ CK
λ
3
---
a b
AQ AC CQ
µ
3
---
a b b
λ
3
---
a b
a b
3
7
---
QL
AL
--------
AL AQ–
AL
----------------------- -
AQ
AL
-------- -
QL
AL
--------
4
7
---
S
ABC
S
QBC
------------------ -
1
1 µ–
-------------
7
4
---
7
4
---
7
4
---
§ 80. Решение геометрических задач методами векторной алгебры 483
17. В треуольние ABC, площадь отороо равна 6, на сто-
роне AB взята точа K, делящая эту сторону в отношении
AK : BK = 2 : 3, а на стороне AC — точа L, делящая AC в отноше-
нии AL : LC = 5 : 3. Точа Q пересечения прямых CK и BL отсто-
ит от прямой AB на расстояние 1,5. Найдите длину стороны AB.
18. Дан треуольни ABC. На сторонах AB и BC взяты точ-
и M и N соответственно та, что AB = 5AM, BC = 3BN. Отрез-
и AN и CM пересеаются в точе O. Найдите отношение пло-
щадей треуольниов AOC и ABC.
19. Точа K делит медиану AD треуольниа ABC в отноше-
нии 3 : 1, считая от вершины. В аом отношении прямая BK
делит площадь треуольниа ABC?
20. На аждой медиане треуольниа взята точа, делящая
медиану в отношении 1 : 3, считая от вершины. Найдите отно-
шение площади треуольниа с вершинами в этих точах пло-
щади исходноо треуольниа.
Решение неоторых задач основано на использовании вето-
ра , оллинеарноо биссетрисе ула между веторами и .
При этом бывает удобно представить ветор в следующем виде:
= + . (3)
21. В треуольние ABC даны стороны a, b, c. Найдите ,
де AA
1
— биссетриса внутреннео ула A треуольниа.
22. В треуольние ABC медиана BD пересеается с биссе-
трисой AF в точе O. Отношение площади треуольниа DOA
площади треуольниа BOF равно . Найдите AC : AB.
23. В треуольние ABC биссетриса AD делит сторону BC
в отношении BD : CD = 2 : 1. В аом отношении медиана CE
делит эту биссетрису?
24. Биссетрисы AD и BE треуольниа ABC пересеаются
в точе O. Найдите отношение площади треуольниа ABC пло-
щади четырехуольниа ODCE, если BC = a, AC = b, AB = c.
Решение неоторых задач основано на использовании сле-
дующео веторноо соотношения
: если A, B, C, D— четыре
точи, принадлежащие одной плосости, а O — произвольная
точа пространства, то
= α + β + (1 – α – β), (4)
де α Ý R, β Ý R.
c
a b
c
c
a
a
------
b
b
-----
AA
1
3
8
---
OD OA OB OC
484 Г л а в а 14. Метод координат и элементы векторной алгебры
25. Дан параллелепипед ABCDA
1
B
1
C
1
D
1
. Плосость пере-
сеает прямые AB, AD, AA
1
, AC
1
соответственно в точах B
0
,
D
0
, A
0
, C
0
. Доажите, что если = λ
1
, = λ
2
,
= λ
3
, = λ
4
, то
= + + .
26. Точи K, L, M, N взяты соответственно на сторонах
OA
1
, A
1
A
2
, A
2
A
3
, A
3
O неплосоо четырехуольниа OA
1
A
2
A
3
,
причем
= α , = β , = γ , = δ .
Доажите, что для принадлежности четырех точе K, L, M и N
одной плосости необходимо и достаточно выполнение равенст-
ва αβγδ = 1.
27. Даны два треуольниа A
1
A
2
A
3
и A
4
A
5
A
6
, не лежащие
в одной плосости. Доажите, что если M, N, P, Q, R и S— се-
редины отрезов A
1
A
2
, A
4
A
5
, A
2
A
3
, A
5
A
6
, A
3
A
4
, A
6
A
1
соответствен-
но, то веторы , и омпланарны.
28. Даны два треуольниа ABC и A
1
B
1
C
1
, не лежащие в од-
ной плосости: M и N— середины сторон AC и BC, а M
1
и
N
1
— середины сторон A
1
C
1
и B
1
C
1
. Доажите, что если =
= , то веторы , и омпланарны.
29. Даны две срещивающиеся прямые m и n. На прямой m
взяты точи P, Q, R, а на прямой n — точи P
1
, Q
1
, R
1
, причем
= k , = k . Доажите, что прямые PP
1
, QQ
1
,
RR
1
параллельны одной плосости.
При решении задач, связанных с отношением объемов час-
тей тетраэдра, образующихся при сечении ео неоторой пло-
состью, часто используют следующее утверждение
: если объем
тетраэдра ABCD равен V и на ео ребрах DA, DB, DC взяты
соответственно точи M, N, P та, что
DM = k
1
DA, DN = k
2
DB, DP = k
3
DC,
то объем тетраэдра MNPD равен k
1
k
2
k
3
V.
AC
0
AC
1
AB
0
AB
1
AD
0
AD
1
AA
0
AA
1
1
λ
1
----- -
1
λ
2
----- -
1
λ
3
----- -
1
λ
4
----- -
OK KA A
1
L LA
2
A
2
M MA
3
A
3
N NO
MN PQ RS
AB
A
1
B
1
MM
1
NN
1
CC
1
PQ PR P
1
Q
1
P
1
R
1
§ 80. Решение геометрических задач методами векторной алгебры 485
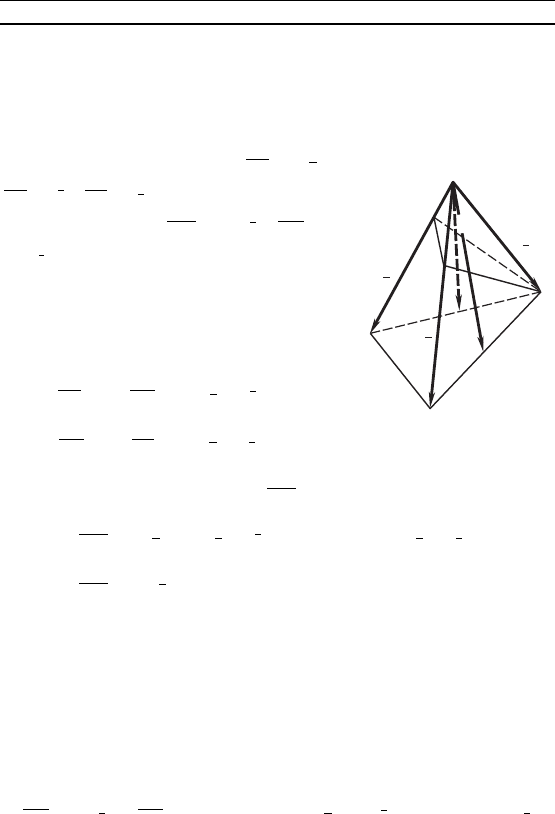
П р и м е р 6. Плосость проходит через вершину A основа-
ния треуольной пирамиды SABC и делит пополам медиану SK
треуольниа SAB, а медиану SL треуольниа SAC пересеает
в таой точе D, что 2SD = DL. В аом отношении эта пло-
сость делит объем пирамиды?
Р е ш е н и е. Положим = ,
= , = (рис. 71). Очевидно,
что k
1
= 1. Пусть = k
2
, =
= k
3
, де M и N— точи, в оторых
плосость сечения пересеается с реб-
рами SB и SC соответственно. Най-
дем k
2
и k
3
. Для этоо воспользуемся
равенствами
= = ( + ),
= = ( + ).
Соласно формуле (4), ветор можно представить в виде
= α + ( + ) + (1 – α – β)( + ).
Та а = k
2
, то, используя единственность разложения
ветора по трем неомпланарным веторам, получим систему
уравнений
0 = α + β + , k
2
= β,0 = (1 – α – β),
из оторой находим k
2
= .
Аналоично из равенств
= k
3
, = (α + + ) + + (1 – α – β)
находим k
3
= .
В силу сформулированноо ранее утверждения получаем
V
SAMN
= 1 · · V
SABC
,
M
N
K
L
b
A
C
S
B
c
a
E
D
Рис. 71
SA
a
SB b SC c
SM b SN
c
SE
1
2
---
SK
1
4
---
a b
SD
1
3
---
SL
1
6
---
a c
SM
SM a
β
4
---
a b
1
6
---
a c
SM b
5
6
---
1
12
------
1
6
---
1
4
---
1
6
---
1
3
---
SN c SN
5
6
---
β
12
------
1
6
---
a
β
4
---
b
1
6
---
c
1
5
---
1
3
---
1
5
---
484 Г л а в а 14. Метод координат и элементы векторной алгебры
25. Дан параллелепипед ABCDA
1
B
1
C
1
D
1
. Плосость пере-
сеает прямые AB, AD, AA
1
, AC
1
соответственно в точах B
0
,
D
0
, A
0
, C
0
. Доажите, что если = λ
1
, = λ
2
,
= λ
3
, = λ
4
, то
= + + .
26. Точи K, L, M, N взяты соответственно на сторонах
OA
1
, A
1
A
2
, A
2
A
3
, A
3
O неплосоо четырехуольниа OA
1
A
2
A
3
,
причем
= α , = β , = γ , = δ .
Доажите, что для принадлежности четырех точе K, L, M и N
одной плосости необходимо и достаточно выполнение равенст-
ва αβγδ = 1.
27. Даны два треуольниа A
1
A
2
A
3
и A
4
A
5
A
6
, не лежащие
в одной плосости. Доажите, что если M, N, P, Q, R и S— се-
редины отрезов A
1
A
2
, A
4
A
5
, A
2
A
3
, A
5
A
6
, A
3
A
4
, A
6
A
1
соответствен-
но, то веторы , и омпланарны.
28. Даны два треуольниа ABC и A
1
B
1
C
1
, не лежащие в од-
ной плосости: M и N— середины сторон AC и BC, а M
1
и
N
1
— середины сторон A
1
C
1
и B
1
C
1
. Доажите, что если =
= , то веторы , и омпланарны.
29. Даны две срещивающиеся прямые m и n. На прямой m
взяты точи P, Q, R, а на прямой n — точи P
1
, Q
1
, R
1
, причем
= k , = k . Доажите, что прямые PP
1
, QQ
1
,
RR
1
параллельны одной плосости.
При решении задач, связанных с отношением объемов час-
тей тетраэдра, образующихся при сечении ео неоторой пло-
состью, часто используют следующее утверждение
: если объем
тетраэдра ABCD равен V и на ео ребрах DA, DB, DC взяты
соответственно точи M, N, P та, что
DM = k
1
DA, DN = k
2
DB, DP = k
3
DC,
то объем тетраэдра MNPD равен k
1
k
2
k
3
V.
AC
0
AC
1
AB
0
AB
1
AD
0
AD
1
AA
0
AA
1
1
λ
1
----- -
1
λ
2
----- -
1
λ
3
----- -
1
λ
4
----- -
OK KA A
1
L LA
2
A
2
M MA
3
A
3
N NO
MN PQ RS
AB
A
1
B
1
MM
1
NN
1
CC
1
PQ PR P
1
Q
1
P
1
R
1
§ 80. Решение геометрических задач методами векторной алгебры 485
П р и м е р 6. Плосость проходит через вершину A основа-
ния треуольной пирамиды SABC и делит пополам медиану SK
треуольниа SAB, а медиану SL треуольниа SAC пересеает
в таой точе D, что 2SD = DL. В аом отношении эта пло-
сость делит объем пирамиды?
Р е ш е н и е. Положим = ,
= , = (рис. 71). Очевидно,
что k
1
= 1. Пусть = k
2
, =
= k
3
, де M и N— точи, в оторых
плосость сечения пересеается с реб-
рами SB и SC соответственно. Най-
дем k
2
и k
3
. Для этоо воспользуемся
равенствами
= = ( + ),
= = ( + ).
Соласно формуле (4), ветор можно представить в виде
= α + ( + ) + (1 – α – β)( + ).
Та а = k
2
, то, используя единственность разложения
ветора по трем неомпланарным веторам, получим систему
уравнений
0 = α + β + , k
2
= β,0 = (1 – α – β),
из оторой находим k
2
= .
Аналоично из равенств
= k
3
, = (α + + ) + + (1 – α – β)
находим k
3
= .
В силу сформулированноо ранее утверждения получаем
V
SAMN
= 1 · · V
SABC
,
M
N
K
L
b
A
C
S
B
c
a
E
D
Рис. 71
SA
a
SB b SC c
SM b SN
c
SE
1
2
---
SK
1
4
---
a b
SD
1
3
---
SL
1
6
---
a c
SM
SM a
β
4
---
a b
1
6
---
a c
SM b
5
6
---
1
12
------
1
6
---
1
4
---
1
6
---
1
3
---
SN c SN
5
6
---
β
12
------
1
6
---
a
β
4
---
b
1
6
---
c
1
5
---
1
3
---
1
5
---

486 Г л а в а 14. Метод координат и элементы векторной алгебры
и, следовательно, объем оставшейся части пирамиды равен
V
SABC
. Ита, исомое отношение объемов равно 1 : 14.
Ответ.1 : 14.
30. В трехранном уле с вершиной S проведены параллель-
ные сечения ABC и A
1
B
1
C
1
. Пусть V, V
1
, V
2
, V
3
— объемы тетра-
эдров SABC, SA
1
B
1
C
1
, SA
1
BC, SAB
1
C
1
соответственно. Поажи-
те, что V
2
= и V
2
V
3
= VV
1
.
31. Дана правильная четырехуольная пирамида SABCD.
Через середины ребер AB, AD и CS проведена плосость. В а-
ом отношении эта плосость делит объем пирамиды?
32. Объем пирамиды ABCD равен 5. Через середины ребер AD
и BC проведена плосость, пересеающая ребро CD в точе M.
При этом отношение длины отреза DM длине отреза MC
равно . Вычислите площадь сечения пирамиды уазанной
плосостью, если расстояние от нее до вершины A равно 1.
33. Плосость пересеает боовые ребра SA, SB и SC тре-
уольной пирамиды SABC в точах K, L и M соответственно.
В аом отношении эта плосость делит объем пирамиды, если
известно, что SK : KA = SL : LB = 2, а медиана SN треуольни-
а SBC делится этой плосостью пополам?
34. В треуольной пирамиде SABC все ребра равны. На реб-
ре SA взята точа M та, что SM = MA, а на ребре SB — точа
N та, что 3SN = SB. Через точи M и N проведена плосость,
параллельная медиане AD основания ABC. Найдите отношение
объема треуольной пирамиды, отсеаемой от исходной прове-
денной плосостью, объему пирамиды SABC.
§ 81. Задачи, решаемые с помощью
скалярного произведения векторов
Салярным произведением двух ненулевых веторов на-
зывают произведением длин этих веторов на осинус ула
между веторами:
· = | | · | | cos F(, ). (1)
14
15
------
V
2
V
1
3
2
3
---
a b a b a b
§ 81. Задачи, решаемые с помощью скалярного произведения 487
Необходимым и достаточным условием перпендиуляр-
ности двух ненулевых веторов является равенство нулю
их салярноо произведения:
· = 0. (2)
Если ϕ = F( , ), то
· > 0 при 0 m ϕ < ; · < 0 при < ϕ m π. (3)
Салярное произведение ветора на себя равно вадрату ео
длины:
· = = | |
2
.(4)
Свойства салярноо произведения
:
· = · (оммутативный заон);
(λ ) · = λ( · ) (ассоциативный заон);
· ( + ) = · + · (дистрибутивный заон).
П р и м е р 1. Известно, что веторы 3 – 5 и 2 + пер-
пендиулярны между собой и веторы + 4 и – + таже
взаимно перпендиулярны. Найти уол между веторами и .
Р е ш е н и е. По условию
(3 – 5 ) · (2 + ) = 0, ( + 4 ) · (– + ) = 0.
Отсюда следует, что
6
2
– 7 · – 5
2
= 0, –
2
– 3 · + 4
2
= 0, (*)
т. е. получили два уравнения относительно трех неизвестных
2
,
2
и . Соласно равенству (1), осинус ула между ве-
торами и вычисляется по формуле
cos F( , ) = . (**)
Из уравнений (*) находим
· =
2
,
2
=
2
. (***)
a
b
a b
a b
π
2
---
a b
π
2
---
a a a
2
a
a b b a
a b a b
a b c a b a c
a b a b
a b a b
a b
a b a b a b a b
a a b b a a b b
a b a b
a b
a b
ab⋅
ab⋅
----------------
a b
19
43
------
a b
25
43
------
a

486 Г л а в а 14. Метод координат и элементы векторной алгебры
и, следовательно, объем оставшейся части пирамиды равен
V
SABC
. Ита, исомое отношение объемов равно 1 : 14.
Ответ.1 : 14.
30. В трехранном уле с вершиной S проведены параллель-
ные сечения ABC и A
1
B
1
C
1
. Пусть V, V
1
, V
2
, V
3
— объемы тетра-
эдров SABC, SA
1
B
1
C
1
, SA
1
BC, SAB
1
C
1
соответственно. Поажи-
те, что V
2
= и V
2
V
3
= VV
1
.
31. Дана правильная четырехуольная пирамида SABCD.
Через середины ребер AB, AD и CS проведена плосость. В а-
ом отношении эта плосость делит объем пирамиды?
32. Объем пирамиды ABCD равен 5. Через середины ребер AD
и BC проведена плосость, пересеающая ребро CD в точе M.
При этом отношение длины отреза DM длине отреза MC
равно . Вычислите площадь сечения пирамиды уазанной
плосостью, если расстояние от нее до вершины A равно 1.
33. Плосость пересеает боовые ребра SA, SB и SC тре-
уольной пирамиды SABC в точах K, L и M соответственно.
В аом отношении эта плосость делит объем пирамиды, если
известно, что SK : KA = SL : LB = 2, а медиана SN треуольни-
а SBC делится этой плосостью пополам?
34. В треуольной пирамиде SABC все ребра равны. На реб-
ре SA взята точа M та, что SM = MA, а на ребре SB — точа
N та, что 3SN = SB. Через точи M и N проведена плосость,
параллельная медиане AD основания ABC. Найдите отношение
объема треуольной пирамиды, отсеаемой от исходной прове-
денной плосостью, объему пирамиды SABC.
§ 81. Задачи, решаемые с помощью
скалярного произведения векторов
Салярным произведением двух ненулевых веторов на-
зывают произведением длин этих веторов на осинус ула
между веторами:
· = | | · | | cos F(, ). (1)
14
15
------
V
2
V
1
3
2
3
---
a b a b a b
§ 81. Задачи, решаемые с помощью скалярного произведения 487
Необходимым и достаточным условием перпендиуляр-
ности двух ненулевых веторов является равенство нулю
их салярноо произведения:
· = 0. (2)
Если ϕ = F( , ), то
· > 0 при 0 m ϕ < ; · < 0 при < ϕ m π. (3)
Салярное произведение ветора на себя равно вадрату ео
длины:
· = = | |
2
.(4)
Свойства салярноо произведения
:
· = · (оммутативный заон);
(λ ) · = λ( · ) (ассоциативный заон);
· ( + ) = · + · (дистрибутивный заон).
П р и м е р 1. Известно, что веторы 3 – 5 и 2 + пер-
пендиулярны между собой и веторы + 4 и – + таже
взаимно перпендиулярны. Найти уол между веторами и .
Р е ш е н и е. По условию
(3 – 5 ) · (2 + ) = 0, ( + 4 ) · (– + ) = 0.
Отсюда следует, что
6
2
– 7 · – 5
2
= 0, –
2
– 3 · + 4
2
= 0, (*)
т. е. получили два уравнения относительно трех неизвестных
2
,
2
и . Соласно равенству (1), осинус ула между ве-
торами и вычисляется по формуле
cos F( , ) = . (**)
Из уравнений (*) находим
· =
2
,
2
=
2
. (***)
a
b
a b
a b
π
2
---
a b
π
2
---
a a a
2
a
a b b a
a b a b
a b c a b a c
a b a b
a b a b
a b
a b a b a b a b
a a b b a a b b
a b a b
a b
a b
ab⋅
ab⋅
----------------
a b
19
43
------
a b
25
43
------
a
