Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.

458 Г л а в а 14. Метод координат и элементы векторной алгебры
§ 78. Решение геометрических задач
с помощью метода координат
Геометричесие задачи этоо парарафа решаются с по-
мощью введения прямоуольной деартовой системы оорди-
нат на плосости или в пространстве. Приведенные ниже зада-
чи можно решить и методами элементарной еометрии. Одна-
о, а правило, таие решения требуют использования
нетривиальных, исусственных приемов.
П р и м е р 1. В равнобедренном треуольние ABC (AB =
= BC = 8) точа E делит боовую сторону AB в отношении 3 : 1
(считая от вершины B). Вычислить уол между веторами
и , если | | = 12.
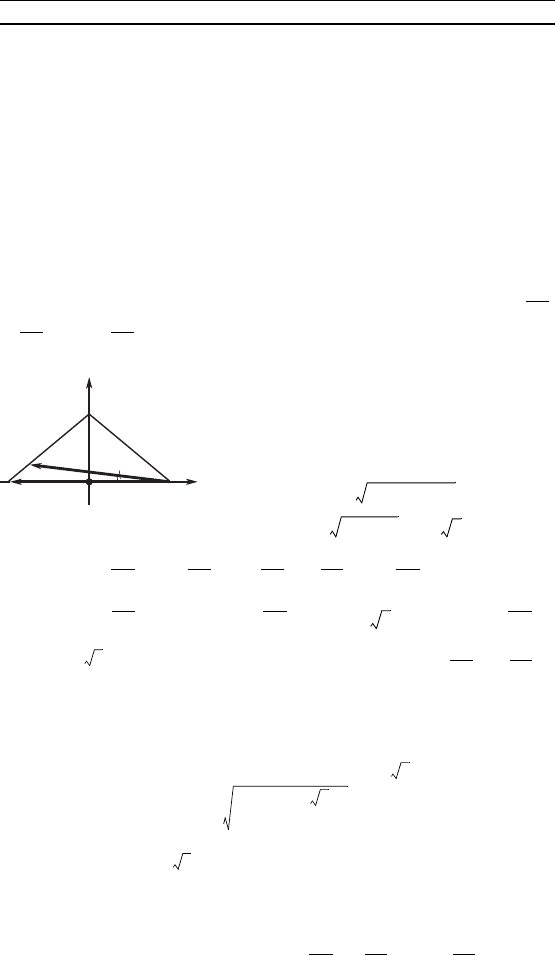
Решение. Введем систему оор-
динат xOy та, а уазано на рис. 58
(соласно свойству высоты равнобед-
ренноо треуольниа, OA = OC). Из
BOC находим
OB = =
= = 2 .
Та а = , то = + . Отсюда, учи-
тывая, что = {–12; 0}, = {6; 2 }, находим =
= – ; . Подставляя оординаты веторов и в
формулу салярноо произведения веторов, получаем
cos α = = .
Ответ. arccos .
1. В равнобедренном треуольние ABC (AB = BC = 15) точ-
а E делит сторону BC в отношении 1:4 (считая от вершины B).
Вычислите уол между веторами и , если = 20.
CE
CA CA
x
A
O
C
y
E
B
α
Рис. 58
BC
2
OC
2
–
8
2
6
2
– 7
AE
1
4
---
AB CE CA
1
4
---
AB
CA AB 7 CE
21
2
------
7
2
-------
CE
CA
12–()
21
2
------
–
⋅
12
21
2
------
2
7
2
-------
2
+
------------------------------------------------------ -
37
8
-----------
37
8
-----------
AE AC AC
§ 78. Решение геометрических задач с помощью метода координат 459
2. В прямоуольном треуольние ABC уол B— прямой,
AB = 3, BC = 4. Вычислите уол между медианами AM и BD.
3. В прямоуольном треуольние с атетами AB = 8 и
BC = 6 проведена прямая AD, делящая BC в отношении BD : DC =
= 4 : 5. Вычислите уол между веторами и .
4. В прямоуольном треуольние с атетами BC = 4 и BA =
=3 проведена прямая AD, делящая сторону BC в отношении
BD : DC = 3 : 5. Вычислите уол между веторами и .
5. Дан равнобедренный прямоуольный треуольни ABC
с прямым улом при вершине B; BS — ео высота, K— сере-
дина высоты BS, а M— точа пересечения прямой AK со сто-
роной BC. Найдите отношение, в отором точа M делит отре-
зо BC.
П р и м е р 2. Доазать, что если основания высот треуоль-
ниа ABC соединить отрезами прямых, то получится тре-
уольни, для отороо эти высоты будут биссетрисами.
Р е ш е н и е. Опустим из вершин треуольниа ео высоты:
AA
1
B BC, BB
1
B AC и CC
1
B AB; точу пересечения высот обо-
значим через O. Выберем систему оординат та, чтобы ее на-
чало
совпало
с
точой
C
1
,
а
ось
Ox
прошла
через
вершину
B
(рис. 59). Тода ось Oy пройдет че-
рез вершину C. Пусть оордина-
ты вершин треуольниа таовы:
A(–a; 0), B(b; 0), C(0; c). Доажем,
что высота C
1
C— биссетриса у-
ла A
1
C
1
B
1
.
Уравнение прямой, проходя-
щей через точи A и C, имеет вид
y = x + c,(*)
а уравнение прямой, проходящей
через точи B и O перпендиуляр-
но прямой AC,— вид
y = – x + (**)
(чтобы получить последнее уравнение, мы использовали со-
отношение k
1
k
2
= –1 между уловыми оэффициентами двух
взаимно перпендиулярных прямых). Решив систему уравне-
AB
AD
AD BC
x
A
B
C
y
O
A
1
B
1
C
1
Рис. 59
c
a
---
a
c
---
ab
c
------
458 Г л а в а 14. Метод координат и элементы векторной алгебры
§ 78. Решение геометрических задач
с помощью метода координат
Геометричесие задачи этоо парарафа решаются с по-
мощью введения прямоуольной деартовой системы оорди-
нат на плосости или в пространстве. Приведенные ниже зада-
чи можно решить и методами элементарной еометрии. Одна-
о, а правило, таие решения требуют использования
нетривиальных, исусственных приемов.
П р и м е р 1. В равнобедренном треуольние ABC (AB =
= BC = 8) точа E делит боовую сторону AB в отношении 3 : 1
(считая от вершины B). Вычислить уол между веторами
и , если | | = 12.
Решение. Введем систему оор-
динат xOy та, а уазано на рис. 58
(соласно свойству высоты равнобед-
ренноо треуольниа, OA = OC). Из
BOC находим
OB = =
= = 2 .
Та а = , то = + . Отсюда, учи-
тывая, что = {–12; 0}, = {6; 2 }, находим =
= – ; . Подставляя оординаты веторов и в
формулу салярноо произведения веторов, получаем
cos α = = .
Ответ. arccos .
1. В равнобедренном треуольние ABC (AB = BC = 15) точ-
а E делит сторону BC в отношении 1:4 (считая от вершины B).
Вычислите уол между веторами и , если = 20.
CE
CA CA
x
A
O
C
y
E
B
α
Рис. 58
BC
2
OC
2
–
8
2
6
2
– 7
AE
1
4
---
AB CE CA
1
4
---
AB
CA AB 7 CE
21
2
------
7
2
-------
CE
CA
12–()
21
2
------
–
⋅
12
21
2
------
2
7
2
-------
2
+
------------------------------------------------------ -
37
8
-----------
37
8
-----------
AE AC AC
§ 78. Решение геометрических задач с помощью метода координат 459
2. В прямоуольном треуольние ABC уол B— прямой,
AB = 3, BC = 4. Вычислите уол между медианами AM и BD.
3. В прямоуольном треуольние с атетами AB = 8 и
BC = 6 проведена прямая AD, делящая BC в отношении BD : DC =
= 4 : 5. Вычислите уол между веторами и .
4. В прямоуольном треуольние с атетами BC = 4 и BA =
=3 проведена прямая AD, делящая сторону BC в отношении
BD : DC = 3 : 5. Вычислите уол между веторами и .
5. Дан равнобедренный прямоуольный треуольни ABC
с прямым улом при вершине B; BS — ео высота, K— сере-
дина высоты BS, а M— точа пересечения прямой AK со сто-
роной BC. Найдите отношение, в отором точа M делит отре-
зо BC.
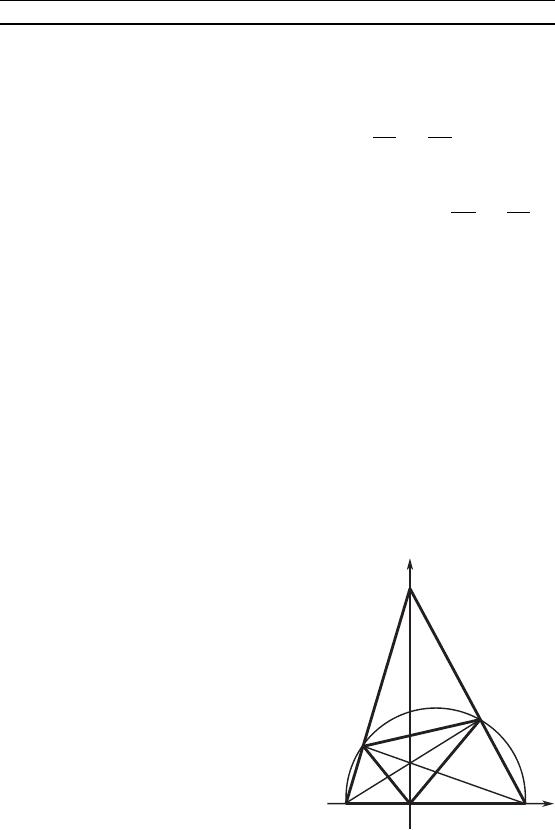
П р и м е р 2. Доазать, что если основания высот треуоль-
ниа ABC соединить отрезами прямых, то получится тре-
уольни, для отороо эти высоты будут биссетрисами.
Р е ш е н и е. Опустим из вершин треуольниа ео высоты:
AA
1
B BC, BB
1
B AC и CC
1
B AB; точу пересечения высот обо-
значим через O. Выберем систему оординат та, чтобы ее на-
чало
совпало
с
точой
C
1
,
а
ось
Ox
прошла
через
вершину
B
(рис. 59). Тода ось Oy пройдет че-
рез вершину C. Пусть оордина-
ты вершин треуольниа таовы:
A(–a; 0), B(b; 0), C(0; c). Доажем,
что высота C
1
C— биссетриса у-
ла A
1
C
1
B
1
.
Уравнение прямой, проходя-
щей через точи A и C, имеет вид
y = x + c,(*)
а уравнение прямой, проходящей
через точи B и O перпендиуляр-
но прямой AC,— вид
y = – x + (**)
(чтобы получить последнее уравнение, мы использовали со-
отношение k
1
k
2
= –1 между уловыми оэффициентами двух
взаимно перпендиулярных прямых). Решив систему уравне-
AB
AD
AD BC
x
A
B
C
y
O
A
1
B
1
C
1
Рис. 59
c
a
---
a
c
---
ab
c
------

460 Г л а в а 14. Метод координат и элементы векторной алгебры
ний (*) и (**), находим оординаты точи B
1
пересечения этих
прямых:
B
1
, .
Аналоично, составив уравнения прямых, проходящих
через пары точе B и C, A и O, получим оординаты точи A
1
:
A
1
, .
Записав уравнения прямых, проходящих через пары точе
A
1
и C
1
, B
1
и C
1
, находим уловые оэффициенты этих прямых:
= , = ,
отуда следует, что = – . Учитывая, что уловой о-
эффициент представляет собой таненс ула налона прямой
положительному направлению оси Ox, получаем
FBC
1
B
1
= π – FBC
1
A
1
,
отуда следует, что FAC
1
B
1
= FBC
1
A
1
. Та а прямая C
1
C
перпендиулярна прямой AB, то FB
1
C
1
C = FA
1
C
1
C, т. е. высо-
та C
1
C треуольниа ABC действительно является биссетри-
сой ула A
1
C
1
B
1
треуольниа A
1
B
1
C
1
.
Аналоично можно доазать, что и друие две высоты тре-
уольниа ABC являются биссетрисами соответствующих у-
лов треуольниа A
1
B
1
C
1
.
6. На высоте CC
1
треуольниа ABC дана произвольная точ-
а P. Прямые AP и BP пересеают стороны BC и CA соответ-
ственно в точах A
1
и B
1
. Доажите, что луч C
1
P является бис-
сетрисой ула A
1
C
1
B
1
.
7. Дан прямоуольный треуольни ABC с атетами a и b,
FC = 90°. Составьте уравнение множества точе M, для оторых
MA
2
+ MB
2
= 2MC
2
.
8. В плосости прямоуольниа ABCD дана точа M. Доа-
жите, что
MA
2
+ MC
2
= MB
2
+ MD
2
.
aab c
2
–()
a
2
c
2
+
--------------------------- -
ac a b+()
a
2
c
2
+
-------------------------
bc
2
ab–()
b
2
c
2
+
---------------------------
bc a b+()
b
2
c
2
+
------------------------ -
k
A
1
C
1
ca b+()
c
2
ab–
---------------------
k
B
1
C
1
ca b+()
ab c
2
–
---------------------
k
B
1
C
1
k
A
1
C
1
§ 78. Решение геометрических задач с помощью метода координат 461
19. Оружность вписана в ромб с улом 60°. Расстояние от
центра оружности до ближайшей вершины равно 1. Доажи-
те, что для любой точи P оружности выполняется равенство
PA
2
+ PB
2
+ PC
2
+ PD
2
= 11.
10. Доажите, что сумма вадратов расстояний от точи M,
взятой на диаметре неоторой оружности, до онцов любой из
параллельных этому диаметру хорд постоянна.
11. Ооло оружности описан вадрат ABCD. Из вершин
вадрата произвольной прямой, асающейся оружности, про-
ведены перпендиуляры AA
1
, BB
1
, CC
1
и DD
1
. Доажите, что
AA
1
· CC
1
= BB
1
· DD
1
.
12. Дан правильный треуольни ABC и оружность, ото-
рая проходит через вершины A и B, а ее центр D симметричен
вершине C относительно прямой AB. Доажите, что если M—
произвольная точа этой оружности, то из отрезов MA, MB,
MC можно составить прямоуольный треуольни.
13. В оружность вписан прямоуольни ABCD. Из произ-
вольной точи P оружности проведены перпендиуляры
прямым AB, BC, CD и DA, пересеающие эти прямые соот-
ветственно в точах K, L, M и N. Доажите, что точа N— орто-
центр треуольниа KLM (точа пересечения ео высот).
14. В вадрат вписана оружность. Доажите, что сумма
вадратов расстояний от точи оружности до вершин вадра-
та не зависит от выбора точи на оружности. Найдите эту
сумму.
15. Ооло вадрата описана оружность. Доажите, что
сумма вадратов расстояний от точи оружности до вершин
вадрата не зависит от выбора точи на оружности. Найдите
эту сумму.
Если в задаче рассматривается уб или прямоуольный па-
раллелепипед, то наиболее удобной является система оорди-
нат, начало оторой совпадает с одной из вершин нижнео ос-
нования этих тел, а оординатные оси проходят через ребра,
выходящие из уазанной вершины.
П р и м е р 3. Длина ребра уба ABCDA
1
B
1
C
1
D
1
равна 1. На
ребре AA
1
взята точа E та, что длина отреза AE равна , а
на ребре BC — точа F та, что длина отреза BF равна .
1
3
---
1
4
---

460 Г л а в а 14. Метод координат и элементы векторной алгебры
ний (*) и (**), находим оординаты точи B
1
пересечения этих
прямых:
B
1
, .
Аналоично, составив уравнения прямых, проходящих
через пары точе B и C, A и O, получим оординаты точи A
1
:
A
1
, .
Записав уравнения прямых, проходящих через пары точе
A
1
и C
1
, B
1
и C
1
, находим уловые оэффициенты этих прямых:
= , = ,
отуда следует, что = – . Учитывая, что уловой о-
эффициент представляет собой таненс ула налона прямой
положительному направлению оси Ox, получаем
FBC
1
B
1
= π – FBC
1
A
1
,
отуда следует, что FAC
1
B
1
= FBC
1
A
1
. Та а прямая C
1
C
перпендиулярна прямой AB, то FB
1
C
1
C = FA
1
C
1
C, т. е. высо-
та C
1
C треуольниа ABC действительно является биссетри-
сой ула A
1
C
1
B
1
треуольниа A
1
B
1
C
1
.
Аналоично можно доазать, что и друие две высоты тре-
уольниа ABC являются биссетрисами соответствующих у-
лов треуольниа A
1
B
1
C
1
.
6. На высоте CC
1
треуольниа ABC дана произвольная точ-
а P. Прямые AP и BP пересеают стороны BC и CA соответ-
ственно в точах A
1
и B
1
. Доажите, что луч C
1
P является бис-
сетрисой ула A
1
C
1
B
1
.
7. Дан прямоуольный треуольни ABC с атетами a и b,
FC = 90°. Составьте уравнение множества точе M, для оторых
MA
2
+ MB
2
= 2MC
2
.
8. В плосости прямоуольниа ABCD дана точа M. Доа-
жите, что
MA
2
+ MC
2
= MB
2
+ MD
2
.
aab c
2
–()
a
2
c
2
+
--------------------------- -
ac a b+()
a
2
c
2
+
-------------------------
bc
2
ab–()
b
2
c
2
+
---------------------------
bc a b+()
b
2
c
2
+
------------------------ -
k
A
1
C
1
ca b+()
c
2
ab–
---------------------
k
B
1
C
1
ca b+()
ab c
2
–
---------------------
k
B
1
C
1
k
A
1
C
1
§ 78. Решение геометрических задач с помощью метода координат 461
19. Оружность вписана в ромб с улом 60°. Расстояние от
центра оружности до ближайшей вершины равно 1. Доажи-
те, что для любой точи P оружности выполняется равенство
PA
2
+ PB
2
+ PC
2
+ PD
2
= 11.
10. Доажите, что сумма вадратов расстояний от точи M,
взятой на диаметре неоторой оружности, до онцов любой из
параллельных этому диаметру хорд постоянна.
11. Ооло оружности описан вадрат ABCD. Из вершин
вадрата произвольной прямой, асающейся оружности, про-
ведены перпендиуляры AA
1
, BB
1
, CC
1
и DD
1
. Доажите, что
AA
1
· CC
1
= BB
1
· DD
1
.
12. Дан правильный треуольни ABC и оружность, ото-
рая проходит через вершины A и B, а ее центр D симметричен
вершине C относительно прямой AB. Доажите, что если M—
произвольная точа этой оружности, то из отрезов MA, MB,
MC можно составить прямоуольный треуольни.
13. В оружность вписан прямоуольни ABCD. Из произ-
вольной точи P оружности проведены перпендиуляры
прямым AB, BC, CD и DA, пересеающие эти прямые соот-
ветственно в точах K, L, M и N. Доажите, что точа N— орто-
центр треуольниа KLM (точа пересечения ео высот).
14. В вадрат вписана оружность. Доажите, что сумма
вадратов расстояний от точи оружности до вершин вадра-
та не зависит от выбора точи на оружности. Найдите эту
сумму.
15. Ооло вадрата описана оружность. Доажите, что
сумма вадратов расстояний от точи оружности до вершин
вадрата не зависит от выбора точи на оружности. Найдите
эту сумму.
Если в задаче рассматривается уб или прямоуольный па-
раллелепипед, то наиболее удобной является система оорди-
нат, начало оторой совпадает с одной из вершин нижнео ос-
нования этих тел, а оординатные оси проходят через ребра,
выходящие из уазанной вершины.
П р и м е р 3. Длина ребра уба ABCDA
1
B
1
C
1
D
1
равна 1. На
ребре AA
1
взята точа E та, что длина отреза AE равна , а
на ребре BC — точа F та, что длина отреза BF равна .
1
3
---
1
4
---
462 Г л а в а 14. Метод координат и элементы векторной алгебры
Через центр уба O
1
и точи E и F проведена плосость. Найти
расстояние от вершины B
1
до этой плосости.
Р е ш е н и е. Выберем систему оординат та, чтобы ее на-
чало совпало с точой A, а оси Ox, Oy и Oz прошли через ребра
AB, AD и AA
1
соответственно. В этой системе оординат имеем
F 1; ; 0 , E 0; 0; , O
1
; ; .
Составим уравнение сеущей плосости. Пусть ветор =
={n
1
; n
2
; n
3
} перпендиулярен исомой плосости. Та а
веторы
= –1; – ; , = – ; ;
принадлежат этой плосости, то, используя условие перпенди-
улярности пар веторов и , и , запишем следую-
щую систему уравнений для n
1
, n
2
, n
3
:
Считая n
3
свободным неизвестным, находим n
1
= n
3
и n
2
=
=– n
3
. Полаая n
3
= 9, в ачестве ветора, перпендиулярно-
о исомой плосости, получаем ветор = {5; –8; 9}. Уравне-
ние плосости, проходящей через точу E 0; 0; перпенди-
улярно ветору = {5; –8; 9}, имеет вид
5x – 8y + 9z – 3 = 0. (*)
Координатами точи B
1
в выбранной системе оординат яв-
ляются (1; 0; 1). Вычислим расстояние от точи B
1
(1; 0; 1) до
плосости (*). Пусть M(x
0
; y
0
; z
0
) — точа основания перпен-
1
4
---
1
3
---
1
2
---
1
2
---
1
2
---
n
FE
1
4
---
1
3
---
FO
1
1
2
---
1
4
---
1
2
---
n
FE n FO
1
–n
1
– + = 0,
– + + = 0.
n
2
4
------
n
3
3
------
n
1
2
------
n
2
4
------
n
3
2
------
5
9
---
8
9
---
n
1
3
---
n
§ 78. Решение геометрических задач с помощью метода координат 463
диуляра данной плосости, проходящео через точу B
1
.
Та а точа M принадлежит плосости (*), то оординаты
этой точи должны удовлетворять уравнению плосости:
5x
0
– 8y
0
+ 9z
0
– 3 = 0. (**)
С друой стороны, ветор перпендиулярен данной плос-
ости, и, значит, этот ветор оллинеарен ветору :
= k .
Последнее равенство в оординатной форме дает следующие три
уравнения:
(***)
Решив систему уравнений (**) и (***), находим оординаты точ-
и M:
x
0
= , y
0
= – , z
0
=
и длину ветора | | = , оторая и является исомым
расстоянием от точи B
1
до плосости.
Ответ..
16. Длина ребра уба ABCDA
1
B
1
C
1
D
1
равна 1. На ребре BC
взята точа E та, что длина отреза BE равна , а на ребре
C
1
D
1
— точа F та, что длина отреза FD
1
равна . Через центр
уба и точи E и F проведена плосость. Найдите расстояние
от вершины A
1
до этой плосости.
17. Длина ребра уба ABCDA
1
B
1
C
1
D
1
равна 1. На ребре AB
взята точа E та, что длина отреза BE равна , а на ребре
CC
1
— точа F та, что длина отреза FC равна . Через центр
B
1
M
n
B
1
M n
x
0
– 1 = 5k,
y
0
= –8k,
z
0
– 1 = 9k.
115
170
----------
88
170
----------
71
170
----------
B
1
M
11
170
--------------
11
170
--------------
1
4
---
2
5
---
2
5
---
2
3
---

462 Г л а в а 14. Метод координат и элементы векторной алгебры
Через центр уба O
1
и точи E и F проведена плосость. Найти
расстояние от вершины B
1
до этой плосости.
Р е ш е н и е. Выберем систему оординат та, чтобы ее на-
чало совпало с точой A, а оси Ox, Oy и Oz прошли через ребра
AB, AD и AA
1
соответственно. В этой системе оординат имеем
F 1; ; 0 , E 0; 0; , O
1
; ; .
Составим уравнение сеущей плосости. Пусть ветор =
={n
1
; n
2
; n
3
} перпендиулярен исомой плосости. Та а
веторы
= –1; – ; , = – ; ;
принадлежат этой плосости, то, используя условие перпенди-
улярности пар веторов и , и , запишем следую-
щую систему уравнений для n
1
, n
2
, n
3
:
Считая n
3
свободным неизвестным, находим n
1
= n
3
и n
2
=
=– n
3
. Полаая n
3
= 9, в ачестве ветора, перпендиулярно-
о исомой плосости, получаем ветор = {5; –8; 9}. Уравне-
ние плосости, проходящей через точу E 0; 0; перпенди-
улярно ветору = {5; –8; 9}, имеет вид
5x – 8y + 9z – 3 = 0. (*)
Координатами точи B
1
в выбранной системе оординат яв-
ляются (1; 0; 1). Вычислим расстояние от точи B
1
(1; 0; 1) до
плосости (*). Пусть M(x
0
; y
0
; z
0
) — точа основания перпен-
1
4
---
1
3
---
1
2
---
1
2
---
1
2
---
n
FE
1
4
---
1
3
---
FO
1
1
2
---
1
4
---
1
2
---
n
FE n FO
1
–n
1
– + = 0,
– + + = 0.
n
2
4
------
n
3
3
------
n
1
2
------
n
2
4
------
n
3
2
------
5
9
---
8
9
---
n
1
3
---
n
§ 78. Решение геометрических задач с помощью метода координат 463
диуляра данной плосости, проходящео через точу B
1
.
Та а точа M принадлежит плосости (*), то оординаты
этой точи должны удовлетворять уравнению плосости:
5x
0
– 8y
0
+ 9z
0
– 3 = 0. (**)
С друой стороны, ветор перпендиулярен данной плос-
ости, и, значит, этот ветор оллинеарен ветору :
= k .
Последнее равенство в оординатной форме дает следующие три
уравнения:
(***)
Решив систему уравнений (**) и (***), находим оординаты точ-
и M:
x
0
= , y
0
= – , z
0
=
и длину ветора | | = , оторая и является исомым
расстоянием от точи B
1
до плосости.
Ответ..
16. Длина ребра уба ABCDA
1
B
1
C
1
D
1
равна 1. На ребре BC
взята точа E та, что длина отреза BE равна , а на ребре
C
1
D
1
— точа F та, что длина отреза FD
1
равна . Через центр
уба и точи E и F проведена плосость. Найдите расстояние
от вершины A
1
до этой плосости.
17. Длина ребра уба ABCDA
1
B
1
C
1
D
1
равна 1. На ребре AB
взята точа E та, что длина отреза BE равна , а на ребре
CC
1
— точа F та, что длина отреза FC равна . Через центр
B
1
M
n
B
1
M n
x
0
– 1 = 5k,
y
0
= –8k,
z
0
– 1 = 9k.
115
170
----------
88
170
----------
71
170
----------
B
1
M
11
170
--------------
11
170
--------------
1
4
---
2
5
---
2
5
---
2
3
---

464 Г л а в а 14. Метод координат и элементы векторной алгебры
уба и точи E и F проведена плосость α. Найдите расстояние
от вершины A до плосости α.
18. Длина ребра уба KLMNK
1
L
1
M
1
N
1
равна 1. На ребре
MM
1
взята точа A та, что длина отреза AM равна , а на
ребре K
1
N
1
— точа B та, что длина отреза K
1
B равна .
Через центр уба и точи A и B проведена плосость α. Точа
P— проеция вершины N на плосость α. Найдите длину от-
реза BP.
19. Длина ребра уба KLMNK
1
L
1
M
1
N
1
равна 1. На ребре KL
взята точа A та, что длина отреза AL равна , а на ребре
MM
1
— точа B та, что длина отреза MB равна . Через
центр уба и точи A и B проведена плосость. Найдите длину
отреза BP, де точа P— проеция вершины N на уазанную
плосость.
20. Длина ребра уба KLMNK
1
L
1
M
1
N
1
равна 1. На ребре KL
взята точа A та, что длина отреза KA равна , а на ребре
MM
1
— точа B та, что длина отреза M
1
B равна . Через
центр уба и точи A и B проведена плосость. Точа P— про-
еция вершины K
1
на эту плосость. Найдите длину отреза AP.
21. Дан уб ABCDA
1
B
1
C
1
D
1
; точа K— середина ребра AA
1
,
L— центр рани CC
1
D
1
D. Найдите уол между плосостями
BKL и AD
1
C.
22. Найдите площадь сечения уба ABCDA
1
B
1
C
1
D
1
плосо-
стью, проходящей через вершину A и середины ребер B
1
C
1
и D
1
C
1
.
Ребро уба равно a.
23. В убе ABCDA
1
B
1
C
1
D
1
с ребром a точа K— середина
ребра AB, точа L— середина ребра DD
1
. Найдите стороны
треуольниа A
1
KL и определите, в аом отношении делит
объем уба плосость, проходящая через вершины этоо тре-
уольниа.
24. В убе ABCDA
1
B
1
C
1
D
1
с ребром a середины ребер AA
1
,
A
1
B
1
, B
1
C
1
, C
1
C, CD, DA и AA
1
последовательно соединены. До-
3
5
---
1
3
---
3
4
---
3
5
---
1
4
---
2
5
---
§ 78. Решение геометрических задач с помощью метода координат 465
ажите, что полученная фиура есть правильный шестиуоль-
ни, и определите ео площадь.
25. Длина ребра уба ABCDA
1
B
1
C
1
D
1
равна a. Точи E и
F— середины ребер BC и B
1
C
1
соответственно. Рассматрива-
ются треуольнии, вершинами оторых служат точи пересе-
чения плосостей, параллельных основаниям уба, с прямыми
A
1
E, DF, AD
1
. Найдите:
а) площадь треуольниа, плосость отороо проходит че-
рез середину ребра AA
1
;
б) наименьшее возможное значение площади рассматривае-
мых треуольниов.
26. В уб вписана сфера. Доажите, что сумма вадратов
расстояний от точи сферы до вершин уба не зависит от выбо-
ра точи. Найдите эту сумму.
П р и м е р 4. Основанием пирамиды SABC является пра-
вильный треуольни ABC, длина стороны отороо равна 4 .
Боовое ребро SC перпендиулярно плосости основания и имеет
длину 2. Вычислить величину ула и расстояние между сре-
щивающимися прямыми, одна из оторых проходит через точ-
у S и середину ребра BC, а друая — через точу C и середину
ребра AB.
Р е ш е н и е. Введем прямоуольную систему оординат,
приняв за начало оординат точу C, за ось ординат — прямую
CD (точа D— середина AB), за ось апплиат — прямую CS, за
ось абсцисс — прямую, принадлежащую плосости треуольни-
а ABC и перпендиулярную прямой CD, а за единицу масшта-
ба — отрезо, длина отороо равна 1 (рис. 60). В этой системе
2
y
A
B
D
F
S
P
Q
C
z
x
E
Рис. 60

464 Г л а в а 14. Метод координат и элементы векторной алгебры
уба и точи E и F проведена плосость α. Найдите расстояние
от вершины A до плосости α.
18. Длина ребра уба KLMNK
1
L
1
M
1
N
1
равна 1. На ребре
MM
1
взята точа A та, что длина отреза AM равна , а на
ребре K
1
N
1
— точа B та, что длина отреза K
1
B равна .
Через центр уба и точи A и B проведена плосость α. Точа
P— проеция вершины N на плосость α. Найдите длину от-
реза BP.
19. Длина ребра уба KLMNK
1
L
1
M
1
N
1
равна 1. На ребре KL
взята точа A та, что длина отреза AL равна , а на ребре
MM
1
— точа B та, что длина отреза MB равна . Через
центр уба и точи A и B проведена плосость. Найдите длину
отреза BP, де точа P— проеция вершины N на уазанную
плосость.
20. Длина ребра уба KLMNK
1
L
1
M
1
N
1
равна 1. На ребре KL
взята точа A та, что длина отреза KA равна , а на ребре
MM
1
— точа B та, что длина отреза M
1
B равна . Через
центр уба и точи A и B проведена плосость. Точа P— про-
еция вершины K
1
на эту плосость. Найдите длину отреза AP.
21. Дан уб ABCDA
1
B
1
C
1
D
1
; точа K— середина ребра AA
1
,
L— центр рани CC
1
D
1
D. Найдите уол между плосостями
BKL и AD
1
C.
22. Найдите площадь сечения уба ABCDA
1
B
1
C
1
D
1
плосо-
стью, проходящей через вершину A и середины ребер B
1
C
1
и D
1
C
1
.
Ребро уба равно a.
23. В убе ABCDA
1
B
1
C
1
D
1
с ребром a точа K— середина
ребра AB, точа L— середина ребра DD
1
. Найдите стороны
треуольниа A
1
KL и определите, в аом отношении делит
объем уба плосость, проходящая через вершины этоо тре-
уольниа.
24. В убе ABCDA
1
B
1
C
1
D
1
с ребром a середины ребер AA
1
,
A
1
B
1
, B
1
C
1
, C
1
C, CD, DA и AA
1
последовательно соединены. До-
3
5
---
1
3
---
3
4
---
3
5
---
1
4
---
2
5
---
§ 78. Решение геометрических задач с помощью метода координат 465
ажите, что полученная фиура есть правильный шестиуоль-
ни, и определите ео площадь.
25. Длина ребра уба ABCDA
1
B
1
C
1
D
1
равна a. Точи E и
F— середины ребер BC и B
1
C
1
соответственно. Рассматрива-
ются треуольнии, вершинами оторых служат точи пересе-
чения плосостей, параллельных основаниям уба, с прямыми
A
1
E, DF, AD
1
. Найдите:
а) площадь треуольниа, плосость отороо проходит че-
рез середину ребра AA
1
;
б) наименьшее возможное значение площади рассматривае-
мых треуольниов.
26. В уб вписана сфера. Доажите, что сумма вадратов
расстояний от точи сферы до вершин уба не зависит от выбо-
ра точи. Найдите эту сумму.
П р и м е р 4. Основанием пирамиды SABC является пра-
вильный треуольни ABC, длина стороны отороо равна 4 .
Боовое ребро SC перпендиулярно плосости основания и имеет
длину 2. Вычислить величину ула и расстояние между сре-
щивающимися прямыми, одна из оторых проходит через точ-
у S и середину ребра BC, а друая — через точу C и середину
ребра AB.
Р е ш е н и е. Введем прямоуольную систему оординат,
приняв за начало оординат точу C, за ось ординат — прямую
CD (точа D— середина AB), за ось апплиат — прямую CS, за
ось абсцисс — прямую, принадлежащую плосости треуольни-
а ABC и перпендиулярную прямой CD, а за единицу масшта-
ба — отрезо, длина отороо равна 1 (рис. 60). В этой системе
2
y
A
B
D
F
S
P
Q
C
z
x
E
Рис. 60
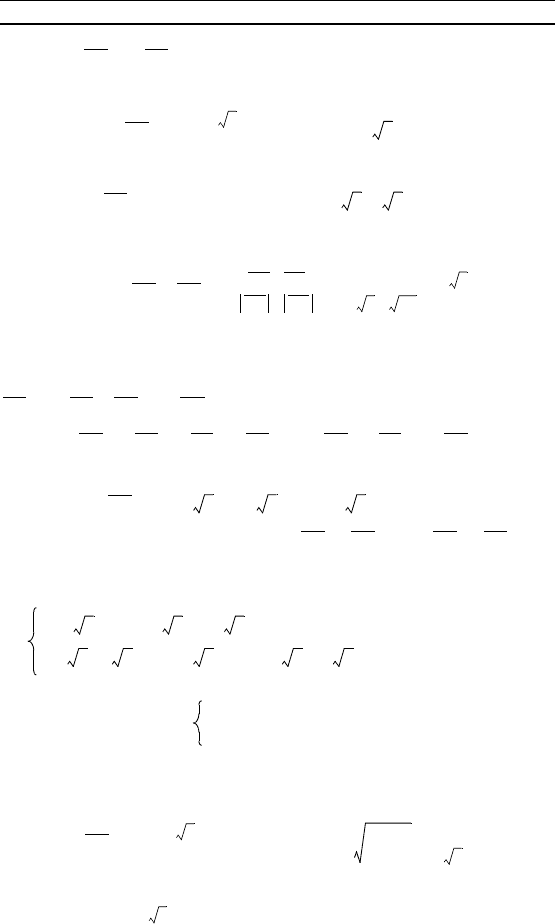
466 Г л а в а 14. Метод координат и элементы векторной алгебры
веторы и (точа E— середина стороны CB) имеют
следующие оординаты:
= 0; CB; 0 = {0; 2 ; 0},
= ; ; –CS = { ; ; –2}.
Поэтому
cos F(, ) = = = ,
и, значит, исомый уол равен 45°.
Пусть PQ — общий перпендиуляр прямым SE и CD
(P Ý SE, Q Ý CD). Тода существуют таие числа α и β, что
= α , = β . Ясно, что
= + + = –α – + β ,
или, в оординатной форме,
= {–α ; –α + β · 2 ; 2α – 2}.
Та а PQ B CD и PQ B SE, то · = 0, · = 0.
Последние два веторных уравнения в оординатной форме
имеют вид
или
отуда α = , β = . Ита,
= – ; 0; – , PQ = = .
Ответ.45°; .
27. Основанием пирамиды SABC является равнобедренный
прямоуольный треуольни ABC, длина ипотенузы AB ото-
CD
SE
CD
3
2
-------
6
SE
AB
4
--------
CD
2
-------- -
2 6
CD SE
CD SE⋅
CD SE⋅
----------------------------
12
26 12⋅
-------------------------- -
2
2
-------
SP SE CQ CD
PQ PS SC CQ SE CS CD
PQ 2 6 6
PQ CD PQ SE
(–α + β · 2 ) · 2 = 0,
–α · + (–α + β · 2 ) · + (2α – 2)(–2) = 0,
6 6 6
2 2 6 6 6
α = 2β,
–3α + 3β + 1 = 0,
2
3
---
1
3
---
PQ
22
3
-----------
2
3
---
8
9
---
4
9
---
+
2
3
-------
2
3
-------
§ 79. Простейшие задачи векторной алгебры 467
роо равна 4 . Боовое ребро пирамиды SC перпендиулярно
плосости основания, а ео длина равна 2. Найдите величи-
ну ула и расстояние между срещивающимися прямыми, од-
на из оторых проходит через точу S и середину ребра AC,
а друая — через точу C и середину ребра AB.
28. Основанием пирамиды HPQR является правильный тре-
уольни PQR, длина стороны отороо равна 2 . Боовое
ребро HR перпендиулярно плосости основания и имеет дли-
ну 1. Найдите величину ула и расстояние между срещиваю-
щимися прямыми, одна из оторых проходит через точу H
и середину ребра QR, а друая — через точу R и середину
ребра PQ.
29. Основанием пирамиды HPQR является равнобедренный
прямоуольный треуольни PQR, длина ипотенузы PQ о-
тороо равна 2 . Боовое ребро пирамиды перпендиулярно
плосости основания, а ео длина равна 1. Найдите величину
ула и расстояние между срещивающимися прямыми, одна из
оторых проходит через точу H и середину ребра PR, а дру-
ая — через точу R и середину ребра PQ.
30. Все ребра правильной призмы ABCA
1
B
1
C
1
имеют длину a.
Рассматриваются отрези, параллельные плосости ABB
1
A
1
и
таие, что их онцы лежат на диаоналях BC
1
и CA
1
боовых
раней.
а) Один из этих отрезов проведен через таую точу M
диаонали BC
1
, что BM:BC
1
= 1:3. Найдите ео длину.
б) Найдите наименьшую длину всех рассматриваемых от-
резов.
31. Сторона основания ABCD правильной пирамиды SABCD
имеет длину a, а боовое ребро — длину 2a. Рассматриваются
отрези, параллельные плосости рани SAD и таие, что их
онцы лежат на диаонали основания BD и боовом ребре SC.
Найдите наименьшую длину всех рассматриваемых отрезов.
§ 79. Простейшие задачи
векторной алгебры
Два ветора и считают равными, если:
1) длина ветора равна длине ветора ;
2) лучи и одинаово направлены.
2
2
2
AB CD
AB CD
AB CD

466 Г л а в а 14. Метод координат и элементы векторной алгебры
веторы и (точа E— середина стороны CB) имеют
следующие оординаты:
= 0; CB; 0 = {0; 2 ; 0},
= ; ; –CS = { ; ; –2}.
Поэтому
cos F(, ) = = = ,
и, значит, исомый уол равен 45°.
Пусть PQ — общий перпендиуляр прямым SE и CD
(P Ý SE, Q Ý CD). Тода существуют таие числа α и β, что
= α , = β . Ясно, что
= + + = –α – + β ,
или, в оординатной форме,
= {–α ; –α + β · 2 ; 2α – 2}.
Та а PQ B CD и PQ B SE, то · = 0, · = 0.
Последние два веторных уравнения в оординатной форме
имеют вид
или
отуда α = , β = . Ита,
= – ; 0; – , PQ = = .
Ответ.45°; .
27. Основанием пирамиды SABC является равнобедренный
прямоуольный треуольни ABC, длина ипотенузы AB ото-
CD
SE
CD
3
2
-------
6
SE
AB
4
--------
CD
2
-------- -
2 6
CD SE
CD SE⋅
CD SE⋅
----------------------------
12
26 12⋅
-------------------------- -
2
2
-------
SP SE CQ CD
PQ PS SC CQ SE CS CD
PQ 2 6 6
PQ CD PQ SE
(–α + β · 2 ) · 2 = 0,
–α · + (–α + β · 2 ) · + (2α – 2)(–2) = 0,
6 6 6
2 2 6 6 6
α = 2β,
–3α + 3β + 1 = 0,
2
3
---
1
3
---
PQ
22
3
-----------
2
3
---
8
9
---
4
9
---
+
2
3
-------
2
3
-------
§ 79. Простейшие задачи векторной алгебры 467
роо равна 4 . Боовое ребро пирамиды SC перпендиулярно
плосости основания, а ео длина равна 2. Найдите величи-
ну ула и расстояние между срещивающимися прямыми, од-
на из оторых проходит через точу S и середину ребра AC,
а друая — через точу C и середину ребра AB.
28. Основанием пирамиды HPQR является правильный тре-
уольни PQR, длина стороны отороо равна 2 . Боовое
ребро HR перпендиулярно плосости основания и имеет дли-
ну 1. Найдите величину ула и расстояние между срещиваю-
щимися прямыми, одна из оторых проходит через точу H
и середину ребра QR, а друая — через точу R и середину
ребра PQ.
29. Основанием пирамиды HPQR является равнобедренный
прямоуольный треуольни PQR, длина ипотенузы PQ о-
тороо равна 2 . Боовое ребро пирамиды перпендиулярно
плосости основания, а ео длина равна 1. Найдите величину
ула и расстояние между срещивающимися прямыми, одна из
оторых проходит через точу H и середину ребра PR, а дру-
ая — через точу R и середину ребра PQ.
30. Все ребра правильной призмы ABCA
1
B
1
C
1
имеют длину a.
Рассматриваются отрези, параллельные плосости ABB
1
A
1
и
таие, что их онцы лежат на диаоналях BC
1
и CA
1
боовых
раней.
а) Один из этих отрезов проведен через таую точу M
диаонали BC
1
, что BM:BC
1
= 1:3. Найдите ео длину.
б) Найдите наименьшую длину всех рассматриваемых от-
резов.
31. Сторона основания ABCD правильной пирамиды SABCD
имеет длину a, а боовое ребро — длину 2a. Рассматриваются
отрези, параллельные плосости рани SAD и таие, что их
онцы лежат на диаонали основания BD и боовом ребре SC.
Найдите наименьшую длину всех рассматриваемых отрезов.
§ 79. Простейшие задачи
векторной алгебры
Два ветора и считают равными, если:
1) длина ветора равна длине ветора ;
2) лучи и одинаово направлены.
2
2
2
AB CD
AB CD
AB CD
