Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.

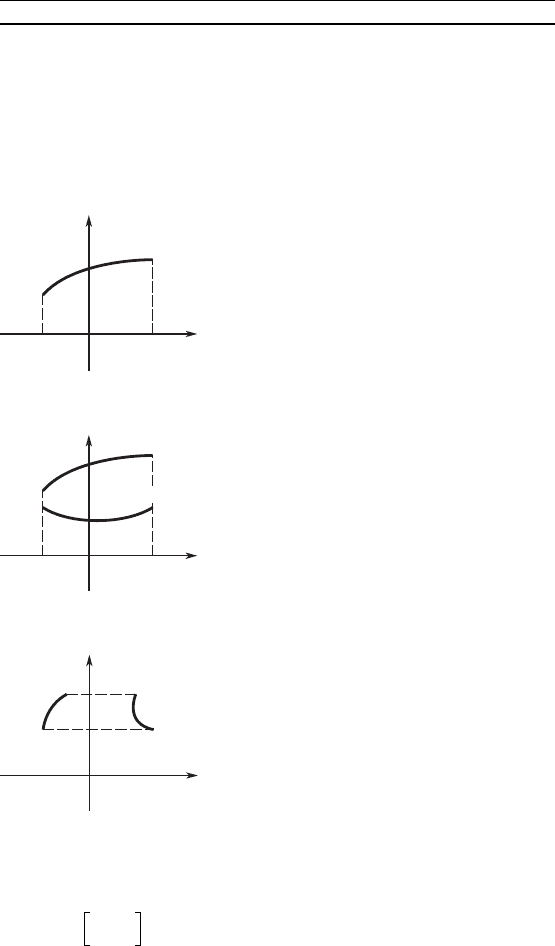
270 Г л а в а 10. Первообразная и интеграл
§ 57. Вычисление площадей фигур
Фиуру, ораниченную рафиом непрерывной фунции f(x)
(f(x) l 0), отрезами прямых x = a, x = b и осью Ox, называют
риволинейной трапецией (рис. 16). Ее площадь вычисляют
по формуле
S = f(x)dx.(1)
Если при всех x из промежута
[a; b] выполняется условие f
2
(x) l f
1
(x),
то площадь фиуры, ораниченной ра-
фиами непрерывных фунций y =
= f
1
(x), y = f
2
(x) и отрезами прямых
x = a, x = b (рис. 17), вычисляется по
формуле
S = (f
2
(x) – f
1
(x)) dx.(2)
Если при всех y из промежута
[c; d] выполняется условие ϕ
2
(y) l ϕ
1
(y),
то площадь фиуры, залюченной меж-
ду отрезами прямых y = c, y = d
и рафиами непрерывных фунций
x = ϕ
1
(y), x = ϕ
2
(y) (рис. 18), вычис-
ляется по формуле
S = (ϕ
2
(y) – ϕ
1
(y)) dy. (3)
П р и м е р 1. Найти площадь фи-
уры, ораниченной линиями x = 0,
x = , f
1
(x) = sin x, f
2
(x) = cos x.
Р е ш е н и е. Посольу зна разности f
2
(x) – f
1
(x) на про-
межуте 0; не остается постоянным, разобьем этот проме-
жуто на области, в оторых уазанная разность сохраняет
x
b
f(x)
a
y
O
x
b
y
2
= f
2
(x
)
a
y
O
y
1
= f
1
(x
)
x
c
x
2
= ϕ
2
(y)x
1
= ϕ
1
(y)
d
y
O
Рис. 18
Рис. 17
Рис. 16
a
b
∫
a
b
∫
c
d
∫
π
2
---
π
2
---
§ 57. Вычисление площадей фигур 271
зна. Для этоо составим уравнение f
2
(x) – f
1
(x) = 0, единствен-
ным орнем отороо, принадлежащим промежуту 0; ,
является точа x = . Та а sin x l cos x при x Ý ; и
sin x < cos x при x Ý 0; , то, используя формулу (2), получаем
S = (cos x – sin x)dx + (sin x – cos x)dx =
= (sin x + cos x) + (–cosx – sin x) =
= ( – 1) + (–1 + ) = 2( – 1).
Ответ. S = 2( – 1).
Заметим, что в силу симметрии фиуры относительно пря-
мой x = ее площадь можно было вычислить по формуле
S = 2 (cos x – sin x)dx.
Вычислите площадь фиуры, ораниченной уазанными
линиями:
1. y = x
2
+ x, y = x + 1.
2. y = –2x
2
+ 3x + 6, y = x + 2.
3. y = 0, y = 20 – 2x
2
– 6x.
4. y = x
2
, y = , y = 0, x = 2.
5. y = , x – 2y + 2 = 0, x = 2.
6. y = 4x – x
2
, y – x = 0.
7. y = , y = 6 – x.
8. y = x
3
, y = , x = 2.
9. y = x
2
+ 1, y = –x
2
+ 3.
π
2
---
π
4
---
π
4
---
π
2
---
π
4
---
0
π/4
∫
π/4
π/2
∫
0
π/4
π/4
π/2
2 2 2
2
π
4
---
0
π/4
∫
1
x
---
1
2
---
x
5
x
---
1
x
---
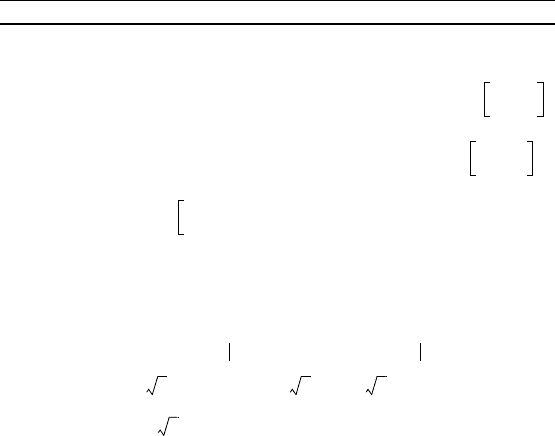
270 Г л а в а 10. Первообразная и интеграл
§ 57. Вычисление площадей фигур
Фиуру, ораниченную рафиом непрерывной фунции f(x)
(f(x) l 0), отрезами прямых x = a, x = b и осью Ox, называют
риволинейной трапецией (рис. 16). Ее площадь вычисляют
по формуле
S = f(x)dx.(1)
Если при всех x из промежута
[a; b] выполняется условие f
2
(x) l f
1
(x),
то площадь фиуры, ораниченной ра-
фиами непрерывных фунций y =
= f
1
(x), y = f
2
(x) и отрезами прямых
x = a, x = b (рис. 17), вычисляется по
формуле
S = (f
2
(x) – f
1
(x)) dx.(2)
Если при всех y из промежута
[c; d] выполняется условие ϕ
2
(y) l ϕ
1
(y),
то площадь фиуры, залюченной меж-
ду отрезами прямых y = c, y = d
и рафиами непрерывных фунций
x = ϕ
1
(y), x = ϕ
2
(y) (рис. 18), вычис-
ляется по формуле
S = (ϕ
2
(y) – ϕ
1
(y)) dy. (3)
П р и м е р 1. Найти площадь фи-
уры, ораниченной линиями x = 0,
x = , f
1
(x) = sin x, f
2
(x) = cos x.
Р е ш е н и е. Посольу зна разности f
2
(x) – f
1
(x) на про-
межуте 0; не остается постоянным, разобьем этот проме-
жуто на области, в оторых уазанная разность сохраняет
x
b
f(x)
a
y
O
x
b
y
2
= f
2
(x
)
a
y
O
y
1
= f
1
(x
)
x
c
x
2
= ϕ
2
(y)x
1
= ϕ
1
(y)
d
y
O
Рис. 18
Рис. 17
Рис. 16
a
b
∫
a
b
∫
c
d
∫
π
2
---
π
2
---
§ 57. Вычисление площадей фигур 271
зна. Для этоо составим уравнение f
2
(x) – f
1
(x) = 0, единствен-
ным орнем отороо, принадлежащим промежуту 0; ,
является точа x = . Та а sin x l cos x при x Ý ; и
sin x < cos x при x Ý 0; , то, используя формулу (2), получаем
S = (cos x – sin x)dx + (sin x – cos x)dx =
= (sin x + cos x) + (–cosx – sin x) =
= ( – 1) + (–1 + ) = 2( – 1).
Ответ. S = 2( – 1).
Заметим, что в силу симметрии фиуры относительно пря-
мой x = ее площадь можно было вычислить по формуле
S = 2 (cos x – sin x)dx.
Вычислите площадь фиуры, ораниченной уазанными
линиями:
1. y = x
2
+ x, y = x + 1.
2. y = –2x
2
+ 3x + 6, y = x + 2.
3. y = 0, y = 20 – 2x
2
– 6x.
4. y = x
2
, y = , y = 0, x = 2.
5. y = , x – 2y + 2 = 0, x = 2.
6. y = 4x – x
2
, y – x = 0.
7. y = , y = 6 – x.
8. y = x
3
, y = , x = 2.
9. y = x
2
+ 1, y = –x
2
+ 3.
π
2
---
π
4
---
π
4
---
π
2
---
π
4
---
0
π/4
∫
π/4
π/2
∫
0
π/4
π/4
π/2
2 2 2
2
π
4
---
0
π/4
∫
1
x
---
1
2
---
x
5
x
---
1
x
---

272 Г л а в а 10. Первообразная и интеграл
10. y = , y = 0, x = 0, x = .
11. y = 2
x
, y = 2, x = –1.
12. xy = 7, y = 0, x = 4, x = 12.
13. y = (x – 1)
2
, y = x + 1.
14. y = –x
2
+ 3,5x + 1, y = , x = 2 (x m 2).
15. x = 1, x = 2, y = 0, log
2
x + log
2
y = 0.
16. y = 2x
2
+ 1, y = x + 2, y = 1,5.
17. y = , y = , x = 1.
18. y = x
2
, y = 2 .
19. 2xy = 16 + x
2
, y = 5.
20. y = –1 + 8x
2
– x
4
, y = 15, x = 1 (x l 1).
21. y = , y = .
22. 3y = –x
2
+ 8x – 7, y + 1 = .
23. y = , y = , y = 0.
24. Найдите площадь фиуры, множество точе оторой удов-
летворяет системе неравенств
25. Вычислите площадь плосой фиуры, ораниченной час-
тями линий max {x; y} = 1 и x
2
+ y
2
= 1, лежащими в первой
оординатной четверти, де
max {x; y} =
26. Найдите площадь фиуры, ораниченной рафиами фун-
ций y = x
2
, y = 2x – x
2
.
Если фунция y = f(x) на промежуте [a; b] строо монотон-
на, то вычисление площади, ораниченной рафиом фунции
на этом промежуте и осью Ox, инода удобно свести вычис-
лению площади, ораниченной рафиом обратной фунции
x = g(y) на промежуте [c; d] и осью Oy, де
c = min {f(a); f(b)}, d = max {f(a); f(b)}.
1
cos
2
x
----------------
π
4
---
2
x–
2
x
4
x
2x
1
x
2
1+
---------------- -
x
2
2
------
4
x 3–
-------------
x 43x–
x
2
+ y
2
m r
2
, r > 0,
x – y m 0, y l 0.
x,еслиx l y,
y,еслиx < y.
§ 57. Вычисление площадей фигур 273
П р и м е р 2. Вычислить площадь
фиуры, ораниченной рафиом фун-
ции y = ln x, прямой x = 2 и осью Ox.
Р е ш е н и е. Фунцией, обратной
по отношению y = ln x, является
x = e
y
. Из рис. 19 видно, что площадь
заштрихованной фиуры S равна
разности площадей S
1
и S
2
, де S
1
—
прямоуольни со сторонами 2 и ln 2,
а S
2
— риволинейная трапеция OABC.
Соласно формуле (3), имеем
S
2
= e
y
dy = e
y
= e
ln 2
– e
0
= 2 – 1 = 1,
S
1
= 2 ln 2.
Таим образом, исомая площадь есть
S = S
1
– S
2
= 2 ln 2 – 1.
Ответ.2ln2 – 1.
Найдите площадь фиуры, ораниченной рафиами фун-
ций:
27. y = arcsin x, x = 1, y = 0.
28. y = arccos x, x = 0, y = 0.
Площади неоторых фиур лео вычисляются, если исполь-
зовать известные значения площадей частей руа радиуса R.
П р и м е р 3. Вычислить площадь фиуры, ораниченной
линиями y = , y = 0.
Р е ш е н и е. Возведя обе части равенства y =
в вадрат, получаем уравнение оружности единичноо радиуса:
y
2
+ x
2
= 1. Значит, рафи фунции y = представляет
собой верхнюю полуоружность радиуса 1. Ита, исомая пло-
щадь равна половине площади руа единичноо радиуса, т. е.
S = π · = .
Ответ..
x
CB
A
S
2
y
O 12
ln 2
S
Рис. 19
0
ln 2
∫
0
ln 2
1 x
2
–
1 x
2
–
1 x
2
–
1
2
---
1
2
π
2
---
π
2
---

272 Г л а в а 10. Первообразная и интеграл
10. y = , y = 0, x = 0, x = .
11. y = 2
x
, y = 2, x = –1.
12. xy = 7, y = 0, x = 4, x = 12.
13. y = (x – 1)
2
, y = x + 1.
14. y = –x
2
+ 3,5x + 1, y = , x = 2 (x m 2).
15. x = 1, x = 2, y = 0, log
2
x + log
2
y = 0.
16. y = 2x
2
+ 1, y = x + 2, y = 1,5.
17. y = , y = , x = 1.
18. y = x
2
, y = 2 .
19. 2xy = 16 + x
2
, y = 5.
20. y = –1 + 8x
2
– x
4
, y = 15, x = 1 (x l 1).
21. y = , y = .
22. 3y = –x
2
+ 8x – 7, y + 1 = .
23. y = , y = , y = 0.
24. Найдите площадь фиуры, множество точе оторой удов-
летворяет системе неравенств
25. Вычислите площадь плосой фиуры, ораниченной час-
тями линий max {x; y} = 1 и x
2
+ y
2
= 1, лежащими в первой
оординатной четверти, де
max {x; y} =
26. Найдите площадь фиуры, ораниченной рафиами фун-
ций y = x
2
, y = 2x – x
2
.
Если фунция y = f(x) на промежуте [a; b] строо монотон-
на, то вычисление площади, ораниченной рафиом фунции
на этом промежуте и осью Ox, инода удобно свести вычис-
лению площади, ораниченной рафиом обратной фунции
x = g(y) на промежуте [c; d] и осью Oy, де
c = min {f(a); f(b)}, d = max {f(a); f(b)}.
1
cos
2
x
----------------
π
4
---
2
x–
2
x
4
x
2x
1
x
2
1+
---------------- -
x
2
2
------
4
x 3–
-------------
x 43x–
x
2
+ y
2
m r
2
, r > 0,
x – y m 0, y l 0.
x,еслиx l y,
y,еслиx < y.
§ 57. Вычисление площадей фигур 273
П р и м е р 2. Вычислить площадь
фиуры, ораниченной рафиом фун-
ции y = ln x, прямой x = 2 и осью Ox.
Р е ш е н и е. Фунцией, обратной
по отношению y = ln x, является
x = e
y
. Из рис. 19 видно, что площадь
заштрихованной фиуры S равна
разности площадей S
1
и S
2
, де S
1
—
прямоуольни со сторонами 2 и ln 2,
а S
2
— риволинейная трапеция OABC.
Соласно формуле (3), имеем
S
2
= e
y
dy = e
y
= e
ln 2
– e
0
= 2 – 1 = 1,
S
1
= 2 ln 2.
Таим образом, исомая площадь есть
S = S
1
– S
2
= 2 ln 2 – 1.
Ответ.2ln2 – 1.
Найдите площадь фиуры, ораниченной рафиами фун-
ций:
27. y = arcsin x, x = 1, y = 0.
28. y = arccos x, x = 0, y = 0.
Площади неоторых фиур лео вычисляются, если исполь-
зовать известные значения площадей частей руа радиуса R.
П р и м е р 3. Вычислить площадь фиуры, ораниченной
линиями y = , y = 0.
Р е ш е н и е. Возведя обе части равенства y =
в вадрат, получаем уравнение оружности единичноо радиуса:
y
2
+ x
2
= 1. Значит, рафи фунции y = представляет
собой верхнюю полуоружность радиуса 1. Ита, исомая пло-
щадь равна половине площади руа единичноо радиуса, т. е.
S = π · = .
Ответ..
x
CB
A
S
2
y
O 12
ln 2
S
Рис. 19
0
ln 2
∫
0
ln 2
1 x
2
–
1 x
2
–
1 x
2
–
1
2
---
1
2
π
2
---
π
2
---

274 Г л а в а 10. Первообразная и интеграл
Найдите площадь фиуры, ораниченной линиями:
29. + = 1. 30. y
2
+ x
2
+ 2x = 0.
31. В деартовой системе оординат xOy фиура F ораниче-
на осью Ox, ривой y = 2x
2
и асательной этой ривой; абс-
цисса точи асания равна 2. Найдите площадь фиуры F.
32. Вычислите площадь фиуры, ораниченной параболой
y = x
2
– 2x + 2, асательной ней в точе M(3; 5) и осью орди-
нат. Сделайте рисуно.
33. Вычислите площадь фиуры, ораниченной линиями
y = + 1, x = 1 и асательной, проведенной в точе 2;
ривой y = + 1.
34. Найдите площадь фиуры, ораниченной линией y = x
2
–
–4x + 5 и прямыми, асающимися ее в точах с абсциссами
x
1
= 1 и x
2
= 4.
35. Из точи ; 0 параболе y = 2x
2
– 6x + 9 проведена
асательная, образующая острый уол с положительным направ-
лением оси Ox. Определите площадь фиуры, залюченной между
параболой, осью Ox, осью Oy и этой асательной.
36. Каую часть площади вадрата отсеает парабола, про-
ходящая через две соседние вершины вадрата и асающаяся
середины одной из ео сторон?
37. Каую часть площади полуруа отсеает парабола, про-
ходящая через онцы диаметра полуруа и асающаяся о-
ружности в точе, равноудаленной от онцов диаметра?
38. Найдите площадь фиуры, ораниченной прямой y =
= –8x – 46 и параболой y = 4x
2
+ ax + 2, если известно, что а-
сательная параболе в точе x = –5 составляет с осью Ox уол
π – arctg 20.
39. При аом значении a площадь фиуры, ораниченной
линиями y = , y = , x = 2, x = a, равна ln ?
40. При аом значении a прямая y = a делит площадь
фиуры, ораниченной линиями y = 0, y = 2 + x – x
2
, по-
полам?
x
2
a
2
------
y
2
b
2
----- -
1
x
---
3
2
---
1
x
---
3
2
---
1
x
---
1
2x 1–
-----------------
4
5
-------
§ 58. Задачи на отыскание наибольших (наименьших) площадей 275
41. При аом значении параметра a (a > 0) площадь фиуры,
ораниченной ривыми y = a , y = и осью Oy, равна
числу b? При аих значениях b задача имеет решение?
42. При аом значении a площадь фиуры, ораниченной
ривой y = sin 2x, прямыми x = , x = a и осью Ox, равна ?
43. Найдите все значения параметра b (b > 0), при оторых
площадь фиуры, ораниченной ривыми y = 1 – x
2
и y = bx
2
,
равна a. При аих значениях a задача имеет решение?
44. Через точу (x
0
; y
0
) рафиа фунции y =
проведите нормаль этому рафиу, если известно, что прямая
x = x
0
делит площадь, ораниченную данной ривой, осью Ox
и прямыми x = 0 и x = , на равные части.
§ 58. Задачи на отыскание наибольших
(наименьших) площадей фигур
Если в задаче требуется найти положение ривых, завися-
щих от одноо или несольих параметров, при отором пло-
щадь фиуры, ораниченной этими ривыми, масимальна (ми-
нимальна), то сначала следует составить фунцию, выражаю-
щую зависимость этой площади от параметров, а затем решать
задачу на отысание наибольшео (наименьшео) значения этой
фунции в области возможноо изменения параметров.
П р и м е р 1. Найти все значения параметра a (a l 1), при
оторых площадь фиуры, ораниченной прямыми y = 1, y = 2
и ривыми y = ax
2
, y = ax
2
, является наибольшей.
Р е ш е н и е. Вычислим значение площади при фисиро-
ванном значении a. В данном случае удобно вычислять пло-
щадь, считая y независимой переменной. В силу симметрии
парабол y = ax
2
и y = ax
2
относительно оси Oy площадь фи-
уры, лежащей в полуплосости x > 0, равна площади фиу-
ры, лежащей в полуплосости x < 0. Поэтому исомая пло-
x
2 x–
π
6
---
1
2
---
1cos2x+
3π
4
------ -
1
2
---
1
2
---
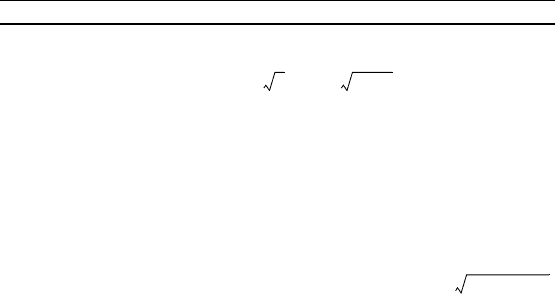
274 Г л а в а 10. Первообразная и интеграл
Найдите площадь фиуры, ораниченной линиями:
29. + = 1. 30. y
2
+ x
2
+ 2x = 0.
31. В деартовой системе оординат xOy фиура F ораниче-
на осью Ox, ривой y = 2x
2
и асательной этой ривой; абс-
цисса точи асания равна 2. Найдите площадь фиуры F.
32. Вычислите площадь фиуры, ораниченной параболой
y = x
2
– 2x + 2, асательной ней в точе M(3; 5) и осью орди-
нат. Сделайте рисуно.
33. Вычислите площадь фиуры, ораниченной линиями
y = + 1, x = 1 и асательной, проведенной в точе 2;
ривой y = + 1.
34. Найдите площадь фиуры, ораниченной линией y = x
2
–
–4x + 5 и прямыми, асающимися ее в точах с абсциссами
x
1
= 1 и x
2
= 4.
35. Из точи ; 0 параболе y = 2x
2
– 6x + 9 проведена
асательная, образующая острый уол с положительным направ-
лением оси Ox. Определите площадь фиуры, залюченной между
параболой, осью Ox, осью Oy и этой асательной.
36. Каую часть площади вадрата отсеает парабола, про-
ходящая через две соседние вершины вадрата и асающаяся
середины одной из ео сторон?
37. Каую часть площади полуруа отсеает парабола, про-
ходящая через онцы диаметра полуруа и асающаяся о-
ружности в точе, равноудаленной от онцов диаметра?
38. Найдите площадь фиуры, ораниченной прямой y =
= –8x – 46 и параболой y = 4x
2
+ ax + 2, если известно, что а-
сательная параболе в точе x = –5 составляет с осью Ox уол
π – arctg 20.
39. При аом значении a площадь фиуры, ораниченной
линиями y = , y = , x = 2, x = a, равна ln ?
40. При аом значении a прямая y = a делит площадь
фиуры, ораниченной линиями y = 0, y = 2 + x – x
2
, по-
полам?
x
2
a
2
------
y
2
b
2
----- -
1
x
---
3
2
---
1
x
---
3
2
---
1
x
---
1
2x 1–
-----------------
4
5
-------
§ 58. Задачи на отыскание наибольших (наименьших) площадей 275
41. При аом значении параметра a (a > 0) площадь фиуры,
ораниченной ривыми y = a , y = и осью Oy, равна
числу b? При аих значениях b задача имеет решение?
42. При аом значении a площадь фиуры, ораниченной
ривой y = sin 2x, прямыми x = , x = a и осью Ox, равна ?
43. Найдите все значения параметра b (b > 0), при оторых
площадь фиуры, ораниченной ривыми y = 1 – x
2
и y = bx
2
,
равна a. При аих значениях a задача имеет решение?
44. Через точу (x
0
; y
0
) рафиа фунции y =
проведите нормаль этому рафиу, если известно, что прямая
x = x
0
делит площадь, ораниченную данной ривой, осью Ox
и прямыми x = 0 и x = , на равные части.
§ 58. Задачи на отыскание наибольших
(наименьших) площадей фигур
Если в задаче требуется найти положение ривых, завися-
щих от одноо или несольих параметров, при отором пло-
щадь фиуры, ораниченной этими ривыми, масимальна (ми-
нимальна), то сначала следует составить фунцию, выражаю-
щую зависимость этой площади от параметров, а затем решать
задачу на отысание наибольшео (наименьшео) значения этой
фунции в области возможноо изменения параметров.
П р и м е р 1. Найти все значения параметра a (a l 1), при
оторых площадь фиуры, ораниченной прямыми y = 1, y = 2
и ривыми y = ax
2
, y = ax
2
, является наибольшей.
Р е ш е н и е. Вычислим значение площади при фисиро-
ванном значении a. В данном случае удобно вычислять пло-
щадь, считая y независимой переменной. В силу симметрии
парабол y = ax
2
и y = ax
2
относительно оси Oy площадь фи-
уры, лежащей в полуплосости x > 0, равна площади фиу-
ры, лежащей в полуплосости x < 0. Поэтому исомая пло-
x
2 x–
π
6
---
1
2
---
1cos2x+
3π
4
------ -
1
2
---
1
2
---
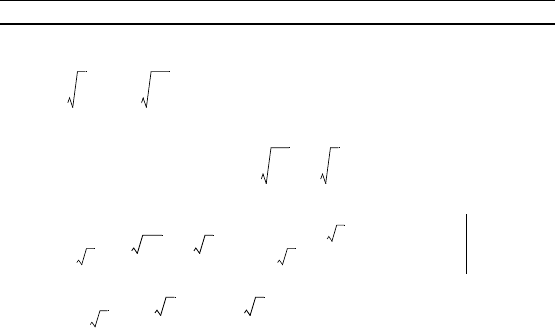
276 Г л а в а 10. Первообразная и интеграл
щадь равна удвоенной площади фиуры, ораниченной линия-
ми x = , x = , y = 1, y =2:
S(a) = 2 – dy =
= ( – ) dy = – y
3/2
=
= · ( – 1) (2 – 1), де a Ý [1; +×).
Очевидно, что фунция S(a) монотонно убывает на промежуте
[1; +×) и принимает наибольшее значение на левом онце это-
о промежута, т. е. при a = 1.
Ответ. a = 1.
1. При аом значении a площадь, ораниченная ривой
y = a
2
x
2
+ ax + 1 и прямыми y = 0, x = 1, является наимень-
шей?
2. Найдите все значения параметра a (a > 0), при оторых
площадь фиуры, ораниченной прямой y = и парабо-
лой y = , является наибольшей.
3. При аом положительном a площадь S риволинейной
трапеции, ораниченной линиями y = + , y = 0, x = a,
x =2a, принимает наименьшее значение?
4. Пусть S(k) — площадь, залюченная между параболой
y
1
= x
2
+ 2x – 3 и прямой y
2
= kx + 1. Найдите S(–1) и вычис-
лите наименьшее значение S(k).
П р и м е р 2. К параболе y = x
2
проведена асательная та,
что абсцисса x
0
точи асания принадлежит промежуту [1; 2].
Определить значение x
0
, при отором треуольни, ораничен-
ный асательной, осью ординат и прямой y = , имеет наи-
большую площадь.
y
a
---
2y
a
------ -
1
2
∫
2y
a
------ -
y
a
---
2
a
-------
1
2
∫
2y y
2
a
-------
22y
3/2
3
---------------------- -
2
3
---
1
2
2
a
-------
2
3
---
2 2
a
2
ax–
1 a
4
+
--------------------
x
2
2ax 3a
2
++
1 a
4
+
------------------------------------------
x
6
---
1
x
2
------
x
0
2
§ 58. Задачи на отыскание наибольших (наименьших) площадей 277
Р е ш е н и е. Для параболы y = x
2
уравнение асательной
в точе x
0
имеет вид y – = 2x
0
(x – x
0
). Ордината точи пере-
сечения асательной и оси Oy равна
y
1
= – 2 = – ,
а площадь исомоо прямоуольноо треуольниа вычисляет-
ся по формуле
S(x
0
) = = .
Требуется найти наибольшее значение S(x
0
) на промежуте
[1; 2]. Очевидно, что фунция S(x
0
) возрастает на этом проме-
жуте, и, следовательно, S(x
0
) = S(2) = 8.
Ответ. x
0
= 2.
5. К рафиу фунции y = проведена асательная
та, что абсцисса x
0
точи асания принадлежит промежуту
; 1 . При аом значении x
0
площадь S(x
0
) треуольниа,
ораниченноо этой асательной, осью Ox и прямой x = 2, яв-
ляется наименьшей и чему равна эта наименьшая площадь?
6. Криволинейная трапеция ораничена ривой y = x
2
+ 1 и
прямыми x = 1, x = 2. В аой точе данной ривой с абсцис-
сой x Ý [1; 2] следует провести асательную, чтобы она отсеа-
ла от риволинейной трапеции обычную трапецию наибольшей
площади?
7. При аом значении параметра a площадь фиуры, ора-
ниченной осью абсцисс, рафиом фунции y = x
3
+ 3x
2
+ x + a
и прямыми, параллельными оси ординат и пересеающими
ось абсцисс в точах эстремума этой фунции, является наи-
меньшей?
8. При аих значениях a из промежута [0; 1] площадь фи-
уры, ораниченной рафиом фунции y = f(x) и прямыми x = 0,
x = 1, y = f(a), является наибольшей, а при аих a — наимень-
шей, если f(x) = x
α
+ 3x
β
(α, β Ý R, причем α > 1, β > 1)?
9. При аих значениях a площадь фиуры, ораниченной
рафиом ривой – x
2
+ a, прямыми x = 0, x = 2 и осью Ox,
достиает минимума?
x
0
2
x
0
2
x
0
2
x
0
2
x
0
x
0
2
x
0
2
+()
2
-------------------------------
x
0
3
max
x
0
Ý [1; 2]
x
2
3
1
2
---
x
3
3
------

276 Г л а в а 10. Первообразная и интеграл
щадь равна удвоенной площади фиуры, ораниченной линия-
ми x = , x = , y = 1, y =2:
S(a) = 2 – dy =
= ( – ) dy = – y
3/2
=
= · ( – 1) (2 – 1), де a Ý [1; +×).
Очевидно, что фунция S(a) монотонно убывает на промежуте
[1; +×) и принимает наибольшее значение на левом онце это-
о промежута, т. е. при a = 1.
Ответ. a = 1.
1. При аом значении a площадь, ораниченная ривой
y = a
2
x
2
+ ax + 1 и прямыми y = 0, x = 1, является наимень-
шей?
2. Найдите все значения параметра a (a > 0), при оторых
площадь фиуры, ораниченной прямой y = и парабо-
лой y = , является наибольшей.
3. При аом положительном a площадь S риволинейной
трапеции, ораниченной линиями y = + , y = 0, x = a,
x =2a, принимает наименьшее значение?
4. Пусть S(k) — площадь, залюченная между параболой
y
1
= x
2
+ 2x – 3 и прямой y
2
= kx + 1. Найдите S(–1) и вычис-
лите наименьшее значение S(k).
П р и м е р 2. К параболе y = x
2
проведена асательная та,
что абсцисса x
0
точи асания принадлежит промежуту [1; 2].
Определить значение x
0
, при отором треуольни, ораничен-
ный асательной, осью ординат и прямой y = , имеет наи-
большую площадь.
y
a
---
2y
a
------ -
1
2
∫
2y
a
------ -
y
a
---
2
a
-------
1
2
∫
2y y
2
a
-------
22y
3/2
3
---------------------- -
2
3
---
1
2
2
a
-------
2
3
---
2 2
a
2
ax–
1 a
4
+
--------------------
x
2
2ax 3a
2
++
1 a
4
+
------------------------------------------
x
6
---
1
x
2
------
x
0
2
§ 58. Задачи на отыскание наибольших (наименьших) площадей 277
Р е ш е н и е. Для параболы y = x
2
уравнение асательной
в точе x
0
имеет вид y – = 2x
0
(x – x
0
). Ордината точи пере-
сечения асательной и оси Oy равна
y
1
= – 2 = – ,
а площадь исомоо прямоуольноо треуольниа вычисляет-
ся по формуле
S(x
0
) = = .
Требуется найти наибольшее значение S(x
0
) на промежуте
[1; 2]. Очевидно, что фунция S(x
0
) возрастает на этом проме-
жуте, и, следовательно, S(x
0
) = S(2) = 8.
Ответ. x
0
= 2.
5. К рафиу фунции y = проведена асательная
та, что абсцисса x
0
точи асания принадлежит промежуту
; 1 . При аом значении x
0
площадь S(x
0
) треуольниа,
ораниченноо этой асательной, осью Ox и прямой x = 2, яв-
ляется наименьшей и чему равна эта наименьшая площадь?
6. Криволинейная трапеция ораничена ривой y = x
2
+ 1 и
прямыми x = 1, x = 2. В аой точе данной ривой с абсцис-
сой x Ý [1; 2] следует провести асательную, чтобы она отсеа-
ла от риволинейной трапеции обычную трапецию наибольшей
площади?
7. При аом значении параметра a площадь фиуры, ора-
ниченной осью абсцисс, рафиом фунции y = x
3
+ 3x
2
+ x + a
и прямыми, параллельными оси ординат и пересеающими
ось абсцисс в точах эстремума этой фунции, является наи-
меньшей?
8. При аих значениях a из промежута [0; 1] площадь фи-
уры, ораниченной рафиом фунции y = f(x) и прямыми x = 0,
x = 1, y = f(a), является наибольшей, а при аих a — наимень-
шей, если f(x) = x
α
+ 3x
β
(α, β Ý R, причем α > 1, β > 1)?
9. При аих значениях a площадь фиуры, ораниченной
рафиом ривой – x
2
+ a, прямыми x = 0, x = 2 и осью Ox,
достиает минимума?
x
0
2
x
0
2
x
0
2
x
0
2
x
0
x
0
2
x
0
2
+()
2
-------------------------------
x
0
3
max
x
0
Ý [1; 2]
x
2
3
1
2
---
x
3
3
------

278 Г л а в а 10. Первообразная и интеграл
10. При аих значениях a из промежута [0; 1] площадь
фиуры, ораниченной рафиом фунции f(x) и прямыми x = 0,
x = 1, y = f(a), является наибольшей, а при аих a— наи-
меньшей, если f(x) = ?
11. При аих значениях a площадь фиуры, ораниченной
прямыми x = x
1
, x = x
2
, рафиом фунции y = | sin x + cos x – a |
и осью абсцисс, де x
1
и x
2
— два последовательных эстрему-
ма фунции f(x) = sin x + , является наименьшей?
§ 59. Вычисление объемов тел
Объем V тела, полученноо при вращении вору оси Ox ри-
волинейной трапеции, ораниченной линиями y = f(x) (f(x) l 0),
x = a, x = b (b > a), вычисляется по формуле
V = π f
2
(x)dx.(1)
Объем V тела, образованноо при вращении вору оси Oy
риволинейной трапеции, ораниченной линиями x = ϕ(y)
(ϕ (y) l 0), y = c, y = d (d > c) и осью Oy, вычисляется по фор-
муле
V = πϕ
2
(y)dy.(2)
П р и м е р. Вычислить объем тела, образованноо вращени-
ем одной ари синусоиды (рафиа фунции y = sin x на про-
межуте [0; π]) вору оси Ox.
Р е ш е н и е. По формуле (1) находим
V = π sin
2
x dx = π dx =
= π x + sin 2x = .
Ответ..
1 x
2
–
2
π
4
---
a
b
∫
c
d
∫
0
π
∫
0
π
∫
1cos2x–
2
---------------------------
1
2
---
1
4
---
0
π
π
2
2
----- -
π
2
2
----- -
§ 60. Приложения опред. интеграла к задачам физики 279
1. Вычислите объем тела, образованноо вращением вору
оси абсцисс риволинейной трапеции, ораниченной ипербо-
лой xy = 2, прямыми x = 1, x = 2 и осью абсцисс.
2. Вычислите объем тела, образованноо вращением вору
оси абсцисс фиуры, ораниченной параболами y
2
= x, y = x
2
.
3. Цепная линия y = вращается вору оси абсцисс.
При этом получается поверхность, называемая атеноидом.
Вычислите объем тела, образованноо атеноидом и двумя
плосостями, перпендиулярными оси абсцисс и отстоящими
от начала оординат на расстояния a и b.
4. Вычислите объем тела, полученноо вращением вору
оси ординат фиуры, ораниченной параболой y = 2x – x
2
и
осью абсцисс.
5. Найдите объем тела, полученноо вращением вору
оси Oy риволинейной трапеции, ораниченной линиями
y = arcsin x, y = и x = 0.
6. Найдите объем тела, полученноо вращением вору оси Oy
фиуры, ораниченной линиями y = ln 2, y = ln x, y = 0 и x = 0.
§ 60. Приложения определенного
интеграла к задачам физики
Путь s тела, движущеося со соростью v(t), за время, про-
шедшее от момента t
1
до момента t
2
, вычисляется по формуле
s = v(t)dt.(1)
П р и м е р 1. Тело движется прямолинейно со соростью
v(t) = 2t
2
– t + 1 (м/с). Найти путь, пройденный за первые 5 с.
Р е ш е н и е. Соласно формуле (1), имеем
s(t) = (2t
2
– t + 1) dt = – + t = – + 5 = 75 .
Ответ.75 м.
e
x
e
x–
+
2
---------------------
π
2
---
t
1
t
2
∫
0
5
∫
2t
3
3
-------- -
t
2
2
-----
0
5
250
3
----------
25
2
------
5
6
---
5
6
---

278 Г л а в а 10. Первообразная и интеграл
10. При аих значениях a из промежута [0; 1] площадь
фиуры, ораниченной рафиом фунции f(x) и прямыми x = 0,
x = 1, y = f(a), является наибольшей, а при аих a— наи-
меньшей, если f(x) = ?
11. При аих значениях a площадь фиуры, ораниченной
прямыми x = x
1
, x = x
2
, рафиом фунции y = | sin x + cos x – a |
и осью абсцисс, де x
1
и x
2
— два последовательных эстрему-
ма фунции f(x) = sin x + , является наименьшей?
§ 59. Вычисление объемов тел
Объем V тела, полученноо при вращении вору оси Ox ри-
волинейной трапеции, ораниченной линиями y = f(x) (f(x) l 0),
x = a, x = b (b > a), вычисляется по формуле
V = π f
2
(x)dx.(1)
Объем V тела, образованноо при вращении вору оси Oy
риволинейной трапеции, ораниченной линиями x = ϕ(y)
(ϕ (y) l 0), y = c, y = d (d > c) и осью Oy, вычисляется по фор-
муле
V = πϕ
2
(y)dy.(2)
П р и м е р. Вычислить объем тела, образованноо вращени-
ем одной ари синусоиды (рафиа фунции y = sin x на про-
межуте [0; π]) вору оси Ox.
Р е ш е н и е. По формуле (1) находим
V = π sin
2
x dx = π dx =
= π x + sin 2x = .
Ответ..
1 x
2
–
2
π
4
---
a
b
∫
c
d
∫
0
π
∫
0
π
∫
1cos2x–
2
---------------------------
1
2
---
1
4
---
0
π
π
2
2
----- -
π
2
2
----- -
§ 60. Приложения опред. интеграла к задачам физики 279
1. Вычислите объем тела, образованноо вращением вору
оси абсцисс риволинейной трапеции, ораниченной ипербо-
лой xy = 2, прямыми x = 1, x = 2 и осью абсцисс.
2. Вычислите объем тела, образованноо вращением вору
оси абсцисс фиуры, ораниченной параболами y
2
= x, y = x
2
.
3. Цепная линия y = вращается вору оси абсцисс.
При этом получается поверхность, называемая атеноидом.
Вычислите объем тела, образованноо атеноидом и двумя
плосостями, перпендиулярными оси абсцисс и отстоящими
от начала оординат на расстояния a и b.
4. Вычислите объем тела, полученноо вращением вору
оси ординат фиуры, ораниченной параболой y = 2x – x
2
и
осью абсцисс.
5. Найдите объем тела, полученноо вращением вору
оси Oy риволинейной трапеции, ораниченной линиями
y = arcsin x, y = и x = 0.
6. Найдите объем тела, полученноо вращением вору оси Oy
фиуры, ораниченной линиями y = ln 2, y = ln x, y = 0 и x = 0.
§ 60. Приложения определенного
интеграла к задачам физики
Путь s тела, движущеося со соростью v(t), за время, про-
шедшее от момента t
1
до момента t
2
, вычисляется по формуле
s = v(t)dt.(1)
П р и м е р 1. Тело движется прямолинейно со соростью
v(t) = 2t
2
– t + 1 (м/с). Найти путь, пройденный за первые 5 с.
Р е ш е н и е. Соласно формуле (1), имеем
s(t) = (2t
2
– t + 1) dt = – + t = – + 5 = 75 .
Ответ.75 м.
e
x
e
x–
+
2
---------------------
π
2
---
t
1
t
2
∫
0
5
∫
2t
3
3
-------- -
t
2
2
-----
0
5
250
3
----------
25
2
------
5
6
---
5
6
---
