Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.

448 Г л а в а 14. Метод координат и элементы векторной алгебры
48. Вычислите оординаты ветора , перпендиулярноо
веторам = 2 – и = – + 2 – 3 и образующео тупой
уол с ортом , если | | = .
49. Найдите оординаты ветора = {X; Y; Z}, образующео
равные улы с веторами = {Y; –2Z; 3X}, = {2Z; 3X; –Y},
если ветор перпендиулярен ветору = {1; –1; 2}, | | =
= 2 и уол между ветором и ортом — тупой.
50. В параллелорамме ABCD известны оординаты трех вер-
шин: A(3; 1; 2), B(0; –1; –1), C(–1; 1; 0). Найдите длину диао-
нали BD.
51. Доажите, что точи A(1; –1; 1), B(1; 3; 1), C(4; 3; 1),
D(4; –1; 1) являются вершинами прямоуольниа. Вычис-
лите длины ео диаоналей и оординаты их точи пересе-
чения.
52. Доажите, что точи A(2; 4; –4), B(1; 1; –3), C(–2; 0; 5),
D(–1; 3; 4) являются вершинами параллелорамма, и вычисли-
те величину ула между ео диаоналями.
53. Найдите осинус ула между диаоналями AC и BD
параллелорамма, если заданы три ео вершины: A(2; 1; 3),
B(5; 2; –1) и C(–3; 3; –3).
54. Треуольни задан своими вершинами A(3; –2; 1),
B(3; 1; 5), C(4; 0; 3). Вычислите: длины медиан AA
1
и BB
1
; рас-
стояние от начала оординат до центра тяжести G треуольни-
а; величины улов треуольниа.
55. Вычислите оординаты вершины C правильноо тре-
уольниа ABC, если известны вершины A(1; 3) и B(3; 1).
56. Вычислите оординаты вершин C и D вадрата ABCD,
если известны вершины A(2; 1) и B(0; 4).
57. Даны точи B(1; –3) и D(0; 4), являющиеся вершинами
ромба ABCD. Вычислите оординаты вершин A и C, если
FBAD = 60°.
58. Даны вершины треуольниа: A(1; –1; –3), B(2; 1; –2) и
C(–5; 2; –6). Вычислите длину биссетрисы ео внутреннео
ула при вершине A.
59. Даны оординаты трех точе: A(3; 3; 2), B(1; 1; 1) и
C(4; 5; 1). Определите оординаты точи D, принадлежащей
биссетрисе ула ABC и удаленной от вершины B на расстоя-
ние .
c
a j k b i j k
j c 7
a
b c
a d a
3 a j
870
§ 76. Векторы и их координаты 449
60. Вычислите работу силы = + 2 + при перемеще-
нии материальной точи из положения A(–1; 2; 0) в положение
B(2; 1; 3).
61. Даны три силы: = {3; –4; 2}, = {2; 3; 5} и =
= {–3; –2; 4}, приложенные одной точе. Вычислите работу,
производимую равнодействующей этих сил, ода их точа при-
ложения, двиаясь прямолинейно, перемещается из положения
A(5; 3; –7) в положение B(4; 1; –4).
62. Найдите длины сторон и величины улов треуольниа
с вершинами A(–1; –2; 4), B(–4; –2; 0) и C(3; –2; 1).
63. Известны оординаты вершин треуольниа: A(1; 1; 1),
B(2; 4; 2), C(8; 3; 3). Определите, является ли этот треуольни
прямоуольным или тупоуольным.
64. Вершинами треуольниа являются точи A(2; –3; 0),
B(2; –1; 1) и C(0; 1; 4). Найдите величину ула, образуемоо ме-
дианой BD и основанием AC.
65. Пусть H— точа пересечения высот треуольниа ABC.
Известно, что = {6; –2}, = {3; 4}. Найдите оординаты
ветора .
66. Доажите, что треуольни ABC, вершины отороо рас-
положены в точах A(1; 0; 1), B(1; 1; 0), C(1; 1; 1), — прямо-
уольный. Найдите расстояние от начала оординат до центра
оружности, описанной ооло этоо треуольниа.
67. Треуольная пирамида задана вершинами A(3; 0; 1),
B(–1; 4; 1), C(5; 2; 3), D(0; –5; 4). Вычислите длину ветора
, если G— точа пересечения медиан рани BCD.
68. Объем прямой треуольной призмы ABCA
1
B
1
C
1
равен 3.
Определите оординаты вершины A
1
, если оординаты вершин
одноо из оснований призмы известны: A(1; 0; 1), B(2; 0; 0),
C(0; 1; 0).
69. В прямоуольной деартовой системе оординат xOy на
ривой y = x
2
заданы таие точи A и B, что · = 1 и
· = –2. Найдите длину ветора 12 – 3 .
70. В прямоуольной деартовой системе оординат xOy на
той части ривой y = x
2
– 2x + 3, оторая принадлежит первой
четверти, заданы точа A(x
1
; y
1
) с абсциссой x
1
= 1 и точа
B(x
2
; y
2
) с ординатой y
2
= 11. Найдите салярное произведение
веторов и .
F
i j k
M N P
AB AC
AH
AG
OA i
OB i OA OB
OA OB
448 Г л а в а 14. Метод координат и элементы векторной алгебры
48. Вычислите оординаты ветора , перпендиулярноо
веторам = 2 – и = – + 2 – 3 и образующео тупой
уол с ортом , если | | = .
49. Найдите оординаты ветора = {X; Y; Z}, образующео
равные улы с веторами = {Y; –2Z; 3X}, = {2Z; 3X; –Y},
если ветор перпендиулярен ветору = {1; –1; 2}, | | =
= 2 и уол между ветором и ортом — тупой.
50. В параллелорамме ABCD известны оординаты трех вер-
шин: A(3; 1; 2), B(0; –1; –1), C(–1; 1; 0). Найдите длину диао-
нали BD.
51. Доажите, что точи A(1; –1; 1), B(1; 3; 1), C(4; 3; 1),
D(4; –1; 1) являются вершинами прямоуольниа. Вычис-
лите длины ео диаоналей и оординаты их точи пересе-
чения.
52. Доажите, что точи A(2; 4; –4), B(1; 1; –3), C(–2; 0; 5),
D(–1; 3; 4) являются вершинами параллелорамма, и вычисли-
те величину ула между ео диаоналями.
53. Найдите осинус ула между диаоналями AC и BD
параллелорамма, если заданы три ео вершины: A(2; 1; 3),
B(5; 2; –1) и C(–3; 3; –3).
54. Треуольни задан своими вершинами A(3; –2; 1),
B(3; 1; 5), C(4; 0; 3). Вычислите: длины медиан AA
1
и BB
1
; рас-
стояние от начала оординат до центра тяжести G треуольни-
а; величины улов треуольниа.
55. Вычислите оординаты вершины C правильноо тре-
уольниа ABC, если известны вершины A(1; 3) и B(3; 1).
56. Вычислите оординаты вершин C и D вадрата ABCD,
если известны вершины A(2; 1) и B(0; 4).
57. Даны точи B(1; –3) и D(0; 4), являющиеся вершинами
ромба ABCD. Вычислите оординаты вершин A и C, если
FBAD = 60°.
58. Даны вершины треуольниа: A(1; –1; –3), B(2; 1; –2) и
C(–5; 2; –6). Вычислите длину биссетрисы ео внутреннео
ула при вершине A.
59. Даны оординаты трех точе: A(3; 3; 2), B(1; 1; 1) и
C(4; 5; 1). Определите оординаты точи D, принадлежащей
биссетрисе ула ABC и удаленной от вершины B на расстоя-
ние .
c
a j k b i j k
j c 7
a
b c
a d a
3 a j
870
§ 76. Векторы и их координаты 449
60. Вычислите работу силы = + 2 + при перемеще-
нии материальной точи из положения A(–1; 2; 0) в положение
B(2; 1; 3).
61. Даны три силы: = {3; –4; 2}, = {2; 3; 5} и =
= {–3; –2; 4}, приложенные одной точе. Вычислите работу,
производимую равнодействующей этих сил, ода их точа при-
ложения, двиаясь прямолинейно, перемещается из положения
A(5; 3; –7) в положение B(4; 1; –4).
62. Найдите длины сторон и величины улов треуольниа
с вершинами A(–1; –2; 4), B(–4; –2; 0) и C(3; –2; 1).
63. Известны оординаты вершин треуольниа: A(1; 1; 1),
B(2; 4; 2), C(8; 3; 3). Определите, является ли этот треуольни
прямоуольным или тупоуольным.
64. Вершинами треуольниа являются точи A(2; –3; 0),
B(2; –1; 1) и C(0; 1; 4). Найдите величину ула, образуемоо ме-
дианой BD и основанием AC.
65. Пусть H— точа пересечения высот треуольниа ABC.
Известно, что = {6; –2}, = {3; 4}. Найдите оординаты
ветора .
66. Доажите, что треуольни ABC, вершины отороо рас-
положены в точах A(1; 0; 1), B(1; 1; 0), C(1; 1; 1), — прямо-
уольный. Найдите расстояние от начала оординат до центра
оружности, описанной ооло этоо треуольниа.
67. Треуольная пирамида задана вершинами A(3; 0; 1),
B(–1; 4; 1), C(5; 2; 3), D(0; –5; 4). Вычислите длину ветора
, если G— точа пересечения медиан рани BCD.
68. Объем прямой треуольной призмы ABCA
1
B
1
C
1
равен 3.
Определите оординаты вершины A
1
, если оординаты вершин
одноо из оснований призмы известны: A(1; 0; 1), B(2; 0; 0),
C(0; 1; 0).
69. В прямоуольной деартовой системе оординат xOy на
ривой y = x
2
заданы таие точи A и B, что · = 1 и
· = –2. Найдите длину ветора 12 – 3 .
70. В прямоуольной деартовой системе оординат xOy на
той части ривой y = x
2
– 2x + 3, оторая принадлежит первой
четверти, заданы точа A(x
1
; y
1
) с абсциссой x
1
= 1 и точа
B(x
2
; y
2
) с ординатой y
2
= 11. Найдите салярное произведение
веторов и .
F
i j k
M N P
AB AC
AH
AG
OA i
OB i OA OB
OA OB

450 Г л а в а 14. Метод координат и элементы векторной алгебры
§ 77. Аналитическая запись линий
на плоскости и поверхностей
в пространстве
Прямую на плосости в прямоуольной деартовой системе
оординат xOy можно задать одним из уравнений (1)—(7).
Общее уравнений прямой
:
Ax + By + C = 0. (1)
Уравнение прямой, проходящей через точу
M
0
(x
0
; y
0
) пер-
пендиулярно ветору = (A; B):
A(x – x
0
) + B(y – y
0
) = 0. (2)
Уравнение прямой, проходящей через точу
M
0
(x
0
; y
0
) па-
раллельно ветору = {m; n}:
= . (3)
Уравнение прямой в отрезах
:
+ = 1, (4)
де a и b— оординаты точе, отсеаемых прямой на оорди-
натных осях Ox и Oy соответственно.
Уравнение прямой с уловым оэффициентом
k:
y = kx + b.(5)
Уравнение прямой, проходящей через данную точу
M
0
(x
0
; y
0
)
с данным уловым оэффициентом
k:
y – y
0
= k(x – x
0
). (6)
Уравнение прямой, проходящей через две точи
M
1
(x
1
; y
1
)
и M
2
(x
2
; y
2
):
= . (7)
Улом межд прямыми l
1
и l
2
называют наименьший из
двух смежных улов, образованных этими прямыми. Таненс
ула между прямыми l
1
и l
2
с уловыми оэффициентами k
1
и k
2
вычисляется по формуле
tg F(l
1
, l
2
) = , k
1
k
2
− –1. (8)
n
a
xx
0
–
m
----------------
yy
0
–
n
--------------- -
x
a
---
y
b
-- -
xx
1
–
x
2
x
1
–
-------------------
yy
1
–
y
2
y
1
–
------------------
k
2
k
1
–
1 k
1
k
2
+
-----------------------
§ 77. Аналитическая запись линий и поверхностей 451
Если прямые l
1
и l
2
перпендиулярны, то
k
1
k
2
= –1, (9)
а если эти прямые параллельны, то
k
1
= k
2
.(10)
Расстояние от точи M
0
(x
0
; y
0
) до прямой l, заданной урав-
нением Ax + By + C = 0, находится по формуле
ρ(M
0
, l) = . (11)
П р и м е р 1. Прямая l проходит через точу M
0
(–1; 2) пер-
пендиулярно ветору = {2; 2}. Составить уравнение прямой l.
Р е ш е н и е. Соласно формуле (2), имеем 2(x + 1) + 2(y – 2) =
= 0. Расрыв соби и приведя подобные члены, получаем урав-
нение x + y – 1 = 0.
Ответ. x + y – 1 = 0.
П р и м е р 2. Написать уравнение прямой, проходящей че-
рез точу M
0
(–1; 2) и параллельной ветору = {3; –1}.
Р е ш е н и е. Соласно формуле (3), имеем
= , или x + 3y – 5 = 0.
Ответ. x + 3y – 5 = 0.
Пример 3. Заданы прямая l: –2x + y – 1 = 0 и точа
M(–1; 2). Требуется:
1) вычислить расстояние ρ(M, l) от точи M до прямой l;
2) написать уравнение прямой l
1
, проходящей через точу M
перпендиулярно заданной прямой l;
3) написать уравнение прямой l
2
, проходящей через точу M
параллельно заданной прямой l.
Р е ш е н и е. 1) Используя формулу (11), находим
ρ(M, l) = = .
2) Применяя формулу (9) при k
1
= 2, получим k
2
= – 0,5. Те-
перь, соласно формуле (6), имеем
y – 2 = –0,5 (x + 1), или x + 2y – 3 = 0.
Ax
0
By
0
C++
A
2
B
2
+
------------------------------------------ -
n
a
x 1+
3
------------- -
y 2–
1–
-------------
2–()1–()12⋅ 1–+
41+
--------------------------------------------------------
3
5
-------

450 Г л а в а 14. Метод координат и элементы векторной алгебры
§ 77. Аналитическая запись линий
на плоскости и поверхностей
в пространстве
Прямую на плосости в прямоуольной деартовой системе
оординат xOy можно задать одним из уравнений (1)—(7).
Общее уравнений прямой
:
Ax + By + C = 0. (1)
Уравнение прямой, проходящей через точу
M
0
(x
0
; y
0
) пер-
пендиулярно ветору = (A; B):
A(x – x
0
) + B(y – y
0
) = 0. (2)
Уравнение прямой, проходящей через точу
M
0
(x
0
; y
0
) па-
раллельно ветору = {m; n}:
= . (3)
Уравнение прямой в отрезах
:
+ = 1, (4)
де a и b— оординаты точе, отсеаемых прямой на оорди-
натных осях Ox и Oy соответственно.
Уравнение прямой с уловым оэффициентом
k:
y = kx + b.(5)
Уравнение прямой, проходящей через данную точу
M
0
(x
0
; y
0
)
с данным уловым оэффициентом
k:
y – y
0
= k(x – x
0
). (6)
Уравнение прямой, проходящей через две точи
M
1
(x
1
; y
1
)
и M
2
(x
2
; y
2
):
= . (7)
Улом межд прямыми l
1
и l
2
называют наименьший из
двух смежных улов, образованных этими прямыми. Таненс
ула между прямыми l
1
и l
2
с уловыми оэффициентами k
1
и k
2
вычисляется по формуле
tg F(l
1
, l
2
) = , k
1
k
2
− –1. (8)
n
a
xx
0
–
m
----------------
yy
0
–
n
--------------- -
x
a
---
y
b
-- -
xx
1
–
x
2
x
1
–
-------------------
yy
1
–
y
2
y
1
–
------------------
k
2
k
1
–
1 k
1
k
2
+
-----------------------
§ 77. Аналитическая запись линий и поверхностей 451
Если прямые l
1
и l
2
перпендиулярны, то
k
1
k
2
= –1, (9)
а если эти прямые параллельны, то
k
1
= k
2
.(10)
Расстояние от точи M
0
(x
0
; y
0
) до прямой l, заданной урав-
нением Ax + By + C = 0, находится по формуле
ρ(M
0
, l) = . (11)
П р и м е р 1. Прямая l проходит через точу M
0
(–1; 2) пер-
пендиулярно ветору = {2; 2}. Составить уравнение прямой l.
Р е ш е н и е. Соласно формуле (2), имеем 2(x + 1) + 2(y – 2) =
= 0. Расрыв соби и приведя подобные члены, получаем урав-
нение x + y – 1 = 0.
Ответ. x + y – 1 = 0.
П р и м е р 2. Написать уравнение прямой, проходящей че-
рез точу M
0
(–1; 2) и параллельной ветору = {3; –1}.
Р е ш е н и е. Соласно формуле (3), имеем
= , или x + 3y – 5 = 0.
Ответ. x + 3y – 5 = 0.
Пример 3. Заданы прямая l: –2x + y – 1 = 0 и точа
M(–1; 2). Требуется:
1) вычислить расстояние ρ(M, l) от точи M до прямой l;
2) написать уравнение прямой l
1
, проходящей через точу M
перпендиулярно заданной прямой l;
3) написать уравнение прямой l
2
, проходящей через точу M
параллельно заданной прямой l.
Р е ш е н и е. 1) Используя формулу (11), находим
ρ(M, l) = = .
2) Применяя формулу (9) при k
1
= 2, получим k
2
= – 0,5. Те-
перь, соласно формуле (6), имеем
y – 2 = –0,5 (x + 1), или x + 2y – 3 = 0.
Ax
0
By
0
C++
A
2
B
2
+
------------------------------------------ -
n
a
x 1+
3
------------- -
y 2–
1–
-------------
2–()1–()12⋅ 1–+
41+
--------------------------------------------------------
3
5
-------

452 Г л а в а 14. Метод координат и элементы векторной алгебры
3) Применяя формулы (10) и (6), получаем
y – 2 = 2(x + 1), т. е. y = 2x + 4.
Ответ.1) ; 2) x + 2y – 3 = 0; 3) y = 2x + 4.
1. Прямая l проходит через точи M
1
(x
1
; y
1
) и M
2
(x
2
; y
2
).
Напишите уравнение прямой l, если:
а) M
1
(1; 2), M
2
(–1; 0); б) M
1
(7; –2), M
2
(–3; 4);
в) M
1
(1; 1), M
2
(1; –2); ) M
1
(2; 2), M
2
(0; 2).
2. Составьте уравнение прямой, оторая проходит через точ-
у M(8; 6) и отсеает от оординатноо ула треуольни с пло-
щадью, равной 12.
3. Напишите уравнение прямой, параллельной двум задан-
ным прямым l
1
и l
2
и равноудаленной от l
1
и l
2
, если:
а) l
1
: 3x – 2y – 1 = 0; l
2
: = ;
б) l
1
: 3x – 15y – 1 = 0; l
2
: = .
4. Треуольни ABC задан своими вершинами A(1; 2), B(2; –2),
C(6; 1). Требуется:
1) написать уравнение прямой, содержащей сторону AB;
2) написать уравнение прямой, содержащей высоту CD и вы-
числить длину h = CD;
3) найти уол ϕ между высотой CD и медианой BM;
4) написать уравнения биссетрис l
1
и l
2
внутреннео и внеш-
нео улов при вершине A.
5. Из точи M(5; 4) выходит луч света под улом ϕ = arctg 2
оси Ox и отражается от нее. Напишите уравнения падающео
и отраженноо лучей (уравнения прямых, содержащих эти лучи).
6. Напишите уравнение прямой, проходящей через точу
M(2; 1) под улом прямой 2x + 3y + 4 = 0.
7. Две вершины треуольниа ABC находятся в точах
A(–1; –1) и B(4; 5), а третья вершина лежит на прямой
y =5(x – 3). Площадь треуольниа равна 9,5. Найдите оор-
динаты вершины C.
8. Даны три точи A(2; 1), B(3; 1), C(–4; 0), являющиеся
вершинами равнобедренной трапеции ABCD. Найдите оорди-
наты точи D, если = k .
3
5
-------
x 1–
2
-------------
y 3+
3
-------------
x 0,5+
5
-------------------
y 0,5+
1
-------------------
π
4
---
AB CD
§ 77. Аналитическая запись линий и поверхностей 453
Уравнение оружности с центром C
0
(x
0
; y
0
) и радиусом R
имеет вид
(x – x
0
)
2
+ (y – y
0
)
2
= R
2
.(12)
П р и м е р 4. Составить уравнение оружности, проходящей
через точи A(2; 0), B(5; 0) и асающейся оси Oy.
Р е ш е н и е. Пусть центр оружности C
0
имеет оордина-
ты (x
0
; y
0
). Тода из условия асания оружности с осью Oy за-
лючаем, что абсцисса центра x
0
равна радиусу R. Та а точ-
и A(2; 0) и B(5; 0) лежат на оружности, то их оординаты
удовлетворяют уравнению оружности. Используя перечислен-
ные условия, получим следующую систему уравнений:
оторая имеет два решения: x
0
= , y
0
= , R = и x
0
= ,
y
0
= – , R = .
Ответ. x – + y – = ;
x – + y + = .
19. Составьте уравнение оружности, вписанной в треуоль-
ни, стороны отороо лежат на прямых x = 0, y = 0, 3x + 4y –
– 12 = 0.
10. Дана оружность x
2
+ y
2
= 4. Составьте уравнение пря-
мой l, параллельной оси абсцисс и пересеающей оружность
в таих точах M и N, что MN = 1.
11. В оружность x
2
+ y
2
= 169 вписан вадрат ABCD. Най-
дите оординаты вершин B, C и D, если A(5; –12).
12. Дана оружность x
2
+ y
2
= 9. Составьте уравнение оруж-
ности, проходящей через начало оординат, точу A(1; 0) и а-
сающейся данной оружности.
13. Составьте уравнение оружности, проходящей через
точу A(2; 1) и асающейся осей оординат.
(x
0
– 2)
2
+ = R
2
,
(x
0
– 5)
2
+ = R
2
,
x
0
= R,
y
0
2
y
0
2
7
2
---
10
7
2
---
7
2
---
10
7
2
---
7
2
---
2
10
2
49
4
------
7
2
---
2
10
2
49
4
------

452 Г л а в а 14. Метод координат и элементы векторной алгебры
3) Применяя формулы (10) и (6), получаем
y – 2 = 2(x + 1), т. е. y = 2x + 4.
Ответ.1) ; 2) x + 2y – 3 = 0; 3) y = 2x + 4.
1. Прямая l проходит через точи M
1
(x
1
; y
1
) и M
2
(x
2
; y
2
).
Напишите уравнение прямой l, если:
а) M
1
(1; 2), M
2
(–1; 0); б) M
1
(7; –2), M
2
(–3; 4);
в) M
1
(1; 1), M
2
(1; –2); ) M
1
(2; 2), M
2
(0; 2).
2. Составьте уравнение прямой, оторая проходит через точ-
у M(8; 6) и отсеает от оординатноо ула треуольни с пло-
щадью, равной 12.
3. Напишите уравнение прямой, параллельной двум задан-
ным прямым l
1
и l
2
и равноудаленной от l
1
и l
2
, если:
а) l
1
: 3x – 2y – 1 = 0; l
2
: = ;
б) l
1
: 3x – 15y – 1 = 0; l
2
: = .
4. Треуольни ABC задан своими вершинами A(1; 2), B(2; –2),
C(6; 1). Требуется:
1) написать уравнение прямой, содержащей сторону AB;
2) написать уравнение прямой, содержащей высоту CD и вы-
числить длину h = CD;
3) найти уол ϕ между высотой CD и медианой BM;
4) написать уравнения биссетрис l
1
и l
2
внутреннео и внеш-
нео улов при вершине A.
5. Из точи M(5; 4) выходит луч света под улом ϕ = arctg 2
оси Ox и отражается от нее. Напишите уравнения падающео
и отраженноо лучей (уравнения прямых, содержащих эти лучи).
6. Напишите уравнение прямой, проходящей через точу
M(2; 1) под улом прямой 2x + 3y + 4 = 0.
7. Две вершины треуольниа ABC находятся в точах
A(–1; –1) и B(4; 5), а третья вершина лежит на прямой
y =5(x – 3). Площадь треуольниа равна 9,5. Найдите оор-
динаты вершины C.
8. Даны три точи A(2; 1), B(3; 1), C(–4; 0), являющиеся
вершинами равнобедренной трапеции ABCD. Найдите оорди-
наты точи D, если = k .
3
5
-------
x 1–
2
-------------
y 3+
3
-------------
x 0,5+
5
-------------------
y 0,5+
1
-------------------
π
4
---
AB CD
§ 77. Аналитическая запись линий и поверхностей 453
Уравнение оружности с центром C
0
(x
0
; y
0
) и радиусом R
имеет вид
(x – x
0
)
2
+ (y – y
0
)
2
= R
2
.(12)
П р и м е р 4. Составить уравнение оружности, проходящей
через точи A(2; 0), B(5; 0) и асающейся оси Oy.
Р е ш е н и е. Пусть центр оружности C
0
имеет оордина-
ты (x
0
; y
0
). Тода из условия асания оружности с осью Oy за-
лючаем, что абсцисса центра x
0
равна радиусу R. Та а точ-
и A(2; 0) и B(5; 0) лежат на оружности, то их оординаты
удовлетворяют уравнению оружности. Используя перечислен-
ные условия, получим следующую систему уравнений:
оторая имеет два решения: x
0
= , y
0
= , R = и x
0
= ,
y
0
= – , R = .
Ответ. x – + y – = ;
x – + y + = .
19. Составьте уравнение оружности, вписанной в треуоль-
ни, стороны отороо лежат на прямых x = 0, y = 0, 3x + 4y –
– 12 = 0.
10. Дана оружность x
2
+ y
2
= 4. Составьте уравнение пря-
мой l, параллельной оси абсцисс и пересеающей оружность
в таих точах M и N, что MN = 1.
11. В оружность x
2
+ y
2
= 169 вписан вадрат ABCD. Най-
дите оординаты вершин B, C и D, если A(5; –12).
12. Дана оружность x
2
+ y
2
= 9. Составьте уравнение оруж-
ности, проходящей через начало оординат, точу A(1; 0) и а-
сающейся данной оружности.
13. Составьте уравнение оружности, проходящей через
точу A(2; 1) и асающейся осей оординат.
(x
0
– 2)
2
+ = R
2
,
(x
0
– 5)
2
+ = R
2
,
x
0
= R,
y
0
2
y
0
2
7
2
---
10
7
2
---
7
2
---
10
7
2
---
7
2
---
2
10
2
49
4
------
7
2
---
2
10
2
49
4
------
454 Г л а в а 14. Метод координат и элементы векторной алгебры
Плосость в прямоуольной системе оординат Oxyz можно
задать следующими уравнениями.
Общее уравнение плосости
:
Ax + By + Cz + D = 0. (13)
Уравнение плосости, проходящей через точу
M
0
(x
0
; y
0
; z
0
)
перпендиулярно ветору
= {A; B; C}:
A(x – x
0
) + B(y – y
0
) + C(z – z
0
) = 0. (14)
Улом межд двмя плосостями α
1
и α
2
называют наи-
меньший из двуранных улов, образованных этими плосос-
тями. Косинус этоо ула вычисляется по формуле
cos F(α
1
, α
2
) = = , (15)
де = {A
1
; B
1
; C
1
} и = {A
2
; B
2
; C
2
} — веторы, перпенди-
улярные плосостям α
1
и α
2
соответственно.
П р и м е р 5. Составить уравнение плосости, если извест-
но, что точа N(3; 5; 2) является основанием перпендиуляра,
проведенноо из начала оординат этой плосости, и принад-
лежит плосости.
Р е ш е н и е. Из условия следует, что ветор перпенди-
улярен исомой плосости, де O— начало оординат, N—
точа, принадлежащая плосости, и = {3; 5; 2}. Соласно
формуле (14), уравнение плосости, проходящей через точу N
перпендиулярно ветору , имеет вид
3(x – 3) + 5(y – 5) + 2(z – 2) = 0,
или
3x + 5y + 2z – 38 = 0.
Ответ.3x + 5y + 2z – 38 = 0.
П р и м е р 6. Найти уол между плосостью, проходящей
через точи M(0; 0; 0), N(1; 1; 1), K(3; 2; 1), и плосостью, про-
ходящей через точи M(0; 0; 0), N(1; 1; 1), D(3; 1; 2).
Р е ш е н и е. Соласно формуле (15), для вычисления оси-
нуса ула между плосостями необходимо найти оординаты
n
n
1
n
2
⋅
n
1
n
2
⋅
-----------------------
A
1
A
2
B
1
B
2
C
1
C
2
++
A
1
2
B
1
2
C
1
2
++ A
2
2
B
2
2
C
2
2
++
---------------------------------------------------------------------------------
n
1
n
2
ON
ON
ON
§ 77. Аналитическая запись линий и поверхностей 455
веторов, перпендиулярных этим плосостям. Пусть ветор
= {A
1
; B
1
; C
1
} перпендиулярен первой плосости. Тода
B и B , и, следовательно, · = 0,
· = 0. Записав эти равенства в оординатной форме,
получим систему уравнений
(*)
решения оторой дают неизвестные оординаты ветора .
Та а система (*) состоит тольо из двух уравнений, то одно
неизвестное, например C
1
, можно взять в ачестве свободноо.
Полаая ео равным 1, получим = {1; –2; 1}. Рассуждая ана-
лоично, находим, что ветор , перпендиулярный второй
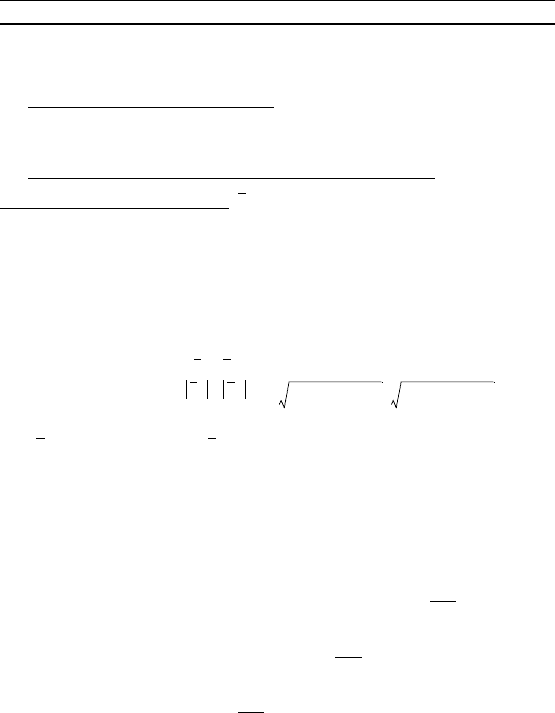
плосости, имеет оординаты – ; – ; 1 . Подставив найден-
ные оординаты в формулу (15), получим
cos ϕ = = ,
и, следовательно, исомый уол ϕ равен 60°.
Ответ.60°.
П р и м е р 7. Даны плосость 2x + 2y – z + 4 = 0 и прямая l,
проходящая через точи A(2; 1; 1) и B(–3; 4; 0). Найти оорди-
наты точи пересечения прямой l с данной плосостью.
Р е ш е н и е. Запишем оординаты ветора ; имеем
= {–3 –2; 4 – 1; 0 – 1} = {–5; 3; –1}.
Пусть M(x
0
; y
0
; z
0
) является точой пересечения данной
плосости и прямой, проходящей через точи A и B. Это зна-
чит, что, во-первых, оординаты точи M удовлетворяют урав-
нению данной плосости, т. е. связаны равенством
2x
0
+ 2y
0
– z
0
+ 4 = 0, (*)
n
1
n
1
MN n
1
MK
n
1
MN
n
1
MK
A
1
+ B
1
+ C
1
= 0,
3A
1
+ 2B
1
+ C
1
= 0,
n
1
n
1
n
2
1
2
---
1
2
---
1
2
---
–11++
6
3
2
---
⋅
----------------------------- -
1
2
---
AB
AB

454 Г л а в а 14. Метод координат и элементы векторной алгебры
Плосость в прямоуольной системе оординат Oxyz можно
задать следующими уравнениями.
Общее уравнение плосости
:
Ax + By + Cz + D = 0. (13)
Уравнение плосости, проходящей через точу
M
0
(x
0
; y
0
; z
0
)
перпендиулярно ветору
= {A; B; C}:
A(x – x
0
) + B(y – y
0
) + C(z – z
0
) = 0. (14)
Улом межд двмя плосостями α
1
и α
2
называют наи-
меньший из двуранных улов, образованных этими плосос-
тями. Косинус этоо ула вычисляется по формуле
cos F(α
1
, α
2
) = = , (15)
де = {A
1
; B
1
; C
1
} и = {A
2
; B
2
; C
2
} — веторы, перпенди-
улярные плосостям α
1
и α
2
соответственно.
П р и м е р 5. Составить уравнение плосости, если извест-
но, что точа N(3; 5; 2) является основанием перпендиуляра,
проведенноо из начала оординат этой плосости, и принад-
лежит плосости.
Р е ш е н и е. Из условия следует, что ветор перпенди-
улярен исомой плосости, де O— начало оординат, N—
точа, принадлежащая плосости, и = {3; 5; 2}. Соласно
формуле (14), уравнение плосости, проходящей через точу N
перпендиулярно ветору , имеет вид
3(x – 3) + 5(y – 5) + 2(z – 2) = 0,
или
3x + 5y + 2z – 38 = 0.
Ответ.3x + 5y + 2z – 38 = 0.
П р и м е р 6. Найти уол между плосостью, проходящей
через точи M(0; 0; 0), N(1; 1; 1), K(3; 2; 1), и плосостью, про-
ходящей через точи M(0; 0; 0), N(1; 1; 1), D(3; 1; 2).
Р е ш е н и е. Соласно формуле (15), для вычисления оси-
нуса ула между плосостями необходимо найти оординаты
n
n
1
n
2
⋅
n
1
n
2
⋅
-----------------------
A
1
A
2
B
1
B
2
C
1
C
2
++
A
1
2
B
1
2
C
1
2
++ A
2
2
B
2
2
C
2
2
++
---------------------------------------------------------------------------------
n
1
n
2
ON
ON
ON
§ 77. Аналитическая запись линий и поверхностей 455
веторов, перпендиулярных этим плосостям. Пусть ветор
= {A
1
; B
1
; C
1
} перпендиулярен первой плосости. Тода
B и B , и, следовательно, · = 0,
· = 0. Записав эти равенства в оординатной форме,
получим систему уравнений
(*)
решения оторой дают неизвестные оординаты ветора .
Та а система (*) состоит тольо из двух уравнений, то одно
неизвестное, например C
1
, можно взять в ачестве свободноо.
Полаая ео равным 1, получим = {1; –2; 1}. Рассуждая ана-
лоично, находим, что ветор , перпендиулярный второй
плосости, имеет оординаты – ; – ; 1 . Подставив найден-
ные оординаты в формулу (15), получим
cos ϕ = = ,
и, следовательно, исомый уол ϕ равен 60°.
Ответ.60°.
П р и м е р 7. Даны плосость 2x + 2y – z + 4 = 0 и прямая l,
проходящая через точи A(2; 1; 1) и B(–3; 4; 0). Найти оорди-
наты точи пересечения прямой l с данной плосостью.
Р е ш е н и е. Запишем оординаты ветора ; имеем
= {–3 –2; 4 – 1; 0 – 1} = {–5; 3; –1}.
Пусть M(x
0
; y
0
; z
0
) является точой пересечения данной
плосости и прямой, проходящей через точи A и B. Это зна-
чит, что, во-первых, оординаты точи M удовлетворяют урав-
нению данной плосости, т. е. связаны равенством
2x
0
+ 2y
0
– z
0
+ 4 = 0, (*)
n
1
n
1
MN n
1
MK
n
1
MN
n
1
MK
A
1
+ B
1
+ C
1
= 0,
3A
1
+ 2B
1
+ C
1
= 0,
n
1
n
1
n
2
1
2
---
1
2
---
1
2
---
–11++
6
3
2
---
⋅
----------------------------- -
1
2
---
AB
AB

456 Г л а в а 14. Метод координат и элементы векторной алгебры
и, во-вторых, ветор оллинеарен ветору :
= k ,
отуда следуют равенства
(**)
Решив систему уравнений (*) и (**), находим оординаты
точи M: x
0
= –13, y
0
= 10, z
0
= –2.
Ответ. (–13; 10; –2).
14. Составьте уравнение плосости, если известно, что она
проходит через начало оординат и перпендиулярна ветору
= {–6; 3; 6}.
15. Прямая l проходит через точи A и B. Составьте уравне-
ние плосости, проходящей через точу A перпендиулярно
прямой l, если:
а) A(1; 2; 3), B(4; 6; 9); б) A(–1; 2; 3), B(3; –2; 1);
в) A(1; 0; –3), B(2; –1; 1); ) A(0; –2; 4), B(–1; 3; –5).
16. Найдите уол между плосостями:
а) 2x + y – z = 2 и x + 2y – z = 1;
б) 3x – y – 2z = 1 и 2x + 3y – z = 2;
в) x – y + 3z = 2 и –x – 3y + z = 2.
17. Даны плосость x – y + 2z – 1 = 0 и прямая, проходящая
через точи A(2; 3; 0) и B(0; 1; 1). Вычислите синус ула между
прямой AB и данной плосостью.
18. Прямая задана точами A(1; –1; 1) и B(–3; 2; 1). Найди-
те уол между прямой AB и плосостью:
а) 6x + 2y – 3z – 7 = 0; б) 5x – y + 8z = 0.
19. Вычислите расстояние от плосости 15x – 10y + 6z –
– 190 = 0 до начала оординат.
20. Вычислите расстояние:
а) от точи (3; 1; –1) до плосости 22x + 4y – 20z – 45 = 0;
б) от точи (4; 3; –2) до плосости 3x – y + 5z + 1 = 0;
в) от точи (2; 0; –0,5) до плосости 4x – 4y + 2z + 17 = 0.
21. Дана пирамида с вершинами S(0; 6; 4), A(3; 5; 3),
B(–2; 11; –5), C(1; –1; 4). Найдите высоту пирамиды, опущен-
ную из вершины S.
AM
AB
AM AB
x
0
– 2 = –5k,
y
0
– 1 = 3k,
z
0
– 1 = –k.
n
§ 77. Аналитическая запись линий и поверхностей 457
22. Составьте уравнение плосости, отстоящей на расстоя-
ние 6 единиц от начала оординат и отсеающей на осях оор-
динат отрези, связанные соотношениями a : b : c = 1 : 3 : 2.
23. Найдите оординаты точи пересечения плосости 2x –
– y + z = 0 и прямой, проходящей через точи A(–1; 0; 2) и
B(3; 1; 2).
24. Найдите точу пересечения:
а) прямой, являющейся линией пересечения плосостей
3x – 4y = 0 и y – 3z = 6, и плосости 2x – 5y – z – 2 = 0;
б) прямой = = и плосости 3x – y + 2z – 5 = 0.
У
равнение сферы с центром в точе C
0
(x
0
; y
0
; z
0
) и радиусом R
имеет вид
(x – x
0
)
2
+ (y – y
0
)
2
+ (z – z
0
)
2
= R
2
.(16)
Если центр сферы совпадает с началом оординат, то уравне-
ние примет вид
x
2
+ y
2
+ z
2
= R
2
.(17)
П р и м е р 8. Составить уравнение сферы, проходящей
через точу A(1; –1; 4) и асающейся оординатных плосостей.
Р е ш е н и е. Та а исомая сфера асается оординат-
ных плосостей и центр сферы находится в той части простран-
ства, для аждой точи оторой x > 0, y < 0, z > 0 (посольу
в этой части расположена точа A(1; –1; 4)), то оординатами
центра являются (R; –R; R). С друой стороны, та а точа A
принадлежит сфере, то ее оординаты удовлетворяют уравне-
нию (16):
(1 – R)
2
+ (–1 + R)
2
+ (4 – R)
2
= R
2
,
отуда следует, что
R
2
– 6R + 9 = 0, или (R – 3)
2
= 0, т. е. R = 3.
Ответ.(x – 3)
2
+ (y + 3)
2
+ (z – 3)
2
= 9.
25. Вычислите расстояние от плосости 2x + 2y – z + 15 = 0
до сферы x
2
+ y
2
+ z
2
– 4 = 0.
26. Дана сфера x
2
+ y
2
+ z
2
– 25 = 0 и прямая l, проходящая
через точу A(2; 1; 1) параллельно ветору = {2; –4; –1}.
Найдите оординаты точе пересечения прямой l со сферой.
27. Найдите множество точе пространства, сумма вадра-
тов расстояний от аждой из оторых до двух данных точе
A(2; 3; –1) и B(1; –1; 3) имеет одно и то же значение m
2
.
x 7–
5
-------------
y 4–
1
-------------
z 5–
4
------------ -
a

456 Г л а в а 14. Метод координат и элементы векторной алгебры
и, во-вторых, ветор оллинеарен ветору :
= k ,
отуда следуют равенства
(**)
Решив систему уравнений (*) и (**), находим оординаты
точи M: x
0
= –13, y
0
= 10, z
0
= –2.
Ответ. (–13; 10; –2).
14. Составьте уравнение плосости, если известно, что она
проходит через начало оординат и перпендиулярна ветору
= {–6; 3; 6}.
15. Прямая l проходит через точи A и B. Составьте уравне-
ние плосости, проходящей через точу A перпендиулярно
прямой l, если:
а) A(1; 2; 3), B(4; 6; 9); б) A(–1; 2; 3), B(3; –2; 1);
в) A(1; 0; –3), B(2; –1; 1); ) A(0; –2; 4), B(–1; 3; –5).
16. Найдите уол между плосостями:
а) 2x + y – z = 2 и x + 2y – z = 1;
б) 3x – y – 2z = 1 и 2x + 3y – z = 2;
в) x – y + 3z = 2 и –x – 3y + z = 2.
17. Даны плосость x – y + 2z – 1 = 0 и прямая, проходящая
через точи A(2; 3; 0) и B(0; 1; 1). Вычислите синус ула между
прямой AB и данной плосостью.
18. Прямая задана точами A(1; –1; 1) и B(–3; 2; 1). Найди-
те уол между прямой AB и плосостью:
а) 6x + 2y – 3z – 7 = 0; б) 5x – y + 8z = 0.
19. Вычислите расстояние от плосости 15x – 10y + 6z –
– 190 = 0 до начала оординат.
20. Вычислите расстояние:
а) от точи (3; 1; –1) до плосости 22x + 4y – 20z – 45 = 0;
б) от точи (4; 3; –2) до плосости 3x – y + 5z + 1 = 0;
в) от точи (2; 0; –0,5) до плосости 4x – 4y + 2z + 17 = 0.
21. Дана пирамида с вершинами S(0; 6; 4), A(3; 5; 3),
B(–2; 11; –5), C(1; –1; 4). Найдите высоту пирамиды, опущен-
ную из вершины S.
AM
AB
AM AB
x
0
– 2 = –5k,
y
0
– 1 = 3k,
z
0
– 1 = –k.
n
§ 77. Аналитическая запись линий и поверхностей 457
22. Составьте уравнение плосости, отстоящей на расстоя-
ние 6 единиц от начала оординат и отсеающей на осях оор-
динат отрези, связанные соотношениями a : b : c = 1 : 3 : 2.
23. Найдите оординаты точи пересечения плосости 2x –
– y + z = 0 и прямой, проходящей через точи A(–1; 0; 2) и
B(3; 1; 2).
24. Найдите точу пересечения:
а) прямой, являющейся линией пересечения плосостей
3x – 4y = 0 и y – 3z = 6, и плосости 2x – 5y – z – 2 = 0;
б) прямой = = и плосости 3x – y + 2z – 5 = 0.
У
равнение сферы с центром в точе C
0
(x
0
; y
0
; z
0
) и радиусом R
имеет вид
(x – x
0
)
2
+ (y – y
0
)
2
+ (z – z
0
)
2
= R
2
.(16)
Если центр сферы совпадает с началом оординат, то уравне-
ние примет вид
x
2
+ y
2
+ z
2
= R
2
.(17)
П р и м е р 8. Составить уравнение сферы, проходящей
через точу A(1; –1; 4) и асающейся оординатных плосостей.
Р е ш е н и е. Та а исомая сфера асается оординат-
ных плосостей и центр сферы находится в той части простран-
ства, для аждой точи оторой x > 0, y < 0, z > 0 (посольу
в этой части расположена точа A(1; –1; 4)), то оординатами
центра являются (R; –R; R). С друой стороны, та а точа A
принадлежит сфере, то ее оординаты удовлетворяют уравне-
нию (16):
(1 – R)
2
+ (–1 + R)
2
+ (4 – R)
2
= R
2
,
отуда следует, что
R
2
– 6R + 9 = 0, или (R – 3)
2
= 0, т. е. R = 3.
Ответ.(x – 3)
2
+ (y + 3)
2
+ (z – 3)
2
= 9.
25. Вычислите расстояние от плосости 2x + 2y – z + 15 = 0
до сферы x
2
+ y
2
+ z
2
– 4 = 0.
26. Дана сфера x
2
+ y
2
+ z
2
– 25 = 0 и прямая l, проходящая
через точу A(2; 1; 1) параллельно ветору = {2; –4; –1}.
Найдите оординаты точе пересечения прямой l со сферой.
27. Найдите множество точе пространства, сумма вадра-
тов расстояний от аждой из оторых до двух данных точе
A(2; 3; –1) и B(1; –1; 3) имеет одно и то же значение m
2
.
x 7–
5
-------------
y 4–
1
-------------
z 5–
4
------------ -
a
