Cohen I.M., Kundu P.K. Fluid Mechanics
Подождите немного. Документ загружается.

552 Turbulence
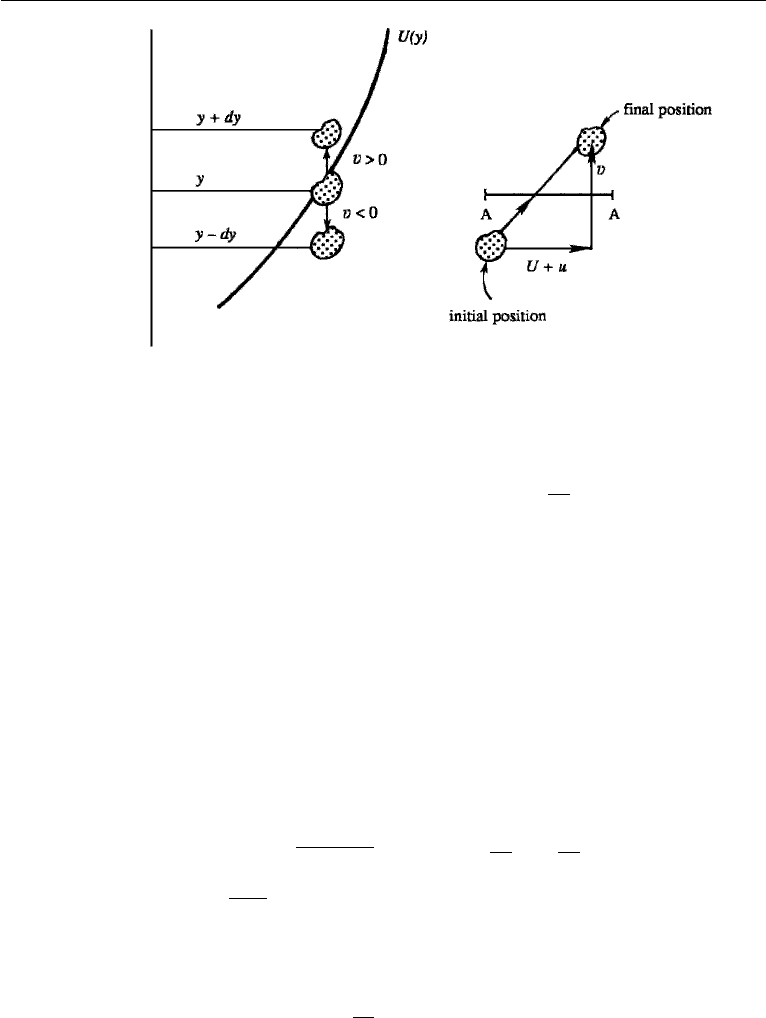
Figure 13.7 Movement of a particle in a turbulent shear flow.
after it has reached the level y +dy, and causes a negative u. Conversely, the particles
that travel downward (v < 0) tend to cause a positive u in the new level y − dy. On the
average, therefore, a positive v is mostly associated with a negative u, and a negative
v is mostly associated with a positive u. The correlation
uv is therefore negative for
the velocity field shown in Figure 13.7, where dU/dy > 0. This makes sense, since
in this case the x-momentum should tend to flow in the negative y-direction as the
turbulence tends to diffuse the gradients and decrease dU/dy.
The procedure of deriving equation (13.26) shows that the Reynolds stress arises
out of the nonlinear term ˜u
j
(∂ ˜u
i
/∂x
j
) of the equation of motion. It is a stress exerted
by the turbulent fluctuations on the mean flow. Another way to interpret the Reynolds
stress is that it is the rate of mean momentum transfer by turbulent fluctuations. Con-
sider again the shear flow U(y)shown in Figure 13.7, where the instantaneous velocity
is (U +u, v, w). The fluctuating velocity components constantly transport fluid par-
ticles, and associated momentum, across a plane AA normal to the y-direction. The
instantaneous rate of mass transfer across a unit area is ρ
0
v, and consequently the
instantaneous rate of x-momentum transfer is ρ
0
(U +u)v. Per unit area, the average
rate of flow of x-momentum in the y-direction is therefore
ρ
0
(U + u)v = ρ
0
U ¯v + ρ
0
uv = ρ
0
uv.
Generalizing, ρ
0
u
i
u
j
is the average flux of j-momentum along the i-direction, which
also equals the average flux of i-momentum along the j-direction.
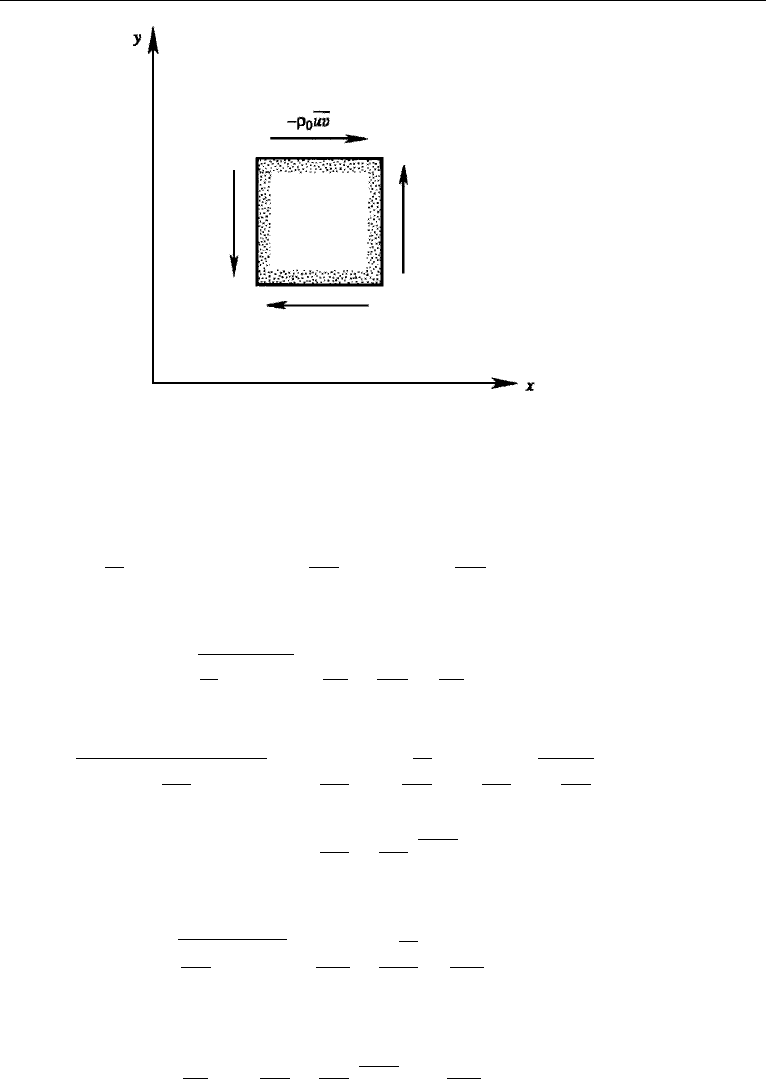
The sign convention for the Reynolds stress is the same as that explained in
Chapter 2, Section 4: On a surface whose outward normal points in the positive
x-direction, a positive τ
xy
points along the y-direction. According to this conven-
tion, the Reynolds stresses −ρ
0
uv on a rectangular element are directed as in Fig-
ure 13.8, if they are positive. The discussion in the preceding paragraph shows
that such a Reynolds stress causes a mean flow of x-momentum along the negative
y-direction.
5. Averaged Equations of Motion 553
Figure 13.8 Positive directions of Reynolds stresses on a rectangular element.
Mean Heat Equation
The heat equation (13.18) is
∂
∂t
(
¯
T + T
) + (U
j
+ u
j
)
∂
∂x
j
(
¯
T + T
) = κ
∂
2
∂x
2
j
(
¯
T + T
).
The average of the time derivative term is
∂
∂t
(
¯
T + T
) =
∂
¯
T
∂t
+
∂
¯
T
∂t
=
∂
¯
T
∂t
.
The average of the advective term is
(U
j
+ u
j
)
∂
∂x
j
(
¯
T + T
) = U
j
∂
¯
T
∂x
j
+ U
j
∂T
∂x
j
+¯u
j
∂
¯
T
∂x
j
+ u
j
∂T
∂x
j
= U
j
∂
¯
T
∂x
j
+
∂
∂x
j
(u
j
T
).
The average of the diffusion term is
∂
2
∂x
2
j
(
¯
T + T
) =
∂
2
¯
T
∂x
2
j
+
∂
2
T
∂x
2
j
=
∂
2
¯
T
∂x
2
j
.
Collecting terms, the mean heat equation takes the form
∂
¯
T
∂t
+ U
j
∂
¯
T
∂x
j
+
∂
∂x
j
(u
j
T
) = κ
∂
2
¯
T
∂x
2
j
,

554 Turbulence
which can be written as
D
¯
T
Dt
=
∂
∂x
j
κ
∂
¯
T
∂x
j
− u
j
T
. (13.27)
Multiplying by ρ
0
C
p
, we obtain
ρ
0
C
p
D
¯
T
Dt
=−
∂Q
j
∂x
j
, (13.28)
where the heat flux is given by
Q
j
=−k
∂
¯
T
∂x
j
+ ρ
0
C
p
u
j
T
, (13.29)
and k = ρ
0
C
p
κ is the thermal conductivity. Equation (13.29) shows that the fluctu-
ations cause an additional mean turbulent heat flux of ρ
0
C
p
uT
, in addition to the
molecular heat flux of −k∇
¯
T . For example, the surface of the earth becomes hot
during the day, resulting in a decrease of the mean temperature with height, and an
associated turbulent convective motion. An upward fluctuating motion is then mostly
associated with a positive temperature fluctuation, giving rise to an upward heat flux
ρ
0
C
p
wT
> 0.
6. Kinetic Energy Budget of Mean Flow
In this section we shall examine the sources and sinks of mean kinetic energy of a
turbulent flow. As shown in Chapter 4, Section 13, a kinetic energy equation can be
obtained by multiplying the equation for DU/Dt by U. The equation of motion for
the mean flow is, from equations (13.25) and (13.26),
∂U
i
∂t
+ U
j
∂U
i
∂x
j
=
1
ρ
0
∂ ¯τ
ij
∂x
j
−
g
ρ
0
¯ρδ
i3
, (13.30)
where the stress is given by
¯τ
ij
=−Pδ
ij
+ 2µE
ij
− ρ
0
u
i
u
j
. (13.31)
Here we have introduced the mean strain rate
E
ij
≡
1
2
∂U
i
∂x
j
+
∂U
j
∂x
i
.
Multiplying equation (13.30) by U
i
(and, of course, summing over i), we obtain
∂
∂t
1
2
U
2
i
+ U
j
∂
∂x
j
1
2
U
2
i
=
1
ρ
0
∂
∂x
j
(U
i
¯τ
ij
) −
1
ρ
0
¯τ
ij
∂U
i
∂x
j
−
g
ρ
0
¯ρU
i
δ
i3
.

6. Kinetic Energy Budget of Mean Flow 555
On introducing expression (13.31) for ¯τ
ij
, we obtain
D
Dt
1
2
U
2
i
=
∂
∂x
j
−
1
ρ
0
U
i
Pδ
ij
+ 2νU
i
E
ij
− u
i
u
j
U
i
+
1
ρ
0
Pδ
ij
∂U
i
∂x
j
− 2νE
ij
∂U
i
∂x
j
+ u
i
u
j
∂U
i
∂x
j
−
g
ρ
0
¯ρU
3
.
The fourth term on the right-hand side is proportional to δ
ij
(∂U
i
/∂x
j
) = ∂U
i
/∂x
i
=
0 by continuity. The mean kinetic energy balance then becomes
D
Dt
1
2
U
2
i
=
∂
∂x
j
−
PU
j
ρ
0
+ 2νU
i
E
ij
− u
i
u
j
U
i
transport
− 2νE
ij
E
ij
+ u
i
u
j
∂U
i
∂x
j
−
g
ρ
0
¯ρU
3
. (13.32)
viscous loss to loss to
dissipation turbulence potential
energy
The left-hand side represents the rate of change of mean kinetic energy, and the
right-hand side represents the various mechanisms that bring about this change. The
first three terms are in the “flux divergence” form. If equation (13.32) is integrated
over all space to obtain the rate of change of the total (or global) kinetic energy, then
the divergence terms can be transformed into a surface integral by Gauss’ theorem.
These terms then would not contribute if the flow is confined to a limited region in
space, with U = 0 at sufficient distance. It follows that the first three terms can only
transport or redistribute energy from one region to another, but cannot generate or
dissipate it. The first term represents the transport of mean kinetic energy by the mean
pressure, the second by the mean viscous stresses 2 νE
ij
, and the third by Reynolds
stresses.
The fourth term is the product of the mean strain rate E
ij
and the mean viscous
stress 2νE
ij
. It is a loss at every point in the flow and represents the direct viscous
dissipation of mean kinetic energy. The energy is lost to the agency that generates the
viscous stress, and so reappears as the kinetic energy of molecular motion (heat).
The fifth term is analogous to the fourth term. It can be written as
u
i
u
j
(∂U
i
/∂x
j
) = u
i
u
j
E
ij
, so that it is a product of the turbulent stress and the
mean strain rate field. (Note that the doubly contracted product of a symmetric tensor
u
i
u
j
and any tensor ∂U
i
/∂x
j
is equal to the product of u
i
u
j
and symmetric part of
∂U
i
/∂x
j
, namely, E
ij
; this is proved in Chapter 2, Section 11.) If the mean flow is
given by U(y), then
u
i
u
j
(∂U
i
/∂x
j
) = uv(dU/dy). We saw in the preceding section
that
uv is likely to be negative if dU/dy is positive. The fifth term
u
i
u
j
(∂U
i
/∂x
j
)
is therefore likely to be negative in shear flows. By analogy with the fourth term, it
must represent an energy loss to the agency that generates turbulent stress, namely the
fluctuating field. Indeed, we shall see in the following section that this term appears
on the right-hand side of an equation for the rate of change of turbulent kinetic energy,

556 Turbulence
but with the sign reversed. Therefore, this term generally results in a loss of mean
kinetic energy and a gain of turbulent kinetic energy. We shall call this term the shear
production of turbulence by the interaction of Reynolds stresses and the mean shear.
The sixth term represents the work done by gravity on the mean vertical motion.
For example, an upward mean motion results in a loss of mean kinetic energy, which
is accompanied by an increase in the potential energy of the mean field.
The two viscous terms in equation (13.32), namely, the viscous transport
2ν∂(U
i
E
ij
)/∂x
j
and the viscous dissipation −2νE
ij
E
ij
, are small in a fully turbulent
flow at high Reynolds numbers. Compare, for example, the viscous dissipation and
the shear production terms:
2νE
2
ij
u
i
u
j
(∂U
i
/∂x
j
)
∼
ν(U/L)
2
u
2
rms
U/L
∼
ν
UL
1,
where U is the scale for mean velocity, L is a length scale (for example, the width of
the boundary layer), and u
rms
is the rms value of the turbulent fluctuation; we have
also assumed that u
rms
and U are of the same order, since experiments show that
u
rms
is a substantial fraction of U . The direct influence of viscous terms is therefore
negligible on the mean kinetic energy budget. We shall see in the following section
that this is not true for the turbulent kinetic energy budget, in which the viscous terms
play a major role. What happens is the following: The mean flow loses energy to
the turbulent field by means of the shear production; the turbulent kinetic energy so
generated is then dissipated by viscosity.
7. Kinetic Energy Budget of Turbulent Flow
An equation for the turbulent kinetic energy is obtained by first finding an equation
for ∂u/∂t and taking the scalar product with u. The algebra becomes compact if we
use the “comma notation,” introduced in Chapter 2, Section 15, namely, that a comma
denotes a spatial derivative:
A
,i
≡
∂A
∂x
i
,
where A is any variable. (This notation is very simple and handy, but it may take a
little practice to get used to it. It is used in this book only if the algebra would become
cumbersome otherwise. There is only one other place in the book where this notation
has been applied, namely Section 5.7. With a little initial patience, the reader will
quickly see the convenience of this notation.)
Equations of motion for the total and mean flows are, respectively,
∂
∂t
(U
i
+ u
i
) + (U
j
+ u
j
)(U
i
+ u
i
)
,j
=−
1
ρ
0
(P + p)
,i
− g[1 − α(
¯
T + T
− T
0
)]δ
i3
+ ν(U
i
+ u
i
)
,jj
,
∂U
i
∂t
+ U
j
U
i,j
=−
1
ρ
0
P
,i
− g[1 − α(
¯
T − T
0
)]δ
i3
+ νU
i,jj
− (u
i
u
j
)
,j
.
7. Kinetic Energy Budget of Turbulent Flow 557
Subtracting, we obtain the equation of motion for the turbulent velocity u
i
:
∂u
i
∂t
+ U
j
u
i,j
+ u
j
U
i,j
+ u
j
u
i,j
− (u
i
u
j
)
,j
=−
1
ρ
0
p
,i
+ gαT
δ
i3
+ νu
i,jj
.
(13.33)
The equation for the turbulent kinetic energy is obtained by multiplying this equation
by u
i
and averaging.
The first two terms on the left-hand side of equation (13.33) give
u
i
∂u
i
∂t
=
∂
∂t
1
2
u
2
i
,
u
i
U
j
u
i,j
= U
j
1
2
u
2
i
,j
.
The third, fourth and fifth terms on the left-hand side of equation (13.33) give
u
i
u
j
U
i,j
= u
i
u
j
U
i,j
,
u
i
u
j
u
i,j
= (
1
2
u
2
i
u
j
)
,j
−
1
2
u
2
i
u
j,j
=
1
2
(u
2
i
u
j
)
,j
,
−u
i
(u
i
u
j
)
,j
=−¯u
i
(u
i
u
j
)
,j
= 0,
where we have used the continuity equation u
i,i
= 0 and ¯u
i
= 0.
The first and second terms on the right-hand side of equation (13.33) give
−u
i
1
ρ
0
p
,i
=−
1
ρ
0
(u
i
p)
,i
,
u
i
gαT
δ
i3
= gαwT
.
The last term on the right-hand side of equation (13.33) gives
ν
u
i
u
i,jj
= ν{u
i
u
i,jj
+
1
2
(u
i,j
+ u
j,i
)(u
i,j
− u
j,i
)},
where we have added the doubly contracted product of a symmetric tensor (u
i,j
+u
j,i
)
and an antisymmetric tensor (u
i,j
−u
j,i
), such a product being zero. In the first term
on the right-hand side, we can write u
i,jj
= (u
i,j
+u
j,i
)
,j
because of the continuity
equation. Then we can write
ν
u
i
u
i,jj
= ν{u
i
(u
i,j
+ u
j,i
)
,j
+ (u
i,j
+ u
j,i
)(u
i,j
−
1
2
u
i,j
−
1
2
u
j,i
)}
= ν{[
u
i
(u
i,j
+ u
j,i
)]
,j
−
1
2
(u
i,j
+ u
j,i
)
2
}.
Defining the fluctuating strain rate by
e
ij
≡
1
2
(u
i,j
+ u
j,i
),
558 Turbulence
we finally obtain
ν
u
i
u
i,jj
= 2ν[u
i
e
ij
]
,j
− 2νe
ij
e
ij
.
Collecting terms, the turbulent energy equation becomes
D
Dt
1
2
u
2
i
=−
∂
∂x
j
1
ρ
0
pu
j
+
1
2
u
2
i
u
j
− 2νu
i
e
ij
transport
− u
i
u
j
U
i,j
+ gαwT
− 2νe
ij
e
ij
. (13.34)
shear prod buoyant prod viscous diss
The first three terms on the right-hand side are in the flux divergence form and con-
sequently represent the spatial transport of turbulent kinetic energy. The first two
terms represent the transport by turbulence itself, whereas the third term is viscous
transport.
The fourth term
u
i
u
j
U
i,j
also appears in the kinetic energy budget of the
mean flow with its sign reversed, as seen by comparing equation (13.32) and equa-
tion (13.34). As argued in the preceding section, −
u
i
u
j
U
i,j
is usually positive, so
that this term represents a loss of mean kinetic energy and a gain of turbulent kinetic
energy. It must then represent the rate of generation of turbulent kinetic energy by the
interaction of the Reynolds stress with the mean shear U
i,j
. Therefore,
Shear production =−u
i
u
j
∂U
i
∂x
j
. (13.35)
The fifth term gα
wT
can have either sign, depending on the nature of the back-
ground temperature distribution
¯
T(z). In a stable situation in which the background
temperature increases upward (as found, e.g., in the atmospheric boundary layer at
night), rising fluid elements are likely to be associated with a negative temperature
fluctuation, resulting in
wT
< 0, which means a downward turbulent heat flux. In
such a stable situation gα
wT
represents the rate of turbulent energy loss by work-
ing against the stable background density gradient. In the opposite case, when the
background density profile is unstable, the turbulent heat flux
wT
is upward, and
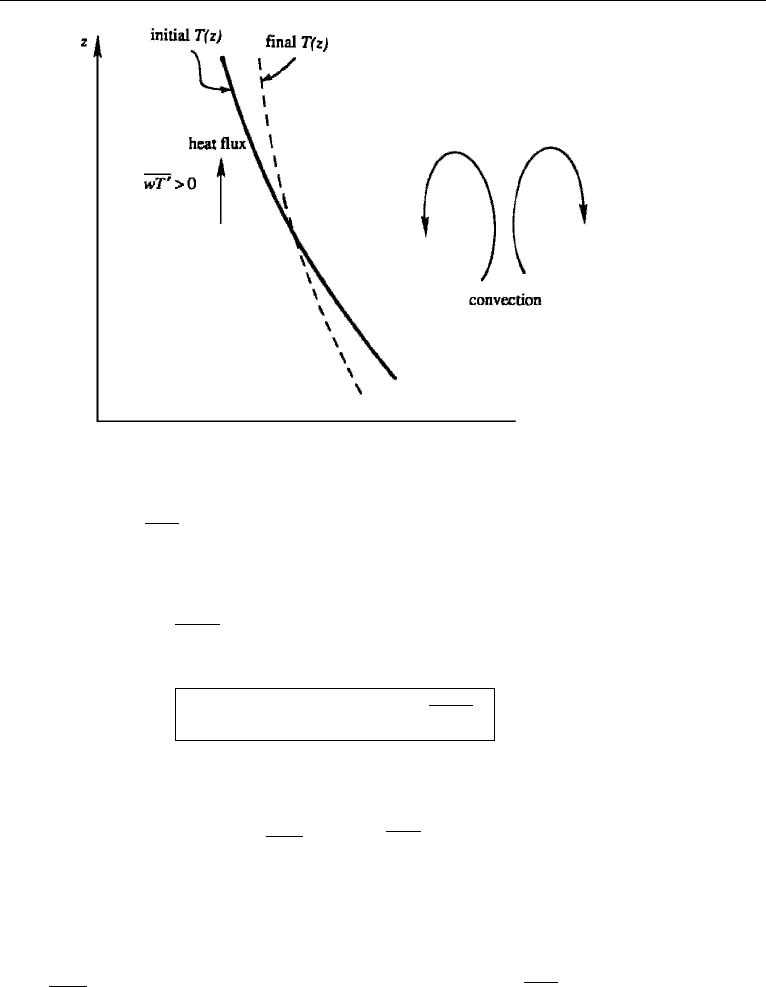
convective motions cause an increase of turbulent kinetic energy (Figure 13.9). We
shall call gα
wT
the buoyant production of turbulent kinetic energy, keeping in mind
that it can also be a buoyant “destruction” if the turbulent heat flux is downward.
Therefore,
Buoyant production = gαwT
. (13.36)
The buoyant generation of turbulent kinetic energy lowers the potential energy
of the mean field. This can be understood from Figure 13.9, where it is seen that the
heavier fluid has moved downward in the final state as a result of the heat flux. This
8. Turbulence Production and Cascade 559
Figure 13.9 Heat flux in an unstable environment, generating turbulent kinetic energy and lowering the
mean potential energy.
can also be demonstrated by deriving an equation for the mean potential energy, in
which the term gα
wT
appears with a negative sign on the right-hand side. Therefore,
the buoyant generation of turbulent kinetic energy by the upward heat flux occurs at
the expense of the mean potential energy. This is in contrast to the shear production
of turbulent kinetic energy, which occurs at the expense of the mean kinetic energy.
The sixth term 2ν
e
ij
e
ij
is the viscous dissipation of turbulent kinetic energy, and
is usually denoted by ε:
ε =Viscous dissipation = 2νe
ij
e
ij
. (13.37)
This term is not negligible in the turbulent kinetic energy equation, although an
analogous term (namely 2νE
2
ij
) is negligible in the mean kinetic energy equation, as
discussed in the preceding section. In fact, the viscous dissipation ε is of the order of
the turbulence production terms (
u
i
u
j
U
i,j
or gαwT
) in most locations.
8. Turbulence Production and Cascade
Evidence suggests that the large eddies in a turbulent flow are anisotropic, in the
sense that they are “aware” of the direction of mean shear or of background density
gradient. In a completely isotropic field the off-diagonal components of the Reynolds
stress
u
i
u
j
are zero (see Section 5 here), as is the upward heat flux wT
because there
is no preference between the upward and downward directions. In such an isotropic
case no turbulent energy can be extracted from the mean field. Therefore, turbulence
must develop anisotropy if it has to sustain itself against viscous dissipation.
A possible mechanism of generating anisotropy in a turbulent shear flow is dis-
cussed by Tennekes and Lumley (1972, p. 41). Consider a parallel shear flow U(y)
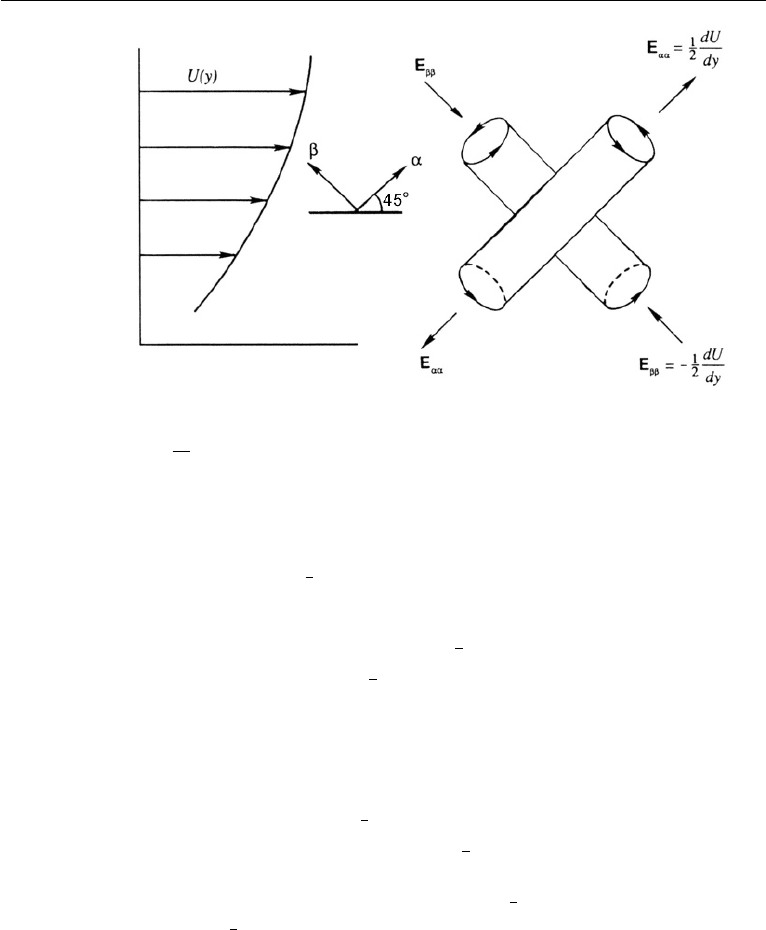
560 Turbulence
Figure 13.10 Large eddies oriented along the principal directions of a parallel shear flow. Note that the
vortex aligned with the α-axis has a positive v when u is negative and a negative v when u is positive,
resulting in
uv < 0.
shown in Figure 13.10, in which the fluid elements translate, rotate, and undergo
shearing deformation. The nature of deformation of an element depends on the ori-
entation of the element. An element oriented parallel to the xy-axes undergoes only
a shear strain rate E
xy
=
1
2
dU/dy, but no linear strain rate (E
xx
= E
yy
= 0). The
strain rate tensor in the xy-coordinate system is therefore
E =
0
1
2
dU/dy
1
2
dU/dy 0
.
As shown in Chapter 3, Section 10, such a symmetric tensor can be diagonalized by
rotating the coordinate system by 45
◦
. Along these principal axes (denoted by α and
β in Figure 13.10), the strain rate tensor is
E =
1
2
dU/dy 0
0 −
1
2
dU/dy
,
so that there is a linear extension rate of E
αα
=
1
2
dU/dy, a linear compression
rate of E
ββ
=−
1
2
dU/dy, and no shear (E
αβ
= 0). The kinematics of stretching and
compression along the principal directions in a parallel shear flow is discussed further
in Chapter 3, Section 10.
The large eddies with vorticity oriented along the α-axis intensify in strength due
to the vortex stretching, and the ones with vorticity oriented along the β-axis decay
in strength. The net effect of the mean shear on the turbulent field is therefore to
cause a predominance of eddies with vorticity oriented along the α-axis. As is evident
in Figure 13.10, these eddies are associated with a positive u when v is negative,

8. Turbulence Production and Cascade 561
and with a negative u when v is positive, resulting in a positive value for the shear
production −
uv(dU/dy).
The largest eddies are of order of the width of the shear flow, for example the
diameter of a pipe or the width of a boundary layer along a wall or along the upper
surface of the ocean. These eddies extract kinetic energy from the mean field. The
eddies that are somewhat smaller than these are strained by the velocity field of the
largest eddies, and extract energy from the larger eddies by the same mechanism of
vortex stretching. The much smaller eddies are essentially advected in the velocity
field of the large eddies, as the scales of the strain rate field of the large eddies are much
larger than the size of a small eddy. Therefore, the small eddies do not interact with
either the large eddies or the mean field. The kinetic energy is therefore cascaded
down from large to small eddies in a series of small steps. This process of energy
cascade is essentially inviscid, as the vortex stretching mechanism arises from the
nonlinear terms of the equations of motion.
In a fully turbulent shear flow (i.e., for large Reynolds numbers), therefore, the
viscosity of the fluid does not affect the shear production, if all other variables are
held constant. The viscosity does, however, determine the scales at which turbulent
energy is dissipated into heat. From the expression ε = 2ν
e
ij
e
ij
, it is clear that the
energy dissipation is effective only at very small scales, which have high fluctuating
strain rates. The continuous stretching and cascade generate long and thin filaments,
somewhat like “spaghetti.” When these filaments become thin enough, molecular
diffusive effects are able to smear out their velocity gradients. These are the small-
est scales in a turbulent flow and are responsible for the dissipation of the turbulent
kinetic energy. Figure 13.11 illustrates the deformation of a fluid particle in a tur-
bulent motion, suggesting that molecular effects can act on thin filaments generated
by continuous stretching. The large mixing rates in a turbulent flow, therefore, are
essentially a result of the turbulent fluctuations generating the large surfaces on which
the molecular diffusion finally acts.
It is clear that ε does not depend on ν, but is determined by the inviscid properties
of the large eddies, which supply the energy to the dissipating scales. Suppose l is
a typical length scale of the large eddies (which may be taken equal to the integral
length scale defined from a spatial correlation function, analogous to the integral time
scale defined by equation (13.10)), and u
is a typical scale of the fluctuating velocity
Figure 13.11 Successive deformations of a marked fluid element. Diffusive effects cause smearing when
the scale becomes of the order of the Kolmogorov microscale.
