Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

532 Instability

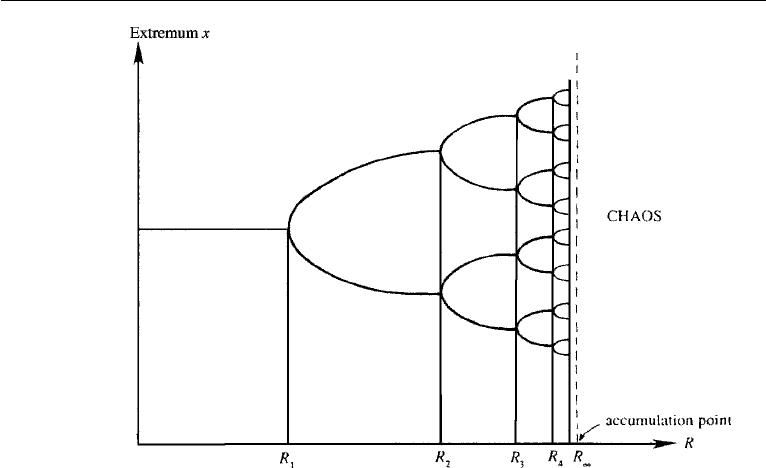
Figure 12.31 Bifurcation diagram during period doubling. The period doubles at each value R

of the

nonlinearity parameter. For large n the “bifurcation tree” becomes self similar. Chaos sets in beyond the

accumulation point R

∞

limit cycle with frequency ω

.AsR is increased, two more frequencies

(ω

and ω

) appear through additional bifurcations. In this scenario the ratios

of the three frequencies (such as ω

/ω

) are irrational numbers, so that the

motion consisting of the three frequencies is not exactly periodic. (When the

ratios are rational numbers, the motion is exactly periodic. To see this, think

of the Fourier series of a periodic function in which the various terms repre-

sent sinusoids of the fundamental frequency ω and its harmonics 2ω,3ω,....

Some of the Fourier coefﬁcients could be zero.) The spectrum for these sys-

tems suddenly develops broadband characteristics of chaotic motion as soon

as the third frequency ω

appears. The exact point at which chaos sets in is

not easy to detect in a measurement; in fact the third frequency may not be

identiﬁable in the spectrum before it becomes broadband. The Ruelle–Takens

theory is fundamentally different from that of Landau, who conjectured that

turbulence develops due to an inﬁnite number of bifurcations, each gener-

ating a new higher frequency, so that the spectrum becomes saturated with

peaks and resembles a continuous one. According to Berg´e, Pomeau, and

Vidal (1984), the B´enard convection experiments in water seem to suggest

that turbulence in this case probably sets in according to the Ruelle–Takens

scenario.

The development of chaos in the Lorenz attractor is more complicated and does

not follow either of the two routes mentioned in the preceding.

Exercises 533

Closure

Perhaps the most intriguing characteristic of a chaotic system is the extreme sensitivity

to initial conditions. That is, solutions with arbitrarily close initial conditions evolve

into two quite different states. Most nonlinear systems are susceptible to chaotic

behavior. The extreme sensitivity to initial conditions implies that nonlinear phe-

nomena (including the weather, in which Lorenz was primarily interested when he

studied the convection problem) are essentially unpredictable, no matter how well we

know the governing equations or the initial conditions. Although the subject of chaos

has become a scientiﬁc revolution recently, the central idea was conceived by Henri

Poincar´e in 1908. He did not, of course, have the computing facilities to demonstrate

it through numerical integration.

It is important to realize that the behavior of chaotic systems is not intrinsically

indeterministic; as such the implication of deterministic chaos is different from that of

the uncertainty principle of quantum mechanics. In any case, the extreme sensitivity

to initial conditions implies that the future is essentially unknowable because it is

never possible to know the initial conditions exactly. As discussed by Davies (1988),

this fact has interesting philosophical implications regarding the evolution of the

universe, including that of living species.

We have examined certain elementary ideas about how chaotic behavior may

result in simple nonlinear systems having only a small number of degrees of freedom.

Turbulence in a continuous ﬂuid medium is capable of displaying an inﬁnite number

of degrees of freedom, and it is unclear whether the study of chaos can throw a great

deal of light on more complicated transitions such as those in pipe or boundary layer

ﬂow. However, the fact that nonlinear systems can have chaotic solutions for a large

value of the nonlinearity parameter (see Figure 12.29 again) is an important result by

itself.

Exercises

1. Consider the thermal instability of a ﬂuid conﬁned between two rigid plates,

as discussed in Section 3. It was stated there without proof that the minimum critical

Rayleigh number of Ra

= 1708 is obtained for the gravest even mode. To verify

this, consider the gravest odd mode for which

W = A sin q

z + B sinh qz+ C sinh q

∗

(Compare this with the gravest even mode structure: W = A cos q

z + B cosh qz+

C cosh q

∗

z.) Following Chandrasekhar (1961, p. 39), show that the minimum

Rayleigh number is now 17,610, reached at the wavenumber K

= 5.365.

2. Consider the centrifugal instability problem of Section 5. Making the

narrow-gap approximation, work out the algebra of going from equation (12.37)

to equation (12.38).

3. Consider the centrifugal instability problem of Section 5. From equa-

tions (12.38) and (12.40), the eigenvalue problem for determining the marginal

534 Instability

state (σ = 0) is

− k

)

ˆu

= (1 + αx) ˆu

, (12.87)

− k

)

ˆu

=−Ta k

ˆu

, (12.88)

with ˆu

= D ˆu

=ˆu

= 0atx = 0 and 1. Conditions on ˆu

are satisﬁed by assuming

solutions of the form

ˆu

∞



m=1

sin mπx. (12.89)

Inserting this in equation (12.87), obtain an equation for ˆu

, and arrange so that the

solution satisﬁes the four remaining conditions on ˆu

. With ˆu

determined in this

manner and ˆu

given by equation (12.89), equation (12.88) leads to an eigenvalue

problem for Ta(k). Following Chandrasekhar (1961, p. 300), show that the minimum

Taylor number is given by equation (12.41) and is reached at k

= 3.12.

4. Consider an inﬁnitely deep ﬂuid of density ρ

lying over an inﬁnitely deep

ﬂuid of density ρ

>ρ

. By setting U

= U

= 0, equation (12.51) shows that

c =



− ρ

+ ρ

. (12.90)

Argue that if the whole system is given an upward vertical acceleration a, then g in

equation (12.90) is replaced by g



= g +a. It follows that there is instability if g



< 0,

that is, the system is given a downward acceleration of magnitude larger than g. This

is called the Rayleigh–Taylor instability, which can be observed simply by rapidly

accelerating a beaker of water downward.

5. Consider the inviscid instability of parallel ﬂows given by the Rayleigh

equation

(U − c)(ˆv

− k

ˆv) − U

ˆv = 0, (12.91)

where the y-component of the perturbation velocity is v =ˆv exp(i kx − ikct).

(i) Note that this equation is identical to the Rayleigh equation (12.76) written in

terms of the stream function amplitude φ, as it must because ˆv =−ikφ.For

a ﬂow bounded by walls at y

and y

, note that the boundary conditions are

identical in terms of φ and ˆv.

(ii) Show that if c is an eigenvalue of equation (12.91), then so is its conjugate

∗

= c

− ic

. What aspect of equation (12.91) allows the result to be valid?

(iii) Let U(y)be an antisymmetric jet, so that U(y) =−U(−y). Demonstrate that

if c(k) is an eigenvalue, then −c(k) is also an eigenvalue. Explain the result

physically in terms of the possible directions of propagation of perturbations

in an antisymmetric ﬂow.

(iv) Let U(y) be a symmetric jet. Show that in this case ˆv is either symmetric or

antisymmetric about y = 0.

Literature Cited 535

[Hint: Letting y →−y, show that the solution ˆv(−y) satisﬁes equation (12.91)

with the same eigenvalue c. Form a symmetric solution S( y) =ˆv( y) +ˆv(−y) =

S(−y), and an antisymmetric solution A( y) =ˆv( y)−ˆv(−y) =−A(−y). Then write

A[S-eqn]−S[A-eqn]=0, where S-eqn indicates the differential equation (12.91)

in terms of S. Canceling terms this reduces to (SA



− AS



)



= 0, where the prime

(



) indicates y-derivative. Integration gives SA



− AS



= 0, where the constant of

integration is zero because of the boundary condition. Another integration gives S =

bA, where b is a constant of integration. Because the symmetric and antisymmetric

functions cannot be proportional, it follows that one of them must be zero.]

Comments:Ifv is symmetric, then the cross-stream velocity has the same sign

across the entire jet, although the sign alternates every half of a wavelength along the

jet. This mode is consequently called sinuous. On the other hand, if v is antisymmetric,

then the shape of the jet expands and contracts along the length. This mode is now

generally called the sausage instability because it resembles a line of linked sausages.

6. For a Kelvin–Helmholtz instability in a continuously stratiﬁed ocean, obtain

a globally integrated energy equation in the form



+ w

+ g

/ρ

)dV =−



uwU

dV.

(As in Figure 12.25, the integration in x takes place over an integral number

of wavelengths.) Discuss the physical meaning of each term and the mechanism of

instability.

Literature Cited

Bayly, B. J., S.A. Orszag, and T. Herbert (1988). “Instability mechanisms in shear-ﬂow transition.” Annual

Review of Fluid Mechanics 20: 359–391.

Berg´e, P., Y. Pomeau, and C. Vidal (1984). Order Within Chaos, New York: Wiley.

Bhattacharya, P., M. P. Manoharan, R. Govindarajan, and R. Narasimha (2006). “The critical Reynolds

number of a laminar incompressible mixing layer from minimal composite theory.” Journal of Fluid

Mechanics 565: 105–114.

Chandrasekhar, S. (1961). Hydrodynamic and Hydromagnetic Stability, London: Oxford University Press;

New York: Dover reprint, 1981.

Coles, D. (1965). “Transition in circular Couette ﬂow.” Journal of Fluid Mechanics 21: 385–425.

Davies, P. (1988). Cosmic Blueprint, New York: Simon and Schuster.

Drazin, P. G. and W. H. Reid (1981). Hydrodynamic Stability, London: Cambridge University Press.

Eckhardt, B., T. M. Schneider, B. Hof, and J. Westerweel (2007). “Turbulence transition in pipe ﬂow.”

Annual Review of Fluid Mechanics 39: 447–468.

Eriksen, C. C. (1978). “Measurements and models of ﬁne structure, internal gravity waves, and wave

breaking in the deep ocean.” Journal of Geophysical Research 83: 2989–3009.

Feigenbaum, M. J. (1978). “Quantitative universality for a class of nonlinear transformations.” Journal of

Statistical Physics 19: 25–52.

Fransson, J. H. M. and P. H. Alfredsson (2003). “On the disturbance growth in an asymptotic suction

boundary layer.” Journal of Fluid Mechanics 482: 51–90.

Grabowski, W. J. (1980). “Nonparallel stability analysis of axisymmetric stagnation point ﬂow.” Physics

of Fluids 23: 1954–1960.

Heisenberg, W. (1924). “

Uber Stabilit¨at und Turbulenz von Fl¨ussigkeitsstr¨omen.” Annalen der Physik

(Leipzig) (4) 74: 577–627.

536 Instability

Howard, L. N. (1961). “Note on a paper of John W. Miles.” Journal of Fluid Mechanics 13: 158–160.

Huppert, H. E. and J. S. Turner (1981). “Double-diffusive convection.” Journal of Fluid Mechanics 106:

299–329.

Klebanoff, P. S., K. D. Tidstrom, and L. H. Sargent (1962). “The three-dimensional nature of boundary

layer instability”. Journal of Fluid Mechanics 12: 1–34.

Lanford, O. E. (1982). “The strange attractor theory of turbulence.” Annual Review of Fluid Mechanics

14: 347–364.

Lin, C. C. (1955). The Theory of Hydrodynamic Stability, London: Cambridge University Press, Chapter 8.

Lorenz, E. (1963). “Deterministic nonperiodic ﬂows.” Journal of Atmospheric Sciences 20:

130–141.

Miles, J. W. (1961). “On the stability of heterogeneous shear ﬂows.” Journal of Fluid Mechanics 10:

496–508.

Miles, J. W. (1986). “Richardson’s criterion for the stability of stratiﬁed ﬂow.” Physics of Fluids 29:

3470–3471.

Nayfeh, A. H. and W. S. Saric (1975). “Nonparallel stability of boundary layer ﬂows.” Physics of Fluids

18: 945–950.

Reshotko, E. (2001). “Transient growth: A factor in bypass transition.” Physics of Fluids 13: 1067–1075.

Ruelle, D. and F. Takens (1971). “On the nature of turbulence.” Communications in Mathematical Physics

20: 167–192.

Scotti, R. S. and G. M. Corcos (1972). “An experiment on the stability of small disturbances in a stratiﬁed

free shear layer.” Journal of Fluid Mechanics 52: 499–528.

Shen, S. F. (1954). “Calculated ampliﬁed oscillations in plane Poiseuille and Blasius Flows.” Journal of

the Aeronautical Sciences 21: 62–64.

Stern, M. E. (1960). “The salt fountain and thermohaline convection.” Tellus 12: 172–175.

Stommel, H., A. B. Arons, and D. Blanchard (1956). “An oceanographic curiosity: The perpetual salt

fountain.” Deep-Sea Research 3: 152–153.

Thorpe, S. A. (1971). “Experiments on the instability of stratiﬁed shear ﬂows: Miscible ﬂuids.” Journal of

Fluid Mechanics 46: 299–319.

Turner, J. S. (1973). Buoyancy Effects in Fluids, London: Cambridge University Press.

Turner, J. S. (1985). “Convection in multicomponent systems.” Naturwissenschaften 72: 70–75.

Woods, J. D. (1969). “On Richardson’s number as a criterion for turbulent–laminar transition in the atmo-

sphere and ocean.” Radio Science 4: 1289–1298.

Yih, C. S. (1979). Fluid Mechanics: A Concise Introduction to the Theory, Ann Arbor, MI: West River

Press, pp. 469–496.

Chapter 13

Turbulence

1. Introduction ........................ 537

2. Historical Notes ..................... 539

3. Averages ............................ 541

4. Correlations and Spectra ............ 543

5. Averaged Equations of Motion ....... 547

Mean Continuity Equation ........... 548

Mean Momentum Equation .......... 549

Reynolds Stress ..................... 550

Mean Heat Equation ................ 553

6. Kinetic Energy Budget of

Mean Flow .......................... 554

7. Kinetic Energy Budget of

Turbulent Flow...................... 556

8. Turbulence Production and

Cascade ............................ 559

9. Spectrum of Turbulence in Inertial

Subrange ........................... 562

10. Wall-Free Shear Flow................ 564

Intermittency ....................... 565

Entrainment ........................ 566

Self-Preservation .................... 566

Consequence of Self-Preservation in

a Plane Jet ....................... 567

Turbulent Kinetic Energy Budget in

aJet............................. 568

11. Wall-Bounded Shear Flow ........... 570

Inner Layer: Law of the Wall ........ 571

Outer Layer: Velocity Defect Law .... 573

Overlap Layer: Logarithmic Law .... 573

Rough Surface ...................... 579

Variation of Turbulent Intensity ...... 580

12. Eddy Viscosity and Mixing

Length.............................. 580

13. Coherent Structures in

a Wall Layer ........................ 584

14. Turbulence in a Stratiﬁed

Medium............................. 586

The Richardson Numbers ............ 587

Monin–Obukhov Length ............. 588

Spectrum of Temperature

Fluctuations...................... 589

15. Taylor’s Theory of Turbulent

Dispersion .......................... 591

Rate of Dispersion of a Single

Particle .......................... 591

Random Walk ....................... 595

Behavior of a Smoke Plume in

theWind......................... 596

Effective Diffusivity ................. 597

16. Concluding Remarks................. 598

Exercises............................ 598

Literature Cited ..................... 600

Supplemental Reading .............. 601

1. Introduction

Most ﬂows encountered in engineering practice and in nature are turbulent. The

boundary layer on an aircraft wing is likely to be turbulent, the atmospheric boundary

layer over the earth’s surface is turbulent, and the major oceanic currents are turbu-

lent. In this chapter we shall discuss certain elementary ideas about the dynamics of

537

DOI: 10.1016/B978-0-12-381399-2.50013-7

538 Turbulence

turbulent ﬂows. We shall see that such ﬂows do not allow a strict analytical study, and

one depends heavily on physical intuition and dimensional arguments. In spite of our

everyday experience with it, turbulence is not easy to deﬁne precisely. In fact, there

is a tendency to confuse turbulent ﬂows with “random ﬂows.” With some humor,

Lesieur (1987) said that “turbulence is a dangerous topic which is at the origin of

serious ﬁghts in scientiﬁc meetings since it represents extremely different points of

view, all of which have in common their complexity, as well as an inability to solve

the problem. It is even difﬁcult to agree on what exactly is the problem to be solved.”

Some characteristics of turbulent ﬂows are the following:

(1) Randomness: Turbulent ﬂows seem irregular, chaotic, and unpredictable.

(2) Nonlinearity: Turbulent ﬂows are highly nonlinear. The nonlinearity serves

two purposes. First, it causes the relevant nonlinearity parameter, say the

Reynolds number Re, the Rayleigh number Ra, or the inverse Richardson num-

ber Ri

−1

, to exceed a critical value. In unstable ﬂows small perturbations grow

spontaneously and frequently equilibrate as ﬁnite amplitude disturbances. On

further exceeding the stability criteria, the new state can become unstable to

more complicated disturbances, and the ﬂow eventually reaches a chaotic state.

Second, the nonlinearity of a turbulent ﬂow results in vortex stretching, a key

process by which three-dimensional turbulent ﬂows maintain their vorticity.

(3) Diffusivity: Due to the macroscopic mixing of ﬂuid particles, turbulent ﬂows

are characterized by a rapid rate of diffusion of momentum and heat.

(4) Vorticity: Turbulence is characterized by high levels of ﬂuctuating vorticity.

The identiﬁable structures in a turbulent ﬂow are vaguely called eddies. Flow

visualization of turbulent ﬂows shows various structures—coalescing, divid-

ing, stretching, and above all spinning. A characteristic feature of turbulence is

the existence of an enormous range of eddy sizes. The large eddies have a size

of order of the width of the region of turbulent ﬂow; in a boundary layer this is

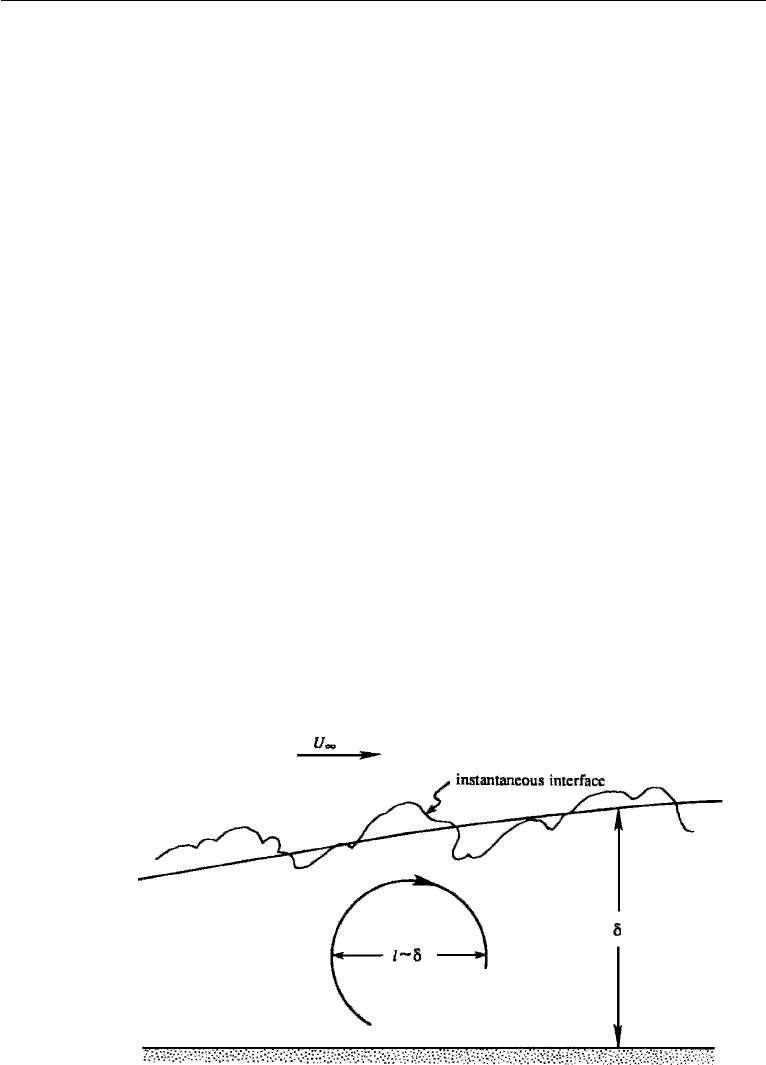
the thickness of the layer (Figure 13.1). The large eddies contain most of the

Figure 13.1 Turbulent ﬂow in a boundary layer, showing that a large eddy has a size of the order of

boundary layer thickness.

2. Historical Notes 539

energy. The energy is handed down from large to small eddies by nonlinear

interactions, until it is dissipated by viscous diffusion in the smallest eddies,

whose size is of the order of millimeters.

(5) Dissipation: The vortex stretching mechanism transfers energy and vorticity

to increasingly smaller scales, until the gradients become so large that they are

smeared out (i.e., dissipated) by viscosity. Turbulent ﬂows therefore require a

continuous supply of energy to make up for the viscous losses.

These features of turbulence suggest that many ﬂows that seem “random,” such

as gravity waves in the ocean or the atmosphere, are not turbulent because they are

not dissipative, vortical, and nonlinear.

Incompressible turbulent ﬂows in systems not large enough to be inﬂuenced by

the Coriolis force will be studied in this chapter. These ﬂows are three-dimensional. In

large-scale geophysical systems, on the other hand, the existence of stratiﬁcation and

Coriolis force severely restricts vertical motion and leads to a chaotic ﬂow that is nearly

“geostropic” and two-dimensional. Geostrophic turbulence is brieﬂy commented on

in Chapter 14.

2. Historical Notes

Turbulence research is currently at the forefront of modern ﬂuid dynamics, and some

of the well-known physicists of this century have worked in this area. Among them

are G. I. Taylor, Kolmogorov, Reynolds, Prandtl, von Karman, Heisenberg, Landau,

Millikan, and Onsagar. A brief historical outline is given in what follows; further

interesting details can be found in Monin and Yaglom (1971). The reader is expected

to fully appreciate these historical remarks only after reading the chapter.

The ﬁrst systematic work on turbulence was carried out by Osborne Reynolds

in 1883. His experiments in pipe ﬂows, discussed in Section 9.1, showed that the

ﬂow becomes turbulent or irregular when the nondimensional ratio Re = UL/ν,

later named the Reynolds number by Sommerfeld, exceeds a certain critical value.

(Here ν is the kinematic viscosity, U is the velocity scale, and L is the length scale.)

This nondimensional number subsequently proved to be the parameter that deter-

mines the dynamic similarity of viscous ﬂows. Reynolds also separated turbulent

variables as the sum of a mean and a ﬂuctuation and arrived at the concept of tur-

bulent stress. The discovery of the signiﬁcance of Reynolds number and turbulent

stress has proved to be of fundamental importance in our present knowledge of

turbulence.

In 1921 the British physicist G. I. Taylor, in a simple and elegant study of

turbulent diffusion, introduced the idea of a correlation function. He showed that the

rms distance of a particle from its source point initially increases with time as ∝ t,

and subsequently as ∝

√

t, as in a random walk. Taylor continued his outstanding

work in a series of papers during 1935–1936 in which he laid down the foundation

of the statistical theory of turbulence. Among the concepts he introduced were those

of homogeneous and isotropic turbulence and of turbulence spectrum. Although real

turbulent ﬂows are not isotropic (the turbulent stresses, in fact, vanish for isotropic

ﬂows), the mathematical techniques involved have proved valuable for describing the

540 Turbulence

small scales of turbulence, which are isotropic. In 1915 Taylor also introduced the

idea of mixing length, although it is generally credited to Prandtl for making full use of

the idea.

During the 1920s Prandtl and his student von Karman, working in G¨ottingen,

Germany, developed the semiempirical theories of turbulence. The most successful

of these was the mixing length theory, which is based on an analogy with the concept

of mean free path in the kinetic theory of gases. By guessing at the correct form for the

mixing length, Prandtl was able to deduce that the velocity proﬁle near a solid wall is

logarithmic, one of the most reliable results of turbulent ﬂows. It is for this reason that

subsequent textbooks on ﬂuid mechanics have for a long time gloriﬁed the mixing

length theory. Recently, however, it has become clear that the mixing length theory is

not helpful since there is really no rational way of predicting the form of the mixing

length. In fact, the logarithmic law can be justiﬁed from dimensional considerations

alone.

Some very important work was done by the British meteorologist Lewis

Richardson. In 1922 he wrote the very ﬁrst book on numerical weather prediction.

In this book he proposed that the turbulent kinetic energy is transferred from large

to small eddies, until it is destroyed by viscous dissipation. This idea of a spectral

energy cascade is at the heart of our present understanding of turbulent ﬂows. How-

ever, Richardson’s work was largely ignored at the time, and it was not until some

20 years later that the idea of a spectral cascade took a quantitative shape in the hands

of Kolmogorov and Obukhov in Russia. Richardson also did another important piece

of work that displayed his amazing physical intuition. On the basis of experimental

data on the movement of balloons in the atmosphere, he proposed that the effective

diffusion coefﬁcient of a patch of turbulence is proportional to l

4/3

, where l is the scale

of the patch. This is called Richardson’s four-third law, which has been subsequently

found to be in agreement with Kolmogorov’s ﬁve-third law of spectrum.

The Russian mathematician Kolmogorov, generally regarded as the greatest

probabilist of the twentieth century, followed up on Richardson’s idea of a spectral

energy cascade. He hypothesized that the statistics of small scales are isotropic and

depend on only two parameters, namely viscosity ν and the rate of dissipation ε.On

dimensional grounds, he derived that the smallest scales must be of size η = (ν

/ε)

1/4

His second hypothesis was that, at scales much smaller than l and much larger than

η, there must exist an inertial subrange in which ν plays no role; in this range the

statistics depend only on a single parameter ε. Using this idea, in 1941 Kolmogorov

and Obukhov independently derived that the spectrum in the inertial subrange must

be proportional to ε

2/3

−5/3

, where K is the wavenumber. The ﬁve-third law is

one of the most important results of turbulence theory and is in agreement with

observations.

There has been much progress in recent years in both theory and observations.

Among these may be mentioned the experimental work on the coherent structures

near a solid wall. Observations in the ocean and the atmosphere (which von

Karman called “a giant laboratory for turbulence research”), in which the Reynolds

numbers are very large, are shedding new light on the structure of stratiﬁed

turbulence.

3. Averages 541

3. Averages

The variables in a turbulent ﬂow are not deterministic in details and have to be treated

as stochastic or random variables. In this section we shall introduce certain deﬁnitions

and nomenclature used in the theory of random variables.

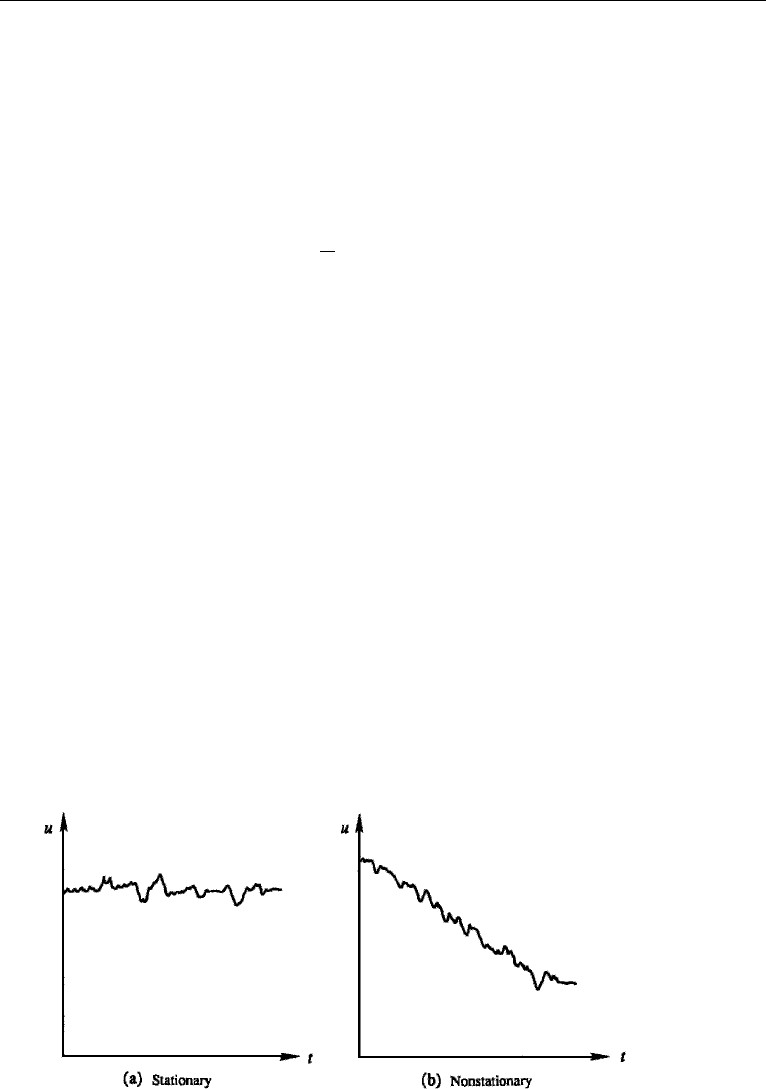
Let u(t ) be any measured variable in a turbulent ﬂow. Consider ﬁrst the case

when the “average characteristics” of u(t) do not vary with time (Figure 13.2a). In

such a case we can deﬁne the average variable as the time mean

¯u ≡ lim

→∞



u(t) dt. (13.1)

Now consider a situation in which the average characteristics do vary with time. An

example is the decaying series shown in Figure 13.2b, which could represent the

velocity of a jet as the pressure in the supply tank falls. In this case the average is a

function of time and cannot be formally deﬁned by using equation (13.1), because we

cannot specify how large the averaging interval t

should be made in evaluating the

integral (13.1). If we take t

to be very large then we may not get a “local” average,

and if we take t

to be very small then we may not get a reliable average. In such

a case, however, one can still deﬁne an average by performing a large number of

experiments, conducted under identical conditions. To deﬁne this average precisely,

we ﬁrst need to introduce certain terminology.

A collection of experiments, performed under an identical set of experimental

conditions, is called an ensemble, and an average over the collection is called an

ensemble average,orexpected value. Figure 13.3 shows an example of several records

of a random variable, for example, the velocity in the atmospheric boundary layer

measured from 8 am to 10 am in the morning. Each record is measured at the same

place, supposedly under identical conditions, on different days. The ith record is

denoted by u

(t). (Here the superscript does not stand for power.) All records in the

ﬁgure show that for some dynamic reason the velocity is decaying with time. In other

words, the expected velocity at 8 am is larger than that at 10 am. It is clear that the

average velocity at 9 am can be found by adding together the velocity at 9 am for

Figure 13.2 Stationary and nonstationary time series.