Cohen I.M., Kundu P.K. Fluid Mechanics
Подождите немного. Документ загружается.

502 Instability
The continuity equation can be satisfied by defining a streamfunction through
u =
∂ψ
∂z
,w=−
∂ψ
∂x
.
Equations (12.52) and (12.53) then become
ψ
zt
− ψ
x
U
z
+ ψ
xz
U =−
1
ρ
0
p
x
,
−ψ
xt
− ψ
xx
U =−
gρ
ρ
0
−
1
ρ
0
p
z
,
ρ
t
+ Uρ
x
+
ρ
0
N
2
g
ψ
x
= 0,
(12.54)
where subscripts denote partial derivatives.
As the coefficients of equation (12.54) are independent of x and t, exponential
variations in these variables are allowed. Consequently, we assume normal mode
solutions of the form
[ρ,p,ψ]=[ˆρ(z), ˆp(z),
ˆ
ψ(z)] e
ik(x−ct)
,
where quantities denoted by ( ˆ) are complex amplitudes. Because the flow is
unbounded in x, the wavenumber k must be real. The eigenvalue c = c
r
+ic
i
can be
complex, and the solution is unstable if there exists a c
i
> 0. Substituting the normal
modes, equation (12.54) becomes
(U − c)
ˆ
ψ
z
− U
z
ˆ
ψ =−
1
ρ
0
ˆp, (12.55)
k
2
(U − c)
ˆ
ψ =−
g ˆρ
ρ
0
−
1
ρ
0
ˆp
z
, (12.56)
(U − c) ˆρ +
ρ
0
N
2
g
ˆ
ψ = 0. (12.57)
We want to obtain a single equation in
ˆ
ψ. The pressure can be eliminated by
taking the z-derivative of equation (12.55) and subtracting equation (12.56). The
density can be eliminated by equation (12.57). This gives
(U − c)
d
2
dz
2
− k
2
ˆ
ψ −U
zz
ˆ
ψ +
N
2
U − c
ˆ
ψ = 0. (12.58)
This is the Taylor–Goldstein equation, which governs the behavior of perturbations
in a stratified parallel flow. Note that the complex conjugate of the equation is also
a valid equation because we can take the imaginary part of the equation, change the
sign, and add to the real part of the equation. Now because the Taylor–Goldstein
equation does not involve any i, a complex conjugate of the equation shows that if
ˆ
ψ
is an eigenfunction with eigenvalue c for some k, then
ˆ
ψ
∗
is a possible eigenfunction
with eigenvalue c
∗
for the same k. Therefore, to each eigenvalue with a positive c
i
there

7. Instability of Continuously Stratified Parallel Flows 503
is a corresponding eigenvalue with a negative c
i
. In other words, to each growing mode
there is a corresponding decaying mode. A nonzero c
i
therefore ensures instability.
The boundary conditions are that w = 0 on rigid boundaries at z = 0, d. This
requires ψ
x
= ik
ˆ
ψ exp(ikx − ikct) = 0 at the walls, which is possible only if
ˆ
ψ(0) =
ˆ
ψ(d) = 0. (12.59)
Richardson Number Criterion
A necessary condition for linear instability of inviscid stratified parallel flows can be
derived by defining a new variable φ by
φ ≡
ˆ
ψ
√
U − c
or
ˆ
ψ = (U − c)
1/2
φ.
Then we obtain the derivatives
ˆ
ψ
z
= (U − c)
1/2
φ
z
+
φU
z
2(U − c)
1/2
,
ˆ
ψ
zz
= (U − c)
1/2
φ
zz
+
U
z
φ
z
+ (1/2)φU
zz
(U − c)
1/2
−
1
4
φU
2
z
(U − c)
3/2
.
The Taylor–Goldstein equation then becomes, after some rearrangement,
d
dz
{(U − c)φ
z
}−
k
2
(U − c) +
1
2
U
zz
+
(1/4)U
2
z
− N
2
U − c
φ = 0. (12.60)
Now multiply equation (12.60) by φ
∗
(the complex conjugate of φ), integrate from
z = 0toz = d, and use the boundary conditions φ(0) = φ(d) = 0. The first term
gives
d
dz
{(U − c)φ
z
}φ
∗
dz =
d
dz
{(U − c)φ
z
φ
∗
}−(U − c)φ
z
φ
∗
z
dz
=−
(U − c)|φ
z
|
2
dz,
where we have used φ = 0 at the boundaries. Integrals of the other terms in equa-
tion (12.60) are also simple to manipulate. We finally obtain
N
2
− (1/4 )U
2
z
U − c
|φ|
2
dz =
(U − c){|φ
z
|
2
+ k
2
|φ|
2
} dz
+
1
2
U
zz
|φ|
2
dz. (12.61)
The last term in the preceding is real. The imaginary part of the first term can be found
by noting that
1
U − c
=
U − c
∗
|U − c|
2
=
U − c
r
+ ic
i
|U − c|
2
.

504 Instability
Then the imaginary part of equation (12.61) gives
c
i
N
2
− (1/4 )U
2
z
|U − c|
2
|φ|
2
dz =−c
i
{|φ
z
|
2
+ k
2
|φ|
2
} dz.
The integral on the right-hand side is positive. If the flow is such that N
2
>U
2
z
/4
everywhere, then the preceding equation states that c
i
times a positive quantity equals
c
i
times a negative quantity; this is impossible and requires that c
i
= 0 for such a
case. Defining the gradient Richardson number
Ri(z) ≡
N
2
U
2
z
, (12.62)
we can say that linear stability is guaranteed if the inequality
Ri >
1
4
(stable), (12.63)
is satisfied everywhere in the flow.
Note that the criterion does not state that the flow is necessarily unstable if
Ri <
1
4
somewhere, or even everywhere, in the flow. Thus Ri <
1
4
is a necessary
but not sufficient condition for instability. For example, in a jetlike velocity profile
u ∝ sech
2
z and an exponential density profile, the flow does not become unstable until
the Richardson number falls below 0.214. A critical Richardson number lower than
1
4
is also found in the presence of boundaries, which stabilize the flow. In fact, there is no
unique critical Richardson number that applies to all distributions of U(z) and N(z).
However, several calculations show that in many shear layers (having linear, tanh,
or error function profiles for velocity and density) the flow does become unstable to
disturbances of certain wavelengths if the minimum value of Ri in the flow (which is
generally at the center of the shear layer) is less than
1
4
. The “most unstable” wave,
defined as the first to become unstable as Ri is reduced below
1
4
, is found to have a
wavelength λ 7h, where h is the thickness of the shear layer. Laboratory (Scotti
and Corcos, 1972) as well as geophysical observations (Eriksen, 1978) show that the
requirement
Ri
min
<
1
4
,
is a useful guide for the prediction of instability of a stratified shear layer.
Howard’s Semicircle Theorem
A useful result concerning the behavior of the complex phase speed c in an inviscid
parallel shear flow, valid both with and without stratification, was derived by Howard
(1961). To derive this, first substitute
F ≡
ˆ
ψ
U − c
,

7. Instability of Continuously Stratified Parallel Flows 505
in the Taylor–Goldstein equation (12.58). With the derivatives
ˆ
ψ
z
= (U − c)F
z
+ U
z
F,
ˆ
ψ
zz
= (U − c)F
zz
+ 2U
z
F
z
+ U
zz
F,
Equation (12.58) gives
(U − c)[(U − c)F
zz
+ 2U
z
F
z
− k
2
(U − c)F ]+N
2
F = 0,
where terms involving U
zz
have canceled out. This can be rearranged in the form
d
dz
[(U − c)
2
F
z
]−k
2
(U − c)
2
F + N
2
F = 0.
Multiplying by F
∗
, integrating (by parts if necessary) over the depth of flow, and
using the boundary conditions, we obtain
−
(U − c)
2
F
z
F
∗
z
dz − k
2
(U − c)
2
|F |
2
dz +
N
2
|F |
2
dz = 0,
which can be written as
(U − c)
2
Qdz =
N
2
|F |
2
dz,
where
Q ≡|F
z
|
2
+ k
2
|F |
2
,
is positive. Equating real and imaginary parts, we obtain
[(U − c
r
)
2
− c
2
i
]Qdz =
N
2
|F |
2
dz, (12.64)
c
i
(U − c
r
)Q dz = 0. (12.65)
For instability c
i
= 0, for which equation (12.65) shows that (U − c
r
) must change
sign somewhere in the flow, that is,
U
min
<c
r
<U
max
, (12.66)
which states that c
r
lies in the range of U . Recall that we have assumed solutions of
the form
e
ik(x−ct)
= e
ik(x−c
r
t)
e
kc
i
t
,
which means that c
r
is the phase velocity in the positive x direction, and kc
i
is the
growth rate. Equation (12.66) shows that c
r
is positive if U is everywhere positive,

506 Instability
and is negative if U is everywhere negative. In these cases we can say that unstable
waves propagate in the direction of the background flow.
Limits on the maximum growth rate can also be predicted. Equation (12.64) gives
[U
2
+ c
2
r
− 2Uc
r
− c
2
i
]Qdz > 0,
which, on using equation (12.65), becomes
(U
2
− c
2
r
− c
2
i
)Q dz > 0. (12.67)
Now because (U
min
− U) < 0 and (U
max
− U) > 0, it is always true that
(U
min
− U )(U
max
− U)Qdz 0,
which can be recast as
[U
max
U
min
+ U
2
− U(U
max
+ U
min
)]Qdz 0.
Using equation (12.67), this gives
[U
max
U
min
+ c
2
r
+ c
2
i
− U(U
max
+ U
min
)]Qdz 0.
On using equation (12.65), this becomes
[U
max
U
min
+ c
2
r
+ c
2
i
− c
r
(U
max
+ U
min
)]Qdz 0.
Because the quantity within []is independent of z, and
Qdz > 0, we must have
[] 0. With some rearrangement, this condition can be written as
c
r
−
1
2
(U
max
+ U
min
)
2
+ c
2
i
1
2
(U
max
− U
min
)
2
.
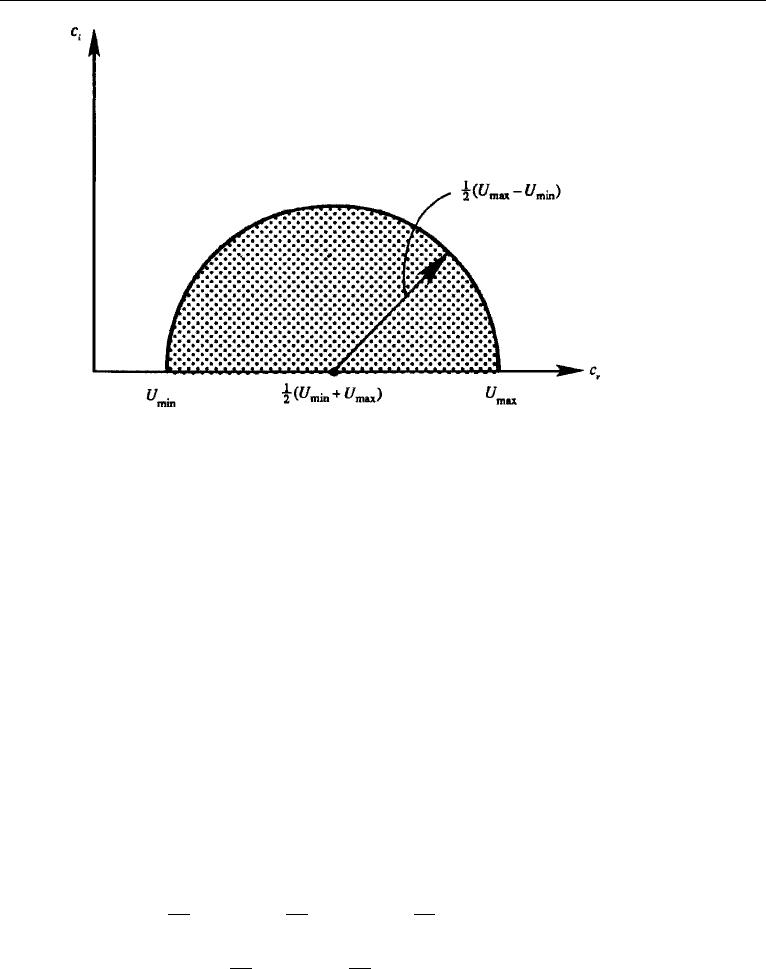
This shows that the complex wave velocity c of any unstable mode of a disturbance
in parallel flows of an inviscid fluid must lie inside the semicircle in the upper half of
the c-plane, which has the range of U as the diameter (Figure 12.20). This is called
the Howard semicircle theorem. It states that the maximum growth rate is limited by
kc
i
<
k
2
(U
max
− U
min
).
The theorem is very useful in searching for eigenvalues c(k) in numerical solution of
instability problems.
8. Squire’s Theorem and Orr–Sommerfeld Equation 507
Figure 12.20 The Howard semicircle theorem. In several inviscid parallel flows the complex eigenvalue
c must lie within the semicircle shown.
8. Squire’s Theorem and Orr–Sommerfeld Equation
In our studies of the B´enard and Taylor problems, we encountered two flows in which
viscosity has a stabilizing effect. Curiously, viscous effects can also be destabilizing,
as indicated by several calculations of wall-bounded parallel flows. In this section we
shall derive the equation governing the stability of parallel flows of a homogeneous
viscous fluid. Let the primary flow be directed along the x direction and vary in the
y direction so that U =[U(y),0, 0]. We decompose the total flow as the sum of the
basic flow plus the perturbation:
˜
u =[U + u, v, w],
˜p = P + p.
Both the background and the perturbed flows satisfy the Navier–Stokes equations.
The perturbed flow satisfies the x-momentum equation
∂u
∂t
+ (U + u)
∂
∂x
(U + u) + v
∂
∂y
(U + u)
=−
∂
∂x
(P + p) +
1
Re
∇
2
(U + u), (12.68)
where the variables have been nondimensionalized by a characteristic length scale L
(say, the width of flow), and a characteristic velocity U
0
(say, the maximum velocity
of the basic flow); time is scaled by L/U
0
and the pressure is scaled by ρU
2
0
. The
Reynolds number is defined as Re = U
0
L/ν.

508 Instability
The background flow satisfies
0 =−
∂P
∂x
+
1
Re
∇
2
U.
Subtracting from equation (12.68) and neglecting terms nonlinear in the perturbations,
we obtain the x-momentum equation for the perturbations:
∂u
∂t
+ U
∂u
∂x
+ v
∂U
∂y
=−
∂p
∂x
+
1
Re
∇
2
u. (12.69)
Similarly the y-momentum, z-momentum, and continuity equations for the
perturbations are
∂v
∂t
+ U
∂v
∂x
=−
∂p
∂y
+
1
Re
∇
2
v,
∂w
∂t
+ U
∂w
∂x
=−
∂p
∂z
+
1
Re
∇
2
w,
∂u
∂x
+
∂v
∂y
+
∂w
∂z
= 0.
(12.70)
The coefficients in the perturbation equations (12.69) and (12.70) depend only on y,
so that the equations admit solutions exponential in x, z, and t. Accordingly, we
assume normal modes of the form
[u,p]=[
ˆ
u(y), ˆp(y)]e
i(kx+mz−kct)
. (12.71)
As the flow is unbounded in x and z, the wavenumber components k and m must be
real. The wave speed c = c
r
+ ic
i
may be complex. Without loss of generality, we
can consider only positive values for k and m; the sense of propagation is then left
open by keeping the sign of c
r
unspecified. The normal modes represent waves that
travel obliquely to the basic flow with a wavenumber of magnitude
√
k
2
+ m
2
and
have an amplitude that varies in time as exp(kc
i
t). Solutions are therefore stable if
c
i
< 0 and unstable if c
i
> 0.
On substitution of the normal modes, the perturbation equations (12.69) and
(12.70) become
ik(U − c) ˆu +ˆvU
y
=−ik ˆp +
1
Re
[ˆu
yy
− (k
2
+ m
2
) ˆu],
ik(U − c) ˆv =−ˆp
y
+
1
Re
[ˆv
yy
− (k
2
+ m
2
) ˆv],
ik(U − c) ˆw =−im ˆp +
1
Re
[ˆw
yy
− (k
2
+ m
2
) ˆw],
ik ˆu +ˆv
y
+ im ˆw = 0,
(12.72)
where subscripts denote derivatives with respect to y. These are the normal mode
equations for three-dimensional disturbances. Before proceeding further, we shall
first show that only two-dimensional disturbances need to be considered.
8. Squire’s Theorem and Orr–Sommerfeld Equation 509
Squire’s Theorem
A very useful simplification of the normal mode equations was achieved by Squire in
1933, showing that to each unstable three-dimensional disturbance there corresponds
a more unstable two-dimensional one. To prove this theorem, consider the Squire
transformation
¯
k = (k
2
+ m
2
)
1/2
, ¯c = c,
¯
k ¯u = k ˆu + m ˆw, ¯v =ˆv,
¯p
¯
k
=
ˆp
k
,
¯
k
Re = k Re.
(12.73)
In substituting these transformations into equation (12.72), the first and third of equa-
tion (12.72) are added; the rest are simply transformed. The result is
i
¯
k(U − c)¯u +¯vU
y
=−i
¯
k ¯p +
1
Re
[¯u
yy
−
¯
k
2
¯u],
i
¯
k(U − c)¯v =−¯p
y
+
1
Re
[¯v
yy
−
¯
k
2
¯v],
i
¯
k ¯u +¯v
y
= 0.
These equations are exactly the same as equation (12.72), but with m =ˆw = 0. Thus,
to each three-dimensional problem corresponds an equivalent two-dimensional one.
Moreover, Squire’s transformation (12.73) shows that the equivalent two-dimensional
problem is associated with a lower Reynolds number as
¯
k>k. It follows that the
critical Reynolds number at which the instability starts is lower for two-dimensional
disturbances. Therefore, we only need to consider a two-dimensional disturbance if
we want to determine the minimum Reynolds number for the onset of instability.
The three-dimensional disturbance (12.71) is a wave propagating obliquely to the
basic flow. If we orient the coordinate system with the new x-axis in this direction, the
equations of motion are such that only the component of basic flow in this direction
affects the disturbance. Thus, the effective Reynolds number is reduced.
An argument without using the Reynolds number is now given because Squire’s
theorem also holds for several other problems that do not involve the Reynolds number.
Equation (12.73) shows that the growth rate for a two-dimensional disturbance is
exp(
¯
k ¯c
i
t), whereas equation (12.71) shows that the growth rate of a three-dimensional
disturbance is exp(kc
i
t). The two-dimensional growth rate is therefore larger because
Squire’s transformation requires
¯
k>kand ¯c = c. We can therefore say that the
two-dimensional disturbances are more unstable.
Orr–Sommerfeld Equation
Because of Squire’s theorem, we only need to consider the set (12.72) with
m =ˆw = 0. The two-dimensionality allows the definition of a streamfunction
ψ(x, y, t) for the perturbation field by
u =
∂ψ
∂y
,v=−
∂ψ
∂x
.

510 Instability
We assume normal modes of the form
[u, v, ψ]=[ˆu, ˆv, φ] e
ik(x−ct)
.
(To be consistent, we should denote the complex amplitude of ψ by
ˆ
ψ; we are using
φ instead to follow the standard notation for this variable in the literature.) Then we
must have
ˆu = φ
y
, ˆv =−ikφ.
A single equation in terms of φ can now be found by eliminating the pressure
from the set (12.72). This gives
(U − c)(φ
yy
− k
2
φ) − U
yy
φ =
1
ik Re
[φ
yyyy
− 2k
2
φ
yy
+ k
4
φ], (12.74)
where subscripts denote derivatives with respect to y. It is a fourth-order ordinary
differential equation. The boundary conditions at the walls are the no-slip conditions
u = v = 0, which require
φ = φ
y
= 0aty = y
1
and y
2
. (12.75)
Equation (12.74) is the well-known Orr–Sommerfeld equation, which governs
the stability of nearly parallel viscous flows such as those in a straight channel or in
a boundary layer. It is essentially a vorticity equation because the pressure has been
eliminated. Solutions of the Orr–Sommerfeld equations are difficult to obtain, and
only the results of some simple flows will be discussed in the later sections. However,
we shall first discuss certain results obtained by ignoring the viscous term in this
equation.
9. Inviscid Stability of Parallel Flows
Useful insights into the viscous stability of parallel flows can be obtained by first
assuming that the disturbances obey inviscid dynamics. The governing equation can
be found by letting Re →∞in the Orr–Sommerfeld equation, giving
(U − c)[φ
yy
− k
2
φ]−U
yy
φ = 0, (12.76)
which is called the Rayleigh equation. If the flow is bounded by walls at y
1
and y
2
where v = 0, then the boundary conditions are
φ = 0aty = y
1
and y
2
. (12.77)
The set (12.76) and (12.77) defines an eigenvalue problem, with c(k) as the eigenvalue
and φ as the eigenfunction. As the equations do not involve i, taking the complex
conjugate shows that if φ is an eigenfunction with eigenvalue c for some k, then
φ
∗
is also an eigenfunction with eigenvalue c
∗
for the same k. Therefore, to each
eigenvalue with a positive c
i
there is a corresponding eigenvalue with a negative c
i
.

9. Inviscid Stability of Parallel Flows 511
In other words, to each growing mode there is a corresponding decaying mode. Stable
solutions therefore can have only a real c. Note that this is true of inviscid flows only.
The viscous term in the full Orr–Sommerfeld equation (12.74) involves an i, and the
foregoing conclusion is no longer valid.
We shall now show that certain velocity distributions U(y)are potentially unsta-
ble according to the inviscid Rayleigh equation (12.76). In this discussion it should
be noted that we are only assuming that the disturbances obey inviscid dynamics; the
background flow U(y) may be chosen to be chosen to be any profile, for example,
that of viscous flows such as Poiseuille flow or Blasius flow.
Rayleigh’s Inflection Point Criterion
Rayleigh proved that a necessary (but not sufficient) criterion for instability of an
inviscid parallel flow is that the basic velocity profile U(y) has a point of inflection.
To prove the theorem, rewrite the Rayleigh equation (12.76) in the form
φ
yy
− k
2
φ −
U
yy
U − c
φ = 0,
and consider the unstable mode for which c
i
> 0, and therefore U −c = 0. Multiply
this equation by φ
∗
, integrate from y
1
to y
2
, by parts if necessary, and apply the
boundary condition φ = 0 at the boundaries. The first term transforms as follows:
φ
∗
φ
yy
dy =[φ
∗
φ
y
]
y
2
y
1
−
φ
∗
y
φ
y
dy =−
|φ
y
|
2
dy,
where the limits on the integrals have not been explicitly written. The Rayleigh
equation then gives
[|φ
y
|
2
+ k
2
|φ|
2
]dy +
U
yy
U − c
|φ|
2
dy = 0. (12.78)
The first term is real. The imaginary part of the second term can be found by multi-
plying the numerator and denominator by (U − c
∗
). The imaginary part of equation
(12.78) then gives
c
i
U
yy
|φ|
2
|U − c|
2
dy = 0. (12.79)
For the unstable case, for which c
i
= 0, equation (12.79) can be satisfied only if
U
yy
changes sign at least once in the open interval y
1
<y<y
2
. In other words, for
instability the background velocity distribution must have at least one point of inflec-
tion (where U
yy
= 0) within the flow. Clearly, the existence of a point of inflection
does not guarantee a nonzero c
i
. The inflection point is therefore a necessary but not
sufficient condition for inviscid instability.
Fjortoft’s Theorem
Some seventy years after Rayleigh’s discovery, the Swedish meteorologist Fjortoft in
1950 discovered a stronger necessary condition for the instability of inviscid parallel
