Cohen I.M., Kundu P.K. Fluid Mechanics
Подождите немного. Документ загружается.

472 Instability
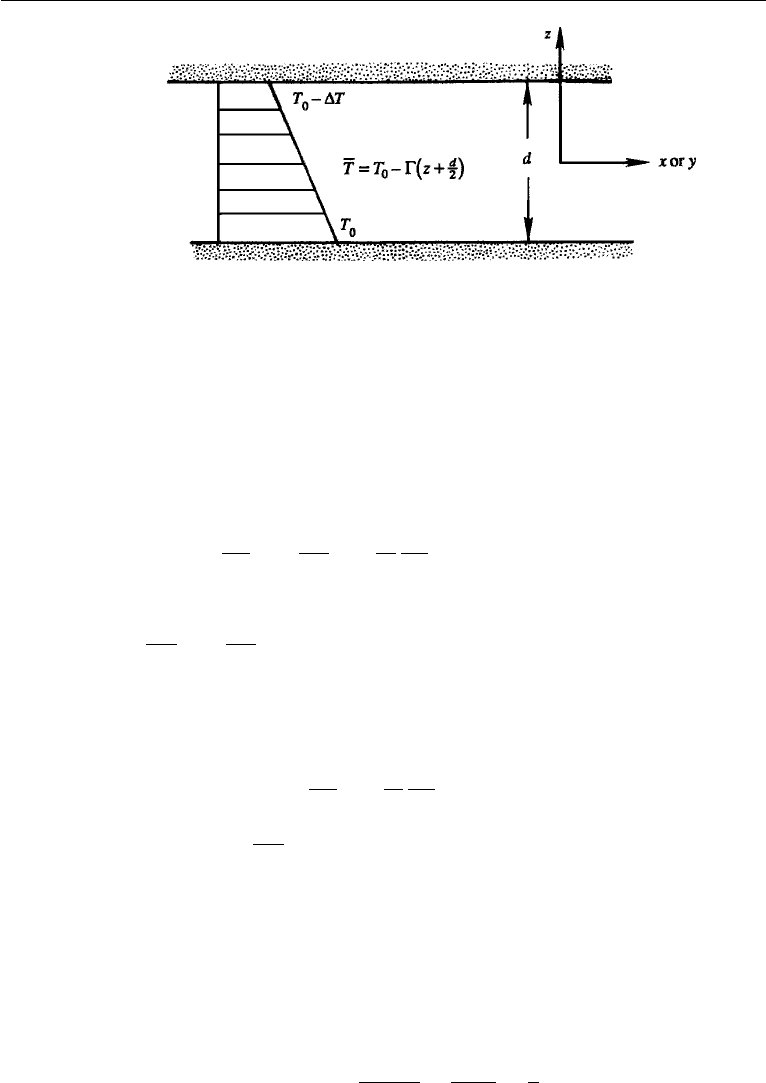
Figure 12.2 Definition sketch for the B´enard problem.
The preceding heat equation gives the linear vertical temperature distribution
¯
T = T
0
− (z + d/2), (12.6)
where ≡ T /d is the magnitude of the vertical temperature gradient, and T
0
is
the temperature of the lower wall (Figure 12.2). Substituting equation (12.4) into
equation (12.3), we obtain
∂u
i
∂t
+ u
j
∂u
i
∂x
j
=−
1
ρ
0
∂
∂x
i
(P + p)
− g[1 − α(
¯
T + T
− T
0
)]δ
i3
+ ν∇
2
u
i
,
∂T
∂t
+ u
j
∂
∂x
j
(
¯
T + T
) = κ∇
2
(
¯
T + T
).
(12.7)
Subtracting the mean state equation (12.5) from the perturbed state equation (12.7),
and neglecting squares of perturbations, we have
∂u
i
∂t
=−
1
ρ
0
∂p
∂x
i
+ gαT
δ
i3
+ ν∇
2
u
i
, (12.8)
∂T
∂t
− w = κ∇
2
T
, (12.9)
where w is the vertical component of velocity. The advection term in equation (12.9)
results from u
j
(∂
¯
T/∂x
j
) = w(d
¯
T/dz)=−w. Equations (12.8) and (12.9) govern
the behavior of perturbations on the system.
At this point it is useful to pause and show that the Rayleigh number defined by
equation (12.2) is the ratio of buoyancy force to viscous force. From equation (12.9),
the velocity scale is found by equating the advective and diffusion terms, giving
w ∼
κT
/d
2
∼
κ/d
=
κ
d
.
3. Thermal Instability: The B´enard Problem 473
An examination of the last two terms in equation (12.8) shows that
Buoyancy force
Viscous force
∼
gαT
νw/d
2
∼
gαd
νw/d
2
=
gαd
4
νκ
,
which is the Rayleigh number.
We now write the perturbation equations in terms of w and T
only. Taking the
Laplacian of the i = 3 component of equation (12.8), we obtain
∂
∂t
(∇
2
w) =−
1
ρ
0
∇
2
∂p
∂z
+ gα∇
2
T
+ ν∇
4
w. (12.10)
The pressure term in equation (12.10) can be eliminated by taking the divergence of
equation (12.8) and using the continuity equation ∂u
i
/∂x
i
= 0. This gives
0 =−
1
ρ
0
∂
2
p
∂x
i
∂x
i
+ gα
∂T
∂x
i
δ
i3
+ 0.
Differentiating with respect to z, we obtain
0 =−
1
ρ
0
∇
2
∂p
∂z
+ gα
∂
2
T
∂z
2
,
so that equation (12.10) becomes
∂
∂t
(∇
2
w) = gα∇
2
H
T
+ ν∇
4
w, (12.11)
where ∇
2
H
≡ ∂
2
/∂x
2
+ ∂
2
/∂y
2
is the horizontal Laplacian operator.
Equations (12.9) and (12.11) govern the development of perturbations on the
system. The boundary conditions on the upper and lower rigid surfaces are that the
no-slip condition is satisfied and that the walls are maintained at constant tempera-
tures. These conditions require u = v = w = T
= 0atz =±d/2. Because the
conditions on u and v hold for all x and y, it follows from the continuity equation
that ∂w/∂z = 0 at the walls. The boundary conditions therefore can be written as
w =
∂w
∂z
= T
= 0atz =±
d
2
. (12.12)
We shall use dimensionless independent variables in the rest of the analysis. For
this, we make the transformation
t →
d
2
κ
t,
(x,y,z) → (xd,yd,zd),
where the old variables are on the left-hand side and the new variables are on the
right-hand side; note that we are avoiding the introduction of new symbols for the

474 Instability
nondimensional variables. Equations (12.9), (12.11), and (12.12) then become
∂
∂t
−∇
2
T
=
d
2
κ
w, (12.13)
1
Pr
∂
∂t
−∇
2
∇
2
w =
gαd
2
ν
∇
2
H
T
, (12.14)
w =
∂w
∂z
= T
= 0atz =±
1
2
(12.15)
where Pr ≡ ν/κ is the Prandtl number.
The method of normal modes is now introduced. Because the coefficients of the
governing set (12.13) and (12.14) are independent of x, y, and t, solutions exponential
in these variables are allowed. We therefore assume normal modes of the form
w =ˆw(z) e
ikx+ily+σt
,
T
=
ˆ
T(z)e
ikx+ily+σt
.
The requirement that solutions remain bounded as x, y →∞ implies that the
wavenumbers k and l must be real. In other words, the normal modes must be peri-
odic in the directions of unboundedness. The growth rate σ = σ
r
+ iσ
i
is allowed
to be complex. With this dependence, the operators in equations (12.13) and (12.14)
transform as follows:
∂
∂t
→ σ,
∇
2
H
→−K
2
,
∇
2
→
d
2
dz
2
− K
2
,
where K =
√
k
2
+ l
2
is the magnitude of the (nondimensional) horizontal wave-
number. Equations (12.13) and (12.14) then become
[σ − (D
2
− K
2
)]
ˆ
T =
d
2
κ
ˆw, (12.16)
σ
Pr
− (D
2
− K
2
)
(D
2
− K
2
) ˆw =−
gαd
2
K
2
ν
ˆ
T, (12.17)
where D ≡ d/dz. Making the substitution
d
2
κ
ˆw ≡ W.
Equations (12.16) and (12.17) become
[σ − (D
2
− K
2
)]
ˆ
T = W, (12.18)
σ
Pr
− (D
2
− K
2
)
(D
2
− K
2
)W =−Ra K
2
ˆ
T, (12.19)

3. Thermal Instability: The B´enard Problem 475
where
Ra ≡
gαd
4
κν
,
is the Rayleigh number. The boundary conditions (12.15) become
W = DW =
ˆ
T = 0atz =±
1
2
. (12.20)
Before we can proceed further, we need to show that σ in this problem can only
be real.
Proof That σ Is Real for Ra > 0
The sign of the real part of σ(= σ
r
+ iσ
i
) determines whether the flow is stable or
unstable. We shall now show that for the B´enard problem σ is real, and the marginal
state that separates stability from instability is governed by σ = 0. To show this,
multiply equation (12.18) by
ˆ
T
∗
(the complex conjugate of
ˆ
T ), and integrate between
±
1
2
, by parts if necessary, using the boundary conditions (12.20). The various terms
transform as follows:
σ
ˆ
T
∗
ˆ
Tdz= σ
|
ˆ
T |
2
dz,
ˆ
T
∗
D
2
ˆ
Tdz=[
ˆ
T
∗
D
ˆ
T ]
1/2
−1/2
−
D
ˆ
T
∗
D
ˆ
Tdz=−
|D
ˆ
T |
2
dz,
where the limits on the integrals have not been explicitly written. Equation (12.18)
then becomes
σ
|
ˆ
T |
2
dz +
|D
ˆ
T |
2
dz + K
2
|
ˆ
T |
2
dz =
ˆ
T
∗
Wdz,
which can be written as
σI
1
+ I
2
=
ˆ
T
∗
Wdz, (12.21)
where
I
1
≡
|
ˆ
T |
2
dz,
I
2
≡
[|D
ˆ
T |
2
+ K
2
|
ˆ
T |
2
]dz.

476 Instability
Similarly, multiply equation (12.19) by W
∗
and integrate by parts. The first term in
equation (12.19) gives
σ
Pr
W
∗
(D
2
− K
2
)W dz =
σ
Pr
W
∗
D
2
Wdz−
σK
2
Pr
W
∗
Wdz
=−
σ
Pr
[|DW|
2
+ K
2
|W |
2
]dz. (12.22)
The second term in (12.19) gives
W
∗
(D
2
− K
2
)(D
2
− K
2
)W dz
=
W
∗
(D
4
+ K
4
− 2K
2
D
2
)W dz
=
W
∗
D
4
Wdz+ K
4
W
∗
Wdz− 2K
2
W
∗
D
2
Wdz
=[W
∗
D
3
W ]
1/2
−1/2
−
DW
∗
D
3
Wdz+ K
4
|W |
2
dz
− 2K
2
[W
∗
DW]
1/2
−1/2
+ 2K
2
DW
∗
DW dz
=
[|D
2
W |
2
+ 2K
2
|DW|
2
+ K
4
|W |
2
]dz. (12.23)
Using equations (12.22) and (12.23), the integral of equation (12.19) becomes
σ
Pr
J
1
+ J
2
= Ra K
2
W
∗
ˆ
Tdz, (12.24)
where
J
1
≡
[|DW|
2
+ K
2
|W |
2
]dz,
J
2
≡
[|D
2
W |
2
+ 2K
2
|DW|
2
+ K
4
|W |
2
]dz.
Note that the four integrals I
1
, I
2
, J
1
, and J
2
are all positive. Also, the right-hand
side of equation (12.24) is Ra K
2
times the complex conjugate of the right-hand side
of equation (12.21). We can therefore eliminate the integral on the right-hand side of
these equations by taking the complex conjugate of equation (12.21) and substituting
into equation (12.24). This gives
σ
Pr
J
1
+ J
2
= Ra K
2
(σ
∗
I
1
+ I
2
).
Equating imaginary parts
σ
i
J
1
Pr
+ Ra K
2
I
1
= 0.

3. Thermal Instability: The B´enard Problem 477
We consider only the top-heavy case, for which Ra > 0. The quantity within []is
then positive, and the preceding equation requires that σ
i
= 0.
The B´enard problem is one of two well-known problems in which σ is real.
(The other one is the Taylor problem of Couette flow between rotating cylinders,
discussed in the following section.) In most other problems σ is complex, and the
marginal state (σ
r
= 0) contains propagating waves. In the B´enard and Taylor prob-
lems, however, the marginal state corresponds to σ = 0, and is therefore stationary
and does not contain propagating waves. In these the onset of instability is marked
by a transition from the background state to another steady state. In such a case we
commonly say that the principle of exchange of stabilities is valid, and the instability
sets in as a cellular convection, which will be explained shortly.
Solution of the Eigenvalue Problem with Two Rigid Plates
First, we give the solution for the case that is easiest to realize in a laboratory exper-
iment, namely, a layer of fluid confined between two rigid plates where no-slip con-
ditions are satisfied. The solution to this problem was first given by Jeffreys in 1928.
A much simpler solution exists for a layer of fluid with two stress-free surfaces. This
will be discussed later.
For the marginal state σ = 0, and the set (12.18) and (12.19) becomes
(D
2
− K
2
)
ˆ
T =−W,
(D
2
− K
2
)
2
W = Ra K
2
ˆ
T.
(12.25)
Eliminating
ˆ
T , we obtain
(D
2
− K
2
)
3
W =−Ra K
2
W. (12.26)
The boundary condition (12.20) becomes
W = DW = (D
2
− K
2
)
2
W = 0atz =±
1
2
. (12.27)
We have a sixth-order homogeneous differential equation with six homogeneous
boundary conditions. Nonzero solutions for such a system can only exist for a partic-
ular value of Ra (for a given K). It is therefore an eigenvalue problem. Note that the
Prandtl number has dropped out of the marginal state.
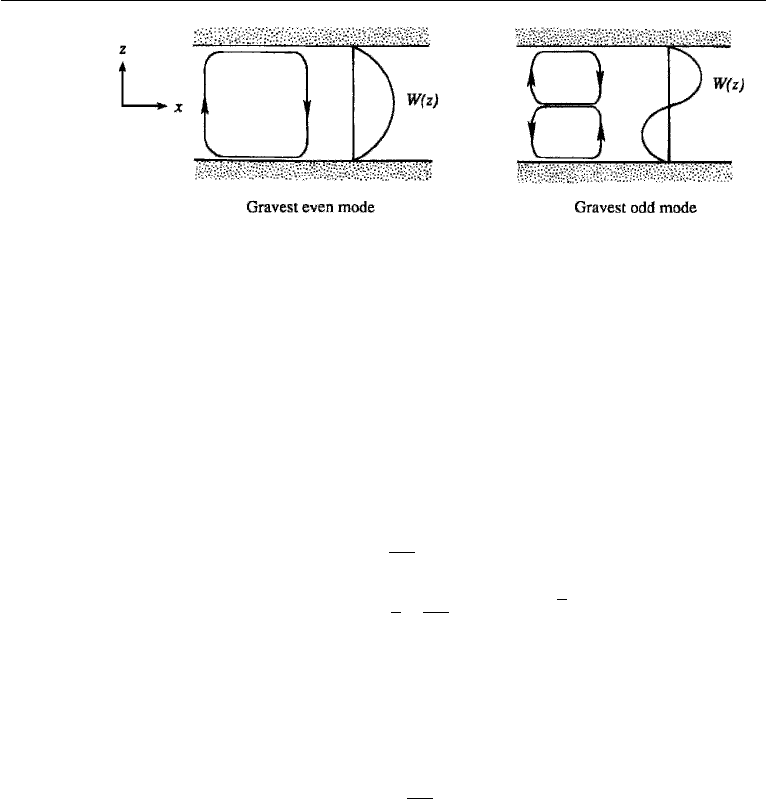
The point to observe is that the problem is symmetric with respect to the two
boundaries, thus the eigenfunctions fall into two distinct classes—those with the
vertical velocity symmetric about the midplane z = 0, and those with the vertical
velocity antisymmetric about the midplane (Figure 12.3). The gravest even mode
therefore has one row of cells, and the gravest odd mode has two rows of cells. It can be
shown that the smallest critical Rayleigh number is obtained by assuming disturbances
in the form of the gravest even mode, which also agrees with experimental findings
of a single row of cells.
478 Instability
Figure 12.3 Flow pattern and eigenfunction structure of the gravest even mode and the gravest odd mode
in the B´enard problem.
Because the coefficients of the governing equations (12.26) are independent of z,
the general solution can be expressed as a superposition of solutions of the form
W = e
qz
,
where the six roots of q are given by
(q
2
− K
2
)
3
=−Ra K
2
.
The three roots of this equation are
q
2
=−K
2
Ra
K
4
1/3
− 1
,
q
2
= K
2
1 +
1
2
Ra
K
4
1/3
(1 ± i
√
3)
.
(12.28)
Taking square roots, the six roots finally become
±iq
0
, ±q, and ± q
∗
,
where
q
0
= K
Ra
K
4
1/3
− 1
1/2
,
and q and its conjugate q
∗
are given by the two roots of equation (12.28).
The even solution of equation (12.26) is therefore
W = A cos q
0
z + B cosh qz + C cosh q
∗
z.
To apply the boundary conditions on this solution, we find the following
derivatives:
DW =−Aq
0
sin q
0
z + Bq sinh qz +Cq
∗
sinh q
∗
z,
(D
2
− K
2
)
2
W = A(q
2
0
+ K
2
)
2
cos q
0
z + B(q
2
− K
2
)
2
cosh qz
+ C(q
∗2
− K
2
)
2
cosh q
∗
z.
3. Thermal Instability: The B´enard Problem 479
The boundary conditions (12.27) then require
cos
q
0
2
cosh
q
2
cosh
q
∗
2
−q
0
sin
q
0
2
q sinh
q
2
q
∗
sinh
q
∗
2
(q
2
0
+ K
2
)
2
cos
q
0
2
(q
2
− K
2
)
2
cosh
q
2
(q
∗2
− K
2
)
2
cosh
q
∗
2
A
B
C
= 0.
Here, A, B, and C cannot all be zero if we want to have a nonzero solution, which
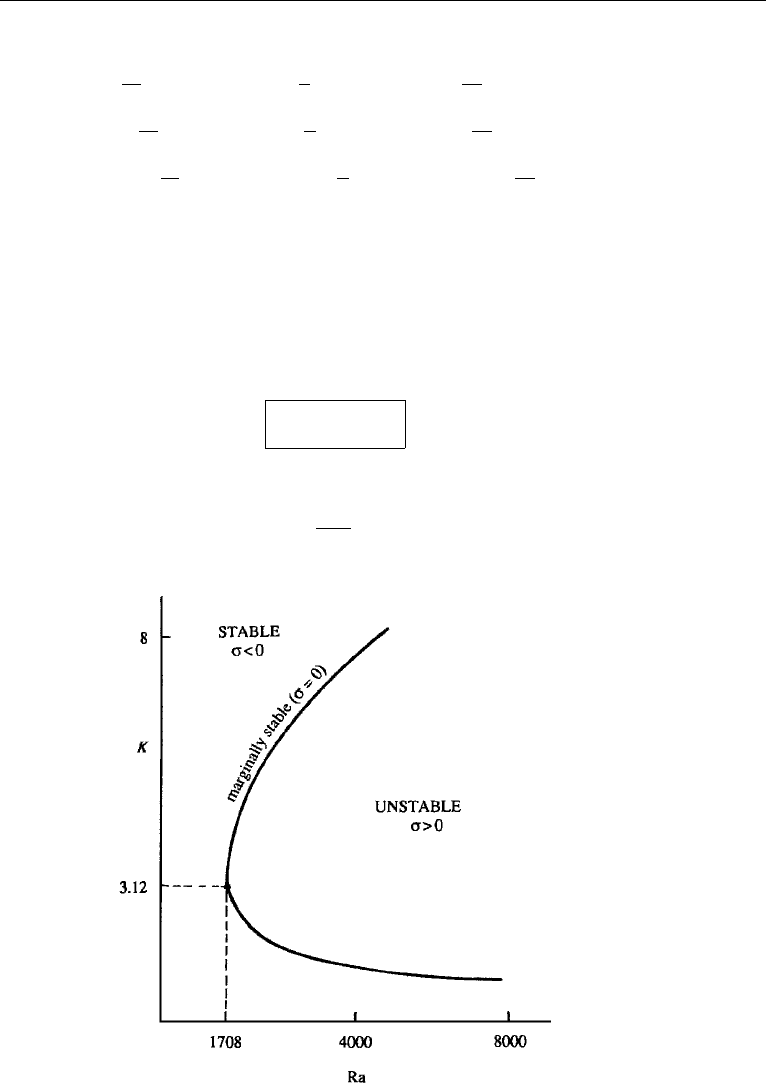
requires that the determinant of the matrix must vanish. This gives a relation between
Ra and the corresponding eigenvalue K (Figure 12.4). Points on the curve K(Ra)
represent marginally stable states, which separate regions of stability and instability.
The lowest value of Ra is found to be Ra
cr
= 1708, attained at K
cr
= 3.12. As all
values of K are allowed by the system, the flow first becomes unstable when the
Rayleigh number reaches a value of
Ra
cr
= 1708.
The wavelength at the onset of instability is
λ
cr
=
2πd
K
cr
2d.
Figure 12.4 Stable and unstable regions for B´enard convection.

480 Instability
Laboratory experiments agree remarkably well with these predictions, and the
solution of the B´enard problem is considered one of the major successes of the linear
stability theory.
Solution with Stress-Free Surfaces
We now give the solution for a layer of fluid with stress-free surfaces. This case can
be approximately realized in a laboratory experiment if a layer of liquid is floating on
top of a somewhat heavier liquid. The main interest in the problem, however, is that it
allows a simple solution, which was first given by Rayleigh. In this case the boundary
conditions are w = T
= µ(∂u/∂z + ∂w/∂x) = µ(∂v/∂z + ∂w/∂y) = 0 at the
surfaces, the latter two conditions resulting from zero stress. Because w vanishes (for
all x and y) on the boundaries, it follows that the vanishing stress conditions require
∂u/∂z = ∂v/∂z = 0 at the boundaries. On differentiating the continuity equation
with respect to z, it follows that ∂
2
w/∂z
2
= 0 on the free surfaces. In terms of the
complex amplitudes, the eigenvalue problem is therefore
(D
2
− K
2
)
3
W =−Ra K
2
W, (12.29)
with W = (D
2
− K
2
)
2
W = D
2
W = 0 at the surfaces. By expanding (D
2
− K
2
)
2
,
the boundary conditions can be written as
W = D
2
W = D
4
W = 0atz =±
1
2
,
which should be compared with the conditions (12.27) for rigid boundaries.
Successive differentiation of equation (12.29) shows that all even derivatives of
W vanish on the boundaries. The eigenfunctions must therefore be
W = A sin nπz,
where A is any constant and n is an integer. Substitution into equation (12.29) leads
to the eigenvalue relation
Ra = (n
2
π
2
+ K
2
)
3
/K
2
, (12.30)
which gives the Rayleigh number in the marginal state. For a given K
2
, the lowest
value of Ra occurs when n = 1, which is the gravest mode. The critical Rayleigh
number is obtained by finding the minimum value of Ra as K
2
is varied, that is, by
setting d Ra/dK
2
= 0. This gives
d Ra
dK
2
=
3(π
2
+ K
2
)
2
K
2
−
(π
2
+ K
2
)
3
K
4
= 0,
which requires K
2
cr
= π
2
/2. The corresponding value of Ra is
Ra
cr
=
27
4
π
4
= 657.
For a layer with a free upper surface (where the stress is zero) and a rigid bottom
wall, the solution of the eigenvalue problem gives Ra
cr
= 1101 and K
cr
= 2.68.

3. Thermal Instability: The B´enard Problem 481
This case is of interest in laboratory experiments having the most visual effects, as
originally conducted by B´enard.
Cell Patterns
The linear theory specifies the horizontal wavelength at the onset of instability, but
not the horizontal pattern of the convective cells. This is because a given wavenumber
vector K can be decomposed into two orthogonal components in an infinite number of
ways. If we assume that the experimental conditions are horizontally isotropic, with
no preferred directions, then regular polygons in the form of equilateral triangles,
squares, and regular hexagons are all possible structures. B´enard’s original experi-
ments showed only hexagonal patterns, but we now know that he was observing a
different phenomenon. The observations summarized in Drazin and Reid (1981) indi-
cate that hexagons frequently predominate initially. As Ra is increased, the cells tend
to merge and form rolls, on the walls of which the fluid rises or sinks (Figure 12.5).
The cell structure becomes more chaotic as Ra is increased further, and the flow
becomes turbulent when Ra > 5 × 10
4
.
The magnitude or direction of flow in the cells cannot be predicted by linear
theory. After a short time of exponential growth, the flow becomes large enough for
the nonlinear terms to be important and reaches a nonlinear equilibrium stage. The
flow pattern for a hexagonal cell is sketched in Figure 12.6. Particles in the middle
of the cell usually rise in a liquid and fall in a gas. This has been attributed to the
Figure 12.5 Convection rolls in a B´enard problem.
Figure 12.6 Flow pattern in a hexagonal B´enard cell.
