Cohen I.M., Kundu P.K. Fluid Mechanics
Подождите немного. Документ загружается.


452 Computational Fluid Dynamics
equations,
∂u
∂t
+ u
∂u
∂x
+ v
∂u
∂y
˜ud −
p
∂ ˜u
∂x
d
+
1
Re
2
∂u
∂x
∂ ˜u
∂x
+
∂u
∂y
+
∂v
∂x
∂ ˜u
∂y
d = 0, (11.157)
∂v
∂t
+ u
∂v
∂x
+ v
∂v
∂y
˜vd −
p
∂ ˜v
∂y
d
+
1
Re
∂u
∂y
+
∂v
∂x
∂ ˜v
∂x
+2
∂v
∂y
∂ ˜v
∂y
d = 0. (11.158)
The weak form of the continuity equation (11.135) is expressed as
−
∂u
∂x
+
∂v
∂y
˜pd= 0. (11.159)
Given a triangulation of the computational domain, for example, the mesh shown
in Figure 11.16, the weak formulation of (11.157) to (11.159) can be approximated by
the Galerkin finite element formulation based on the finite-dimensional discretization
of the flow variables. The Galerkin formulation can be written as,
h
∂u
h
∂t
+ u
h
∂u
h
∂x
+ v
h
∂u
h
∂y
˜u
h
d −
h
p
h
∂ ˜u
h
∂x
d
+
1
Re
h
2
∂u
h
∂x
∂ ˜u
h
∂x
+
∂u
h
∂y
+
∂v
h
∂x
∂ ˜u
h
∂y
d =0, (11.160)
h
∂v
h
∂t
+ u
h
∂v
h
∂x
+ v
h
∂v
h
∂y
˜v
h
d −
h
p
h
∂ ˜v
h
∂y
d
+
1
Re
h
∂u
h
∂y
+
∂v
h
∂x
∂ ˜v
h
∂x
+ 2
∂v
h
∂y
∂ ˜v
h
∂y
d =0, (11.161)
and −
h
∂u
h
∂x
+
∂v
h
∂y
˜p
h
d = 0, (11.162)
where h indicates a given triangulation of the computational domain.
The time derivatives in (11.160) and (11.161) can be discretized by finite differ-
ence methods. We first evaluate all the terms in (11.160) to (11.162) at a given time
instant t = t
n+1
(fully implicit discretization). Then the time derivative in (11.160)
and (11.161) can be approximated as
∂u
∂t
(
x,t
n+1
)
≈ α
u
(
x,t
n+1
)
− u
(
x,t
n
)
t
− β
∂u
∂t
(
x,t
n
)
, (11.163)

5. Three Examples 453
where t = t
n+1
− t
n
is the time step. The approximation in (11.163) is first-order
accurate in time when α = 1 and β = 0. It can be improved to second-order accurate
by selecting α = 2 and β = 1 which is a variation of the well-known Crank-Nicolson
scheme.
As (11.160) and (11.161) are nonlinear, iterative methods are often used for the
solution. In Newton’s method, the flow variables at the current time t = t
n+1
are
often expressed as
u
h
(
x,t
n+1
)
= u
∗
(
x,t
n+1
)
+ u
(
x,t
n+1
)
,
p
h
(
x,t
n+1
)
= p
∗
(
x,t
n+1
)
+ p
(
x,t
n+1
)
, (11.164)
where u
∗
and p
∗
are the guesstimated values of velocity and pressure during the
iteration. u
and p
are the corrections sought at each iteration.
Substituting (11.163) and (11.164) into Galerkin formulation (11.160) to (11.162),
and linearizing the equations with respect to the correction variables, we have
h
α
t
u
+ u
∗
∂u
∂x
+ v
∗
∂u
∂y
+
∂u
∗
∂x
u
+
∂u
∗
∂y
v
˜u
h
d −
h
p
∂ ˜u
h
∂x
d
+
1
Re
h
2
∂u
∂x
∂ ˜u
h
∂x
+
∂u
∂y
+
∂v
∂x
∂ ˜u
h
∂y
d
=−
h
α
t
u
∗
− u
(
t
n
)
− β
∂u
∂t
(
t
n
)
+ u
∗
∂u
∗
∂x
+ v
∗
∂u
∗
∂y
˜u
h
d
+
h
p
∗
∂ ˜u
h
∂x
d −
1
Re
h
2
∂u
∗
∂x
∂ ˜u
h
∂x
+
∂u
∗
∂y
+
∂v
∗
∂x
∂ ˜u
h
∂y
d,
(11.165)
h
α
t
v
+ u
∗
∂v
∂x
+ v
∗
∂v
∂y
+
∂v
∗
∂x
u
+
∂v
∗
∂y
v
˜v
h
d −
h
p
∂ ˜v
h
∂y
d
+
1
Re
h
∂u
∂y
+
∂v
∂x
∂ ˜v
h
∂x
+ 2
∂v
∂y
∂ ˜v
h
∂y
d
=−
h
α
t
v
∗
− v
(
t
n
)
− β
∂v
∗
∂t
(
t
n
)
+ u
∗
∂v
∗
∂x
+ v
∗
∂v
∗
∂y
˜v
h
d
+
h
p
∗
∂ ˜v
h
∂y
d −
1
Re
h
∂u
∗
∂y
+
∂v
∗
∂x
∂ ˜v
h
∂x
+ 2
∂v
∗
∂y
∂ ˜v
h
∂y
d,
(11.166)
and
−
h
∂u
∂x
+
∂v
∂y
˜p
h
d =
h
∂u
∗
∂x
+
∂v
∗
∂y
˜p
h
d. (11.167)

454 Computational Fluid Dynamics
As the functions in the integrals, unless specified otherwise, are all evaluated at
the current time instant t
n+1
, the temporal discretization in (11.165) and (11.166) is
fully implicit and unconditionally stable. The terms on the right-hand-side of (11.165)
to (11.167) represent the residuals of the corresponding equations and can be used to
monitor the convergence of the nonlinear iteration.
Similar to the one-dimensional case in Section 3, the finite-dimensional dis-
cretization of the flow variables can be constructed using shape (or interpolation)
functions,
u
=
A
u
A
N
u
A
(
x,y
)
,v
=
A
v
A
N
u
A
(
x,y
)
,p
=
B
p
B
N
p
B
(
x,y
)
,
(11.168)
where N
u
A
(
x,y
)
and N
p
B
(
x,y
)
are the shape functions for the velocity and the pres-
sure, respectively. They are not necessarily the same. In order to satisfy the LBB
stability condition, the shape function N
u
A
(
x,y
)
in the mixed finite element formu-
lation should be one order higher than N
p
B
(
x,y
)
, as discussed in Section 4. The
summation over A is through all the velocity nodes, while the summation over B runs
through all the pressure nodes. The variational functions may be expressed in terms
of the same shape functions,
˜u
h
=
A
˜u
A
N
u
A
(
x,y
)
, ˜v
h
=
A
˜v
A
N
u
A
(
x,y
)
, ˜p
h
=
B
˜p
B
N
p
B
(
x,y
)
.
(11.169)
Since the Galerkin formulation (11.165) to (11.167) is valid for all possible
choices of the variational functions, the coefficients in (11.169) should be arbitrary.
In this way, the Galerkin formulation (11.165) to (11.167) reduces to a system of
algebraic equations,
A
u
A
h
α
t
N
u
A
+ u
∗
∂N
u
A
∂x
+ v
∗
∂N
u
A
∂y
+
∂u
∗
∂x
N
u
A
N
u
A
+
1
Re
2
∂N
u
A
∂x
∂N
u
A
∂x
+
∂N
u
A
∂y
∂N
u
A
∂y
d
+
A
v
A
h
∂u
∗
∂y
N
u
A
N
u
A
+
1
Re
∂N
u
A
∂x
∂N
u
A
∂y
d −
B
p
B
h
N
p
B
∂N
u
A
∂x
d
=−
h
α
t
u
∗
− u
(
t
n
)
− β
∂u
∂t
(
t
n
)
+ u
∗
∂u
∗
∂x
+ v
∗
∂u
∗
∂y
N
u
A
d
+
h
p
∗
∂N
u
A
∂x
d −
1
Re
h
2
∂u
∗
∂x
∂N
u
A
∂x
+
∂u
∗
∂y
+
∂v
∗
∂x
∂N
u
A
∂y
d,
(11.170)

5. Three Examples 455
A
v
A
h
α
t
N
u
A
+ u
∗
∂N
u
A
∂x
+ v
∗
∂N
u
A
∂y
+
∂u
∗
∂y
N
u
A
N
u
A
+
1
Re
∂N
u
A
∂x
∂N
u
A
∂x
+ 2
∂N
u
A
∂y
∂N
u
A
∂y
d
+
A
u
A
h
∂v
∗
∂x
N
u
A
N
u
A
+
1
Re
∂N
u
A
∂y
∂N
u
A
∂x
d −
B
p
B
h
N
p
B
∂N
u
A
∂y
d
=−
h
α
t
v
∗
− v
(
t
n
)
− β
∂v
∗
∂t
(
t
n
)
+ u
∗
∂v
∗
∂x
+ v
∗
∂v
∗
∂y
N
u
A
d
+
h
p
∗
∂N
u
A
∂y
d −
1
Re
h
∂u
∗
∂y
+
∂v
∗
∂x
∂N
u
A
∂x
+ 2
∂v
∗
∂y
∂N
u
A
∂y
d,
(11.171)
and
−
A
u
A
h
∂N
u
A
∂x
N
p
B
d −
A
v
A
h
∂N
u
A
∂y
N
p
B
d
=
h
∂u
∗
∂x
+
∂v
∗
∂y
N
p
B
d, (11.172)
for all the velocity nodes A and pressure nodes B. Equations (11.170) to (11.172) can
be organized into a matrix form,
A
uu
A
uv
B
up
A
vu
A
vv
B
vp
B
T
up
B
T
vp
0
u
v
p
=
f
u
f
v
f
p
, (11.173)
where
A
uu
=
A
uu
AA
, A
uv
=
A
uv
AA
, B
up
=
B
up
AB
,
A
vu
=
A
vu
AA
, A
vv
=
A
vv
AA
, B
vp
=
B
vp
AB
, (11.174)
u =
{
u
A
}
, v =
{
v
A
}
, p =
{
p
B
}
,
f
u
=
f
u
A
, f
v
=
f
v
A
, f
p
=
f
p
B
,
and
A
uu
AA
=
h
α
t
N
u
A
+ u
∗
∂N
u
A
∂x
+ v
∗
∂N
u
A
∂y
+
∂u
∗
∂x
N
u
A
N
u
A
+
1
Re
2
∂N
u
A
∂x
∂N
u
A
∂x
+
∂N
u
A
∂y
∂N
u
A
∂y
d, (11.175)
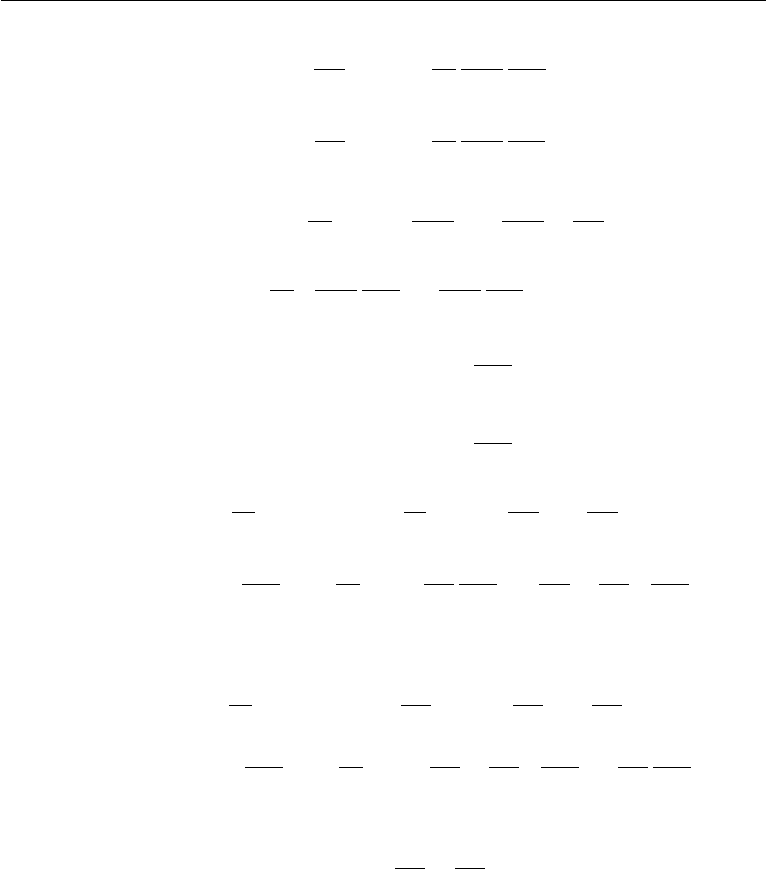
456 Computational Fluid Dynamics
A
uv
AA
=
h
∂u
∗
∂y
N
u
A
N
u
A
+
1
Re
∂N
u
A
∂x
∂N
u
A
∂y
d, (11.176)
A
vu
AA
=
h
∂v
∗
∂x
N
u
A
N
u
A
+
1
Re
∂N
u
A
∂y
∂N
u
A
∂x
d, (11.177)
A
vv
AA
=
h
α
t
N
u
A
+ u
∗
∂N
u
A
∂x
+ v
∗
∂N
u
A
∂y
+
∂v
∗
∂y
N
u
A
N
u
A
+
1
Re
∂N
u
A
∂x
∂N
u
A
∂x
+ 2
∂N
u
A
∂y
∂N
u
A
∂y
d, (11.178)
B
up
AB
=−
h
N
p
B
∂N
u
A
∂x
d, (11.179)
B
vp
AB
=−
h
N
p
B
∂N
u
A
∂y
d, (11.180)
f
u
A
=−
h
α
t
u
∗
− u
(
t
n
)
− β
∂u
∂t
(
t
n
)
+ u
∗
∂u
∗
∂x
+ v
∗
∂u
∗
∂y
N
u
A
d
+
h
p
∗
∂N
u
A
∂x
d −
1
Re
h
2
∂u
∗
∂x
∂N
u
A
∂x
+
∂u
∗
∂y
+
∂v
∗
∂x
∂N
u
A
∂y
d ,
(11.181)
f
v
A
=−
h
α
t
v
∗
− v
(
t
n
)
− β
∂v
∗
∂t
(
t
n
)
+ u
∗
∂v
∗
∂x
+ v
∗
∂v
∗
∂y
N
u
A
d
+
h
p
∗
∂N
u
A
∂y
d −
1
Re
h
∂u
∗
∂y
+
∂v
∗
∂x
∂N
u
A
∂x
+ 2
∂v
∗
∂y
∂N
u
A
∂y
d ,
(11.182)
f
p
B
=
h
∂u
∗
∂x
+
∂v
∗
∂y
N
p
B
d. (11.183)
The practical evaluation of the integrals in (11.175) to (11.183) is done
element-wise. We need to construct the shape functions locally and transform these
global integrals into local integrals over each element.
In the finite element method, the global shape functions have very compact sup-
port. They are zero everywhere except in the neighborhood of the corresponding grid
point in the mesh. It is convenient to cast the global formulation using the element
point of view (Section 3). In this element view, the local shape functions are defined
inside each element. The global shape functions are the assembly of the relevant local

5. Three Examples 457
ones. For example, the global shape function corresponding to the grid point A in
the finite element mesh consists of the local shape functions of all the elements that
share this grid point. An element in the physical space can be mapped into a standard
element, as shown in Figure 11.17 and the local shape functions can be defined on
this standard element. The mapping is given by
x(ξ, η) =
6
a=1
x
e
a
φ
a
(ξ, η) and y(ξ, η) =
6
a=1
y
e
a
φ
a
(ξ, η), (11.184)
where
x
e
a
,y
e
a
are the coordinates of the nodes in the element e. The local shape
functions are φ
a
. For a quadratic triangular element they are defined as
φ
1
= ζ
(
2ζ − 1
)
,φ
2
= ξ
(
2ξ − 1
)
,φ
3
= η
(
2η − 1
)
,φ
4
= 4ξζ, φ
5
= 4ξη,
φ
6
= 4ηζ, (11.185)
where ζ = 1 − ξ − η. As shown in Figure 11.17 the mapping (11.184) is able to
handle curved triangles. The variation of the flow variables within this element can
also be expressed in terms of their values at the nodes of the element and the local
shape functions,
u
=
6
a=1
u
e
a
φ
a
(
ξ,η
)
,v
=
6
a=1
v
e
a
φ
a
(
ξ,η
)
,p
=
3
b=1
p
e
b
ψ
b
(
ξ,η
)
. (11.186)
Here the shape functions for velocities are quadratic and the same as the coor-
dinates. The shape functions for the pressure are chosen to be linear, thus one order
less than those for the velocities. They are given by,
ψ
1
= ζ, ψ
2
= ξ, ψ
3
= η. (11.187)
Furthermore, the integration over the global computational domain can be written
as the summation of the integrations over all the elements in the domain. As most of
1
2
3
4
5
6
= 1 − −
(1,0,0)
(0,1,0)
(0,1/2,1/2)
(1/2,1/2,0)
1
2
3
4
5
6
x
y
(0,0,1) (1/2,0,1/2)
Ω
e
Figure 11.17 A quadratic triangular finite element mapping into the standard element.

458 Computational Fluid Dynamics
these integrations will be zero, the non-zero ones are grouped as element matrices
and vectors,
A
e
uu
=
A
euu
aa
, A
e
uv
=
A
euv
aa
, B
e
up
=
B
eup
ab
,
A
e
vu
=
A
evu
aa
, A
e
vv
=
A
evv
aa
, B
e
vp
=
B
evp
ab
, (11.188)
f
e
u
=
f
eu
a
, f
e
v
=
f
ev
a
, f
e
p
=
f
ep
b
,
where
A
euu
aa
=
e
α
t
φ
a
+ u
∗
∂φ
a
∂x
+ v
∗
∂φ
a
∂y
+
∂u
∗
∂x
φ
a
φ
a
+
1
Re
2
∂φ
a
∂x
∂φ
a
∂x
+
∂φ
a
∂y
∂φ
a
∂y
d, (11.189)
A
euv
aa
=
e
∂u
∗
∂y
φ
a
φ
a
+
1
Re
∂φ
a
∂x
∂φ
a
∂y
d, (11.190)
A
evu
aa
=
e
∂v
∗
∂x
φ
a
φ
a
+
1
Re
∂φ
a
∂y
∂φ
a
∂x
d, (11.191)
A
evv
aa
=
e
α
t
φ
a
+ u
∗
∂φ
a
∂x
+ v
∗
∂φ
a
∂y
+
∂v
∗
∂y
φ
a
φ
a
+
1
Re
∂φ
a
∂x
∂φ
a
∂x
+ 2
∂φ
a
∂y
∂φ
a
∂y
d, (11.192)
B
eup
ab
=−
e
ψ
b
∂φ
a
∂x
d, (11.193)
B
evp
ab
=−
e
ψ
b
∂φ
a
∂y
d, (11.194)
f
eu
a
=−
e
α
t
u
∗
− u
(
t
n
)
− β
∂u
∂t
(
t
n
)
+ u
∗
∂u
∗
∂x
+ v
∗
∂u
∗
∂y
φ
a
d
+
e
p
∗
∂φ
a
∂x
d −
1
Re
e
2
∂u
∗
∂x
∂φ
a
∂x
+
∂u
∗
∂y
+
∂v
∗
∂x
∂φ
a
∂y
d ,
(11.195)
f
ev
a
=−
e
α
t
v
∗
− v
(
t
n
)
− β
∂v
∗
∂t
(
t
n
)
+ u
∗
∂v
∗
∂x
+ v
∗
∂v
∗
∂y
φ
a
d
+
e
p
∗
∂φ
a
∂y
d −
1
Re
e
∂u
∗
∂y
+
∂v
∗
∂x
∂φ
a
∂x
+ 2
∂v
∗
∂y
∂φ
a
∂y
d ,
(11.196)
5. Three Examples 459
f
ep
b
=
e
∂u
∗
∂x
+
∂v
∗
∂y
ψ
b
d. (11.197)
The indices a and a
run from 1 to 6, and b and b
run from 1 to 3.
The integrals in the above expressions can be evaluated by numerical integration
rules,
e
f(x, y) d =
1
0
1−η
0
f(ξ,η)J(ξ,η)dξ dη =
1
2
N
int
l=1
f(ξ
l
,η
l
)J (ξ
l
,η
l
)W
l
,
(11.198)
where the Jacobian of the mapping (11.184) is given by J = x
ξ
y
η
− x
η
y
ξ
. Here
N
int
is the number of numerical integration points and W
l
is the weight of the lth
integration point. For this example, a seven-point integration formula with degree of
precision of 5 (see Hughes, 1987) was used.
The global matrices and vectors in (11.173) are the summations of the element
matrices and vectors in (11.188) over all the elements. In the process of summation
(assembly), a mapping of the local nodes in each element to the global node numbers
is needed. This information is commonly available for any finite element mesh.
Once the matrix equation (11.173) is generated, we may impose the essential
boundary conditions for the velocities. One simple method is to use the equation of
the boundary condition to replace the corresponding equation in the original matrix
or one can multiply a large constant by the equation of the boundary condition and
add this equation to the original system of equations in order to preserve the structure
of the matrix. The resulting matrix equation may be solved using common direct or
iterative solvers for a linear algebraic system of equations.
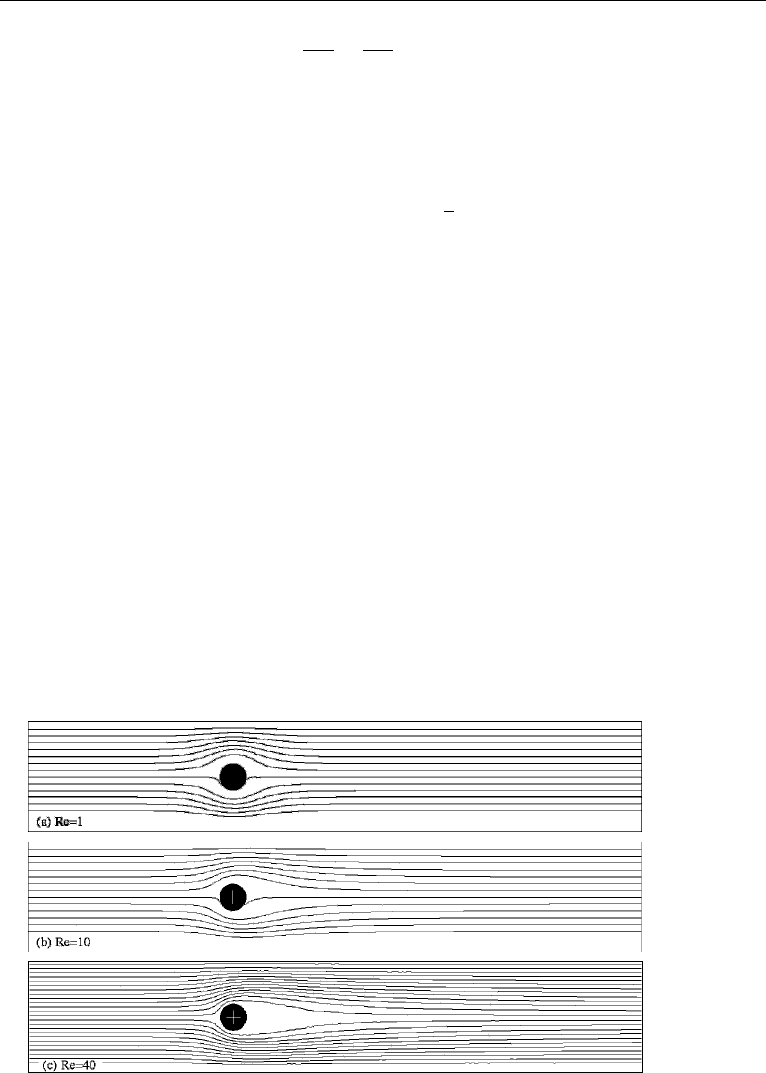
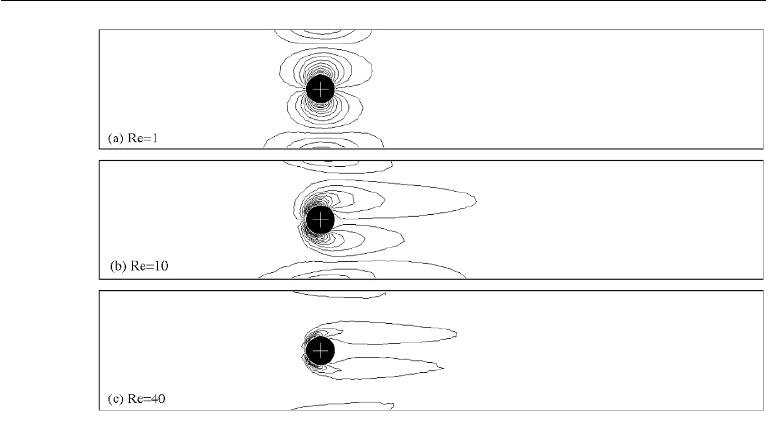
Figures 11.18 and 11.19 display the streamlines and vorticity lines around the
cylinder at three Reynolds numbers Re = 1, 10, and 40. For these Reynolds numbers,
Figure 11.18 Streamlines for flow around a cylinder at three different Reynolds numbers.
460 Computational Fluid Dynamics
Figure 11.19 Vorticity lines for flow around a cylinder at three different Reynolds numbers.
the flow is steady and should be symmetric above and below the cylinder. However,
due to the imperfection in the mesh used for the calculation and as shown in Figure
11.16, the calculated flow field is not perfectly symmetric. From Figure 11.18 we
observe the increase in the size of the wake behind the cylinder as the Reynolds
number increases. In Figure 11.19, we see the effects of the Reynolds number in the
vorticity build up in front of the cylinder, and in the convection of the vorticity by
the flow.
We next compute the case with Reynolds number Re = 100. In this case, the
flow is expected to be unsteady. Periodic vortex shedding occurs. In order to capture
the details of the flow, we used a finer mesh than the one shown in Figure 11.16. The
finer mesh has 9222 elements, 18816 velocity nodes and 4797 pressure nodes. In this
calculation, the flow starts from rest. Initially, the flow is symmetric, and the wake
behind the cylinder grows bigger and stronger. Then, the wake becomes unstable,
undergoes a supercritical Hopf bifurcation, and sheds periodically away from the
cylinder. The periodic vortex shedding forms the well-known von Karman vortex
street. The vorticity lines are presented in Figure 11.20 for a complete cycle of vortex
shedding.
For this case with Re = 100, we plot in Figure 11.21 the history of the forces and
torque acting on the cylinder. The oscillations shown in the lift and torque plots are
typical for the supercritical Hopf bifurcation. The nonzero mean value of the torque
shown in Figure 11.21c is due to the asymmetry in the finite element mesh. It is clear
that the flow becomes fully periodic at the times shown in Figure 11.20. The period of
the oscillation is measured as τ = 0.0475s or ¯τ = 4.75 in the non-dimensional units.
This period corresponds to a nondimensional Strouhal number S = nd
/
U = 0.21,
where n is the frequency of the shedding. In the literature, the value of the Strouhal
number for an unbounded uniform flow around a cylinder is found to be around 0.167

6. Concluding Remarks 461
Figure 11.20 Vorticity lines for flow around a cylinder at Reynolds number Re = 100.
¯
t = tU/d is the
dimensionless time.
at Re = 100 (e.g., see Wen and Lin, 2001). The difference could be caused by the
geometry in which the cylinder is confined in a channel.
6. Concluding Remarks
It should be strongly emphasized that CFD is merely a tool for analyzing fluid-flow
problems. If it is used correctly, it would provide useful information cheaply and
quickly. However, it could easily be misused or even abused. In today’s computer
age, people have a tendency to trust the output from a computer, especially when they
do not understand what is behind the computer. One certainly should be aware of the
assumptions used in producing the results from a CFD model.
As we have previously discussed, CFD is never exact. There are uncertainties
involved in CFD predictions. However, one is able to gain more confidence in CFD
predictions by following a few steps. Tests on some benchmark problems with known
solutions are often encouraged. A mesh refinement test is normally a must in order
