Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

462 Computational Fluid Dynamics

t = t ⋅ U d

20.006

0 20 40 60 80 100 120

20.004

20.002

0.002

0.004

0.006

Torque

(c)

(a)

1.88

20 40 60 80

1.9

1.92

1.94

1.96

1.98

2.02

100 120

t = t ⋅ U d

Drag

t = t ⋅ U d

20.5

20 40 60 80 100 1200

0.5

0 0475s

(b)

ρU

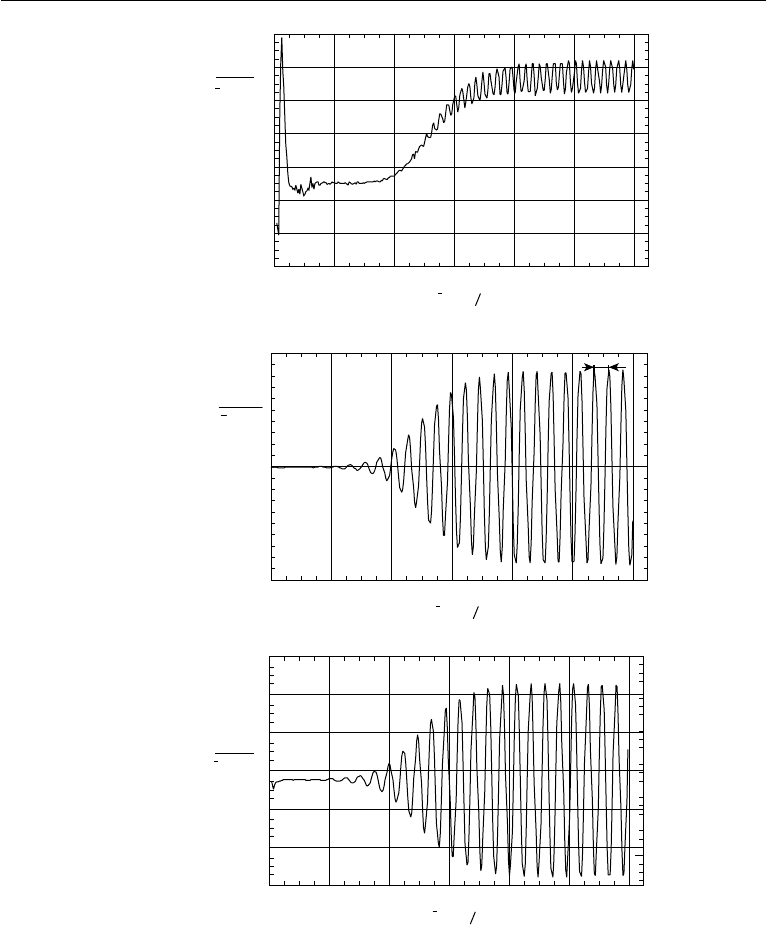
Figure 11.21 History of forces and torque acting on the cylinder at Re = 100: (a) drag coefﬁcient; (b) lift

coefﬁcient; and (c) coefﬁcient for the torque.

6. Concluding Remarks 463

to be sure that the numerical solution converges to something meaningful. A similar

test with the time step for unsteady ﬂow problems is often desired. If the boundary

locations and conditions are in doubt, their effects on the CFD predictions should be

minimized. Furthermore, the sensitivity of the CFD predictions to some key param-

eters in the problem should be investigated for practical design problems.

In this chapter, we have discussed the basics of the ﬁnite difference and ﬁnite

element methods and their applications in CFD. There are other kinds of numer-

ical methods, for example, the spectral method and the spectral element method,

which are often used in CFD. They share the common approach that discretizes

the Navier-Stokes equations into a system of algebraic equations. However, a class

of new numerical techniques including lattice gas cellular automata, lattice Boltz-

mann method, and dissipative particle dynamics do not start from the continuum

Navier-Stokes equations. Unlike the conventional methods discussed in this chapter,

they are based on simpliﬁed kinetic models that incorporate the essential physics of

the microscopic or mesoscopic processes so that the macroscopic-averaged properties

obey the desired macroscopic Navier-Stokes equations.

Exercises

1. Show that the stability condition for the explicit scheme (11.10) is the condition

(11.26).

2. For the heat conduction equation ∂T

∂t − D



∂

∂x



= 0, one of the

discretized forms is

−sT

n+1

j+1

(

1 + 2s

)

n+1

− sT

n+1

j−1

= T

where s = Dt

x

. Show that this implicit algorithm is always stable.

3. An insulated rod initially has a temperature of T

(

x,0

)

= 0

◦

(

0  x  1

)

At t = 0 hot reservoirs

(

T = 100

◦

)

are brought into contact with the two ends,

(

x = 0

)

and B

(

x = 1

)

: T

(

0,t

)

= T

(

1,t

)

= 100

◦

C. Numerically ﬁnd the tem-

perature T

(

x,t

)

of any point in the rod. The governing equation of the problem is

the heat conduction equation ∂T

∂t − D



∂

∂x



= 0. The exact solution to this

problem is

∗





= 100 −



m=1

400

(

2m − 1

)

sin



(

2m − 1

)

πx



exp



−D

(

2m − 1

)



(11.199)

where M is the number of terms used in the approximation.

(a). Try to solve the problem with the explicit forward time, centered space

(FTCS) scheme. Use the parameter s = Dt

x

=0.5 and 0.6 to test the stability of

the scheme.

464 Computational Fluid Dynamics

(b). Solve the problem with a stable explicit or implicit scheme. Test the rate of

convergence numerically using the error atx = 0.5.

4. Derive the weak form, Galerkin form, and the matrix form of the following

strong problem:

Given functions D(x), f (x), and constants g, h, ﬁnd u(x) such that

[D(x)u

]

+ f(x)= 0on = (0, 1),

with u(0) = g and − u

(1) = h.

Write a computer program solving this problem using piecewise-linear shape

functions. You may set D = 1, g = 1, h = 1 and h = 1. Check your numerical result

with the exact solution.

5. Solve numerically the steady convective transport equation,

∂T

∂x

= D

∂

∂x

, for 0  x  1,

with two boundary conditions T(0) = 0 and T(1) = 1, where u and D are two

constants,

(a) using the centered ﬁnite difference scheme in equation (11.91), and compare with

the exact solution; and

(b) using the upwind scheme (11.93), and compare with the exact solution.

6. Code the explicit MacCormack scheme with the FF/BB arrangement for the

driven cavity ﬂow problem as described in Section 5. Compute the ﬂow ﬁeld at

Re = 100 and 400, and explore effects of Mach number and the stability condition

(11.110).

Literature Cited

Brooks, A. N. and T. J. R. Hughes (1982). “Streamline-upwinding/Petrov-Galerkin formulation for convec-

tion dominated ﬂows with particular emphasis on incompressible Navier-Stokes equation.” Comput.

Methods Appl. Mech. Engrg. 30: 199–259.

Chorin, A. J. (1967). “A numerical method for solving incompressible viscous ﬂow problems.” J. Comput.

Phys. 2: 12–26.

Chorin, A. J. (1968). “Numerical solution of the Navier-Stokes equations.” Math. Comput. 22: 745–762.

Dennis, S. C. R. and G. Z. Chang (1970). “Numerical solutions for steady ﬂow past a circular cylinder at

Reynolds numbers up to 100.” J. Fluid Mech. 42: 471–489.

Fletcher, C. A. J. (1988). Computational Techniques for Fluid Dynamics, I–Fundamental and General

Techniques, and II–Special Techniques for Different Flow Categories, New York: Springer-Verlag.

Franca, L. P., S. L. Frey and T. J. R. Hughes (1992). “Stabilized ﬁnite element methods: I. Application to

the advective-diffusive model.” Comput. Methods Appl. Mech. Engrg. 95: 253–276.

Franca, L. P. and S. L. Frey (1992). “Stabilized ﬁnite element methods: II. The incompressible

Navier-Stokes equations,”Comput. Methods Appl. Mech. Engrg. 99: 209–233.

Ghia, U., K. N. Ghia, C. T. Shin (1982)

ıHigh-Re solutions for incompressible ﬂow using the Navier-Stokes

equations and a multigrid method.

ı J. Comput. Phys. 48: 387–411.

Glowinski, R. (1991). “Finite element methods for the numerical simulation of incompressible viscous

ﬂow, introduction to the control of the Navier-Stokes equations,” in Lectures in Applied Mathematics

Vol.28: 219–301. Providence, R.I.: American Mathematical Society.

Literature Cited 465

Gresho, P. M. (1991). “Incompressible ﬂuid dynamics: Some fundamental formulation issues,” Annu. Rev.

Fluid Mech. 23: 413–453.

Harlow, F. H. and J. E. Welch (1965). “Numerical calculation of time-dependent viscous incompressible

ﬂow of ﬂuid with free surface.” Phys. Fluids 8: 2182–2189.

Hou, S., Q. Zou, S. Chen, G. D. Doolen and A. C. Cogley (1995).

ıSimulation of cavity ﬂow by the lattice

Boltzmann method.

ı J. Comp. Phys. 118: 329–347.

Hughes, T. J. R. (1987). The Finite Element Method, Linear Static and Dynamic Finite Element Analysis,

Englewood Cliffs, NJ: Prentice-Hall.

MacCormack, R. W. (1969). “The effect of viscosity in hypervelocity impact cratering.” AIAA Paper

69–354, Cincinnati, Ohio.

Marchuk, G. I. (1975). Methods of Numerical Mathematics, New York: Springer-Verlag.

Noye, J (1983). Chapter 2 in Numerical Solution of Differential Equations, J. Noye, ed., Amsterdam:

North-Holland.

Oden, J. T. and G. F. Carey (1984). Finite Elements: Mathematical Aspects, Vol. IV, Englewood Cliffs,

N.J.: Prentice-Hall.

Perrin, A. and H.H. Hu (2006). “An explicit ﬁnite-difference scheme for simulation of moving particles,”

J. Comput. Phys. 212: 166–187.

Peyret, R. and T. D. Taylor (1983). Computational Methods for Fluid Flow, New York: Springer-Verlag.

Richtmyer, R. D. and K. W. Morton (1967). Difference Methods for Initial-Value Problems, New York:

Interscience.

Saad, Y. (1996). Iterative Methods for Sparse Linear Systems, Boston: PWS Publishing Company.

Sucker, D. and H. Brauer (1975). “Fluiddynamik bei der angestr

omten Zylindern.” W

arme-Stoff¨ubertrag.

8: 149.

Takami, H. and H. B. Keller (1969). “Steady two-dimensional viscous ﬂow of an incompressible ﬂuid past

a circular cylinder.” Phys. Fluids 12: Suppl.II, II-51-II-56.

Tannehill, J. C., D. A. Anderson, R. H. Pletcher (1997), Computational Fluid Mechanics and Heat Transfer,

Washington, DC, Taylor & Francis.

Temam, R. (1969). “Sur l’approximation des

equations de Navier-Stokes par la m

ethode de pas fraction-

aires.” Archiv. Ration. Mech. Anal. 33: 377–385.

Tezduyar, T. E. (1992). “Stabilized Finite Element Formulations for Incompressible Flow Computations,”

in Advances in Applied Mechanics , J.W. Hutchinson and T.Y. Wu eds., Vol. 28: 1–44. New York:

Academic Press.

Yanenko, N. N. (1971). The Method of Fractional Steps, New York: Springer-Verlag.

Wen, C. Y. and C. Y. Lin (2001). “Two dimensional vortex shedding of a circular cylinder,” Phys. Fluids

13: 557–560.

This page intentionally left blank

Chapter 12

Instability

1. Introduction......................... 467

2. Method of Normal Modes ............ 469

3. Thermal Instability: The B´enard

Problem............................. 470

Formulation of the Problem ......... 471

Proof That σ Is Real for Ra > 0 ...... 475

Solution of the Eigenvalue Problem

with Two Rigid Plates ............. 477

Solution with Stress-Free Surfaces . . . 480

Cell Patterns ........................ 481

4. Double-Diffusive Instability .......... 482

Finger Instability .................... 482

Oscillating Instability ................ 485

5. Centrifugal Instability:

Taylor Problem ..................... 486

Rayleigh’s Inviscid Criterion ......... 486

Formulation of the Problem ......... 488

Discussion of Taylor’s Solution ....... 490

6. Kelvin–Helmholtz Instability ......... 493

7. Instability of Continuously

Stratiﬁed Parallel Flows ............. 500

Taylor–Goldstein Equation .......... 500

Richardson Number Criterion........ 503

Howard’s Semicircle Theorem ....... 504

8. Squire’s Theorem and

Orr–Sommerfeld Equation ........... 507

Squire’s Theorem.................... 509

Orr–Sommerfeld Equation........... 509

9. Inviscid Stability of Parallel Flows . . 510

Rayleigh’s Inﬂection Point Criterion . 511

Fjortoft’s Therorm ................. 511

Critical Layers ..................... 512

10. Some Results of Parallel Viscous

Flows .............................. 514

Mixing Layer ...................... 515

Plane Poiseuille Flow ............... 516

Plane Couette Flow................. 516

Pipe Flow .......................... 516

Boundary Layers with Pressure

Gradients ........................ 517

How can Viscosity Destabilize a

Flow? ........................... 519

11. Experimental Veriﬁcation of

Boundary Layer Instability ......... 520

12. Comments on Nonlinear Effects ..... 522

13. Transition .......................... 523

14. Deterministic Chaos ................ 525

Phase Space ....................... 526

Attractor........................... 527

The Lorenz Model of Thermal

Convection ...................... 528

Strange Attractors .................. 530

Scenarios for Transition to Chaos . . . 531

Closure ............................ 533

Exercises ........................... 533

Literature Cited .................... 535

1. Introduction

A phenomenon that may satisfy all conservation laws of nature exactly, may still

be unobservable. For the phenomenon to occur in nature, it has to satisfy one more

condition, namely, it must be stable to small disturbances. In other words, inﬁnitesi-

mal disturbances, which are invariably present in any real system, must not amplify

467

DOI: 10.1016/B978-0-12-381399-2.50012-5

468 Instability

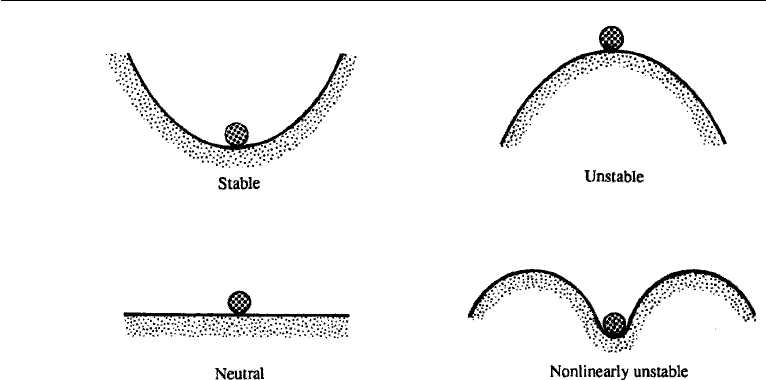
Figure 12.1 Stable and unstable systems.

spontaneously. A perfectly vertical rod satisﬁes all equations of motion, but it does

not occur in nature. A smooth ball resting on the surface of a hemisphere is stable (and

therefore observable) if the surface is concave upwards, but unstable to small displace-

ments if the surface is convex upwards (Figure 12.1). In ﬂuid ﬂows, smooth laminar

ﬂows are stable to small disturbances only when certain conditions are satisﬁed. For

example, in ﬂows of homogeneous viscous ﬂuids in a channel, the Reynolds number

must be less than some critical value, and in a stratiﬁed shear ﬂow, the Richardson

number must be larger than a critical value. When these conditions are not satisﬁed,

inﬁnitesimal disturbances grow spontaneously. Sometimes the disturbances can grow

to a ﬁnite amplitude and reach equilibrium, resulting in a new steady state. The new

state may then become unstable to other types of disturbances, and may grow to yet

another steady state, and so on. Finally, the ﬂow becomes a superposition of various

large disturbances of random phases, and reaches a chaotic condition that is com-

monly described as “turbulent.” Finite amplitude effects, including the development

of chaotic solutions, will be examined brieﬂy later in the chapter.

The primary objective of this chapter, however, is the examination of stability

of certain ﬂuid ﬂows with respect to inﬁnitesimal disturbances. We shall introduce

perturbations on a particular ﬂow, and determine whether the equations of motion

demand that the perturbations should grow or decay with time. In this analysis the

problem is linearized by neglecting terms quadratic in the perturbation variables

and their derivatives. This linear method of analysis, therefore, only examines the

initial behavior of the disturbances. The loss of stability does not in itself constitute

a transition to turbulence, and the linear theory can at best describe only the very

beginning of the process of transition to turbulence. Moreover, a real ﬂow may be

stable to inﬁnitesimal disturbances (linearly stable), but still can be unstable to sufﬁ-

ciently large disturbances (nonlinearly unstable); this is schematically represented in

Figure 12.1. These limitations of the linear stability analysis should be kept in mind.

2. Method of Normal Modes 469

Nevertheless, the successes of the linear stability theory have been considerable.

For example, there is almost an exact agreement between experiments and theoretical

prediction of the onset of thermal convection in a layer of ﬂuid, and of the onset of

the Tollmien–Schlichting waves in a viscous boundary layer. Taylor’s experimental

veriﬁcation of his own theoretical prediction of the onset of secondary ﬂow in a

rotating Couette ﬂow is so striking that it has led people to suggest that Taylor’s

work is the ﬁrst rigorous conﬁrmation of Navier–Stokes equations, on which the

calculations are based.

For our discussion we shall choose problems that are of importance in geophysical

as well as engineering applications. None of the problems discussed in this chapter,

however, contains Coriolis forces; the problem of “baroclinic instability,” which does

contain the Coriolis frequency, is discussed in Chapter 14. Some examples will also

be chosen to illustrate the basic physics rather than any potential application. Further

details of these and other problems can be found in the books by Chandrasekhar

(1961, 1981) and Drazin and Reid (1981). The review article by Bayly, Orszag, and

Herbert (1988) is recommended for its insightful discussions after the reader has read

this chapter.

2. Method of Normal Modes

The method of linear stability analysis consists of introducing sinusoidal disturbances

on a basic state (also called background or initial state), which is the ﬂow whose

stability is being investigated. For example, the velocity ﬁeld of a basic state involving

a ﬂow parallel to the x-axis, and varying along the y-axis, is U =[U(y),0, 0 ].On

this background ﬂow we superpose a disturbance of the form

u(x,t) =ˆu( y) e

ikx+imz+σt

, (12.1)

where ˆu(y) is a complex amplitude; it is understood that the real part of the right-hand

side is taken to obtain physical quantities. (The complex form of notation is explained

in Chapter 7, Section 15.) The reason solutions exponential in (x,z,t) are allowed

in equation (12.1) is that, as we shall see, the coefﬁcients of the differential equation

governing the perturbation in this ﬂow are independent of (x,z,t). The ﬂow ﬁeld is

assumed to be unbounded in the x and z directions, hence the wavenumber components

k and m can only be real in order that the dependent variables remain bounded as x,

z →∞; σ = σ

+ iσ

is regarded as complex.

The behavior of the system for all possible K =[k, 0,m] is examined in the

analysis. If σ

is positive for any value of the wavenumber, the system is unstable to

disturbances of this wavenumber. If no such unstable state can be found, the system

is stable. We say that

< 0: stable,

> 0: unstable,

= 0: neutrally stable.

470 Instability

The method of analysis involving the examination of Fourier components such as

equation (12.1) is called the normal mode method. An arbitrary disturbance can be

decomposed into a complete set of normal modes. In this method the stability of each

of the modes is examined separately, as the linearity of the problem implies that the var-

ious modes do not interact. The method leads to an eigenvalue problem, as we shall see.

The boundary between stability and instability is called the marginal state, for

which σ

= 0. There can be two types of marginal states, depending on whether σ

also zero or nonzero in this state. If σ

= 0 in the marginal state, then equation (12.1)

shows that the marginal state is characterized by a stationary pattern of motion;

we shall see later that the instability here appears in the form of cellular convection or

secondary ﬂow (see Figure 12.12 later). For such marginal states one commonly says

that the principle of exchange of stabilities is valid. (This expression was introduced

by Poincar´e and Jeffreys, but its signiﬁcance or usefulness is not entirely clear.)

If, on the other hand, σ

= 0 in the marginal state, then the instability sets in as

oscillations of growing amplitude. Following Eddington, such a mode of instability

is frequently called “overstability” because the restoring forces are so strong that the

system overshoots its corresponding position on the other side of equilibrium. We

prefer to avoid this term and call it the oscillatory mode of instability.

The difference between the neutral state and the marginal state should be noted

as both have σ

= 0. However, the marginal state has the additional constraint that it

lies at the borderline between stable and unstable solutions. That is, a slight change

of parameters (such as the Reynolds number) from the marginal state can take the

system into an unstable regime where σ

> 0. In many cases we shall ﬁnd the stability

criterion by simply setting σ

= 0, without formally demonstrating that it is indeed

at the borderline of unstable and stable states.

3. Thermal Instability: The B´enard Problem

A layer of ﬂuid heated from below is “top heavy,” but does not necessarily undergo

a convective motion. This is because the viscosity and thermal diffusivity of the

ﬂuid try to prevent the appearance of convective motion, and only for large enough

temperature gradients is the layer unstable. In this section we shall determine the

condition necessary for the onset of thermal instability in a layer of ﬂuid.

The ﬁrst intensive experiments on instability caused by heating a layer of ﬂuid

were conducted by B´enard in 1900. B´enard experimented on only very thin layers

(a millimeter or less) that had a free surface and observed beautiful hexagonal cells

when the convection developed. Stimulated by these experiments, Rayleigh in 1916

derived the theoretical requirement for the development of convective motion in a

layer of ﬂuid with two free surfaces. He showed that the instability would occur when

the adverse temperature gradient was large enough to make the ratio

Ra =

gαd

κν

(12.2)

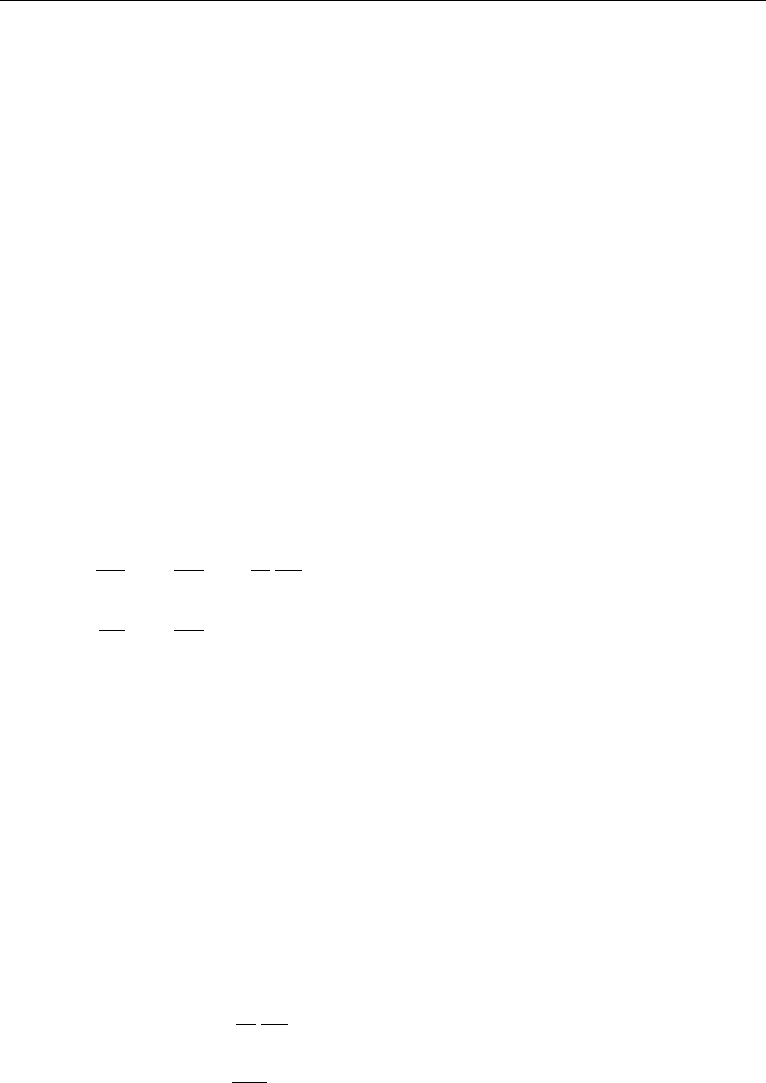
3. Thermal Instability: The B´enard Problem 471

exceed a certain critical value. Here, g is the acceleration due to gravity, α is the

coefﬁcient of thermal expansion,  =−d

T/dz is the vertical temperature gradient

of the background state, d is the depth of the layer, κ is the thermal diffusivity, and ν is

the kinematic viscosity. The parameter Ra is called the Rayleigh number, and we shall

see shortly that it represents the ratio of the destabilizing effect of buoyancy force to

the stabilizing effect of viscous force. It has been recognized only recently that most

of the motions observed by B´enard were instabilities driven by the variation of surface

tension with temperature and not the thermal instability due to a top-heavy density

gradient (Drazin and Reid 1981, p. 34). The importance of instabilities driven by

surface tension decreases as the layer becomes thicker. Later experiments on thermal

convection in thicker layers (with or without a free surface) have obtained convective

cells of many forms, not just hexagonal. Nevertheless, the phenomenon of thermal

convection in a layer of ﬂuid is still commonly called the B´enard convection.

Rayleigh’s solution of the thermal convection problem is considered a major

triumph of the linear stability theory. The concept of critical Rayleigh number ﬁnds

application in such geophysical problems as solar convection, cloud formation in the

atmosphere, and the motion of the earth’s core.

Formulation of the Problem

Consider a layer conﬁned between two isothermal walls, in which the lower wall is

maintained at a higher temperature. We start with the Boussinesq set

∂ ˜u

∂t

+˜u

∂ ˜u

∂x

=−

∂ ˜p

∂x

− g[1 − α(

T − T

)]δ

+ ν∇

˜u

∂

∂t

+˜u

∂

∂x

= κ∇

(12.3)

along with the continuity equation ∂ ˜u

/∂x

= 0. Here, the density is given by the

equation of state ˜ρ = ρ

[1 − α(

T − T

)], with ρ

representing the reference density

at the reference temperature T

. The total ﬂow variables (background plus perturba-

tion) are represented by a tilde ( ˜), a convention that will also be used in the follow-

ing chapter. We decompose the motion into a background state of no motion, plus

perturbations:

˜u

= 0 + u

(x,t),

T =

T(z)+ T



(x,t),

˜p = P(z)+ p(x,t),

(12.4)

where the z-axis is taken vertically upward. The variables in the basic state are

represented by uppercase letters except for the temperature, for which the symbol is

T .

The basic state satisﬁes

0 =−

∂P

∂x

− g[1 − α(

T − T

)]δ

0 = κ

(12.5)