Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

492 Instability

Figure 12.12 Instability of rotating Couette ﬂow. Panels a, b, c, and d correspond to increasing Taylor

number. D. Coles, Journal of Fluid Mechanics 21: 385–425, 1965 and reprinted with the permission of

Cambridge University Press.

annulus. More complicated patterns of vortices result at a higher rates of rotation,

ﬁnally resulting in the occasional appearance of turbulent patches (Figure 12.12d),

and then a fully turbulent ﬂow.

Phenomena analogous to the Taylor vortices are called secondary ﬂows because

they are superposed on a primary ﬂow (such as the Couette ﬂow in the present case).

6. Kelvin–Helmholtz Instability 493

Figure 12.13 G¨ortler vortices in a boundary layer along a concave wall.

There are two other situations where a combination of curved streamlines (which

give rise to centrifugal forces) and viscosity result in instability and steady secondary

ﬂows in the form of vortices. One is the ﬂow through a curved channel, driven by

a pressure gradient. The other is the appearance of G¨ortler vortices in a bound-

ary layer ﬂow along a concave wall (Figure 12.13). The possibility of secondary

ﬂows signiﬁes that the solutions of the Navier–Stokes equations are nonunique in

the sense that more than one steady solution is allowed under the same boundary

conditions. We can derive the form of the primary ﬂow only if we exclude the sec-

ondary ﬂow by appropriate assumptions. For example, we can derive the expression

(12.36) for Couette ﬂow by assuming that U

= 0 and U

= 0, which rule out the

secondary ﬂow.

6. Kelvin–Helmholtz Instability

Instability at the interface between two horizontal parallel streams of different

velocities and densities, with the heavier ﬂuid at the bottom, is called the

Kelvin–Helmholtz instability. The name is also commonly used to describe the insta-

bility of the more general case where the variations of velocity and density are con-

tinuous and occur over a ﬁnite thickness. The more general case is discussed in the

following section.

Assume that the layers have inﬁnite depth and that the interface has zero thickness.

Let U

and ρ

be the velocity and density of the basic state in the upper layer and U

and ρ

be those in the bottom layer (Figure 12.14). By Kelvin’s circulation theorem,

the perturbed ﬂow must be irrotational in each layer because the motion develops from

an irrotational basic ﬂow of uniform velocity in each layer. The ﬂow can therefore be

described by a velocity potential that satisﬁes the Laplace equation. Let the variables

in the perturbed state be denoted by a tilde ( ˜). Then

∇

= 0, ∇

= 0. (12.42)

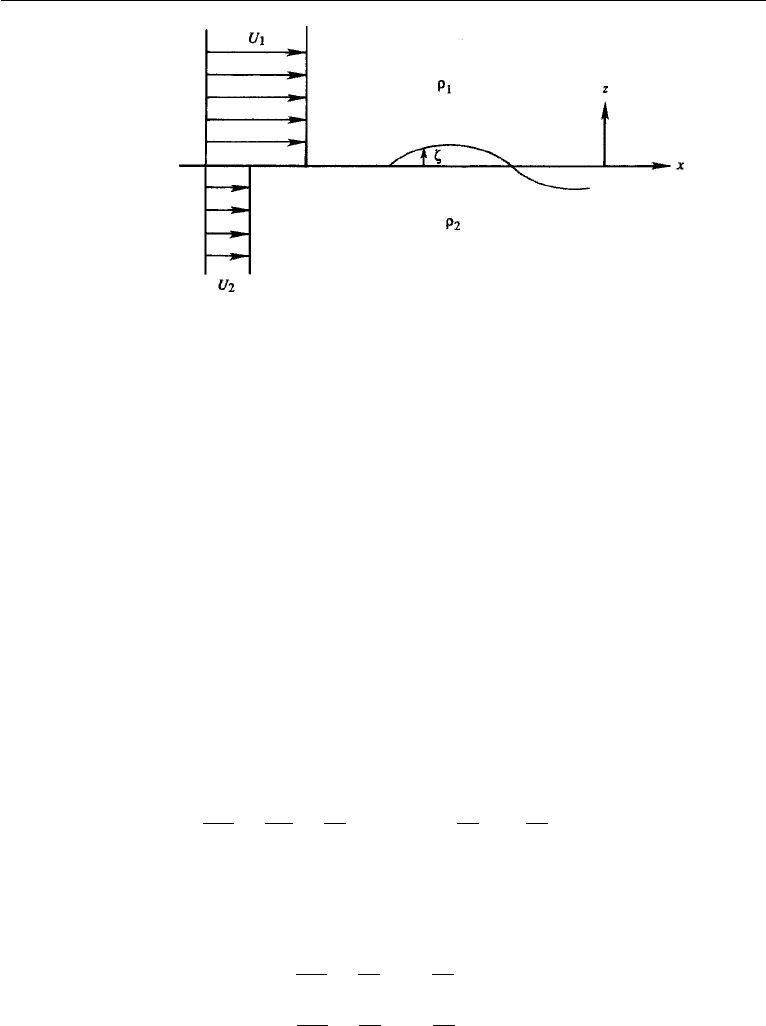
494 Instability

Figure 12.14 Discontinuous shear across a density interface.

The ﬂow is decomposed into a basic state plus perturbations:

= U

x + φ

= U

x + φ

(12.43)

where the ﬁrst terms on the right-hand side represent the basic ﬂow of uniform streams.

Substitution into equation (12.42) gives the perturbation equations

∇

= 0, ∇

= 0, (12.44)

subject to

→ 0asz →∞,

→ 0asz →−∞.

(12.45)

As discussed in Chapter 7, there are kinematic and dynamic conditions to be

satisﬁed at the interface. The kinematic boundary condition is that the ﬂuid particles

at the interface must move with the interface. Considering particles just above the

interface, this requires

∂φ

∂z

Dζ

∂ζ

∂t

+ (U

+ u

)

∂ζ

∂x

+ v

∂ζ

∂y

at z = ζ.

This condition can be linearized by applying it at z = 0 instead of at z = ζ and

by neglecting quadratic terms. Writing a similar equation for the lower layer, the

kinematic boundary conditions are

∂φ

∂z

∂ζ

∂t

+ U

∂ζ

∂x

at z = 0, (12.46)

∂φ

∂z

∂ζ

∂t

+ U

∂ζ

∂x

at z = 0. (12.47)

The dynamic boundary condition at the interface is that the pressure must be

continuous across the interface (if surface tension is neglected), requiring p

= p

6. Kelvin–Helmholtz Instability 495

at z = ζ . The unsteady Bernoulli equations are

∂

∂t

(∇

)

˜p

+ gz = C

∂

∂t

(∇

)

˜p

+ gz = C

(12.48)

In order that the pressure be continuous in the undisturbed state (P

= P

at z = 0),

the Bernoulli equation requires



− C



= ρ



− C



. (12.49)

Introducing the decomposition (12.43) into the Bernoulli equations (12.48), and

requiring ˜p

=˜p

at z = ζ , we obtain the following condition at the interface:

− ρ

∂φ

∂t

−

[(U

+ u

)

+ v

+ w

]−ρ

gζ

= ρ

− ρ

∂φ

∂t

−

[(U

+ u

)

+ v

+ w

]−ρ

gζ.

Subtracting the basic state condition (12.49) and neglecting nonlinear terms, we obtain



∂φ

∂t

+ U

∂φ

∂x

+ gζ



z=0

= ρ



∂φ

∂t

+ U

∂φ

∂x

+ gζ



z=0

. (12.50)

The perturbations therefore satisfy equation (12.44), and conditions (12.45),

(12.46), (12.47), and (12.50). Assume normal modes of the form

(ζ, φ

,φ

) = (

ζ,

ik(x−ct)

where k is real (and can be taken positive without loss of generality), but c = c

+ ic

is complex. The ﬂow is unstable if there exists a positive c

. (Note that in the preceding

sections we assumed a time dependence of the form exp(σt), which is more convenient

when the instability appears in the form of convective cells.) Substitution of the normal

modes into the Laplace equations (12.44) requires solutions of the form

= Ae

−kz

= Be

where solutions exponentially increasing from the interface are ignored because of

equation (12.45).

Now equations (12.46), (12.47), and (12.50) give three homogeneous linear alge-

braic equations for determining the three unknowns

ζ , A, and B; solutions can

496 Instability

therefore exist only for certain values of c(k). The kinematic conditions (12.46)

and (12.47) give

A =−i(U

− c)

ζ,

B = i(U

− c)

ζ.

The Bernoulli equation (12.50) gives

[ik(U

− c)A + g

ζ ]=ρ

[ik(U

− c)B + g

ζ ].

Substituting for A and B, this gives the eigenvalue relation for c(k):

kρ

− c)

+ kρ

− c)

= g(ρ

− ρ

for which the solutions are

c =

+ ρ



− ρ

+ ρ

− ρ



− U

+ ρ





1/2

. (12.51)

It is seen that both solutions are neutrally stable (c real) as long as the second term

within the square root is smaller than the ﬁrst; this gives the stable waves of the

system. However, there is a growing solution (c

> 0) if

g(ρ

− ρ

)<kρ

− U

)

Equation (12.51) shows that for each growing solution there is a corresponding decay-

ing solution. As explained more fully in the following section, this happens because

the coefﬁcients of the differential equation and the boundary conditions are all real.

Note also that the dispersion relation of free waves in an initial static medium, given

by Equation (7.105), is obtained from equation (12.51) by setting U

= U

= 0.

If U

= U

, then one can always ﬁnd a large enough k that satisﬁes the require-

ment for instability. Because all wavelengths must be allowed in an instability analysis,

we can say that the ﬂow is always unstable (to short waves) if U

= U

Consider now the ﬂow of a homogeneous ﬂuid (ρ

= ρ

) with a velocity dis-

continuity, which we can call a vortex sheet. Equation (12.51) gives

c =

+ U

) ±

− U

The vortex sheet is therefore always unstable to all wavelengths. It is also seen that

the unstable wave moves with a phase velocity equal to the average velocity of the

basic ﬂow. This must be true from symmetry considerations. In a frame of refer-

ence moving with the average velocity, the basic ﬂow is symmetric and the wave

therefore should have no preference between the positive and negative x directions

(Figure 12.15).

The Kelvin–Helmholtz instability is caused by the destabilizing effect of shear,

which overcomes the stabilizing effect of stratiﬁcation. This kind of instability is easy

6. Kelvin–Helmholtz Instability 497

Figure 12.15 Background velocity ﬁeld as seen by an observer moving with the average velocity

+ U

)/2 of two layers.

Figure 12.16 Kelvin–Helmholtz instability generated by tilting a horizontal channel containing two

liquids of different densities. The lower layer is dyed. Mean ﬂow in the lower layer is down the plane and

that in the upper layer is up the plane. S. A. Thorpe, Journal of Fluid Mechanics 46: 299–319, 1971 and

reprinted with the permission of Cambridge University Press.

to generate in the laboratory by ﬁlling a horizontal glass tube (of rectangular cross

section) containing two liquids of slightly different densities (one colored) and gently

tilting it. This starts a current in the lower layer down the plane and a current in the

upper layer up the plane. An example of instability generated in this manner is shown

in Figure 12.16.

Shear instability of stratiﬁed ﬂuids is ubiquitous in the atmosphere and the ocean

and believed to be a major source of internal waves in them. Figure 12.17 is a striking

photograph of a cloud pattern, which is clearly due to the existence of high shear across

a sharp density gradient. Similar photographs of injected dye have been recorded in

oceanic thermoclines (Woods, 1969).

498 Instability

Figure 12.17 Billow cloud near Denver, Colorado. P. G. Drazin and W. H. Reid, Hydrodynamic Stability,

1981 and reprinted with the permission of Cambridge University Press.

Figures 12.16 and 12.17 show the advanced nonlinear stage of the instability in

which the interface is a rolled-up layer of vorticity. Such an observed evolution of the

interface is in agreement with results of numerical calculations in which the nonlinear

terms are retained (Figure 12.18).

The source of energy for generating the Kelvin–Helmholtz instability is derived

from the kinetic energy of the shear ﬂow. The disturbances essentially smear out the

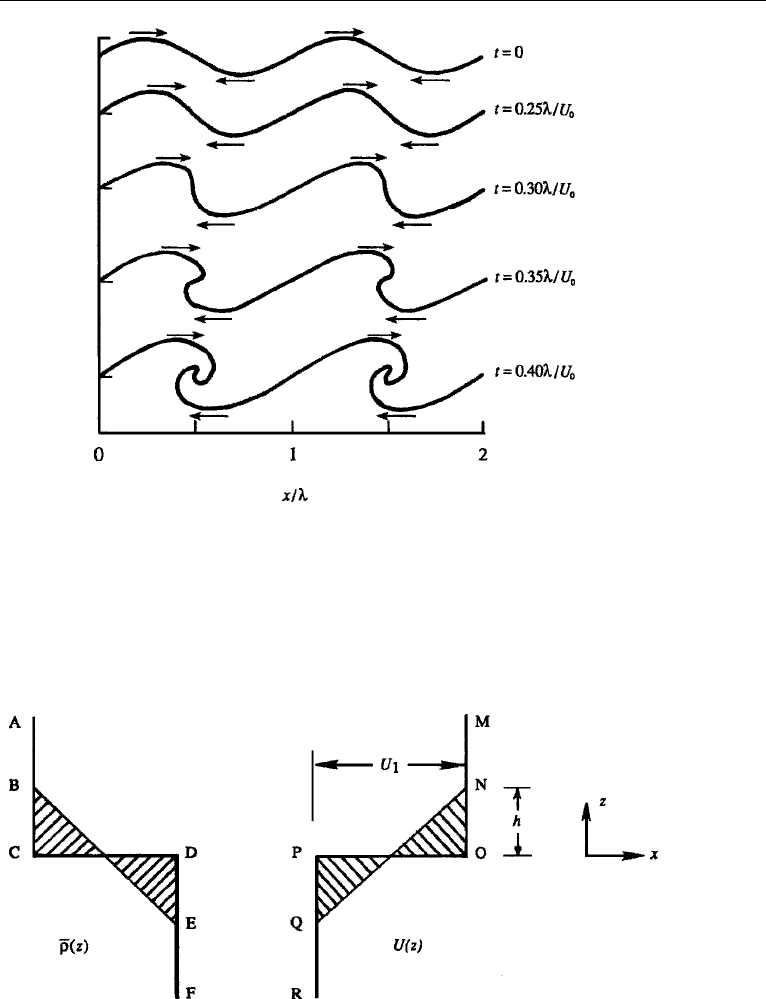
gradients until they cannot grow any longer. Figure 12.19 shows a typical behavior, in

which the unstable waves at the interface have transformed the sharp density proﬁle

ACDF to ABEF and the sharp velocity proﬁle MOPR to MNQR. The high-density

ﬂuid in the depth range DE has been raised upward (and mixed with the lower-density

ﬂuid in the depth range BC), which means that the potential energy of the system has

increased after the instability. The required energy has been drawn from the kinetic

energy of the basic ﬁeld. It is easy to show that the kinetic energy of the initial proﬁle

MOPR is larger than that of the ﬁnal proﬁle MNQR. To see this, assume that the

initial velocity of the lower layer is zero and that of the upper layer is U

. Then the

linear velocity proﬁle after mixing is given by

U(z) = U





− h  z  h.

6. Kelvin–Helmholtz Instability 499

Figure 12.18 Nonlinear numerical calculation of the evolution of a vortex sheet that has been given a

small sinusoidal displacement of wavelength λ. The density difference across the interface is zero, and U

is the velocity difference across the sheet. J. S. Turner, Buoyancy Effects in Fluids, 1973 and reprinted with

the permission of Cambridge University Press.

Figure 12.19 Smearing out of sharp density and velocity proﬁles, resulting in an increase of potential

energy and a decrease of kinetic energy.

500 Instability

Consider the change in kinetic energy only in the depth range −h<z<h, as the

energy outside this range does not change. Then the initial and ﬁnal kinetic energies

per unit width are

initial

ﬁnal



−h

(z) dz =

The kinetic energy of the ﬂow has therefore decreased, although the total momentum



Udz) is unchanged. This is a general result: If the integral of U(z) does not

change, then the integral of U

(z) decreases if the gradients decrease.

In this section we have considered the case of a discontinuous variation across

an inﬁnitely thin interface and shown that the ﬂow is always unstable. The case of

continuous variation is considered in the following section. We shall see that a certain

condition must be satisﬁed in order for the ﬂow to be unstable.

7. Instability of Continuously Stratiﬁed Parallel Flows

An instability of great geophysical importance is that of an inviscid stratiﬁed ﬂuid

in horizontal parallel ﬂow. If the density and velocity vary discontinuously across

an interface, the analysis in the preceding section shows that the ﬂow is uncondi-

tionally unstable. Although only the discontinuous case was studied by Kelvin and

Helmholtz, the more general case of continuous distribution is also commonly called

the Kelvin–Helmholtz instability.

The problem has a long history. In 1915, Taylor, on the basis of his calcula-

tions with assumed distributions of velocity and density, conjectured that a gradient

Richardson number (to be deﬁned shortly) must be less than

for instability. Other val-

ues of the critical Richardson number (ranging from 2 to

) were suggested by Prandtl,

Goldstein, Richardson, Synge, and Chandrasekhar. Finally, Miles (1961) was able to

prove Taylor’s conjecture, and Howard (1961) immediately and elegantly generalized

Miles’ proof. A short record of the history is given in Miles (1986). In this section we

shall prove the Richardson number criterion in the manner given by Howard.

Taylor–Goldstein Equation

Consider a horizontal parallel ﬂow U(z)directed along the x-axis. The z-axis is taken

vertically upwards. The basic ﬂow is in equilibrium with the undisturbed density ﬁeld

¯ρ(z)and the basic pressure ﬁeld P(z). We shall only consider two-dimensional distur-

bances on this basic state, assuming that they are more unstable than three-dimensional

disturbances; this is called Squires’ theorem and is demonstrated in Section 8 in

another context. The disturbed state has velocity, pressure, and density ﬁelds of

[U + u, 0,w],P+p, ¯ρ + ρ.

The continuity equation reduces to

∂u

∂x

∂w

∂z

= 0.

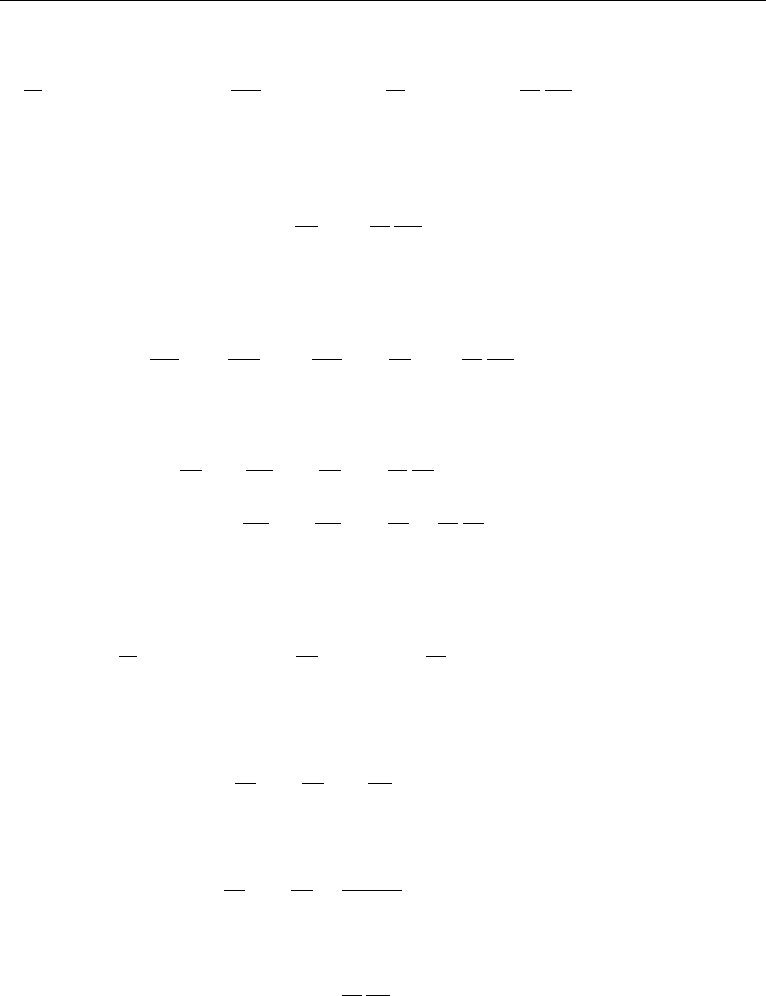
7. Instability of Continuously Stratiﬁed Parallel Flows 501

The disturbed velocity ﬁeld is assumed to satisfy the Boussinesq equation

∂

∂t

+ u

) + (U

+ u

)

∂

∂x

+ u

) =−

( ¯ρ + ρ)δ

−

∂

∂x

(P + p),

where the density variations are neglected except in the vertical equation of motion.

Here, ρ

is a reference density. The basic ﬂow satisﬁes

0 =−

g ¯ρ

−

∂P

∂x

Subtracting the last two equations and dropping nonlinear terms, we obtain the per-

turbation equation of motion

∂u

∂t

+ u

∂U

∂x

+ U

∂u

∂x

=−

gρ

−

∂p

∂x

The i = 1 and i = 3 components of the preceding equation are

∂u

∂t

+ w

∂U

∂z

+ U

∂u

∂x

=−

∂p

∂x

∂w

∂t

+ U

∂w

∂x

=−

gρ

−

∂p

∂z

(12.52)

In the absence of diffusion the density is conserved along the motion, which

requires that D(density)/Dt = 0, or that

∂

∂t

( ¯ρ + ρ) + (U + u)

∂

∂x

( ¯ρ + ρ) + w

∂

∂z

( ¯ρ + ρ) = 0.

Keeping only the linear terms, and using the fact that ¯ρ is a function of z only, we

obtain

∂ρ

∂t

+ U

∂ρ

∂x

+ w

d ¯ρ

= 0,

which can be written as

∂ρ

∂t

+ U

∂ρ

∂x

−

= 0, (12.53)

where we have deﬁned

≡−

d ¯ρ

N is the buoyancy frequency. The last term in equation (12.53) represents the density

change at a point due to the vertical advection of the basic density ﬁeld across the

point.