Cohen I.M., Kundu P.K. Fluid Mechanics
Подождите немного. Документ загружается.

332 Laminar Flow
14. Hele-Shaw Flow
Another low Reynolds number flow has seen wide application in flow visualization
apparatus because of its peculiar and surprising property of reproducing the stream-
lines of potential flows (that is, infinite Reynolds number flows).
The Hele-Shaw flow is flow about a thin object filling a narrow gap between
two parallel plates. Let the plates be located at x =±b with Re = U
o
b/ν 1.
Here, U
0
is the velocity upstream in the central plane (see Figure 9.18). Now place a
circular cylinder of radius = a and width = 2b between the plates. We will require
b/a = 1. The Hele-Shaw limit is Re
2
1. Imagine flow about a thin coin
with parallel plates bounding the ends of the coin. We are interested in the streamlines
of the flow around the cylinder. The origin of coordinates (R, θ, x) (Appendix B) is
taken at the center of the cylinder.
Consider steady flow with constant density and viscosity in the absence of body
forces. The dimensionless variables are, x
= x/b, R
= r/a, v
= v/U
o
, p
=
(p − p
∞
)/(µU
o
/b),Re= U
o
b/ν, = b/a. Conservation of mass and momentum
then take the following form (primes suppressed):
∂u
x
∂x
+
1
R
∂
∂R
(Ru
R
) +
1
R
∂u
θ
∂θ
= 0.
Re
u
x
∂u
R
∂x
+
u
R
∂u
R
∂R
+
u
θ
R
∂u
R
∂θ
−
u
2
θ
R
=−
∂p
∂R
+
∂
2
u
R
∂x
2
+
2
∂
2
u
R
∂R
2
+
1
R
∂u
R
∂R
+
1
R
2
∂
2
u
R
∂θ
2
−
u
R
R
2
−
2
R
∂u
θ
∂θ
,
Re
u
x
∂u
θ
∂x
+
u
R
∂u
θ
∂R
+
u
θ
R
∂u
θ
∂θ
−
u
R
u
θ
R
=−
1
R
∂p
∂θ
+
∂
2
u
θ
∂x
2
+
2
∂
2
u
θ
∂R
2
+
1
R
∂u
θ
∂R
+
1
R
2
∂
2
u
θ
∂θ
2
−
2
R
2
∂u
R
∂θ
−
u
θ
R
2
,
side view
x 5 2b
x 5 b
a
x
top view
R
a
θ
U
o
Figure 9.18 Hele-Shaw flow.

14. Hele-Shaw Flow 333
Re
u
x
∂u
x
∂x
+
u
R
∂u
x
∂R
+
u
θ
R
∂u
x
∂θ
=−
∂p
∂x
+
2
∂
2
u
x
∂R
2
+
1
R
∂u
x
∂R
+
1
R
2
∂
2
u
x
∂θ
2
.
Because Re
2
1, we take the limit Re → 0 first and drop the convective
acceleration. Next, we take the limit → 0 to obtain the outer region flow:
∂u
x
∂x
= O() → 0,u
x
(x =±1) = 0, so u
x
= 0 throughout,
∂
2
u
R
∂x
2
=
∂p
∂R
+ O(
2
),
∂
2
u
θ
∂x
2
=
1
R
∂p
∂θ
+ O(
2
).
With u
x
= O() at most, ∂p/∂x = O() at most so p = p(R, θ). Integrating the
momentum equations with respect to x,
u
R
=−
∂
∂R
1
2
p(1 − x
2
)
,u
θ
=−
1
R
∂
∂θ
1
2
p(1 − x
2
)
,
where no slip has been satisfied on x =±1. Thus we can write u =∇φ for the
two-dimensional field u
R
, u
θ
. Here, φ =−
1
2
p(1 − x
2
). Now we require that u
x
=
o() so that the first term in the continuity equation is small compared with the
others. Then
1
R
∂
∂R
(Ru
R
) +
1
R
∂u
θ
∂θ
= o(1) → 0as → 0
Substituting in terms of the velocity potential φ,wehave∇
2
φ = 0inR, θ subject to
the boundary conditions:
R = 1,
∂φ
∂R
= 0 (no mass flow normal to a solid boundary)
R →∞, φ → R cos θ(1 − x
2
)/2 (uniform flow in each x =
constant plane)
The solution is just the potential flow over a circular cylinder (equation (6.35))
φ = R cos θ
1 +
1
R
2
(1 − x
2
)
2
,
where x is just a parameter. Therefore, the streamlines corresponding to this velocity
potential are identical to the potential flow streamlines of equation (6.35). This allows
for the construction of an apparatus to visualize such potential flows by dye injection
between two closely spaced glass plates. The velocity distribution of this flow is
334 Laminar Flow
u
θ
=−sin θ
1 +
1
R
2
1 − x
2
2
,u
R
= cos θ
1 −
1
R
2
1 − x
2
2
.
As R → 1, u
R
→ 0 but there is a slip velocity u
θ
→−2 sin θ(1 − x
2
)/2.
As this is a viscous flow, there must exist a thin region near R = 1 where
the slip velocity u
θ
decreases rapidly to zero to satisfy u
θ
= 0onR = 1. This
thin boundary layer is very close to the body surface R = 1. Thus, u
R
≈ 0 and
∂p/∂R ≈ 0 throughout the layer. Now p =−R cos θ(1 + 1/R
2
) so for R ≈ 1,
(1/R)∂p/∂θ ≈ 2 sin θ . In the θ momentum equation, R derivatives become very
large so the dominant balance is
∂
2
u
θ
∂x
2
+
2
∂
2
u
θ
∂R
2
=
1
R
∂p
∂θ
= 2 sin θ.
It is clear from this balance that a stretching by 1/ is appropriate in the boundary
layer:
ˆ
R = (R − 1)/. In these terms
∂
2
u
θ
∂x
2
+
∂
2
u
θ
∂
ˆ
R
2
= 2 sin θ,
subject to u
θ
= 0on
ˆ
R = 0 and u
θ
→−2 sin θ(1 − x
2
)/2as
ˆ
R →∞(match with
outer region). The solution to this problem is
u
θ
(
ˆ
R, θ, x) =−(1 − x
2
) sin θ +
∞
n=0
A
n
cos(k
n
x)e
−k
n
ˆ
R
sin θ, k
n
=
n +
1
2
π,
A
n
=
1
−1
(1 − x
2
) cos
n +
1
2
πx
dx.
We conclude that Hele-Shaw flow indeed simulates potential flow (inviscid) stream-
lines except for a very thin boundary layer of the order of the plate separation adjacent
to the body surface.
15. Final Remarks
As in other fields, analytical methods in fluid flow problems are useful in understand-
ing the physics and in making generalizations. However, it is probably fair to say
that most of the analytically tractable problems in ordinary laminar flow have already
been solved, and approximate methods are now necessary for further advancing our
knowledge. One of these approximate techniques is the perturbation method, where
the flow is assumed to deviate slightly from a basic linear state; perturbation methods
are discussed in the following chapter. Another method that is playing an increas-
ingly important role is that of solving the Navier–Stokes equations numerically using
a computer. A proper application of such techniques requires considerable care and
familiarity with various iterative techniques and their limitations. It is hoped that the
reader will have the opportunity to learn numerical methods in a separate study. In
Chapter 11, we will introduce several basic methods of computational fluid dynamics.

Exercises 335
Exercises
1. Consider the laminar flow of a fluid layer falling down a plane inclined at
an angle θ with the horizontal. If h is the thickness of the layer in the fully developed
stage, show that the velocity distribution is
u =
g sin θ
2ν
(h
2
− y
2
),
where the x-axis points along the free surface, and the y-axis points toward the plane.
Show that the volume flow rate per unit width is
Q =
gh
3
sin θ
3ν
,
and the frictional stress on the wall is
τ
0
= ρgh sin θ.
2. Consider the steady laminar flow through the annular space formed by two
coaxial tubes. The flow is along the axis of the tubes and is maintained by a pressure
gradient dp/dx, where the x direction is taken along the axis of the tubes. Show that
the velocity at any radius r is
u(r) =
1
4µ
dp
dx
r
2
− a
2
−
b
2
− a
2
ln (b/a)
ln
r
a
,
where a is the radius of the inner tube and b is the radius of the outer tube. Find the
radius at which the maximum velocity is reached, the volume rate of flow, and the
stress distribution.
3. A long vertical cylinder of radius b rotates with angular velocity concen-
trically outside a smaller stationary cylinder of radius a. The annular space is filled
with fluid of viscosity µ. Show that the steady velocity distribution is
u
θ
=
r
2
− a
2
b
2
− a
2
b
2
r
.
Show that the torque exerted on either cylinder, per unit length, equals
4πµa
2
b
2
/(b
2
− a
2
).
4. Consider a solid cylinder of radius R, steadily rotating at angular speed in
an infinite viscous fluid. As shown in Section 6, the steady solution is irrotational:
u
θ
=
R
2
r
.

336 Laminar Flow
Show that the work done by the external agent in maintaining the flow (namely, the
value of 2πRu
θ
τ
rθ
at r = R) equals the total viscous dissipation rate in the flow field.
5. Suppose a line vortex of circulation is suddenly introduced into a fluid at
rest. Show that the solution is
u
θ
=
2πr
e
−r
2
/4νt
.
Sketch the velocity distribution at different times. Calculate and plot the vorticity, and
observe how it diffuses outward.
6. Consider the development from rest of a plane Couette flow. The flow is
bounded by two rigid boundaries at y = 0 and y = h, and the motion is started
from rest by suddenly accelerating the lower plate to a steady velocity U. The upper
plate is held stationary. Notice that similarity solutions cannot exist because of the
appearance of the parameter h. Show that the velocity distribution is given by
u(y, t) = U
1 −
y
h
−
2U
π
∞
n=1
1
n
exp
−n
2
π
2
νt
h
2
sin
nπy
h
.
Sketch the flow pattern at various times, and observe how the velocity reaches the
linear distribution for large times.
7. Planar Couette flow is generated by placing a viscous fluid between two infinite
parallel plates and moving one plate (say, the upper one) at a velocity U with respect
to the other one. The plates are a distance h apart. Two immiscible viscous liquids are
placed between the plates as shown in the diagram. Solve for the velocity distributions
in the two fluids.
8. Calculate the drag on a spherical droplet of radius r = a, density ρ
and
viscosity µ
moving with velocity U in an infinite fluid of density ρ and viscosity µ.
Assume Re = ρUa/µ 1. Neglect surface tension.
9. Consider a very low Reynolds number flow over a circular cyclinder of radius
r = a.Forr/a = O(1) in the Re = Ua/ν → 0 limit, find the equation governing the
streamfunction ψ(r,θ) and solve for ψ with the least singular behavior for large r.
There will be one remaining constant of integration to be determined by asymptotic
matching with the large r solution (which is not part of this problem). Find the domain
of validity of your solution.

Supplemental Reading 337
10. Consider a sphere of radius r = a rotating with angular velocity ω about a
diameter so that Re = ωa
2
/ν 1. Use the symmetries in the problem to solve the
mass and momentum equations directly for the azimuthal velocity v
ϕ
(r, θ). Then find
the shear stress and torque on the sphere.
Literature Cited
Batchelor, G. K. (1967). An Introduction to Fluid Dynamics, London: Cambridge University Press.
Lighthill, M. J. (1986). An Informal Introduction to Theoretical Fluid Mechanics, Oxford, England:
Clarendon Press.
Chester, W. and D. R. Breach (with I. Proudman) (1969). “On the flow past a sphere at low Reynolds
number.” J. Fluid Mech. 37: 751–760.
Hele-Shaw, H. S. (1898). “Investigations of the Nature of Surface Resistance of Water and of Stream Line
Motion Under Certain Experimental Conditions,” Trans. Roy. Inst. Naval Arch. 40: 21–46.
Kaplun, S. (1957). “Low Reynolds number flow past a circular cylinder.” J. Math. Mech. 6: 585–603.
Millikan, R. A. (1911). “The isolation of an ion, a precision measurement of its charge, and the correction
of Stokes’ law.” Phys. Rev. 32: 349–397.
Oseen, C. W. (1910). “
¨
Uber die Stokes’sche Formel, und ¨uber eine verwandte Aufgabe in der Hydrody-
namik.” Ark Math. Astrom. Fys. 6: No. 29.
Proudman, I. and J. R. A. Pearson (1957). “Expansions at small Reynolds numbers for the flow past a
sphere and a circular cylinder.” J. Fluid Mech. 2: 237–262.
Supplemental Reading
Schlichting, H. (1979). Boundary Layer Theory, New York: McGraw-Hill.
This page intentionally left blank

Chapter 10
Boundary Layers and
Related Topics
1. Introduction ..................... 340
2. Boundary Layer Approximation. . 340
3. Different Measures of Boundary
Layer Thickness ................. 346
The u = 0.99 U Thickness ....... 346
Displacement Thickness ......... 346
Momentum Thickness ........... 347
4. Boundary Layer on a Flat Plate with
a Sink at the Leading Edge:
Closed Form Solution .......... 348
Axisymmetric Problem........... 350
5. Boundary Layer on a Flat Plate:
Blasius Solution ................. 352
Similarity Solution–Alternative
Procedure ..................... 353
Matching with External Stream . . 355
Transverse Velocity .............. 356
Boundary Layer Thickness....... 356
Skin Friction .................... 357
Falkner–Skan Solution of the Laminar
Boundary Layer Equations .... 358
Breakdown of Laminar Solution . 360
6. von Karman Momentum Integral . 362
7. Effect of Pressure Gradient ....... 364
8. Separation ...................... 366
9. Description of Flow past a Circular
Cylinder......................... 368
Low Reynolds Numbers......... 369
von Karman Vortex Street ...... 369
High Reynolds Numbers ........ 373
10. Description of Flow past
a Sphere ....................... 375
11. Dynamics of Sports Balls ....... 376
Cricket Ball Dynamics .......... 377
Tennis Ball Dynamics ........... 379
Baseball Dynamics ............. 380
12. Two-Dimensional Jets........... 381
The Wall Jet.................... 385
13. Secondary Flows ............... 388
14. Perturbation Techniques........ 389
Order Symbols and Gauge
Functions .................... 390
Asymptotic Expansion .......... 391
Nonuniform Expansion ......... 393
15. An Example of a Regular
Perturbation Problem ........... 394
16. An Example of a Singular
Perturbation Problem ........... 396
Comparison with Exact Solution 400
Why There Cannot Be a
Boundary Layer at y = 1........ 401
17. Decay of a Laminar Shear Layer 401
Exercises ....................... 407
Literature Cited ................ 409
Supplemental Reading .......... 410
339
©2010 Elsevier Inc. All rights reserved.
DOI: 10.1016/B978-0-12-381399-2.50010-1

340 Boundary Layers and Related Topics
1. Introduction
Until the beginning of the twentieth century, analytical solutions of steady fluid flows
were generally known for two typical situations. One of these was that of parallel
viscous flows and low Reynolds number flows, in which the nonlinear advective terms
were zero and the balance of forces was that between the pressure and the viscous
forces. The second type of solution was that of inviscid flows around bodies of various
shapes, in which the balance of forces was that between the inertia and pressure forces.
Although the equations of motion are nonlinear in this case, the velocity field can
be determined by solving the linear Laplace equation. These irrotational solutions
predicted pressure forces on a streamlined body that agreed surprisingly well with
experimental data for flow of fluids of small viscosity. However, these solutions also
predicted a zero drag force and a nonzero tangential velocity at the surface, features
that did not agree with the experiments.
In 1905 Ludwig Prandtl, an engineer by profession and therefore motivated to
find realistic fields near bodies of various shapes, first hypothesized that, for small
viscosity, the viscous forces are negligible everywhere except close to the solid bound-
aries where the no-slip condition had to be satisfied. The thickness of these boundary
layers approaches zero as the viscosity goes to zero. Prandtl’s hypothesis reconciled
two rather contradictory facts. On one hand he supported the intuitive idea that the
effects of viscosity are indeed negligible in most of the flow field if ν is small. At the
same time Prandtl was able to account for drag by insisting that the no-slip condition
must be satisfied at the wall, no matter how small the viscosity. This reconciliation
was Prandtl’s aim, which he achieved brilliantly, and in such a simple way that it
now seems strange that nobody before him thought of it. Prandtl also showed how
the equations of motion within the boundary layer can be simplified. Since the time
of Prandtl, the concept of the boundary layer has been generalized, and the mathe-
matical techniques involved have been formalized, extended, and applied to various
other branches of physical science. The concept of the boundary layer is considered
one of the cornerstones in the history of fluid mechanics.
In this chapter we shall explore the boundary layer hypothesis and examine its
consequences. We shall see that the equations of motion within the boundary layer
can be simplified because of the layer’s thinness, and solutions can be obtained in
certain cases. We shall also explore approximate methods of solving the flow within a
boundary layer. Some experimental data on the drag experienced by bodies of various
shapes in high Reynolds number flows, including turbulent flows, will be examined.
For those interested in sports, the mechanics of curving sports balls will be explored.
Finally, the mathematical procedure of obtaining perturbation solutions in situations
where there is a small parameter (such as 1/Re in boundary layer flows) will be briefly
outlined.
2. Boundary Layer Approximation
In this section we shall see what simplifications of the equations of motion within the
boundary layer are possible because of the layer’s thinness. Across these layers, which
exist only in high Reynolds number flows, the velocity varies rapidly enough for the
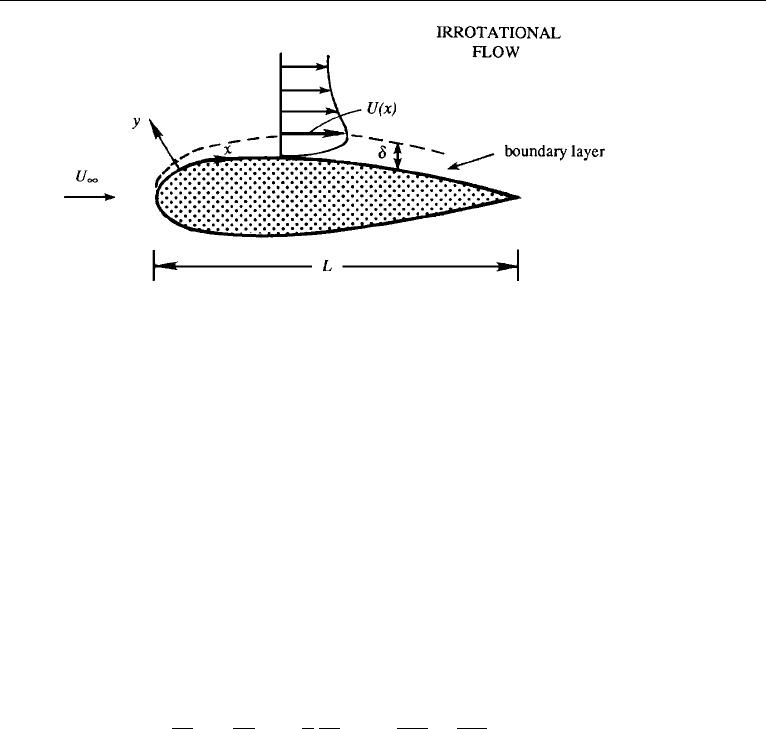
2. Boundary Layer Approximation 341
Figure 10.1 The boundary layer. Its thickness is greatly exaggerated in the figure. Here, U
∞
is the
oncoming velocity and U is the velocity at the edge of the boundary layer.
viscous forces to be important. This is shown in Figure 10.1, where the boundary
layer thickness is greatly exaggerated. (Around a typical airplane wing it is of order
of a centimeter.) Thin viscous layers exist not only next to solid walls but also in the
form of jets, wakes, and shear layers if the Reynolds number is sufficiently high. To
be specific, we shall consider the case of a boundary layer next to a wall, adopting a
curvilinear “boundary layer coordinate system” in which x is taken along the surface
and y is taken normal to it. We shall refer to the solution of the irrotational flow
outside the boundary layer as the “outer” problem and that of the boundary layer flow
as the “inner” problem.
The thickness of the boundary layer varies with x; let
¯
δ be the average thickness
of the boundary layer over the length of the body. A measure of
¯
δ can be obtained by
considering the order of magnitude of the various terms in the equations of motion.
The steady equation of motion for the longitudinal component of velocity is
u
∂u
∂x
+ v
∂u
∂y
=−
1
ρ
∂p
∂x
+ ν
∂
2
u
∂x
2
+
∂
2
u
∂y
2
. (10.1)
The Cartesian form of the conservation laws is valid only when
¯
δ/R 1, where
R is the local radius of curvature of the body shape function. The more general
curvilinear form for arbitrary R(x) is given in Goldstein (1938) and Schlichting
(1979). We generally expect
¯
δ/R to be small for large Reynolds number flows over
slender shapes. The first equation to be affected is the y-momentum equation where
centrifugal acceleration will enter the normal component of the pressure gradient.
In equation (10.1) we have also neglected body forces and any variations of ρ and
µ. The essential features of viscous boundary layers can be more clearly illustrated
without additional complications.
Let a characteristic magnitude of u in the flow field be U
∞
, which can be identified
with the upstream velocity at large distances from the body. Let L be the streamwise
distance over which u changes appreciably. The longitudinal length of the body can
serve as L, because u within the boundary layer does change by a large fraction of
U
∞
in a distance L (Figure 10.2). A measure of ∂u/∂x is therefore U
∞
/L, so that a
