Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

362 Boundary Layers and Related Topics

6. von Karman Momentum Integral

Exact solutions of the boundary layer equations are possible only in simple cases,

such as that over a ﬂat plate. In more complicated problems a frequently applied

approximate method satisﬁes only an integral of the boundary layer equations across

the layer thickness. The integral was derived by von Karman in 1921 and applied to

several situations by Pohlhausen.

The point of an integral formulation is to obtain the information that is really

required with minimum effort. The important results of boundary layer calculations

are the wall shear stress, displacement thickness, and separation point. With the help

of the von Karman momentum integral derived in what follows and additional corre-

lations, these results can be obtained easily.

The equation is derived by integrating the boundary layer equation

∂u

∂x

+ v

∂u

∂y

= U

+ ν

∂

∂y

from y = 0toy = h, where h>δis any distance outside the boundary layer. Here

the pressure gradient term has been expressed in terms of the velocity U(x) at the

edge of the boundary layer, where the inviscid Euler equation applies. Adding and

subtracting u(dU/dx), we obtain

(U − u)

+ u

∂(U − u)

∂x

+ v

∂(U − u)

∂y

=−ν

∂

∂y

. (10.42)

Integrating from y = 0toy = h, the various terms of this equation transform as

follows.

The ﬁrst term gives



(U − u)

dy = Uδ

∗

Integrating by parts, the third term gives,



∂(U − u)

∂y

dy =



v(U − u)



−



∂v

∂y

(U − u) dy



∂u

∂x

(U − u) dy,

where we have used the continuity equation and the conditions that v = 0aty = 0

and u = U at y = h. The last term in equation (10.42) gives

−ν



∂

∂y

dy =

6. von Karman Momentum Integral 363

where τ

is the wall shear stress.

The integral of equation (10.42) is therefore

Uδ

∗





∂(U − u)

∂x

+ (U − u)

∂u

∂x



dy =

. (10.43)

The integral in equation (10.43) equals



∂

∂x

[u(U − u)]dy =



u(U − u) dy =

θ),

where θ is the momentum thickness deﬁned by equation (10.17). Equation (10.43)

then gives

θ) + δ

∗

(10.44)

which is called the Karman momentum integral equation. In equation (10.44), θ,

∗

, and τ

are all unknown. Additional assumptions must be made or correlations

provided to obtain a useful solution. It is valid for both laminar and turbulent boundary

layers. In the latter case τ

cannot be equated to molecular viscosity times the velocity

gradient and should be empirically speciﬁed. The procedure of applying the integral

approach is to assume a reasonable velocity distribution, satisfying as many conditions

as possible. Equation (10.44) then predicts the boundary layer thickness and other

parameters.

The approximate method is only useful in situations where an exact solution

does not exist. For illustrative purposes, however, we shall apply it to the boundary

layer over a ﬂat plate where U(dU/dx) = 0. Using deﬁnition (10.17) for θ , equa-

tion (10.44) reduces to



(U − u)u dy =

. (10.45)

Assume a cubic proﬁle

= a + b

+ c

+ d

The four conditions that we can satisfy with this proﬁle are chosen to be

u = 0,

∂

∂y

= 0aty = 0,

u = U,

∂u

∂y

= 0aty = δ.

364 Boundary Layers and Related Topics

The condition that ∂

u/∂y

= 0 at the wall is a requirement in a boundary layer

over a ﬂat plate, for which an application of the equation of motion (10.8) gives

ν(∂

u/∂y

)

= U(dU/dx) = 0. Determination of the four constants reduces the

assumed proﬁle to





−





The terms on the left- and right-hand sides of the momentum equation (10.45)

are then



(U − u)u dy =

280

δ,

= ν



∂u

∂y



Uν

Substitution into the momentum integral equation gives

39U

280

dδ

Uν

Integrating in x and using the condition δ = 0atx = 0, we obtain

δ = 4.64



νx/U,

which is remarkably close to the exact solution (10.36). The friction factor is

(1/2)ρU

(3/2)U ν/δ

(1/2)U

0.646

√

which is also very close to the exact solution of equation (10.38).

Pohlhausen found that a fourth-degree polynomial was necessary to exhibit sen-

sitivity of the velocity proﬁle to the pressure gradient. Adding another term below

equation (10.45), e(y/δ)

requires an additional boundary condition, ∂

u/∂y

= 0

at y = δ. With the assumption of a form for the velocity proﬁle, equation (10.44)

may be reduced to an equation with one unknown, δ(x) with U(x), or the pressure

gradient speciﬁed. This equation was solved approximately by Pohlhausen in 1921.

This is described in Yih (1977, pp. 357–360). Subsequent improvements by Holstein

and Bohlen (1940) are recounted in Schlichting (1979, pp. 206–217) and Rosenhead

(1988, pp. 293–297). Sherman (1990, pp. 322–329) related the approximate solution

due to Thwaites.

7. Effect of Pressure Gradient

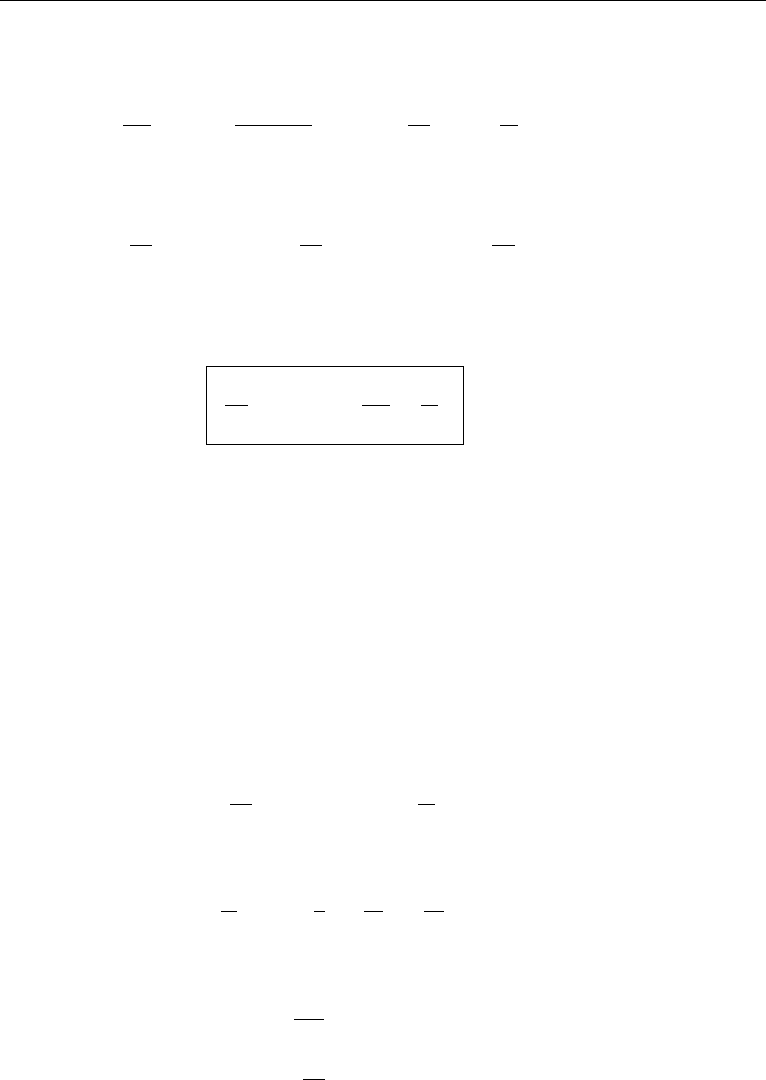
So far we have considered the boundary layer on a ﬂat plate, for which the pressure

gradient of the external stream is zero. Now suppose that the surface of the body is

curved (Figure 10.13). Upstream of the highest point the streamlines of the outer ﬂow

converge, resulting in an increase of the free stream velocity U(x) and a consequent

7. Effect of Pressure Gradient 365

Figure 10.13 Velocity proﬁles across boundary layers with favorable and adverse pressure gradients.

fall of pressure with x. Downstream of the highest point the streamlines diverge,

resulting in a decrease of U(x)and a rise in pressure. In this section we shall investigate

the effect of such a pressure gradient on the shape of the boundary layer proﬁle u(x, y).

The boundary layer equation is

∂u

∂x

+ v

∂u

∂y

=−

∂p

∂x

+ ν

∂

∂y

where the pressure gradient is found from the external velocity ﬁeld as dp/dx

=−ρU (dU/dx), with x taken along the surface of the body. At the wall, the boundary

layer equation becomes



∂

∂y



wall

∂p

∂x

In an accelerating stream dp/dx < 0, and therefore



∂

∂y



wall

< 0 (accelerating). (10.46)

As the velocity proﬁle has to blend in smoothly with the external proﬁle, the slope

∂u/∂y slightly below the edge of the boundary layer decreases with y from a positive

value to zero; therefore, ∂

u/∂y

slightly below the boundary layer edge is negative.

Equation (10.46) then shows that ∂

u/∂y

has the same sign at both the wall and the

boundary layer edge, and presumably throughout the boundary layer. In contrast, for

a decelerating external stream, the curvature of the velocity proﬁle at the wall is



∂

∂y



wall

> 0 (decelerating). (10.47)

366 Boundary Layers and Related Topics

so that the curvature changes sign somewhere within the boundary layer. In other

words, the boundary layer proﬁle in a decelerating ﬂow has a point of inﬂection

where ∂

u/∂y

= 0. In the limiting case of a ﬂat plate, the point of inﬂection is at

the wall.

The shape of the velocity proﬁles in Figure 10.13 suggests that a decelerating

pressure gradient tends to increase the thickness of the boundary layer. This can also

be seen from the continuity equation

v(y) =−



∂u

∂x

dy.

Compared to a ﬂat plate, a decelerating external stream causes a larger −∂u/∂x within

the boundary layer because the deceleration of the outer ﬂow adds to the viscous

deceleration within the boundary layer. It follows from the foregoing equation that

the v-ﬁeld, directed away from the surface, is larger for a decelerating ﬂow. The

boundary layer therefore thickens not only by viscous diffusion but also by advection

away from the surface, resulting in a rapid increase in the boundary layer thickness

with x.

If p falls along the direction of ﬂow, dp/dx < 0 and we say that the pressure

gradient is “favorable.” If, on the other hand, the pressure rises along the direction

of ﬂow, dp/dx > 0 and we say that the pressure gradient is “adverse” or “uphill.”

The rapid growth of the boundary layer thickness in a decelerating stream, and the

associated large v-ﬁeld, causes the important phenomenon of separation, in which

the external stream ceases to ﬂow nearly parallel to the boundary surface. This is

discussed in the next section.

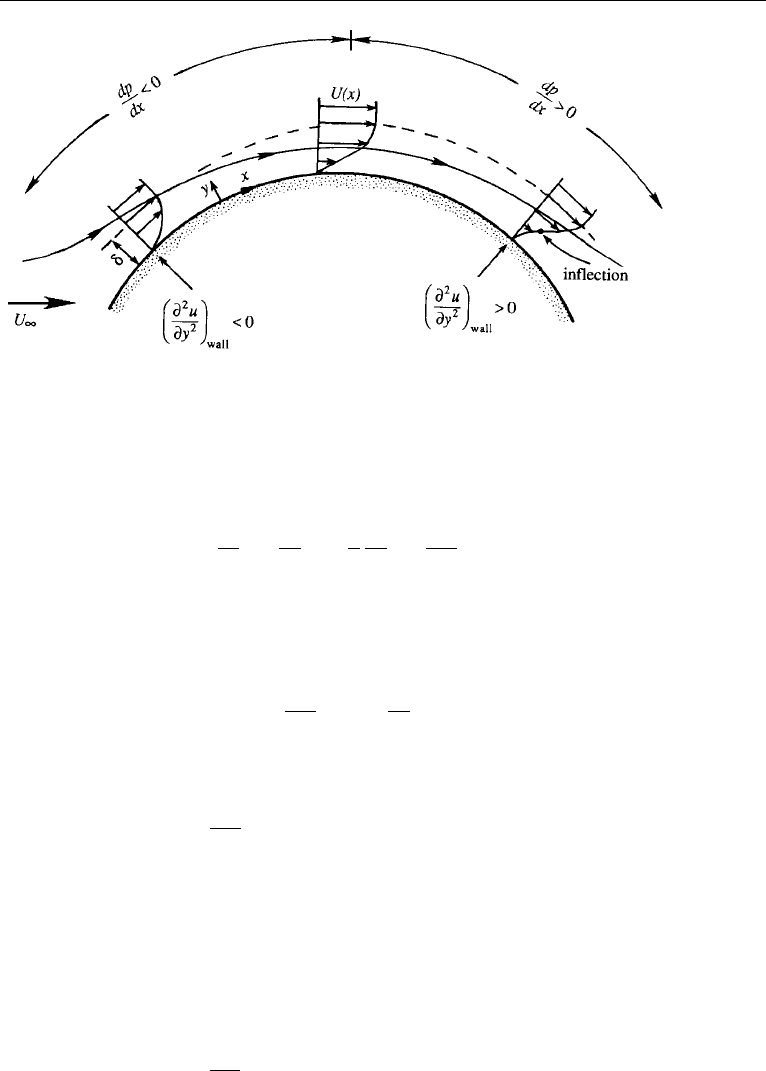
8. Separation

We have seen in the last section that the boundary layer in a decelerating stream

has a point of inﬂection and grows rapidly. The existence of the point of inﬂection

implies a slowing down of the region next to the wall, a consequence of the uphill

pressure gradient. Under a strong enough adverse pressure gradient, the ﬂow next

to the wall reverses direction, resulting in a region of backward ﬂow (Figure 10.14).

The reversed ﬂow meets the forward ﬂow at some point S at which the ﬂuid near the

surface is transported out into the mainstream. We say that the ﬂow separates from

the wall. The separation point S is deﬁned as the boundary between the forward ﬂow

and backward ﬂow of the ﬂuid near the wall, where the stress vanishes:



∂u

∂y



wall

= 0 (separation).

It is apparent from the ﬁgure that one streamline intersects the wall at a deﬁnite angle

at the point of separation.

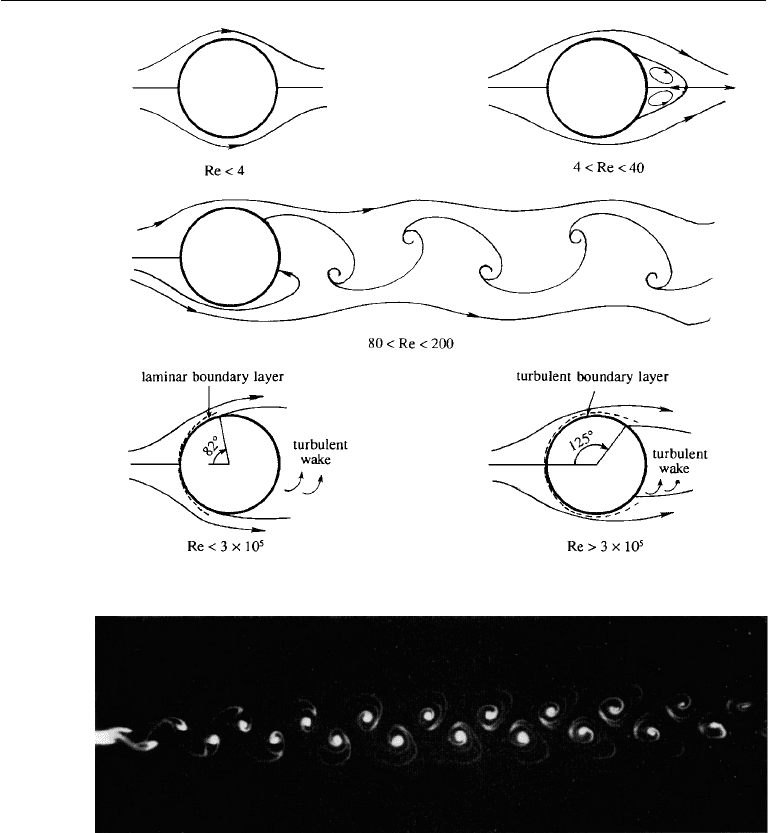
At lower Reynolds numbers the reversed ﬂow downstream of the point of sep-

aration forms part of a large steady vortex behind the surface (see Figure 10.17 in

Section 9 for the range 4 < Re < 40). At higher Reynolds numbers, when the ﬂow

8. Separation 367

Figure 10.14 Streamlines and velocity proﬁles near a separation point S. Point of inﬂection is indicated

by I. The dashed line represents u = 0.

has boundary layer characteristics, the ﬂow downstream of separation is unsteady and

frequently chaotic.

How strong an adverse pressure gradient the boundary layer can withstand with-

out undergoing separation depends on the geometry of the ﬂow, and whether the

boundary layer is laminar or turbulent. A steep pressure gradient, such as that behind

a blunt body, invariably leads to a quick separation. In contrast, the boundary layer on

the trailing surface of a thin body can overcome the weak pressure gradients involved.

Therefore, to avoid separation and large drag, the trailing section of a submerged body

should be gradually reduced in size, giving it a so-called streamlined shape.

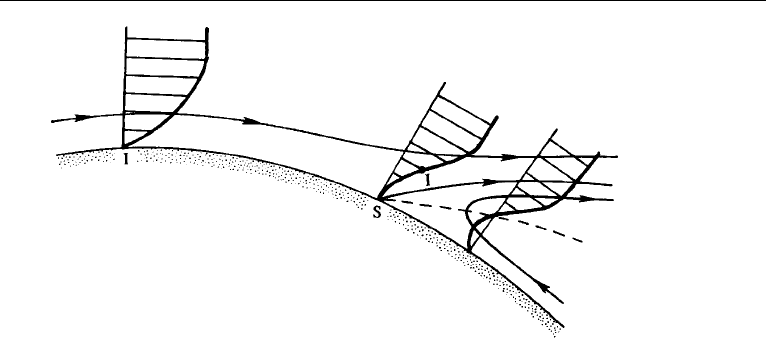
Evidence indicates that the point of separation is insensitive to the Reynolds

number as long as the boundary layer is laminar. However, a transition to turbulence

delays boundary layer separation; that is, a turbulent boundary layer is more capable

of withstanding an adverse pressure gradient. This is because the velocity proﬁle

in a turbulent boundary layer is “fuller” (Figure 10.15) and has more energy. For

example, the laminar boundary layer over a circular cylinder separates at 82

◦

from

the forward stagnation point, whereas a turbulent layer over the same body separates

at 125

◦

(shown later in Figure 10.17). Experiments show that the pressure remains

fairly uniform downstream of separation and has a lower value than the pressures on

the forward face of the body. The resulting drag due to pressure forces is called form

drag, as it depends crucially on the shape of the body. For a blunt body the form drag

is larger than the skin friction drag because of the occurrence of separation. (For a

streamlined body, skin friction is generally larger than the form drag.) As long as

the separation point is located at the same place on the body, the drag coefﬁcient

of a blunt body is nearly constant at high Reynolds numbers. However, the drag

coefﬁcient drops suddenly when the boundary layer undergoes transition to turbulence

(see Figure 10.22 in Section 9). This is because the separation point then moves

downstream, and the wake becomes narrower.

Separation takes place not only in external ﬂows, but also in internal ﬂows such as

that in a highly divergent channel (Figure 10.16). Upstream of the throat the pressure

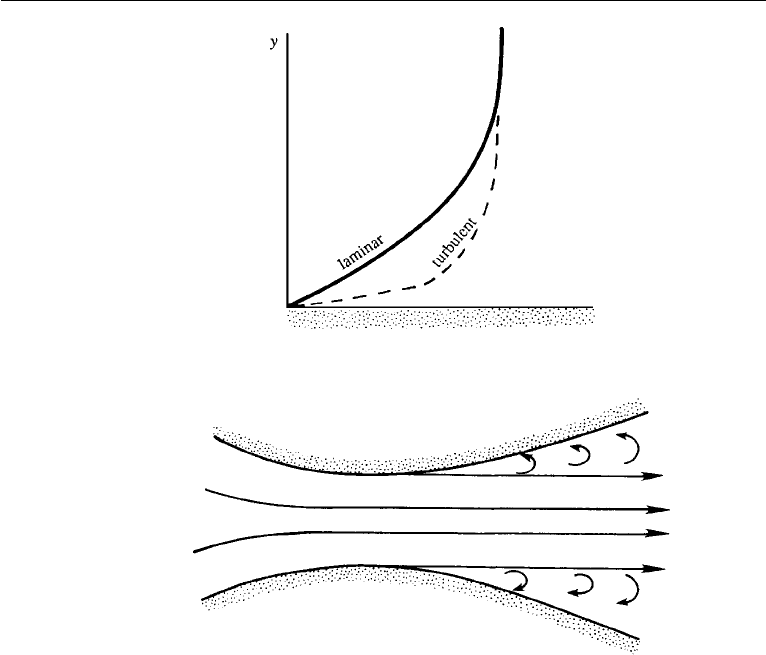
368 Boundary Layers and Related Topics

Figure 10.15 Comparison of laminar and turbulent velocity proﬁles in a boundary layer.

Figure 10.16 Separation of ﬂow in a highly divergent channel.

gradient is favorable and the ﬂow adheres to the wall. Downstream of the throat a

large enough adverse pressure gradient can cause separation.

The boundary layer equations are valid only as far downstream as the point of

separation. Beyond it the boundary layer becomes so thick that the basic underly-

ing assumptions become invalid. Moreover, the parabolic character of the boundary

layer equations requires that a numerical integration is possible only in the direc-

tion of advection (along which information is propagated), which is upstream within

the reversed ﬂow region. A forward (downstream) integration of the boundary layer

equations therefore breaks down after the separation point. Last, we can no longer

apply potential theory to ﬁnd the pressure distribution in the separated region, as the

effective boundary of the irrotational ﬂow is no longer the solid surface but some

unknown shape encompassing part of the body plus the separated region.

9. Description of Flow past a Circular Cylinder

In general, analytical solutions of viscous ﬂows can be found (possibly in terms

of perturbation series) only in two limiting cases, namely Re  1 and Re  1.

9. Description of Flow past a Circular Cylinder 369

In the Re  1 limit the inertia forces are negligible over most of the ﬂow ﬁeld; the

Stokes–Oseen solutions discussed in the preceding chapter are of this type. In the

opposite limit of Re  1, the viscous forces are negligible everywhere except close

to the surface, and a solution may be attempted by matching an irrotational outer

ﬂow with a boundary layer near the surface. In the intermediate range of Reynolds

numbers, ﬁnding analytical solutions becomes almost an impossible task, and one has

to depend on experimentation and numerical solutions. Some of these experimental

ﬂow patterns will be described in this section, taking the ﬂow over a circular cylinder

as an example. Instead of discussing only the intermediate Reynolds number range,

we shall describe the experimental data for the entire range of small to very high

Reynolds numbers.

Low Reynolds Numbers

Let us start with a consideration of the creeping ﬂow around a circular cylinder,

characterized by Re < 1. (Here we shall deﬁne Re = U

∞

d/ν, based on the upstream

velocity and the cylinder diameter.) Vorticity is generated close to the surface because

of the no-slip boundary condition. In the Stokes approximation this vorticity is simply

diffused, not advected, which results in a fore and aft symmetry. The Oseen approxi-

mation partially takes into account the advection of vorticity, and results in an asym-

metric velocity distribution far from the body (which was shown in Figure 9.17). The

vorticity distribution is qualitatively analogous to the dye distribution caused by a

source of colored ﬂuid at the position of the body. The color diffuses symmetrically

in very slow ﬂows, but at higher ﬂow speeds the dye source is conﬁned behind a

parabolic boundary with the dye source at the focus.

As Re is increased beyond 1, the Oseen approximation breaks down, and the vor-

ticity is increasingly conﬁned behind the cylinder because of advection. For Re > 4,

two small attached or “standing” eddies appear behind the cylinder. The wake is com-

pletely laminar and the vortices act like “ﬂuidynamic rollers” over which the main

stream ﬂows (Figure 10.17). The eddies get longer as Re is increased.

von Karman Vortex Street

A very interesting sequence of events begins to develop when the Reynolds number is

increased beyond 40, at which point the wake behind the cylinder becomes unstable.

Photographs show that the wake develops a slow oscillation in which the velocity

is periodic in time and downstream distance, with the amplitude of the oscillation

increasing downstream. The oscillating wake rolls up into two staggered rows of

vortices with opposite sense of rotation (Figure 10.18). von Karman investigated the

phenomenon as a problem of superposition of irrotational vortices; he concluded that

a nonstaggered row of vortices is unstable, and a staggered row is stable only if the

ratio of lateral distance between the vortices to their longitudinal distance is 0.28.

Because of the similarity of the wake with footprints in a street, the staggered row

of vortices behind a blunt body is called a von Karman vortex street. The vortices

move downstream at a speed smaller than the upstream velocity U

∞

. This means

that the vortex pattern slowly follows the cylinder if it is pulled through a stationary

ﬂuid.

370 Boundary Layers and Related Topics

Figure 10.17 Some regimes of ﬂow over a circular cylinder.

Figure 10.18 von Karman vortex street downstream of a circular cylinder at Re = 55. Flow visualized by

condensed milk. S. Taneda, Jour. Phys. Soc., Japan 20: 1714–1721, 1965, and reprinted with the permission

of The Physical Society of Japan and Dr. Sadatoshi Taneda.

In the range 40 < Re < 80, the vortex street does not interact with the pair

of attached vortices. As Re is increased beyond 80 the vortex street forms closer to

the cylinder, and the attached eddies (whose downstream length has now grown to be

about twice the diameter of the cylinder) themselves begin to oscillate. Finally the

attached eddies periodically break off alternately from the two sides of the cylinder.

While an eddy on one side is shed, that on the other side forms, resulting in an unsteady

ﬂow near the cylinder. As vortices of opposite circulations are shed off alternately

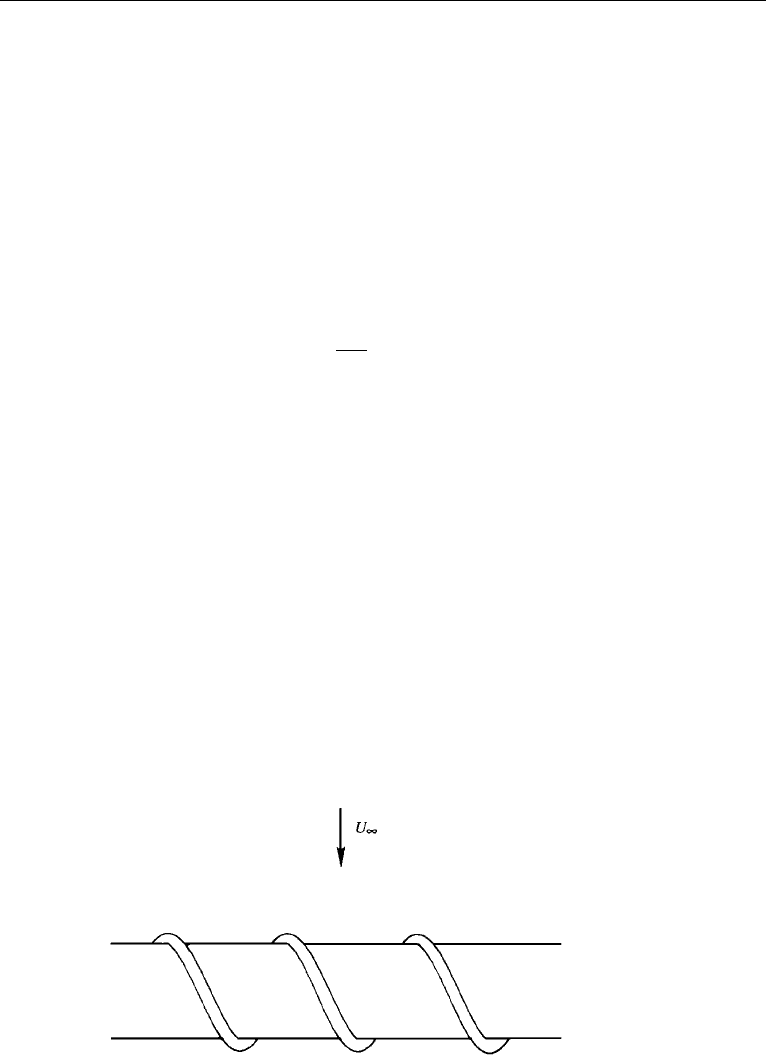
9. Description of Flow past a Circular Cylinder 371

from the two sides, the circulation around the cylinder changes sign, resulting in

an oscillating “lift” or lateral force. If the frequency of vortex shedding is close

to the natural frequency of some mode of vibration of the cylinder body, then an

appreciable lateral vibration has been observed to result. Engineering structures such

as suspension bridges and oil drilling platforms are designed so as to break up a

coherent shedding of vortices from cylindrical structures. This is done by including

spiral blades protruding out of the cylinder surface, which break up the spanwise

coherence of vortex shedding, forcing the vortices to detach at different times along

the length of these structures (Figure 10.19).

The passage of regular vortices causes velocity measurements in the wake to have

a dominant periodicity. The frequency n is expressed as a nondimensional parameter

known as the Strouhal number, deﬁned as

S ≡

∞

Experiments show that for a circular cylinder the value of S remains close to 0.21 for a

large range of Reynolds numbers. For small values of cylinder diameter and moderate

values of U

∞

, the resulting frequencies of the vortex shedding and oscillating lift lie

in the acoustic range. For example, at U

∞

= 10 m/s and a wire diameter of 2 mm,

the frequency corresponding to a Strouhal number of 0.21 is n = 1050 cycles per

second. The “singing” of telephone and transmission lines has been attributed to this

phenomenon.

Wen and Lin (2001) conducted very careful experiments that purported to be

strictly two-dimensional by using both horizontal and vertical soap ﬁlm water tun-

nels. They give a review of the recent literature on both the computational and exper-

imental aspects of this problem. The asymptote cited here of S = 0.21 is for a ﬂow

including three-dimensional instabilities. Their experiments are in agreement with

two-dimensional computations and the data are asymptotic to S = 0.2417.

Below Re = 200, the vortices in the wake are laminar and continue to be so for

very large distances downstream. Above 200, the vortex street becomes unstable and

Figure 10.19 Spiral blades used for breaking up the spanwise coherence of vortex shedding from a

cylindrical rod.