Cohen I.M., Kundu P.K. Fluid Mechanics
Подождите немного. Документ загружается.


382 Boundary Layers and Related Topics
For large Reynolds numbers, the jet is narrow and the boundary layer
approximation can be applied. Consider a control volume with sides cutting across the
jet axis at two sections (Figure 10.28); the other two sides of the control volume are
taken at large distances from the jet axis. No external pressure gradient is maintained
in the surrounding fluid, in which dp/dx is zero. According to the boundary layer
approximation, the same zero pressure gradient is also impressed upon the jet. There
is, therefore, no net force acting on the surfaces of the control volume, which requires
that the rate of flow of x-momentum at the two sections across the jet are the same.
Let u
o
(x) be the streamwise velocity on the x-axis and assume Re = u
o
x/ν is
sufficiently large for the boundary layer equations to be valid. The flow is steady,
two-dimensional (x, y), without body forces, and with constant properties (ρ,µ).
Then ∂/∂y ∂/∂x, v u, ∂p/∂y = 0, so
∂u/∂x + ∂v/∂y = 0, (10.48)
u∂u/∂x + v∂u/∂y = ν∂
2
u/∂y
2
(10.49)
subject to the boundary conditions: y →±∞:u = 0;y = 0 :v = 0;x = x
o
:
u =˜u(x
o
,y). Form u· [equation (10.48)] + equation (10.49) and integrate over all y:
∞
−∞
2u(∂u/∂x)dy +
∞
−∞
(u∂v/∂y + v∂u/∂y)dy = ν∂u/∂y|
∞
−∞
d/dx
∞
−∞
u
2
dy + uv|
∞
−∞
= ν∂u/∂y|
∞
−∞
.
Since u(y =±∞) = 0, all derivatives of u with repect to y must also be zero at
y =±∞. Then the streamwise momentum flux must be preserved,
d/dx
∞
−∞
ρu
2
dy = 0 (10.50)
Far enough downstream that (a) the boundary layer equations are valid, and (b) the
initial distribution ˜u(x
o
,y), specified at the upstream limit of validity of the boundary
layer equations, is forgotten, a similarity solution is obtained. This similarity solu-
tion is of the universal dimensionless similarity form for the laminar boundary layer
equations, that is,
ψ(x, y) =[xνu
o
(x)]
1/2
f(η),η = (y/x)[xu
o
(x)/ν]
1/2
, Re
x
= xu
o
(x)/ν
(10.51)
where ψ is the usual streamfunction, u =−k ×∇ψ, and f and η are dimensionless.
We obtain the behavior of u
o
(x) by substitution of the similarity transformation
(10.51) into the condition (10.50)

12. Two-Dimensional Jets 383
u = ∂ψ/∂y = u
o
(x)f
(η), dy = dη[νx/u
o
(x)]
1/2
ρd/dx{u
2
o
(x)[νx/u
o
(x)]
1/2
∞
−∞
f
2
(η)dη}=0.
Since the integral is a pure constant, we must have u
3/2
o
(x) · x
1/2
= C
3/2
where C
is a dimensional constant. Then u
o
= Cx
−1/3
. C is clearly related to the intensity or
momentum flux in the jet. Now, (10.51) becomes
ψ(x, y) = (νC)
1/2
· x
1/3
f(η),η = (C/ν)
1/2
· y/x
2/3
In terms of the streamfunction, (10.49) may be written
∂ψ/∂y · ∂
2
ψ/∂y∂x − ∂ψ/∂x · ∂
2
ψ/∂y
2
= ν∂
3
ψ/∂y
3
.
Evaluating the derivatives of the streamfunction and substituting into the
x-momentum equation, we obtain
3f
+ ff
+ f
2
= 0
subject to the boundary conditions
η =±∞:f
= 0;η = 0 : f = 0.
Integrating once,
3f
+ ff
= C
1
.
Evaluating at η =±∞,C
1
= 0. Integrating again,
3f
+ f
2
/2 = 18C
2
2
,
where the constant of integration is chosen to be “18C
2
2
” for convenience in the next
integration, as will be seen. Now consider the transformation f/6 = g
/g, so that
f
/6 = g
/g − g
2
/g
2
. This results in g
− C
2
2
g = 0. The solution for g is
g = C
3
exp(C
2
η) + C
4
exp(−C
2
η).
Then
f = 6g
/g = 6C
2
[C
3
exp(C
2
η) − C
4
exp(−C
2
η)]/[C
3
exp(C
2
η)
+ C
4
exp(−C
2
η)].
Now, f
= 6C
2
2
− f
2
/6 = 6C
2
2
{1 −[(C
3
e
C
2
η
− C
4
e
−C
2
η
)/(C
3
e
C
2
η
+ C
4
e
−C
2
η
)]
2
}
must be even in η. Or, use the boundary condition f(0) = 0. This requires C
3
= C
4
.
Then
f
(η) = 6C
2
2
[1 − tanh
2
(C
2
η)] and f(η)= 6C
2
tanh(C
2
η). Thus
f
(η) = 6C
2
2
sech
2
(C
2
η).

384 Boundary Layers and Related Topics
To obtain C
2
, recall u(x, y = 0) = u
o
(x)f
(0) = Cx
−1/3
· 6C
2
2
= u
o
(x) by our
definition of u
o
(x).
Thus 6C
2
2
= 1 and C
2
= 1/
√
6. Then f
(η) = sech
2
(η/
√
6) and u(x, y) =
u
o
(x) sech
2
(η/
√
6). The constant “C”inu
o
(x) = Cx
−1/3
is related to the momen-
tum flux in the jet via F =
∞
−∞
ρu
2
dy = 2ρC
3/2
ν
1/2
∞
0
sech
4
(η/
√
6)dη =
force per unit depth. Carrying out the integration, F = (4
√
6/3)ρC
3/2
ν
1/2
,so
C =[3F/(4
√
6ρν
1/2
)]
2/3
, in terms of the jet force per unit depth or momentum
flux. The mass flux in the jet is
˙m =
∞
−∞
ρudy = ρ
∞
−∞
u
o
(x)f
(η)dη ·[νx/u
o
(x)]
1/2
= (36ρ
2
νF)
1/3
x
1/3
.
This grows downstream because of entrainment in the jet. The entrainment may be
seen as inward flow (y component of velocity) from afar.
v =−∂ψ/∂x =−(νC)
1/2
x
−2/3
(f − 2ηf
)/3, so
v/u
o
=−(f − 2ηf
)/(3
Re
x
), Re
x
= xu
o
(x)/ν.
As
η →∞,v/u
o
→−
√
6/(3
Re
x
), downwards toward jet
η →−∞,v/u
o
→+
√
6/(3
Re
x
), upwards toward jet.
Thus the entrainment is an inward flow of mass from above and below.
The jet spreads as it travels downstream. Now f
(η) = sech
2
(η/
√
6).Ifη = 5
is taken as width of jet, 5/
√
6 = 2.04 and f
(2.04) = .065. Calling the transverse
extent y of the jet, δ,wehave5≈ (δ/x)(Cx
2/3
/ν)
1/2
so that δ ≈ 5
√
ν/Cx
2/3
. The
jet grows downstream x
2/3
. We can express the Reynolds numbers in terms of the
force or momentum flux in the jet, F
Re
x
= Cx
2/3
/ν =[3Fx/(4
√
6ρν
2
)]
2/3
, and
Re
δ
= u
o
δ/ν = 5 ·[3Fx/(4
√
6ρν
2
)]
1/3
.
By drawing sketches of the profiles of u, u
2
, and u
3
, the reader can verify that,
under similarity, the constraint
d
dx
∞
−∞
u
2
dy = 0,
must lead to
d
dx
∞
−∞
udy > 0,

12. Two-Dimensional Jets 385
and
d
dx
∞
−∞
u
3
dy < 0.
The laminar jet solution given here is not readily observable because the flow
easily breaks up into turbulence. The low critical Reynolds number for instability of
a jet or wake is associated with the existence of a point of inflection in the velocity
profile, as discussed in Chapter 12. Nevertheless, the laminar solution has revealed
several significant ideas (namely constancy of momentum flux and increase of mass
flux) that also apply to a turbulent jet. However, the rate of spreading of a turbulent
jet is faster, being more like δ ∝ x rather than δ ∝ x
2/3
(see Chapter 13).
The Wall Jet
An example of a two-dimensional jet that also shares some boundary layer character-
istics is the “wall jet.” The solution here is due to M. B. Glauert (1956). We consider a
fluid exiting a narrow slot with its lower boundary being a planar wall taken along the
x-axis (see Figure 10.29). Near the wall y = 0 and the flow behaves like a boundary
layer, but far from the wall it behaves like a free jet. The boundary layer analysis
shows that for large Re
x
the jet is thin (δ/x 1) so ∂p/∂y ≈ 0 across it. The
pressure is constant in the nearly stagnant outer fluid so p ≈ const. throughout the
flow. The boundary layer equations are
∂u
∂x
+
∂v
∂y
= 0, (10.52)
u
∂u
∂x
+ v
∂u
∂y
= ν
∂
2
u
∂y
2
, (10.53)
subject to the boundary conditions y = 0: u = v = 0; y →∞: u → 0. With an
initial velocity distribution forgotten sufficiently far downstream that Re
x
→∞, a
similarity solution is available. However, unlike the free jet, the momentum flux is
not constant; instead, it diminishes downstream because of the wall shear stress. To
obtain the conserved property in the wall jet, we start by integrating equation (10.53)
from y to ∞:
∞
y
u
∂u
∂x
dy +
∞
y
v
∂u
∂y
dy =−ν
∂u
∂y
.
Figure 10.29 The planar wall jet.

386 Boundary Layers and Related Topics
Multiply this by u and integrate from 0 to ∞:
∞
0
u
∂
∂x
∞
y
u
2
2
dy
dy +
∞
0
u
∞
y
v
∂u
∂y
dy
dy +
ν
2
∞
0
∂
∂y
u
2
dy = 0.
The last term integrates to 0 because of the boundary conditions at both ends. Inte-
grating the second term by parts and using equation (10.52) yields a term equal to the
first term. Then we have
∞
0
u
∂
∂x
∞
y
u
2
dy
dy −
∞
0
u
2
vdy = 0. (10.54)
Now consider
d
dx
∞
0
u
∞
y
u
2
dy
dy =
∞
0
∂u
∂x
∞
y
u
2
dy
dy
+
∞
0
u
∂
∂x
∞
y
u
2
dy
dy.
Using equation (10.52) in the first term on the right-hand side, integrating by parts,
and using equation (10.54), we finally obtain
d
dx
∞
0
u
∞
y
u
2
dy
dy = 0. (10.55)
This says that the flux of exterior momentum flux is constant downstream and is used
as the second condition to obtain the similarity exponents. Rewriting equation (10.53)
in terms of the streamfunction u = ∂ψ/∂y, v =−∂ψ/∂x, we obtain
∂ψ
∂y
∂
2
ψ
∂y ∂x
−
∂ψ
∂x
∂
2
ψ
∂y
2
= ν
∂
3
ψ
∂y
3
, (10.56)
subject to:
y = 0 : ψ =
∂ψ
∂y
= 0; y →∞:
∂ψ
∂y
→ 0. (10.57)
Let ¯u(x) be some average or characteristic speed of the wall jet. We will be
able to relate this to the mass flow rate and width of the jet at the completion of
this discussion. We can write the universal dimensionless similarity scaling for the
laminar boundary layer equations in terms of ¯u(x), via
ψ(x, y) =[νx ¯u(x)]
1/2
· f(η),η = (y/x)
Re
x
= (y/x)[x ¯u(x)/ν]
1/2
,
and expect this similarity to hold when x x
o
, where x
o
is the location where the
initial condition is specified, which we take to be the upstream extent of the validity
of the boundary layer equations. Then u(x, y) = ∂ψ/∂y =¯u(x)f
(η). Substituting
this into the conserved flux [(10.55)], we obtain
d/dx{¯u(x)
3
(νx/¯u)
∞
0
f
[
∞
y
f
2
dη]dη}=0,
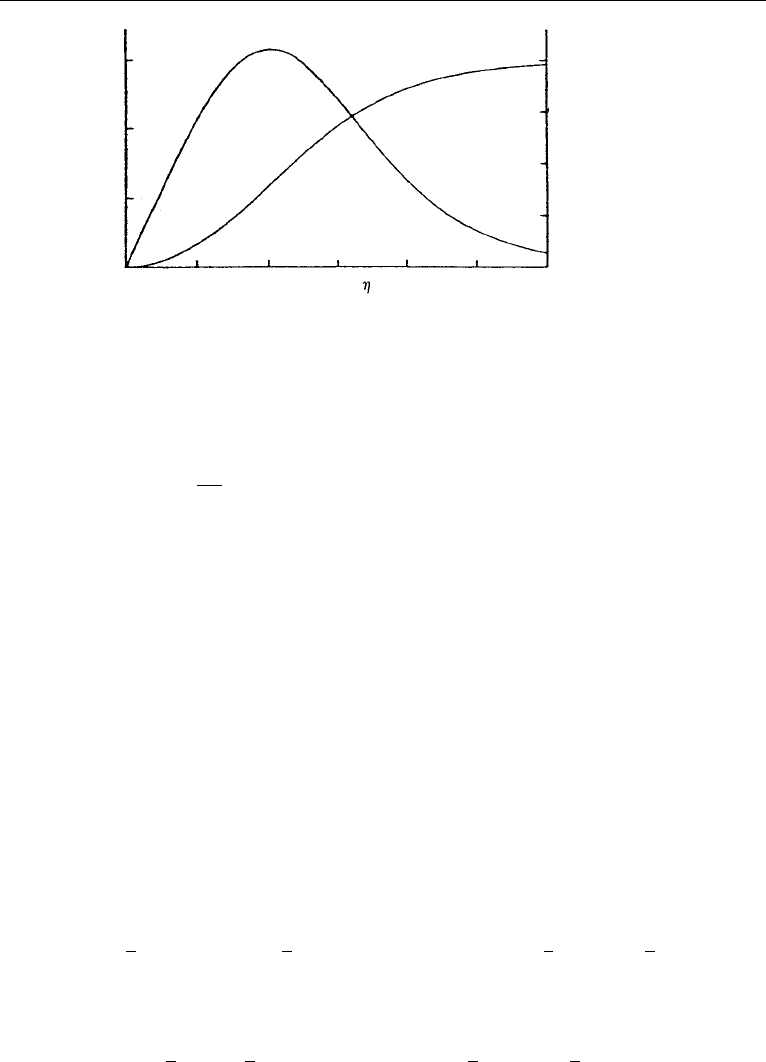
12. Two-Dimensional Jets 387
0.3
0.2
0.1
01 23456
1.0
0.75
0.5
0.25
f9
f9
f
f
Figure 10.30 Variation of normalized mass flux (f ) and normalized velocity (f
) with similarly variable
η. Reprinted with the permission of Cambridge University Press.
where we expect the integral to be independent of x. Then ( ¯u)
2
x = C
2
,or ¯u(x) =
Cx
−1/2
. This gives us the similarity transformation
ψ(x, y) =
√
νC · x
1/4
f(η), where η = (C/ν)
1/2
· y/x
3/4
.
Differentiating and substituting into (10.56), we obtain (after multiplication by
4x
2
/C
2
),
4f
+ ff
+ 2f
2
= 0
subject to the boundary conditions (10.57): f(0) = 0; f
(0) = 0; f
(∞) = 0.
This third order equation can be integrated once after multiplying by the integrating
factor f , to yield ff
− f
2
/2 + f
2
f
/4 = 0, where the constant of integration
has been evaluated at η = 0. Dividing by the integrating factor f
3/2
gives an equation
that can be integrated once more. The result is
f
−1/2
f
+ f
3/2
/6 = C
1
≡ f
3/2
∞
/6, where f
∞
= f(∞).
Since f(0) = 0, f
(0) = 0, a Tayor series for f starts with f(η) = f
(0)η
2
/2.
Then f
2
(0)/f (0) = 2f
(0) = f
3
∞
/36. Since f and η are dimensionless, f
∞
is a
pure number. The final integration can be performed after one more transformation:
f/f
∞
= g
2
( ¯η), ¯η = f
∞
η. This results in the equation dg/(1 − g
3
) = d ¯η/12. Now
1 − g
3
= (1 −g) ·(1 + g + g
2
), so integration may be effected by partial fractions,
with the result in implicit form,
−ln(1−g)+
√
3 tan
−1
[(2g +1)/
√
3]+ln(1+g +g
2
)
1/2
=¯η/4+
√
3 tan
−1
(1/
√
3),
where the boundary condition g(0) = 0 was used to evaluate the constant of inte-
gration. We can verify easily that f
→ 0 exponentially fast in η or ¯η from our
solution for g(¯η).As ¯η →∞,g → 1, so for large ¯η the solution for g reduces
to −ln(1 − g) +
√
3 tan
−1
√
3 + (1/2) ln 3
∼
=
¯η/4 +
√
3 tan
−1
(1/
√
3). The first
term on each side of the equation dominates, leaving 1 − g ≈ e
−(1/4) ¯η
.Now

388 Boundary Layers and Related Topics
f
= g(1 −g)(1 + g + g
2
)/6 ≈ (1/2)e
−(1/4) ¯η
. The mass flow rate in the jet is
˙m =
∞
0
ρudy = ρ ¯u(x)
∞
0
f
(η)dη
ν/C · x
3/4
,
or since
¯u = Cx
−1/2
, ˙m = ρ
√
νCf
∞
x
1/4
,
indicating that entrainment increases the flow rate in the jet with x
1/4
. If we define
the edge of the jet as δ(x) and say it corresponds to ¯η = 6, for example, then
δ = 6
√
ν/Cf
−1
∞
x
3/4
. If we define ¯u by requiring ˙m = ρ ¯u(x)δ(x), the two forms
for ˙m are coincident if f
2
∞
= 6. The entrainment is evident from the form of v =
−∂ψ/∂x =−
√
νC(f − 3ηf
)/(4x
3/4
) →−
√
νCf
∞
/(4x
3/4
) as η →∞,sothe
flow is downwards, toward the jet.
13. Secondary Flows
Large Reynolds number flows with curved streamlines tend to generate additional
velocity components because of properties of the boundary layer. These compo-
nents are called secondary flows and will be seen later in our discussion of insta-
bilities (p. 454). An example of such a flow is made dramatically visible by putting
finely crushed tea leaves, randomly dispersed, into a cup of water, and then stirring
vigorously in a circular motion. When the motion has ceased, all of the particles have
collected in a mound at the center of the bottom of the cup (see Figure 10.31). An
explanation of this phenomenon is given in terms of thin boundary layers. The stir-
ring motion imparts a primary velocity u
θ
(R) (see Appendix B1 for coordinates) large
enough for the Reynolds number to be large enough for the boundary layers on the
sidewalls and bottom to be thin. The largest terms in the R-momentum equation are
∂p
∂R
=
ρu
2
θ
R
.
Away from the walls, the flow is inviscid. As the boundary layer on the bottom is
thin, boundary layer theory yields ∂p/∂x = 0 from the x-momentum equation. Thus
the pressure in the bottom boundary layer is the same as for the inviscid flow just
outside the boundary layer. However, within the boundary layer, u
θ
is less than the
inviscid value at the edge. Thus p(R) is everywhere larger in the boundary layer than
that required for circular streamlines inside the boundary layer, pushing the stream-
lines inwards. That is, the pressure gradient within the boundary layer generates an
inwardly directed u
R
. This motion is fed by a downwardly directed flow in the side-
wall boundary layer and an outwardly directed flow on the top surface. This secondary
flow is closed by an upward flow along the center. The visualization is accomplished
by crushed tea leaves which are slightly denser than water. They descend by gravity
or are driven outwards by centrifugal acceleration. If they enter the sidewall boundary
layer, they are transported downwards and thence to the center by the secondary flow.
If the tea particles enter the bottom boundary layer from above, they are quickly swept

14. Perturbation Techniques 389
Figure 10.31 Secondary flow in a tea cup: (a) tea leaves randomly dispersed—initial state; (b) stirred
vigorously—transient motion; and (c) final state.
to the center and dropped as the flow turns upwards. All the particles collect at the
center of the bottom of the teacup. A practical application of this effect, illustrated in
Exercise 9, relates to sand and silt transport by the Mississippi River.
14. Perturbation Techniques
The preceding sections, based on Prandtl’s seminal idea, have revealed the physical
basis of the boundary layer concept in a high Reynolds number flow. In recent years,
the boundary layer method has become a powerful mathematical technique used to
solve a variety of other physical problems. Some elementary ideas involved in these
methods are discussed here. The interested reader should consult other specialized
texts on the subject, such as van Dyke (1975), Bender and Orszag (1978), and Nayfeh
(1981).
The essential idea is that the problem has a small parameter ε in either the
governing equation or in the boundary conditions. In a flow at high Reynolds number
the small parameter is ε = 1/Re, in a creeping flow ε = Re, and in flow around an
airfoil ε is the ratio of thickness to chord length. The solutions to these problems

390 Boundary Layers and Related Topics
can frequently be written in terms of a series involving the small parameter, the
higher-order terms acting as a perturbation on the lower-order terms. These methods
are called perturbation techniques. The perturbation expansions frequently break
down in certain regions, where the field develops boundary layers. The boundary
layers are treated differently than other regions by expressing the lateral coordinate y
in terms of the boundary layer thickness δ and defining η ≡ y/δ. The objective is to
rescale variables so that they are all finite in the thin singular region.
Order Symbols and Gauge Functions
Frequently we have a complicated function f(ε)and we want to determine the nature
of variation of f(ε)as ε → 0. The three possibilities are
f(ε) → 0 (vanishing)
f(ε) → A (bounded)
f(ε) →∞ (unbounded)
as ε → 0,
where A is finite. However, this behavior is rather vague because it does not say
how fast f(ε) goes to zero or infinity as ε → 0. To describe this behavior, we
compare the rate at which f(ε)goes to zero or infinity with the rate at which certain
familiar functions go to zero or infinity. The familiar functions used for comparison
purposes are called gauge functions. The most common example of a sequence of
gauge functions is 1,ε,ε
2
,ε
3
,.... As an example, suppose we want to find how sin ε
goes to zero as ε → 0. Using the Taylor series
sin ε = ε −
ε
3
3!
+
ε
5
5!
−···,
we find that
lim
ε→0
sin ε
ε
= lim
ε→0
1 −
ε
2
3!
+
ε
4
5!
−···
= 1,
which shows that sin ε tends to zero at the same rate at which ε tends to zero.
Another way of expressing this is to say that sin ε is of order ε as ε → 0, which we
write as
sin ε = O(ε) as ε → 0.
Other examples are that
cos ε =O(1)
cos ε − 1 = O(ε
2
)
as ε → 0.
We can generalize the concept of “order” by the following statement. A function
f(ε)is considered to be of order of a gauge function g(ε), and written
f(ε) = O[g(ε)] as ε → 0,

14. Perturbation Techniques 391
if
lim
ε→0
f(ε)
g(ε)
= A,
where A is nonzero and finite. Note that the size of the constant A is immaterial
as far as the mathematics is concerned. Thus, sin 7ε = O(ε) just as sin ε = O(ε),
and likewise 1000 = O(1). Thus, the mathematical order considered here is different
from the physical order of magnitude. However, if the physical problem has been
properly nondimensionalized, with the relevant scales judiciously chosen, then the
constant A will be of reasonable size. (Incidentally, we commonly regard a factor of
10 as a change of one physical order of magnitude, so when we say that the magnitude
of u is of order 10 cm/s, we mean that the magnitude of u is expected (or hoped!) to
be between 30 and 3 cm/s.)
Sometimes a comparison in terms of a familiar gauge function is unavailable or
inconvenient. We may say f(ε) = o[g(ε)] in the limit ε → 0if
lim
ε→0
f(ε)
g(ε)
= 0,
so that f is small compared with g as ε → 0. For example, |ln ε|=o(1/ε) in the
limit ε → 0.
Asymptotic Expansion
An asymptotic expansion of a function, in terms of a given set of gauge functions, is
essentially a series representation with a finite number of terms. Suppose the sequence
of gauge functions is g
n
(ε), such that each one is smaller than the preceding one in
the sense that
lim
ε→0
g
n+1
g
n
= 0.
Then the asymptotic expansion of f(ε)is of the form
f(ε) = a
0
+ a
1
g
1
(ε) + a
2
g
2
(ε) + O[g
3
(ε)], (10.58)
where a
n
are independent of ε. Note that the remainder, or the error, is of order of the
first neglected term. We also write
f(ε) ∼ a
0
+ a
1
g
1
(ε) + a
2
g
2
(ε),
where ∼ means “asymptotically equal to.” The asymptotic expansion of f(ε) as
ε → 0 is not unique, because a different choice of the gauge functions g
n
(ε) would
lead to a different expansion. A good choice leads to a good accuracy with only a few
terms in the expansion. The most frequently used sequence of gauge functions is the
power series ε
n
. However, in many cases the series in integral powers of ε does not
work, and other gauge functions must be used. There is a systematic way of arriving
at the sequence of gauge functions, explained in van Dyke (1975), Bender and Orszag
(1978), and Nayfeh (1981).
