Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

402 Boundary Layers and Related Topics

a detailed treatment of the decay of a laminar shear layer illustrates some interesting

points. The problem of the downstream smoothing of an initial velocity discontinuity

has not been completely solved even now, although considerable literature might

suggest otherwise. Thus it is appropriate to close this chapter with a problem that

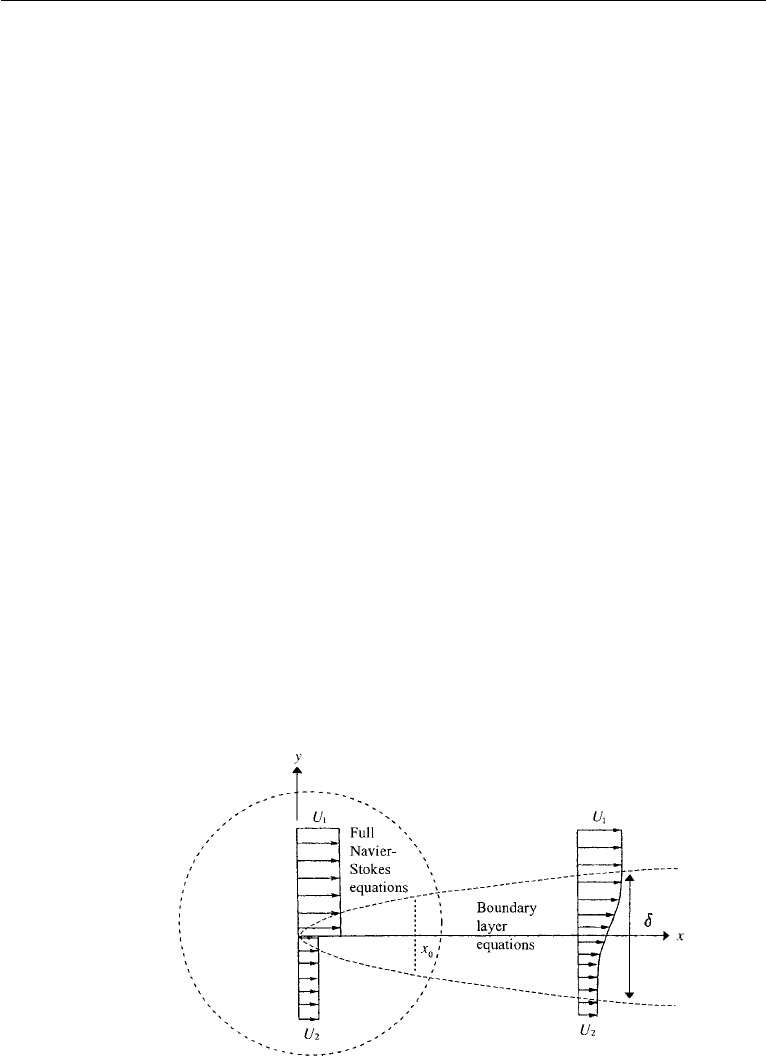
remains to be put to rest. See Figure 10.35 for a general sketch of the problem. The

basic parameter is Re

= U

x/ν. In these terms the problem splits into distinct regions

as illustrated in Figure 10.11. This shown in the paper by Alston and Cohen (1992),

which also contains a brief historical summary. In the region for which Re

is ﬁnite,

the full Navier–Stokes equations are required for a solution. As Re

becomes large,

δ  x,v  u and the Navier–Stokes equations asymptotically decay to the boundary

layer equations. The boundary layer equations require an initial condition, which is

provided by the downstream limit of the solution in the ﬁnite Reynolds number region.

Here we see that, because they are of elliptic form, the full Navier–Stokes equations

require downstream boundary conditions on u and v (which would have to be provided

by an asymptotic matching). Paradoxically it seems, the downstream limit of the

Navier–Stokes equations, represented by the boundary layer equations, cannot accept

a downstream boundary condition because they are of parabolic form. The boundary

layer equations govern the downstream evolution from a speciﬁed initial station of

the streamwise velocity proﬁle. In this problem there must be a matching between

the downstream limit of the initial ﬁnite Reynolds number region and the initial

condition for the boundary layer equations. Although the boundary layer equations

are a subset of the full Navier–Stokes equations and are generally appreciated to be the

resolution of d’Alembert’s paradox via a singular perturbation in the normal (say y)

direction, they are also a singular perturbation in the streamwise (say x) direction.

That is, the highest x derivative is dropped in the boundary layer approximation and

the boundary condition that must be dropped is the one downstream. This becomes an

issue in numerical solutions of the full Navier–Stokes equations. It arises downstream

in this problem as well.

Figure 10.35 Decay of a laminar shear layer.

17. Decay of a Laminar Shear Layer 403

If in Figure 10.35 the pressure in the top and bottom ﬂow is the same, the boundary

layer formulation valid for x>x

, Re

 1is

∂u

∂x

∂v

∂y

= 0,u

∂u

∂x

+ v

∂u

∂y

= ν

∂

∂y

y →+∞: u → U

,y→−∞: u → U

x = x

: U(x

,y) speciﬁed (initial condition). One boundary condition on v is

required.

We can look for a solution sufﬁciently far downstream that the initial condition

has been forgotten so that the similarity form has been achieved. Then,

η =



and ψ(x, y) =



νU

xf (η).

In these terms u/U

= f



(η) and





= 0,f



(∞) = 1,f



(−∞) = U

Of course a third boundary condition is required for a unique solution. This represents

the need to specify one boundary condition on v. Let us see how far we can go towards

a solution and what the missing boundary condition actually pins down. Consider the

transformation f



(η) = F(f) = u/U

. Then

dη

= F

and

dη









The Blasius equation transforms to





= 0, (10.99)

F(f =∞) = 1,F(f=−∞) = U

. (10.100)

This has a unique solution for the streamwise velocity u/U

= F in terms of the

similarity streamfunction f(η) with the expected properties, which are shown in

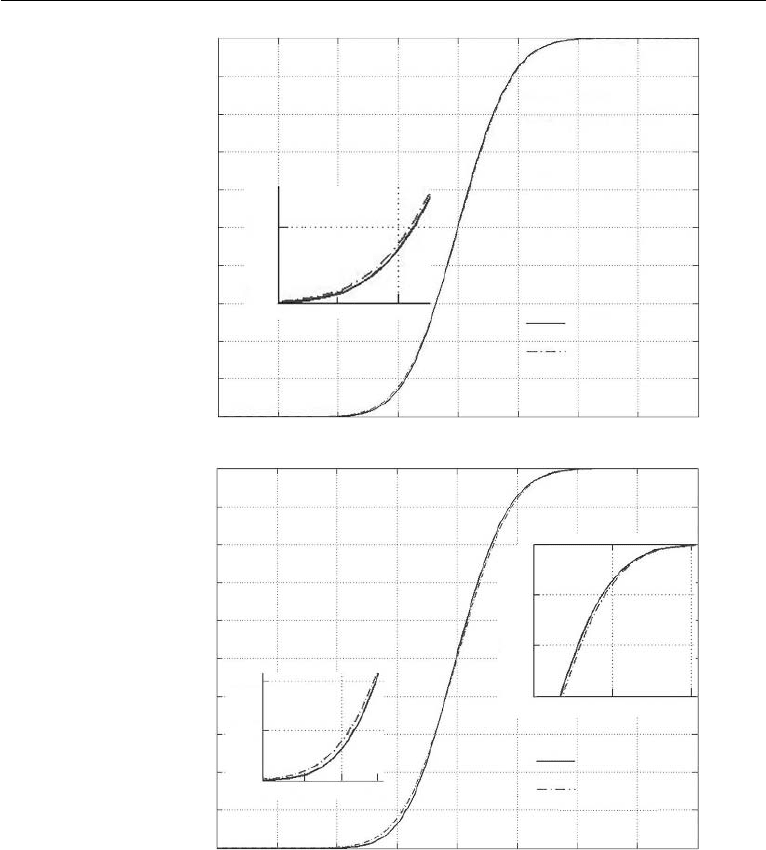
Figure 10.36(a) and (b). The exact solution varies more steeply than the linearized

solution for small velocity difference, with the greatest difference between solutions

at the region of maximum curvature at the low velocity end. This difference is shown

more clearly in the magniﬁed insets of each frame. The difference increases as the nor-

malized velocity difference, (U

−U

)/U

, increases. We can see from the (Blasius)

404 Boundary Layers and Related Topics

0.99

(a)

(b)

0.98

0.97

0.96

0.95

0.91

0.90

–3 –2

0.94

0.93

0.92

0.91

0.9

–8 –6 –4 –2 0

2468

numerical

analytical-linearized

0.98

0.96

0.92

0.88

0.86

0.84

0.82

0.8

–8 –6

–4

0.8

0.82

0.84

0.94

024

0.96

0.98

–3 –2 –1

–4 –2 0 2 4 6 8

0.9

0.94

numerical

analytical-linearized

Figure 10.36 Solution for F(f) from equation (10.99) subject to boundary conditions (10.100) when

(a) U

= 0.9, and (b) U

= 0.8. The “analytical—linearized” approximation is the asymptotic

solution for (U

− U

)/U

 1 : F = 1 −[(U

− U

)/(2U

)]erfc(f/2). Magniﬁed insets show the

difference between the two curves.

equation in η-space that the maximum of the shear stress occurs where f = 0. This

is the inﬂection point in the velocity proﬁle in η or y. However, the inﬂection point

in the F(f) curve is located where f =−2 dF/df < 0. This is below the dividing

17. Decay of a Laminar Shear Layer 405

streamline f = 0. To put this back in physical space (x, y), the transformation must

be inverted,



dη =



df/F (f ).

The integral on the right-hand side can be calculated exactly but the correspon-

dence between any integration limit on the right-hand side and that on the left-hand

side is ambiguous. This solution admits a translation of η by any constant. The ambi-

guity in the location in y (or η) of the calculated proﬁle was known to Prandtl. In the

literature, ﬁve different third boundary conditions have been used. They are as follows:

(a) f(η = 0) = 0 (v = 0ony or η = 0);

(b) f



(η = 0) = (1 +U

)/2 (average velocity on the axis);



− f → 0asη →∞(v → 0asη →∞);

(d) ηf



− f → 0asη →−∞(v → 0asη →−∞); and

(e) uv]

∞

+uv]

−∞

= 0orf



(ηf



−f)]

∞



(ηf



−f)]

−∞

= 0 (von Karman;

zero net transverse force).

Alston and Cohen (1992) considered the limit of small velocity difference (U

−U

 1 and showed that none of these third boundary conditions are correct.

As the normalized velocity difference increases, we expect the error in using any of

the incorrect boundary conditions to increase. Of all of them, the last (e) is closest

to the correct result. D.-C. Hwang, in his doctoral dissertation (2005) has shown,

that as the normalized velocity difference (U

− U

)/U

increases, the trends seen

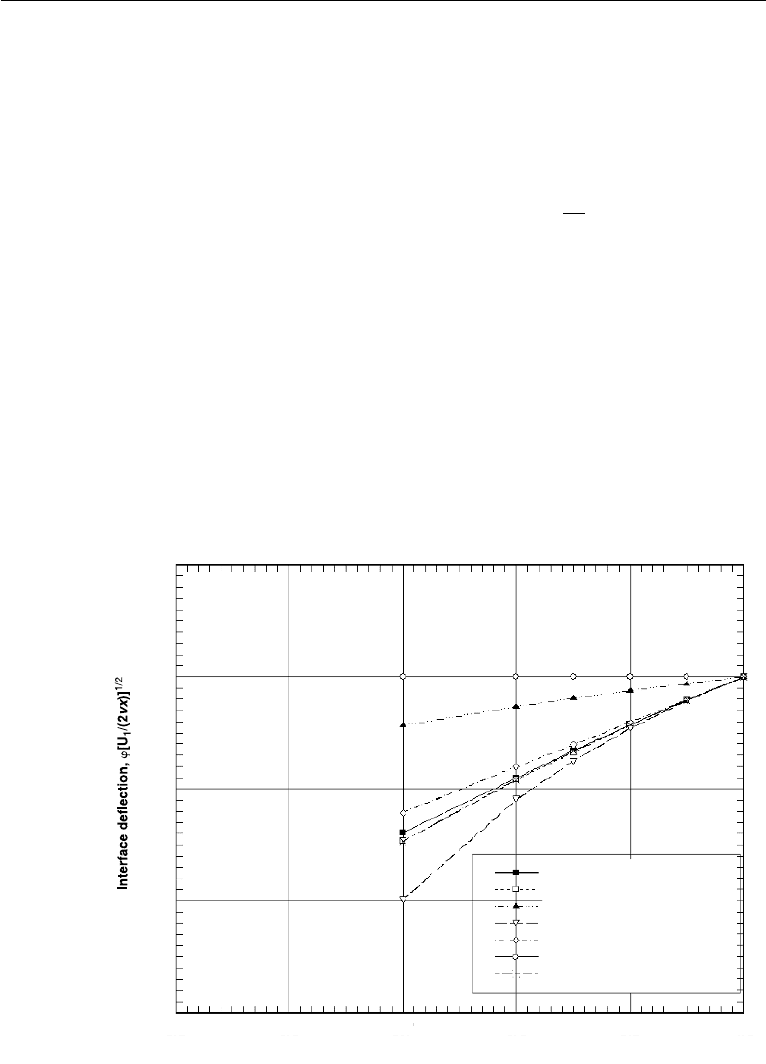
by Alston continue. Figure 10.37 shows that the streamwise velocity on the dividing

streamline (f = 0) is larger than the average velocity of the two streams, when the

upper stream is the faster one. What is not determined from the solution to (10.99)

0.5

0.55

0.6

0.65

0.7

0.75

0.8

0.85

0.9

0.95

0 0.2 0.4 0.6 0.8 1

F (f 5 0)

From solution of

Eq. (10.99) with

(10.100)

)/(2U

)

Figure 10.37 Comparison of streamwise velocity at dividing streamline (f = 0) with average velocity

(dashed line).

406 Boundary Layers and Related Topics

subject to (10.100) is the location of the dividing streamline, f = 0, because that

depends on the inverse transformation, which requires one more boundary condition

for a unique speciﬁcation. When U

, the dividing streamline ψ = 0, which

starts at the origin, bends slowly downwards and its path can be tracked only by start-

ing the solution at the origin and following the evolution of the equations downstream.

Thus, no simple statement of a third boundary condition is possible to complete the

similarity formulation. Following Klemp and Acrivos (1972), the deﬂection of the

dividing streamline from the x-axis was written by Hwang (2005) as ϕ(x). Then

a modiﬁed similarity variable η = (U

/ν)

1/2

(y − ϕ)/

√

2x was deﬁned. In these

terms, the dividing streamline is η = 0 so that the boundary condition on the dividing

streamline is f(η = 0) = 0. However, the behavior of ϕ(x) had to be computed by

solving the Navier-Stokes equations from the origin. The downstream asymptote for

ϕ(x), which can be used as the third boundary condition for the similarity solution,

is shown in Figure 10.38 as a function of velocity ratio. The downstream distance to

achieve similarity is found to be given by Re = U

x/ν ≈ 10

. Although the results

of Alston and Cohen are difﬁcult to distinguish on the graph from the von Karman

condition (e), the numerical calculation shows a clear distinction. Deviations become

larger as U

diminishes. Beyond the point shown, computations became exces-

sively tedious.

Velocity ratio, U

0.5

20.3

20.2

20.1

0.0

0.1

0.6 0.7 0.8 0.9 1.0

current solution (Hwang)

von Kármán condition

f(0) 5 Um 5 (U11U2)/2

f(0) 5 0, v(0) 5 0

Alston and Cohen

s result

v(h 5 2`) 5 0

v(h 5 `) 5 0

Figure 10.38 Asymptotic downstream dividing streamline deﬂection as a function of velocity ratio.

Exercises 407

Exercises

1. Solve the Blasius sets (10.34) and (10.35) with a computer, using the

Runge–Kutta scheme of numerical integration.

2. A ﬂat plate 4 m wide and 1 m long (in the direction of ﬂow) is immersed in

kerosene at 20

◦

C(ν = 2.29 ×10

−6

/s, ρ = 800 kg/m

) ﬂowing with an undis-

turbed velocity of 0.5 m/s. Verify that the Reynolds number is less than critical every-

where, so that the ﬂow is laminar. Show that the thickness of the boundary layer and

the shear stress at the center of the plate are δ = 0.74 cm and τ

= 0.2N/m

, and

those at the trailing edge are δ = 1.05 cm and τ

= 0.14 N/m

. Show also that the

total frictional drag on one side of the plate is 1.14 N. Assume that the similarity

solution holds for the entire plate.

3. Air at 20

◦

C and 100 kPa (ρ = 1.167 kg/m

, ν = 1.5 ×10

−5

/s) ﬂows

over a thin plate with a free-stream velocity of 6 m/s. At a point 15 cm from the

leading edge, determine the value of y at which u/U = 0.456. Also calculate v and

∂u/∂y at this point. [Answer: y = 0.857 mm, v = 0.39 cm/s, ∂u/∂y = 3020 s

−1

You may not be able to get this much accuracy, because your answer will probably

use certain ﬁgures in the chapter.]

4. Assume that the velocity in the laminar boundary layer on a ﬂat plate has the

proﬁle

= sin

πy

2δ

Using the von Karman momentum integral equation, show that

4.795

√

0.655

√

Notice that these are very similar to the Blasius solution.

5. Water ﬂows over a ﬂat plate 30 m long and 17 m wide with a free-stream veloc-

ity of 1 m/s. Verify that the Reynolds number at the end of the plate is larger than the

critical value for transition to turbulence. Using the drag coefﬁcient in Figure 10.12,

estimate the drag on the plate.

6. Find the diameter of a parachute required to provide a fall velocity no larger

than that caused by jumping from a 2.5 m height, if the total load is 80 kg. Assume

that the properties of air are ρ = 1.167 kg/m

, ν = 1.5 × 10

−5

/s, and treat the

parachute as a hemispherical shell with C

= 2.3. [Answer: 3.9 m]

7. Consider the roots of the algebraic equation

− (3 + 2ε)x + 2 +ε = 0,

for ε  1. By a perturbation expansion, show that the roots are

x =



1 − ε + 3ε

+···,

2 +3ε − 3ε

+···.

408 Boundary Layers and Related Topics

(From Nayfeh, 1981, p. 28 and reprinted by permission of John Wiley & Sons, Inc.)

8. Consider the solution of the equation

− (2x + 1)

+ 2y = 0,ε 1,

with the boundary conditions

y(0) = α, y(1) = β.

Convince yourself that a boundary layer at the left end does not generate “matchable”

expansions, and that a boundary layer at x = 1 is necessary. Show that the composite

expansion is

y = α(2x + 1) + (β − 3α)e

−3(1−x)/ε

+···.

For the two values ε = 0.1 and 0.01, sketch the solution if α = 1 and β = 0. (From

Nayfeh, 1981, p. 284 and reprinted by permission of John Wiley & Sons, Inc.)

9. Consider incompressible, slightly viscous ﬂow over a semi-inﬁnite ﬂat plate

with constant suction. The suction velocity v(x, y = 0) = v

< 0 is ordered by

O(Re

−1/2

)<v

/U < O(1) where Re = Ux/ν →∞. The ﬂow upstream is parallel

to the plate with speed U. Solve for u, v in the boundary layer.

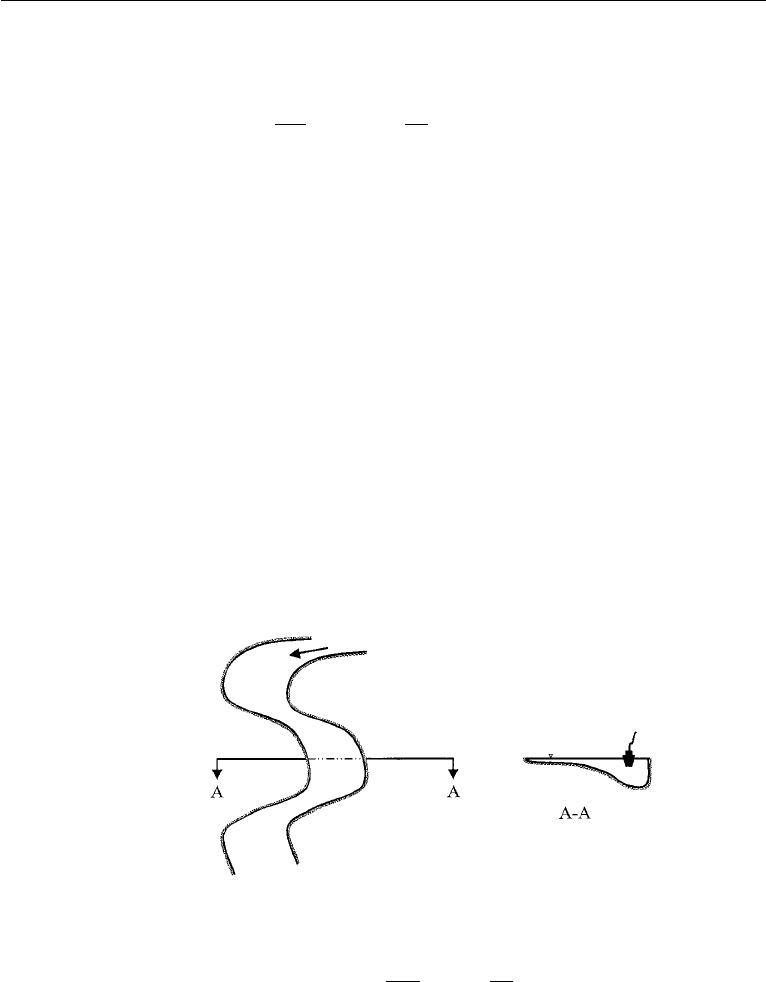
10. Mississippi River boatmen know that when rounding a bend in the river,

they must stay close to the outer bank or else they will run aground. Explain in ﬂuid

mechanical terms the reason for the cross-sectional shape of the river at the bend:

11. Solve to leading order in ε in the limit ε → 0

ε[x

−2

+ cos (ln x)]

+ cos x

+ sin xf = 0,

1  x  2,f(1) = 0,f(2) = cos 2.

12. A laminar shear layer develops immediately downstream of a velocity dis-

continuity. Imagine parallel ﬂow upstream of the origin with a velocity discontinuity

Supplemental Reading 409

at x = 0 so that u = U

for y>0 and u = U

for y<0. The density may be

assumed constant and the appropriate Reynolds number is sufﬁciently large that the

shear layer is thin (in comparison to distance from the origin). Assume the static

pressures are the same in both halves of the ﬂow at x = 0. Describe any ambiguities

or nonuniquenesses in a similarity formulation and how they may be resolved. In the

special case of small velocity difference, solve explicitly to ﬁrst order in the smallness

parameter (velocity difference normalized by average velocity, say) and show where

the nonuniqueness enters.

13. Solve equation (10.99) subject to equation (10.100) asymptotically for small

velocity difference and obtain the result in the caption to Figure 10.36.

Literature Cited

Alston, T. M. and I. M. Cohen (1992). “Decay of a laminar shear layer.” Phys. Fluids A4: 2690–2699.

Bender, C. M. and S. A. Orszag (1978). Advanced Mathematical Methods for Scientists and Engineers.

New York: McGraw-Hill.

Falkner, V. W. and S. W. Skan (1931). “Solutions of the boundary layer equations.” Phil. Mag. (Ser. 7) 12:

865–896.

Gallo, W. F., J. G. Marvin, and A. V. Gnos (1970). “Nonsimilar nature of the laminar boundary layer.”

AIAA J. 8: 75–81.

Glauert, M. B. (1956). “The Wall Jet.” J. Fluid Mech. 1: 625–643.

Goldstein, S. (ed.). (1938). Modern Developments in Fluid Dynamics, London: Oxford University Press;

Reprinted by Dover, New York (1965).

Holstein, H. and T. Bohlen (1940). “Ein einfaches Verfahren zur Berechnung laminarer Reibungsschichten

die dem N

aherungsverfahren von K. Pohlhausen gen¨ugen.” Lilienthal-Bericht. S. 10: 5–16.

Hwang, Din-Chih (2005). “Evolution of a laminar mixing layer.” Ph.D. dissertation, University of

Pennsylvania. Submitted for publication.

Klemp, J. B. and A. Acrivos (1972). “A note on the laminar mixing of two uniform parallel semi-inﬁnite

streams.” Journal of Fluid Mechanics 55: 25–30.

Mehta, R. (1985). “Aerodynamics of sports balls.” Annual Review of Fluid Mechanics 17, 151–189.

Nayfeh, A. H. (1981). Introduction to Perturbation Techniques, New York: Wiley.

Peletier, L. A. (1972). “On the asymptotic behavior of velocity proﬁles in laminar boundary layers.” Arch.

for Rat. Mech. and Anal. 45: 110–119.

Pohlhausen, K. (1921). “Zur n

aherungsweisen Integration der Differentialgleichung der laminaren

Grenzschicht.” Z. Angew. Math. Mech. 1: 252–268.

Rosenhead, L. (ed.). (1988). Laminar Boundary Layers, New York: Dover.

Schlichting, H. (1979). Boundary Layer Theory, 7th ed., New York: McGraw-Hill.

Serrin, J. (1967). “Asymptotic behaviour of velocity proﬁles in the Prandtl boundary layer theory.” Proc.

Roy. Soc. A299: 491–507.

Sherman, F. S. (1990). Viscous Flow, New York: McGraw-Hill.

Taneda, S. (1965). “Experimental investigation of vortex streets.” J. Phys. Soc. Japan 20: 1714–1721.

Thomson, R. E. and J. F. R. Gower (1977). “Vortex streets in the wake of the Aleutian Islands.” Monthly

Weather Review 105: 873–884.

Thwaites, B. (1949). “Approximate calculation of the laminar boundary layer.” Aero. Quart. 1: 245–280.

van Dyke, M. (1975). Perturbation Methods in Fluid Mechanics, Stanford, CA: The Parabolic Press.

von Karman, T. (1921). “

Uber laminare und turbulente Reibung.” Z. Angew. Math. Mech. 1: 233–252.

Wen, C.-Y. and C.-Y. Lin (2001). “Two-dimensional vortex shedding of a circular cylinder.” Phys. Fluids

13: 557–560.

Yih, C. S. (1977). Fluid Mechanics: A Concise Introduction to the Theory, Ann Arbor, MI: West River

Press.

410 Boundary Layers and Related Topics

Supplemental Reading

Batchelor, G. K. (1967). An Introduction to Fluid Dynamics, London: Cambridge University Press.

Friedrichs, K. O. (1955). “Asymptotic phenomena in mathematical physics.” Bull. Am. Math. Soc. 61:

485–504.

Lagerstrom, P. A. and R. G. Casten (1972). “Basic concepts underlying singular perturbation techniques.”

SIAM Review 14: 63–120.

Meksyn, D. (1961). New Methods in Laminar Boundary Layer Theory, New York: Pergamon Press.

Panton, R. L. (1984). Incompressible Flow, New York: Wiley.

Chapter 11

Computational Fluid Dynamics

by Howard H. Hu

University of Pennsylvania

Philadelphia, PA, USA

1. Introduction ..................... 411

2. Finite Difference Method ......... 413

Approximation to Derivatives .... 413

Discretization and Its Accuracy. . . 414

Convergence, Consistency, and

Stability ...................... 415

3. Finite Element Method ........... 418

Weak or Variational Form of Partial

Differential Equations ......... 418

Galerkin’s Approximation and

Finite Element Interpolations . . 420

Matrix Equations, Comparison

with Finite Difference Method. . 421

Element Point of View of the

Finite Element Method ........ 424

4. Incompressible Viscous Fluid Flow 426

Convection-Dominated

Problems...................... 427

Incompressibility Condition ...... 429

Explicit MacCormack Scheme.... 430

MAC Scheme .................... 433

-Scheme....................... 437

Mixed Finite Element

Formulation................... 438

5. Three Examples ................. 440

Explicit MacCormack Scheme for

Driven Cavity Flow Problem . . . 440

Explicit MacCormack Scheme for

Flow Over a Square Block ..... 444

Finite Element Formulation for

Flow Over a Cylinder Conﬁned

in a Channel .................. 450

6. Concluding Remarks ............. 461

Exercises ........................ 463

Literature Cited .................. 464

1. Introduction

Computational Fluid Dynamics (CFD) is a science that, with the help of digital com-

puters, produces quantitative predictions of ﬂuid-ﬂow phenomena based on those

conservation laws (conservation of mass, momentum, and energy) governing ﬂuid

motion. These predictions normally occur under those conditions deﬁned in terms of

ﬂow geometry, the physical properties of a ﬂuid, and the boundary and initial con-

ditions of a ﬂow ﬁeld. The prediction generally concerns sets of values of the ﬂow

variables, for example, velocity, pressure, or temperature at selected locations in the

domain and for selected times. It may also evaluate the overall behavior of the ﬂow,

such as the ﬂow rate or the hydrodynamic force acting on an object in the ﬂow.

411

DOI: 10.1016/B978-0-12-381399-2.50011-3