Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

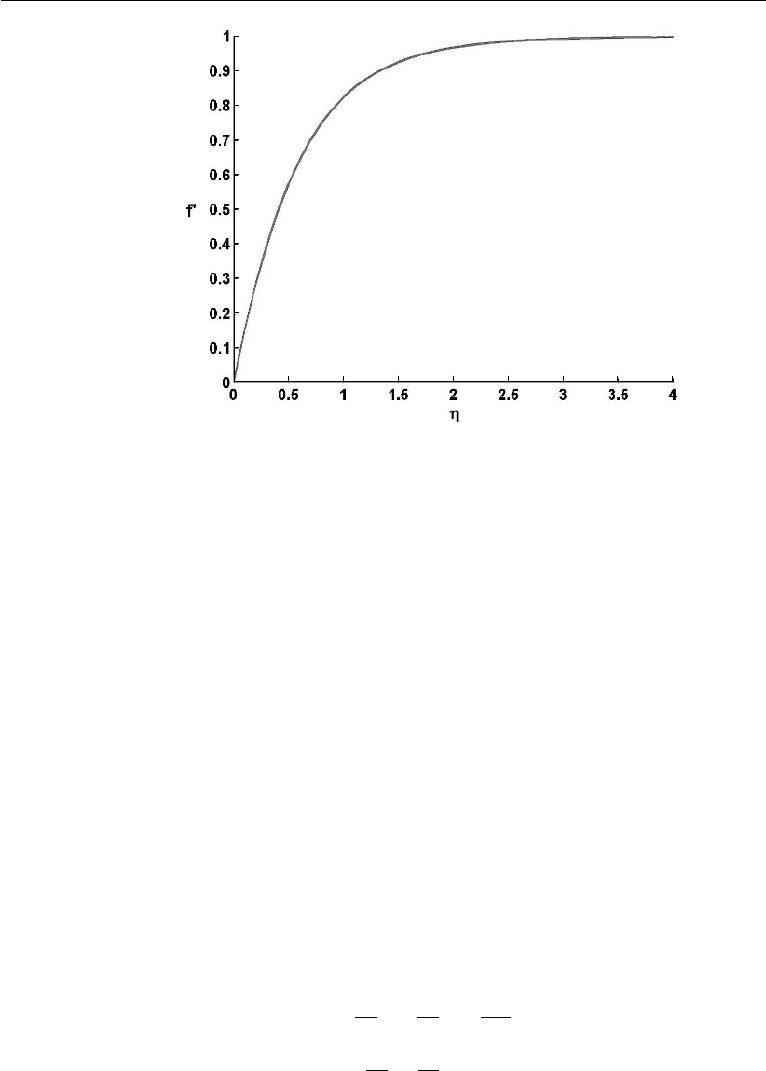
352 Boundary Layers and Related Topics

Figure 10.6 Dimensionless velocity proﬁle for ﬂow illustrated in Figure 10.5.

5. Boundary Layer on a Flat Plate: Blasius Solution

We shall next discuss the classic problem of the boundary layer on a semi-inﬁnite

ﬂat plate. Equations (10.8)–(10.10) are a valid asymptotic representation of the full

Navier–Stokes equations in the limit Re

→∞. Thus with x measured from the

leading edge, the initial station x

(see equation (10.15)) must be sufﬁciently far

downstream that U

/ν  1. A major question in boundary layer theory is the

extent of downstream memory of the initial state. If the external stream U

(x) admits

a similarity solution, is the initial condition forgotten and how soon? Serrin (1967)

and Peletier (1972) showed that for favorable pressure gradients (U

/dx) of

similarity form, the initial condition is forgotten and the larger the acceleration the

sooner similarity is achieved. A decelerating ﬂow will accentuate details of the initial

state and similarity will never be found despite its mathematical admissability. This

is consistent with the experimental ﬁndings of Gallo et al. (1970). A ﬂat plate for

which U

(x) = U = const. is the borderline case; similarity is eventually achieved

here. In the previous problem, the sink creates a rapidly accelerating ﬂow so that, if

we could ever realize such a ﬂow, similarity would be achieved quickly.

As the inviscid solution gives u = U = const. everywhere, ∂p/∂x = 0 and the

equations become

∂u

∂x

+ v

∂u

∂y

= ν

∂

∂y

∂u

∂x

∂v

∂y

= 0,

(10.19)

5. Boundary Layer on a Flat Plate: Blasius Solution 353

subject to: y = 0: u = v = 0,x>0

y → overlap at edge of boundary layer: u → U,

x = x

: u(y) given, Re

 1.

(10.20)

For x large compared with x

, we can argue that the initial condition is forgotten.

With x

no longer available for rendering the independent variables dimensionless, a

similarity solution will be obtained. Using our previous results,

ψ(x, y) =

√

νU xf (η), η =



, Re

and u = ∂ψ/∂y, v =−∂ψ/∂x.Nowu/U = f



(η) and





= 0,

f(0) = f



(0) = 0,f(∞) = 1.

A different but equally correct method of obtaining the similarity form is described in

what follows. The plate length L (Figure 10.4) has been taken very large so a solution

independent of L has been sought. In addition, we limit our consideration to a domain

far downstream of x

so the initial condition has been forgotten.

Similarity Solution—Alternative Procedure

We shall regard δ(x) as an unknown function in the following analysis; the form

of δ(x) will follow from a requirement that a similarity solution must exist for this

problem.

As there is no externally imposed length scale along x, the solutions at various

downstream locations must be self similar. Blasius, a student of Prandtl, showed

that a similarity solution can indeed be found for this problem. Clearly, the velocity

distributions at various downstream points can collapse into a single curve only if the

solution has the form

= g(η), (10.21)

where

η =

δ(x)

. (10.22)

At this point it is useful to pause a little and compare the situation with that of

a suddenly accelerated plate (see Chapter 9, Section 7), for which similarity solu-

tions exist. In that case we argued that the parameter U drops out of the equations

and boundary conditions if we deﬁne u/U as the dependent variable, leading to

u/U = f (y, t,ν). A dimensional analysis then immediately showed that the func-

tional form must be u/U = F [y/δ(t)], where δ(t) ∼

√

νt. In the current problem the

downstream distance is timelike, but we cannot analogously write u/U = f (y, x, ν),

because ν cannot be made nondimensional with the help of x or y. The dynamic

354 Boundary Layers and Related Topics

reason for this is that U cannot be eliminated from the problem simply by regarding

u/U as the dependent variable, because U still remains in the problem through the

dependence of δ on U. The correct dimensional argument in this case is that we must

have a solution of the form u/U = g[y/δ(x)], where δ(x) is a function of (U,x,ν)

and therefore can only be of the form δ ∼

√

νx/U.

We now resume our search for a similarity solution for the ﬂat plate boundary

layer. As the problem is two-dimensional, it is easier to work with the streamfunction

deﬁned by

u ≡

∂ψ

∂y

,v≡−

∂ψ

∂x

Using the similarity form (10.21), we obtain

ψ =



udy = δ



udη = δ



Ug(η) dη = Uδf(η), (10.23)

where we have deﬁned

g(η) ≡

dη

. (10.24)

(Equation (10.23) shows that the similarity form for the stream function is ψ/Uδ =

f(η), signifying that the scale for the streamfunction is proportional to the local ﬂow

rate Uδ.)

In terms of the streamfunction, the governing sets (10.19) and (10.20) become

∂ψ

∂y

∂

∂x ∂y

−

∂ψ

∂x

∂

∂y

= ν

∂

∂y

, (10.25)

subject to

∂ψ

∂y

= ψ = 0aty = 0,x>0,

∂ψ

∂y

→ U as

→∞.

(10.26)

To express sets (10.25) and (10.26) in terms of the similarity streamfunction

f(η), we ﬁnd the following derivatives from equation (10.23):

∂ψ

∂x

= U



dδ

+ δ

∂f

∂x



= U

dδ

[f − f



η], (10.27)

∂

∂x ∂y

= U

dδ

∂

∂y

[f − f



η]=−

Uηf



dδ

, (10.28)

∂ψ

∂y

= Uf



, (10.29)

5. Boundary Layer on a Flat Plate: Blasius Solution 355

∂

∂y



, (10.30)

∂

∂y



, (10.31)

where primes on f denote derivatives with respect to η. Substituting these derivatives

in equation (10.25) and canceling terms, we obtain

−



Uδ

dδ





= f



. (10.32)

In equation (10.32), f and its derivatives do not explicitly depend on x. The equation

can be valid only if

Uδ

dδ

= const.

Choosing the constant to be

for eventual algebraic simplicity, an integration gives

δ =



νx

. (10.33)

Equation (10.32) then becomes



+ f



= 0. (10.34)

In terms of f , the boundary conditions (10.26) become



(∞) = 1,

f(0) = f



(0) = 0.

(10.35)

A series solution of the nonlinear equation (10.34), subject to equation (10.35),

was given by Blasius. It is much easier to solve the problem with a computer, using for

example the Runge–Kutta technique. The resulting proﬁle of u/U = f



(η) is shown

in Figure 10.7. The solution makes the proﬁles at various downstream distances

collapse into a single curve of u/U vs y

√

U/νx, and is in excellent agreement with

experimental data for laminar ﬂows at high Reynolds numbers. The proﬁle has a

point of inﬂection (that is, zero curvature) at the wall, where ∂

u/∂y

= 0. This

is a result of the absence of pressure gradient in the ﬂow and will be discussed in

Section 7.

Matching with External Stream

We ﬁnd in this case that the difference between f



and 1 ∼ (1/η)e

−η

→ 0

exponentially fast as η →∞.

356 Boundary Layers and Related Topics

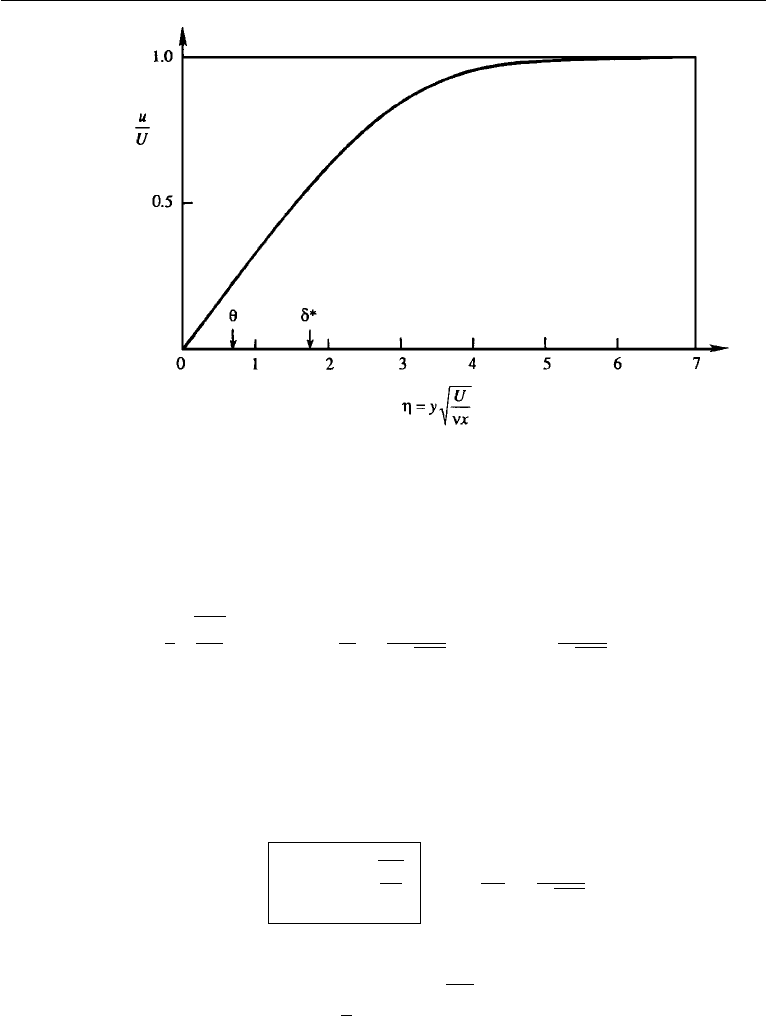
Figure 10.7 The Blasius similarity solution of velocity distribution in a laminar boundary layer on a ﬂat

plate. The momentum thickness θ and displacement δ

∗

are indicated by arrows on the horizontal axis.

Transverse Velocity

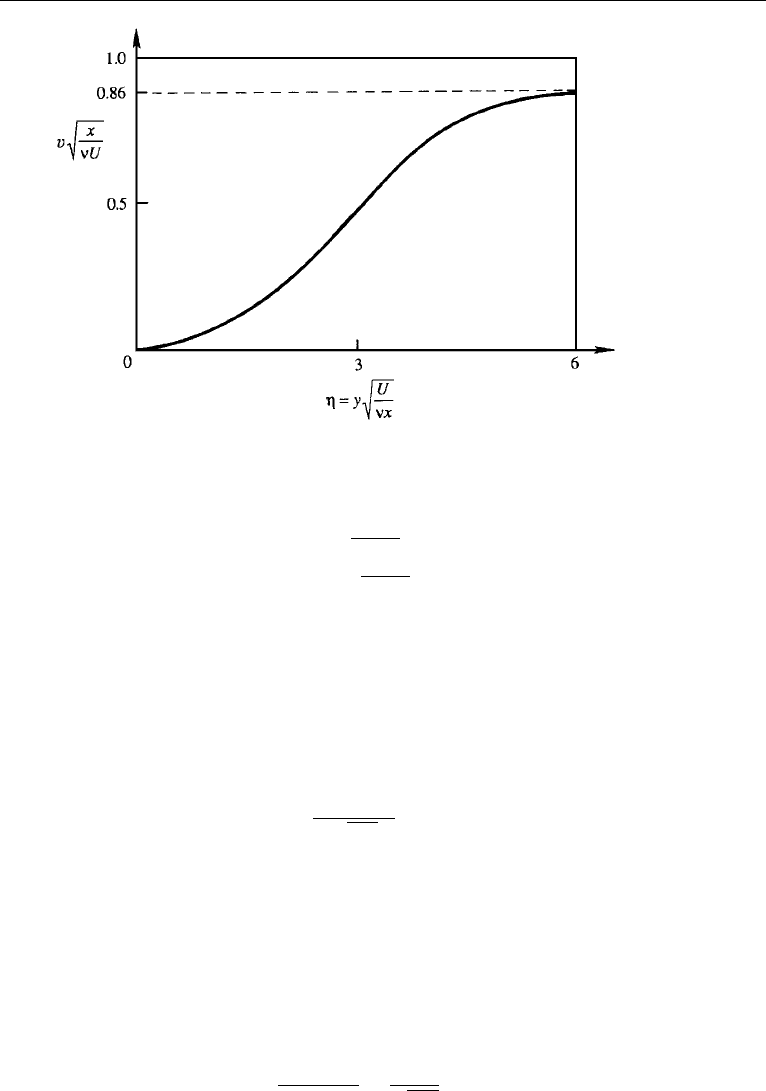
The lateral component of velocity is given by v =−∂ψ/∂x. From equation (10.27),

this becomes

v =



νU

(ηf



− f),

√

(ηf



− f) ∼

0.86

√

as η →∞,

a plot of which is shown in Figure 10.8. The transverse velocity increases from zero

at the wall to a maximum value at the edge of the boundary layer, a pattern that is in

agreement with the streamline shapes sketched in Figure 10.4.

Boundary Layer Thickness

From Figure 10.7, the distance where u = 0.99 U is η = 4.9. Therefore

= 4.9



νx

4.9

√

, (10.36)

where we have deﬁned a local Reynolds number

≡

The parabolic growth (δ ∝

√

x) of the boundary layer thickness is in good agree-

ment with experiments. For air at ordinary temperatures ﬂowing at U = 1m/s, the

Reynolds number at a distance of 1 m from the leading edge is Re

= 6 × 10

, and

equation (10.36) gives δ

= 2 cm, showing that the boundary layer is indeed thin.

5. Boundary Layer on a Flat Plate: Blasius Solution 357

Figure 10.8 Transverse velocity component in a laminar boundary layer on a ﬂat plate.

The displacement and momentum thicknesses, deﬁned in equations (10.16) and

(10.17), are found to be

∗

= 1.72



νx/U,

θ = 0.664



νx/U.

These thicknesses are indicated along the abscissa of Figure 10.7.

Skin Friction

The local wall shear stress is τ

= µ(∂u/∂y)

= µ(∂

ψ/∂y

)

, where the subscript

zero stands for y = 0. Using ∂

ψ/∂y

= Uf



/δ given in equation (10.30), we obtain

= µUf



(0)/δ, and ﬁnally

0.332ρU

√

. (10.37)

The wall shear stress therefore decreases as x

−1/2

, a result of the thickening of the

boundary layer and the associated decrease of the velocity gradient. Note that the

wall shear stress at the leading edge is predicted to be inﬁnite. Clearly the boundary

layer theory breaks down near the leading edge where the assumption ∂/∂x  ∂/∂y

is invalid. The local Reynolds number Re

in the neighborhood of the leading edge

is of order 1, for which the boundary layer assumptions are not valid.

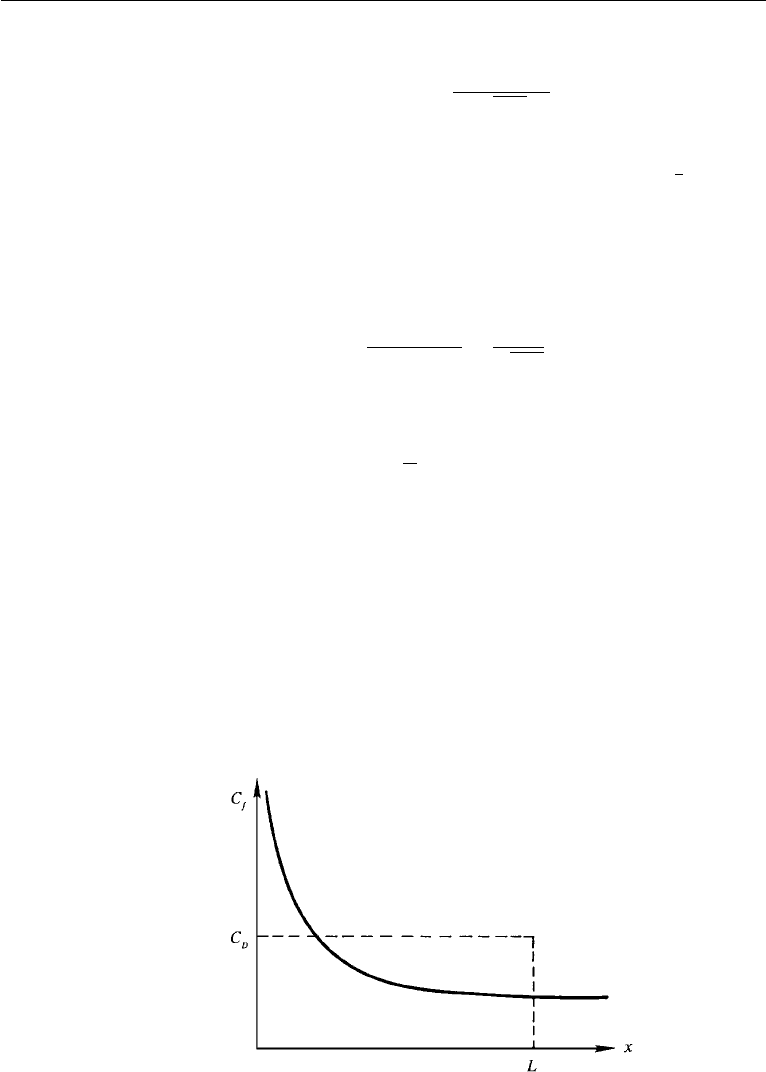
The wall shear stress is generally expressed in terms of the nondimensional skin

friction coefﬁcient

≡

(1/2)ρU

0.664

√

. (10.38)

358 Boundary Layers and Related Topics

The drag force per unit width on one side of a plate of length L is

D =



dx =

0.664ρU

√

where we have deﬁned Re

≡ U L/ν as the Reynolds number based on the plate

length. This equation shows that the drag force is proportional to the

power of

velocity. This should be compared with small Reynolds number ﬂows, where the

drag is proportional to the ﬁrst power of velocity. We shall see later in the chapter

that the drag on a blunt body in a high Reynolds number ﬂow is proportional to the

square of velocity.

The overall drag coefﬁcient deﬁned in the usual manner is

≡

(1/2)ρU

1.33

√

. (10.39)

It is clear from equations (10.38) and (10.39) that



dx,

which says that the overall drag coefﬁcient is the average of the local friction coefﬁ-

cient (Figure 10.9).

We must keep in mind that carrying out an integration from x = 0isof

questionable validity because the equations and solutions are valid only for very

large Re

Falkner–Skan Solution of the Laminar Boundary Layer Equations

No discussion of laminar boundary layer similarity solutions would be complete

without mention of the work of V. W. Falkner and S. W. Skan (1931). They found

Figure 10.9 Friction coefﬁcient and drag coefﬁcient in a laminar boundary layer on a ﬂat plate.

5. Boundary Layer on a Flat Plate: Blasius Solution 359

that U

(x) = ax

admits a similarity solution, as follows. We assume that Re

(n+1)

/ν is sufﬁciently large so that the boundary layer equations are valid and any

dependence on an initial condition has been forgotten. Then the initial station x

disappears from the problem and we may write

ψ(x, y) =



νU

(x) · x f (η) =

√

νa x

(n+1)/2

f(η),

η =





(n−1)/2

Then u/U

= f



(η) and U

(dU

/dx) = na

2n−1

The x-momentum equation reduces to the similarity form



n + 1



− nf

2

+ n = 0, (10.40)

f(0) = 0,f



(0) = 0,f



(∞) = 1. (10.41)

The Blasius equation (10.34) and (10.35) is a special case for n = 0, that is,

(x) = U . Although there are similarity solutions possible for n<0, these are not

likely to be seen in practice. For n  0, all solutions of equations (10.40) and (10.41)

have the proper behavior as detailed in the preceding. The numerical coefﬁcients

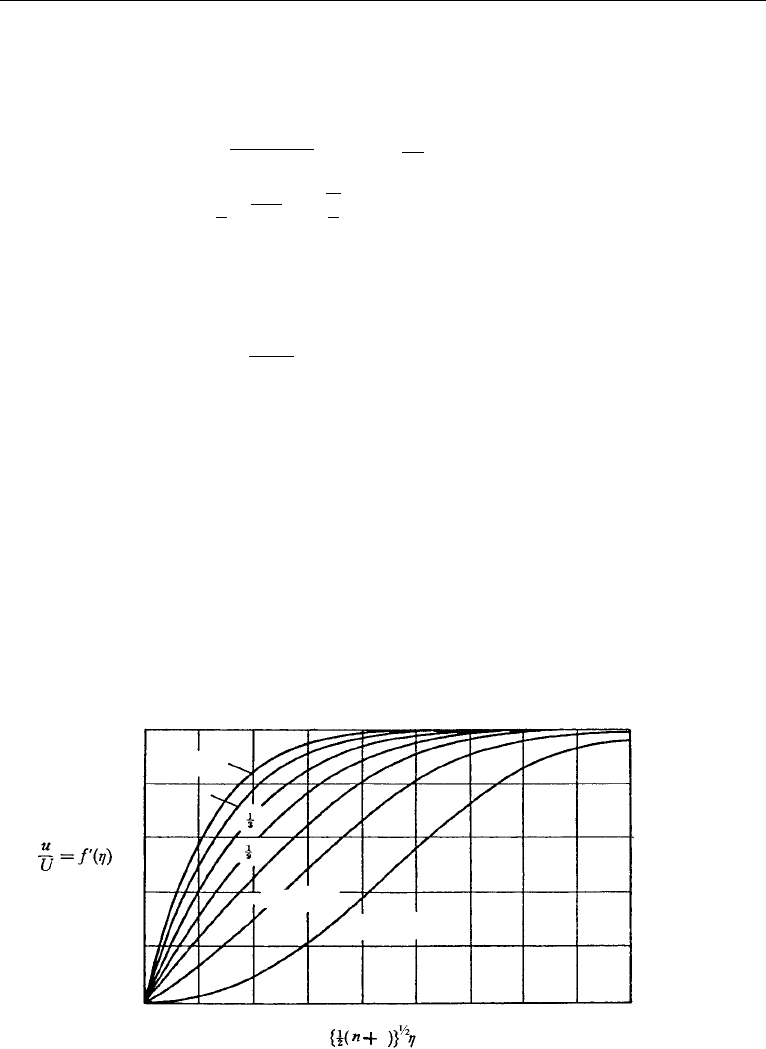
depend on n. Solutions to equations (10.40) and (10.41) are displayed in Figure 5.9.1

of Batchelor (1967) and reproduced here in Figure 10.10. They show a monotonically

increasing shear stress [f



(0)]asn increases. For n =−0.0904,f



(0) = 0soτ

= 0

and separation is imminent all along the surface. Solutions for n<−0.0904 do not

represent boundary layers. In most real ﬂows, similarity solutions are not available

and the boundary layer equations with boundary and initial conditions as written in

1.0

0.8

0.6

0.4

0.2

234

– 0.0904

– 0.0654

n =4

Figure 10.10 Velocity distribution in the boundary layer for external stream U

= ax

. G. K Batchelor,

An Introduction to Fluid Dynamics, 1st ed. (1967), reprinted with the permission of Cambridge University

Press.

360 Boundary Layers and Related Topics

equations (10.8)–(10.15) must be solved. A simple approximate procedure, the von

Karman momentum integral, is discussed in the next section. More often the equa-

tions will be integrated numerically by procedures that are discussed in more detail in

Chapter 11.

Breakdown of Laminar Solution

Agreement of the Blasius solution with experimental data breaks down at large down-

stream distances where the local Reynolds number Re

is larger than some critical

value, say Re

. At these Reynolds numbers the laminar ﬂow becomes unstable and

a transition to turbulence takes place. The critical Reynolds number varies greatly

with the surface roughness, the intensity of existing ﬂuctuations (that is, the degree

of steadiness) within the outer irrotational ﬂow, and the shape of the leading edge.

For example, the critical Reynolds number becomes lower if either the roughness of

the wall surface or the intensity of ﬂuctuations in the free stream is increased. Within

a factor of 5, the critical Reynolds number for a boundary layer over a ﬂat plate is

found to be

∼ 10

(ﬂat plate).

Figure 10.11 schematically depicts the ﬂow regimes on a semi-inﬁnite ﬂat plate. For

ﬁnite Re

= Ux/ν ∼ 1, the full Navier–Stokes equations are required to describe the

leading edge region properly. As Re

gets large at the downstream limit of the leading

edge region, we can locate x

as the maximal upstream extent of the boundary layer

Figure 10.11 Schematic depiction of ﬂow over a semiinﬁnite ﬂat plate.

5. Boundary Layer on a Flat Plate: Blasius Solution 361

equations. For some distance x>x

, the initial condition is remembered. Finally,

the inﬂuence of the initial condition may be neglected and the solution becomes of

similarity form. For somewhat larger Re

, a bit farther downstream, the ﬁrst instability

appears. Then a band of waves becomes ampliﬁed and interacts nonlinearly through

the advective acceleration. As Re

increases, the ﬂow becomes increasingly chaotic

and irregular in the downstream direction. For lack of a better word, this is called

transition. Eventually, the boundary layer becomes fully turbulent with a signiﬁcant

increase in shear stress at the plate τ

After undergoing transition, the boundary layer thickness grows faster than x

1/2

(Figure 10.11), and the wall shear stress increases faster with U than in a laminar

boundary layer; in contrast, the wall shear stress for a laminar boundary layer varies

as τ

∝ U

1.5

. The increase in resistance is due to the greater macroscopic mixing in

a turbulent ﬂow.

Figure 10.12 sketches the nature of the observed variation of the drag coef-

ﬁcient in a ﬂow over a ﬂat plate, as a function of the Reynolds number. The

lower curve applies if the boundary layer is laminar over the entire length of

the plate, and the upper curve applies if the boundary layer is turbulent over the

entire length. The curve joining the two applies if the boundary layer is laminar

over the initial part and turbulent over the remaining part, as in Figure 10.11. The

exact point at which the observed drag deviates from the wholly laminar behavior

depends on experimental conditions and the transition shown in Figure 10.12 is at

= 5 ×10

Figure 10.12 Measured drag coefﬁcient for a boundary layer over a ﬂat plate. The continuous line shows

the drag coefﬁcient for a plate on which the ﬂow is partly laminar and partly turbulent, with the transition

taking place at a position where the local Reynolds number is 5 ×10

. The dashed lines show the behavior

if the boundary layer was either completely laminar or completely turbulent over the entire length of the

plate.