Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

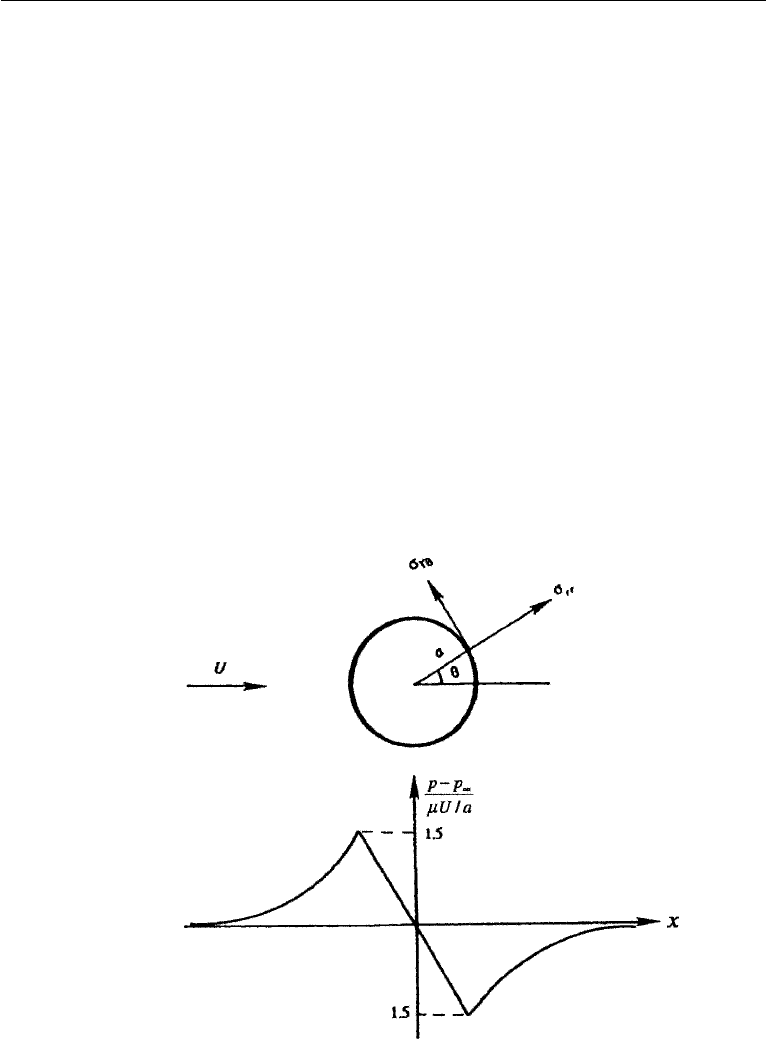
322 Laminar Flow

The proper scales depend on the nature of the ﬂow and are obtained by equating

the terms that are most important in the ﬂow ﬁeld. For a high Reynolds number

ﬂow, the dominant terms are the inertia and pressure forces. This suggests the scaling

(9.59), resulting in the nondimensional equation (9.60) in which the small parameter

multiplies the subdominant term (except in boundary layers). In contrast, the dominant

terms for a low Reynolds number ﬂow are the pressure and viscous forces. This

suggests the scaling (9.61), resulting in the nondimensional equation (9.62) in which

the small parameter multiplies the subdominant term.

12. Creeping Flow around a Sphere

A solution for the creeping ﬂow around a sphere was ﬁrst given by Stokes in 1851.

Consider the low Reynolds number ﬂow around a sphere of radius a placed in a uni-

form stream U (Figure 9.14). The problem is axisymmetric, that is, the ﬂow patterns

are identical in all planes parallel to U and passing through the center of the sphere.

Since Re → 0, as a ﬁrst approximation we may neglect the inertia forces altogether

and solve the equation

∇p = µ∇

∗

Figure 9.14 Creeping ﬂow over a sphere. The upper panel shows the viscous stress components at the

surface. The lower panel shows the pressure distribution in an axial (ϕ = const.) plane.

12. Creeping Flow around a Sphere 323

We can form a vorticity equation by taking the curl of the preceding equation,

obtaining

0 =∇

∗

Here, we have used the fact that the curl of a gradient is zero, and that the order of the

operators curl and ∇

can be interchanged. (The reader may verify this using indicial

notation.) The only component of vorticity in this axisymmetric problem is ω

, the

component perpendicular to ϕ = const. planes in Figure 9.14, and is given by



∂(ru

)

∂r

−

∂u

∂θ



In axisymmetric ﬂows we can deﬁne a streamfunction ψ given in Section 6.18. In

spherical coordinates, it is deﬁned as u =−∇ϕ × ∇ψ, (6.74) so

≡

sin θ

∂ψ

∂θ

≡−

r sin θ

∂ψ

∂r

In terms of the streamfunction, the vorticity becomes

=−



sin θ

∂

∂r

∂

∂θ



sin θ

∂ψ

∂θ



The governing equation is

∇

= 0

∗

Combining the last two equations, we obtain



∂

∂r

sin θ

∂

∂θ



sin θ

∂

∂θ



ψ = 0. (9.64)

The boundary conditions on the preceding equation are

ψ(a,θ) = 0 [u

= 0 at surface], (9.65)

∂ψ/∂r(a,θ) = 0 [u

= 0 at surface], (9.66)

ψ(∞,θ) =

sin

θ [uniform ﬂow at ∞]. (9.67)

The last condition follows from the fact that the stream function for a uniform ﬂow

is (1/2)U r

sin

θ in spherical coordinates (see equation (6.76)).

* In spherical polar coordinates, the operator in the footnoted equations is actually −∇ × ∇ ×

(−curl curl

), which is different from the Laplace operator deﬁned in Appendix B. Eq. (9.64) is the

square of the operator, and not the biharmonic.

324 Laminar Flow

The upstream condition (9.67) suggests a separable solution of the form

ψ = f(r)sin

θ.

Substitution of this into the governing equation (9.64) gives

−





−

= 0,

whose solution is

f = Ar

+ Br

+ Cr +

The upstream boundary condition (9.67) requires that A = 0 and B = U/2. The

surface boundary conditions then give C =−3 Ua/4 and D = Ua

/4. The solution

then reduces to

ψ = Ur

sin



−



. (9.68)

The velocity components can then be found as

sin θ

∂ψ

∂θ

= U cos θ



1 −



=−

r sin θ

∂ψ

∂r

=−U sin θ



1 −

−



(9.69)

The pressure can be found by integrating the momentum equation ∇p = µ∇

u. The

result is

p =−

3aµU cos θ

+ p

∞

(9.70)

The pressure distribution is sketched in Figure 9.14. The pressure is maximum at

the forward stagnation point where it equals 3µU/2a, and it is minimum at the rear

stagnation point where it equals −3µU/2a.

Let us determine the drag force D on the sphere. One way to do this is to apply

the principle of mechanical energy balance over the entire ﬂow ﬁeld given in equa-

tion (4.63). This requires

DU =



φdV,

which states that the work done by the sphere equals the viscous dissipation over the

entire ﬂow; here, φ is the viscous dissipation per unit volume. A more direct way to

determine the drag is to integrate the stress over the surface of the sphere. The force

per unit area normal to a surface, whose outward unit normal is n is

= τ

=[−pδ

+ σ

=−pn

+ σ

12. Creeping Flow around a Sphere 325

where τ

is the total stress tensor, and σ

is the viscous stress tensor. The component

of the drag force per unit area in the direction of the uniform stream is therefore

[−p cos θ + σ

cos θ − σ

rθ

sin θ]

r=a

, (9.71)

which can be understood from Figure 9.14. The viscous stress components are

= 2µ

∂u

∂r

= 2µU cos θ



−



rθ

= µ



∂

∂r





∂u

∂θ



=−

3µUa

sin θ,

(9.72)

so that equation (9.71) becomes

3µU

cos

θ +0 +

3µU

sin

θ =

3µU

The drag force is obtained by multiplying this by the surface area 4πa

of the sphere,

which gives

D = 6πµaU, (9.73)

of which one-third is pressure drag and two-thirds is skin friction drag. It follows

that the resistance in a creeping ﬂow is proportional to the velocity; this is known as

Stokes’ law of resistance.

In a well-known experiment to measure the charge of an electron, Millikan used

equation (9.73) to estimate the radius of an oil droplet falling through air. Suppose



is the density of a spherical falling particle and ρ is the density of the surrounding

ﬂuid. Then the effective weight of the sphere is 4πa

g(ρ



− ρ)/3, which is the weight

of the sphere minus the weight of the displaced ﬂuid. The falling body is said to reach

the “terminal velocity” when it no longer accelerates, at which point the viscous drag

equals the effective weight. Then

πa

g(ρ



− ρ) = 6πµaU,

from which the radius a can be estimated.

Millikan was able to deduce the charge on an electron making use of Stokes’ drag

formula by the following experiment. Two horizontal parallel plates can be charged

by a battery (see Fig. 9.15). Oil is sprayed through a very ﬁne hole in the upper plate

and develops static charge (+) by losing a few (n) electrons in passing through the

small hole. If the plates are charged, then an electric force neE will act on each of

the drops. Now n is not known but E =−V

/L, where V

is the battery voltage

and L is the gap between the plates, provided that the charge density in the gap is

very low. With the plates uncharged, measurement of the downward terminal velocity

allowed the radius of a drop to be calculated assuming that the viscosity of the drop

is much larger than the viscosity of the air. The switch is thrown to charge the upper

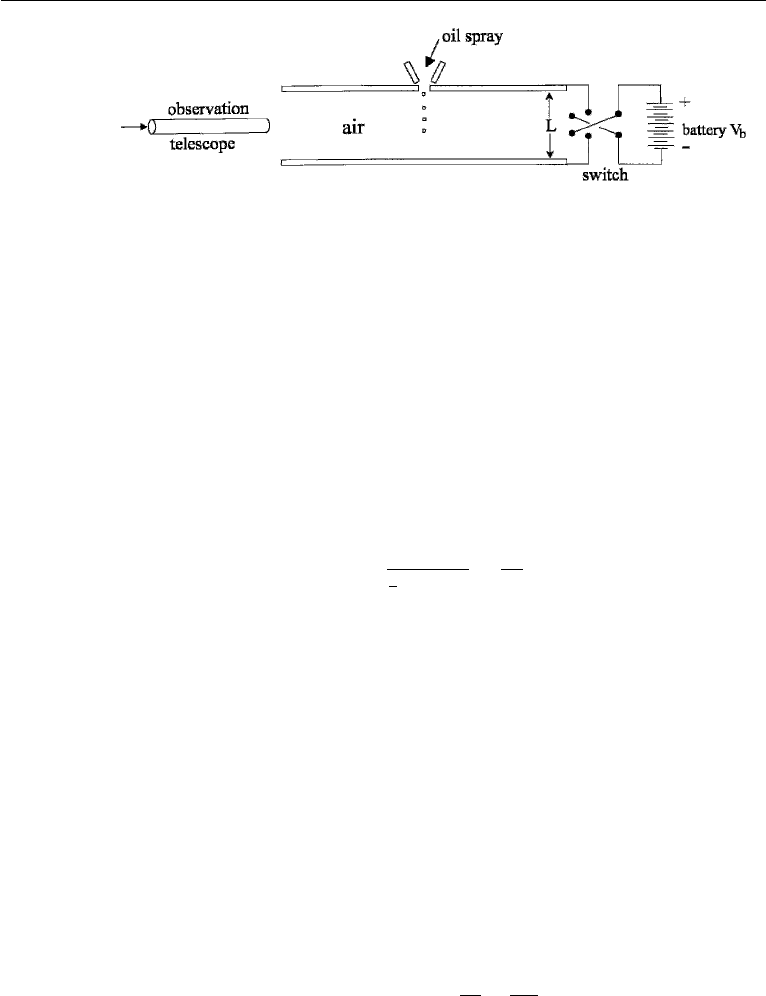
326 Laminar Flow

Figure 9.15 Millikan oil drop experiment.

plate negatively. The same droplet then reverses direction and is forced upwards. It

quickly achieves its terminal velocity U

by virtue of the balance of upward forces

(electric + buoyancy) and downward forces (weight + drag). This gives

6πµU

a + (4/3)π a

g(ρ



− ρ) = neE,

where U

is measured by the observation telescope and the radius of the particle is

now known. The data then allow for the calculation of ne.Asn must be an integer,

data from many droplets may be differenced to identify the minimum difference that

must be e, the charge of a single electron.

The drag coefﬁcient, deﬁned as the drag force nondimensionalized by ρU

and the projected area πa

,is

≡

ρU

πa

, (9.74)

where Re = 2aU/ν is the Reynolds number based on the diameter of the sphere.

In Chapter 8, Section 5 it was shown that dimensional considerations alone require

that C

should be inversely proportional to Re for creeping motions. To repeat the

argument, the drag force in a “massless” ﬂuid (that is, Re  1) can only have the

dependence

D = f(µ,U,a).

The preceding relation involves four variables and the three basic dimensions of mass,

length, and time. Therefore, only one nondimensional parameter, namely, D/µU a,

can be formed. As there is no second nondimensional parameter for it to depend on,

D/µU a must be a constant. This leads to C

∝ 1/Re.

The ﬂow pattern in a reference frame ﬁxed to the ﬂuid at inﬁnity can be found

by superposing a uniform velocity U to the left. This cancels out the ﬁrst term in

equation (9.68), giving

ψ = Ur

sin



−



which gives the streamline pattern as seen by an observer if the sphere is dragged

in front of him from right to left (Figure 9.16). The pattern is symmetric between

the upstream and the downstream directions, which is a result of the linearity of the

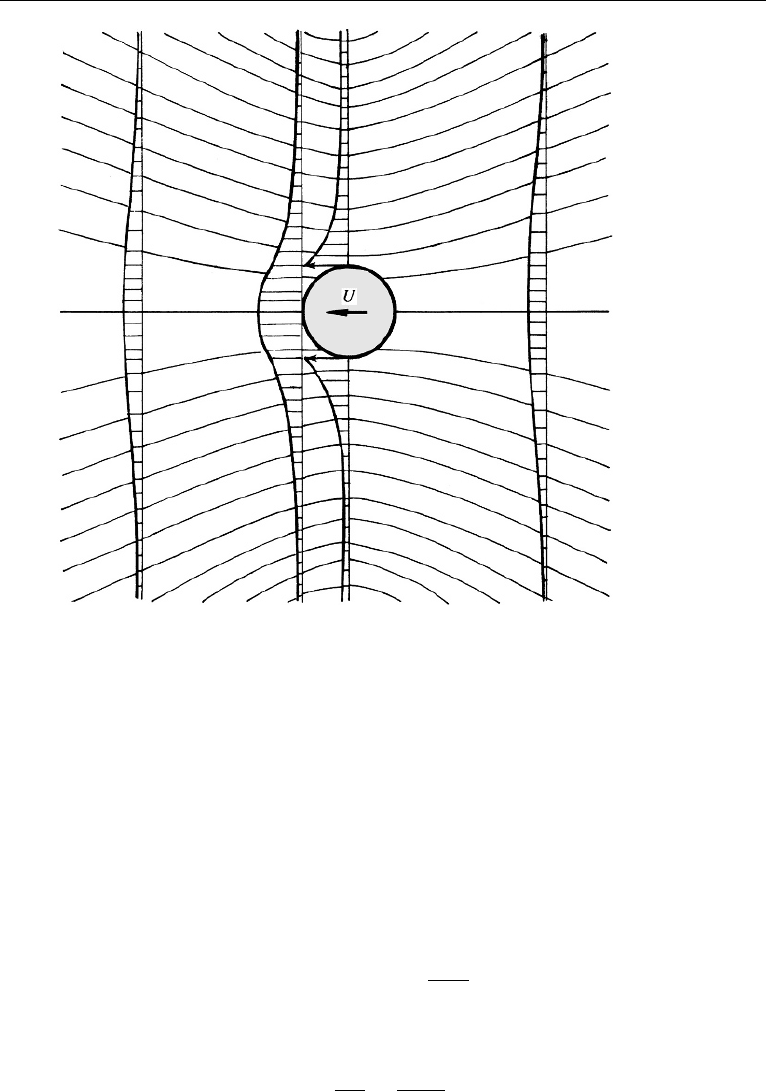
13. Nonuniformity of Stokes’ Solution and Oseen’s Improvement 327

Figure 9.16 Streamlines and velocity distributions in Stokes’ solution of creeping ﬂow due to a moving

sphere. Note the upstream and downstream symmetry, which is a result of complete neglect of nonlinearity.

governing equation (9.63); reversing the direction of the free-stream velocity merely

changes u to −u and p to −p. The ﬂow therefore does not have a “wake” behind the

sphere.

13. Nonuniformity of Stokes’ Solution and

Oseen’s Improvement

The Stokes solution for a sphere is not valid at large distances from the body because

the advective terms are not negligible compared to the viscous terms at these distances.

From equation (9.72), the largest viscous term is of the order

viscous force/volume = stress gradient ∼

µUa

as r →∞,

while from equation (9.69) the largest inertia force is

inertia force/volume ∼ ρu

∂u

∂r

∼

ρU

as r →∞.

328 Laminar Flow

Therefore,

inertia force

viscous force

∼

ρUa

=

as r →∞.

This shows that the inertia forces are not negligible for distances larger than r/a ∼

1/Re. At sufﬁciently large distances, no matter how small Re may be, the neglected

terms become arbitrarily large.

Solutions of problems involving a small parameter can be developed in terms

of the perturbation series in which the higher-order terms act as corrections on the

lower-order terms. Perturbation expansions are discussed brieﬂy in the following

chapter. If we regard the Stokes solution as the ﬁrst term of a series expansion in the

small parameter Re, then the expansion is “nonuniform” because it breaks down at

inﬁnity. If we tried to calculate the next term (to order Re) of the perturbation series,

we would ﬁnd that the velocity corresponding to the higher-order term becomes

unbounded at inﬁnity.

The situation becomes worse for two-dimensional objects such as the circular

cylinder. In this case, the Stokes balance ∇ p = µ∇

u has no solution at all that can

satisfy the uniform ﬂow boundary condition at inﬁnity. From this, Stokes concluded

that steady, slow ﬂows around cylinders cannot exist in nature. It has now been realized

that the nonexistence of a ﬁrst approximation of the Stokes ﬂow around a cylinder is

due to the singular nature of low Reynolds number ﬂows in which there is a region

of nonuniformity at inﬁnity. The nonexistence of the second approximation for ﬂow

around a sphere is due to the same reason. In a different (and more familiar) class

of singular perturbation problems, the region of nonuniformity is a thin layer (the

“boundary layer”) near the surface of an object. This is the class of ﬂows with Re →

∞, that will be discussed in the next chapter. For these high Reynolds number ﬂows

the small parameter 1/Re multiplies the highest-order derivative in the governing

equations, so that the solution with 1/Re identically set to zero cannot satisfy all

the boundary conditions. In low Reynolds number ﬂows this classic symptom of

the loss of the highest derivative is absent, but it is a singular perturbation problem

nevertheless.

In 1910 Oseen provided an improvement to Stokes’ solution by partly accounting

for the inertia terms at large distances. He made the substitutions

u = U + u



v = v



w = w



where (u



) are the Cartesian components of the perturbation velocity, and are

small at large distances. Substituting these, the advection term of the x-momentum

equation becomes

∂u

∂x

+ v

∂u

∂y

+ w

∂u

∂z

= U

∂u



∂x





∂u



∂x

+ v



∂u



∂y

+ w



∂u



∂z



Neglecting the quadratic terms, the equation of motion becomes

ρU

∂u



∂x

=−

∂p

∂x

+ µ∇



13. Nonuniformity of Stokes’ Solution and Oseen’s Improvement 329

where u



represents u



, v



,orw



. This is called Oseen’s equation, and the approxima-

tion involved is called Oseen’s approximation. In essence, the Oseen approximation

linearizes the advective term u

•

∇u by U(∂u/∂x), whereas the Stokes approximation

drops advection altogether. Near the body both approximations have the same order

of accuracy. However, the Oseen approximation is better in the far ﬁeld where the

velocity is only slightly different than U . The Oseen equations provide a lowest-order

solution that is uniformly valid everywhere in the ﬂow ﬁeld.

The boundary conditions for a moving sphere are



= v



= w



= 0 at inﬁnity



=−U, v



= w



= 0 at surface.

The solution found by Oseen is





sin

θ −

(1 + cos θ)



1 − exp



−

(1 − cos θ)



(9.75)

where Re = 2aU/ν is the Reynolds number based on diameter. Near the surface

r/a ≈ 1, and a series expansion of the exponential term shows that Oseen’s solution

is identical to the Stokes solution (9.68) to the lowest order. The Oseen approximation

predicts that the drag coefﬁcient is



1 +



which should be compared with the Stokes formula (9.74). Experimental results (see

Figure 10.22 in the next chapter) show that the Oseen and the Stokes formulas for

are both fairly accurate for Re < 5.

The streamlines corresponding to the Oseen solution (9.75) are shown in

Figure 9.17, where a uniform ﬂow of U is added to the left so as to generate the

pattern of ﬂow due to a sphere moving in front of a stationary observer. It is seen

that the ﬂow is no longer symmetric, but has a wake where the streamlines are closer

together than in the Stokes ﬂow. The velocities in the wake are larger than in front of

the sphere. Relative to the sphere, the ﬂow is slower in the wake than in front of the

sphere.

In 1957, Oseen’s correction to Stokes’ solution was rationalized independently

by Kaplun and Proudman and Pearson in terms of matched asymptotic expansions.

Here, we will obtain only the ﬁrst-order correction. The full vorticity equation is

∇×∇×ω = Re∇×(u × ω). (9.76)

In terms of the Stokes streamfunction ψ, equation (9.64) is generalized to

ψ = Re



∂(ψ,D

ψ)

∂(r,µ)

ψLψ



, (9.77)

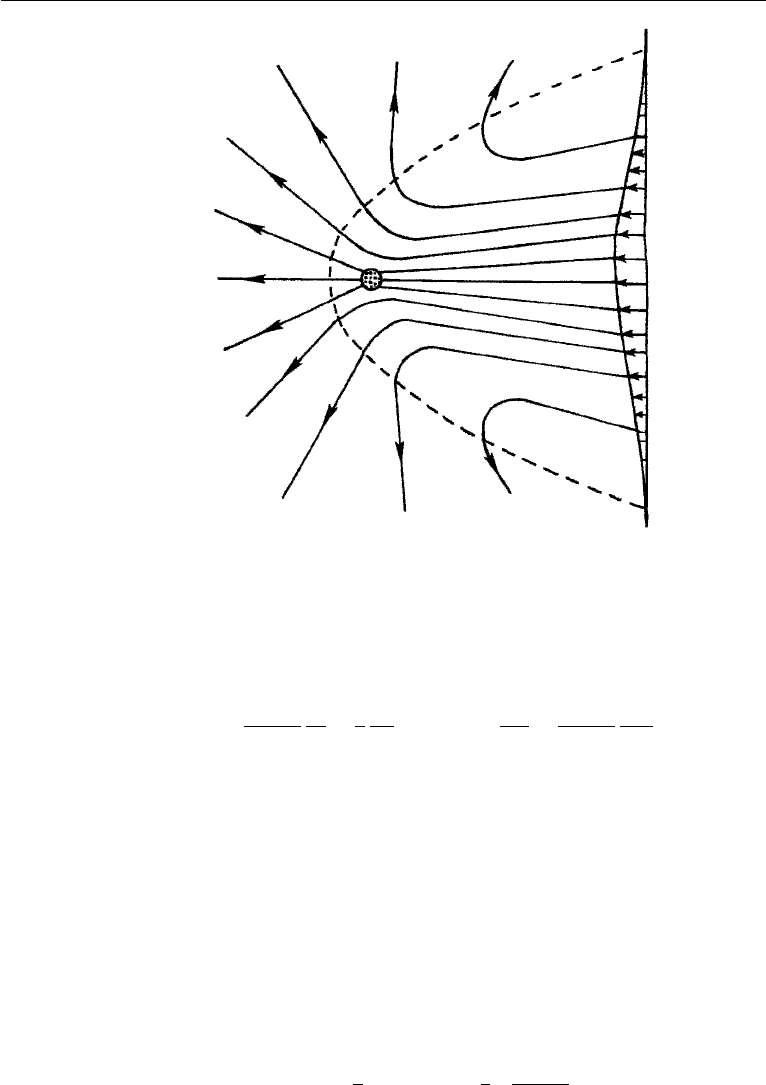
330 Laminar Flow

Figure 9.17 Streamlines and velocity distribution in Oseen’s solution of creeping ﬂow due to a moving

sphere. Note the upstream and downstream asymmetry, which is a result of partial accounting for advection

in the far ﬁeld.

where ∂(ψ,D

ψ)/∂(r, µ) is shorthand notation for the Jacobian determinant with

those four elements, µ = cos θ , and the operators are

L =

1 − µ

∂

∂r

∂

∂µ

∂

∂r

1 − µ

∂

∂µ

We have seen that the right-hand side of equation (9.76) or (9.77) becomes of the

same order as the left-hand side when Re r/a ∼ 1orr/a ∼ 1/Re. We will deﬁne

the “inner region” as r/a  1/Re so that Stokes’ solution holds approximately. To

obtain a better approximation in the inner region, we will write

ψ(r,µ;Re) = ψ

(r, µ) + Re ψ

(r, µ) + o(Re), (9.78)

where the second correction “o(Re)” means that it tends to zero faster than Re in

the limit Re → 0. (See Chapter 10, Section 12. Here ψ is made dimensionless by

and Re = Ua/ν.) Substituting equation (9.78) into (9.77) and taking the limit

Re → 0, we obtain D

= 0 and recover Stokes’ result

=−



− 3r +



− 1

. (9.79)

13. Nonuniformity of Stokes’ Solution and Oseen’s Improvement 331

Subtracting this, dividing by Re and taking the limit Re → 0, we obtain

∂(ψ

)

∂(r,µ)

Lψ

which reduces to



−



µ(µ

− 1), (9.80)

by using equation (9.79). This has the solution

= C



− 3r +



− 1



− 3r + 1 −



µ(µ

− 1)

(9.81)

where C

is a constant of integration for the solution to the homogeneous equation

and is to be determined by matching with the outer region solution.

In the outer region rRe = ρ is ﬁnite. The lowest-order outer solution must be

uniform ﬂow. Then we write the streamfuntion as

(ρ, θ;Re) =

sin

θ +



(ρ, θ ) + o





Substituting in equation (9.77) and taking the limit Re → 0 yields



− cos θ

∂

∂ρ

sin θ

∂

∂θ





= 0, (9.82)

where the operator

= ∂

/∂ρ

sin θ



∂

∂θ

sin θ

∂

∂θ



The solution to equation (9.82) is found to be



(ρ, θ ) =−2C

(1 + cos θ)[1 − e

−ρ(1−cos θ)/2

where the constant of integration C

is determined by matching in the overlap region

between the inner and outer regions: 1  r  1/Re, Re  ρ  1.

The matching gives C

= 3/4 and C

=−3/16. Using this in equation (9.81)

for the inner region solution, the O(Re) correction to the stream function (equa-

tion (9.81)) has been obtained, from which the velocity components, shear stress, and

pressure may be derived. Integrating over the surface of the sphere of radius = a,we

obtain the ﬁnal result for the drag force

D = 6πµUa[1 + 3Ua/(8ν)],

which is consistent with Oseen’s result. Higher-order corrections were obtained by

Chester and Breach (1969).