Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

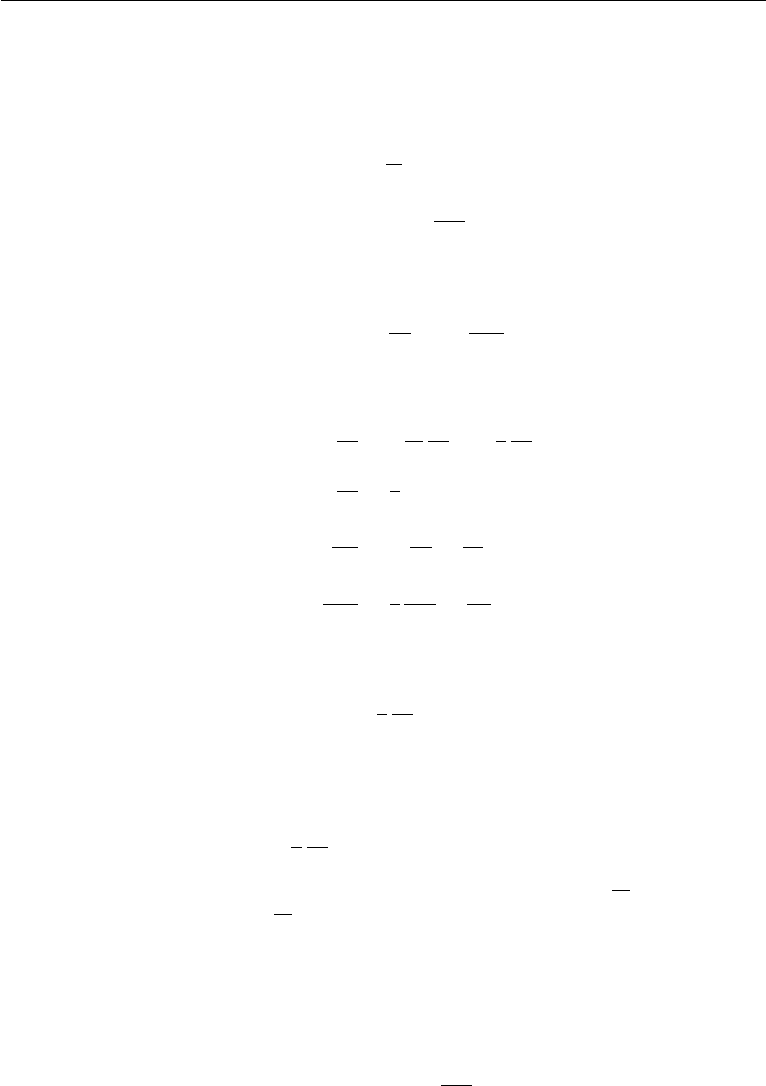
312 Laminar Flow

An Alternative Method of Deducing the Form of η

Instead of arriving at the form of η from dimensional considerations, it could be

derived by a different method as illustrated in the following. Denoting the thickness

of the ﬂow by δ(t), we assume similarity solutions in the form

= F(η),

η =

δ(t)

(9.33)

Then equation (9.17) becomes



∂η

∂t

= νU

∂

∂y

. (9.34)

The derivatives in equation (9.34) are computed from equation (9.33):

∂η

∂t

=−

dδ

=−

dδ

∂η

∂y

∂F

∂y

= F



∂η

∂y



∂

∂y

∂F



∂y



Substitution into equation (9.34) and cancellation of factors give

−



dδ



ηF



= F



Since the right-hand side can only be an explicit function of η, the coefﬁcient in

parentheses on the left-hand side must be independent of t. This requires

dδ

= const. = 2, for example.

Integration gives δ

= 4νt, so that the ﬂow thickness is δ = 2

√

νt. Equation (9.33)

then gives η = y/(2

√

νt), which agrees with our previous ﬁnding.

Method of Laplace Transform

Finally, we shall illustrate the method of Laplace transform for solving the prob-

lem. Let ˆu(y, s) be the Laplace transform of u(y, t). Taking the transform of equa-

tion (9.17), we obtain

s ˆu = ν

ˆu

, (9.35)

8. Diffusion of a Vortex Sheet 313

where the initial condition (9.18) of zero velocity has been used. The transform of

the boundary conditions (9.19) and (9.20) are

ˆu(0,s) =

, (9.36)

ˆu(∞,s)= 0. (9.37)

Equation (9.35) has the general solution

ˆu = Ae

√

s/ν

+ Be

−y

√

s/ν

where the constants A(s) and B(s) are to be determined from the boundary conditions.

The condition (9.37) requires that A = 0, while equation (9.36) requires that B =

U/s. We then have

ˆu =

−y

√

s/ν

The inverse transform of the preceding equation can be found in any mathematical

handbook and is given by equation (9.31).

We have discussed this problem in detail because it illustrates the basic diffusive

nature of viscous ﬂows and also the mathematical techniques involved in ﬁnding

similarity solutions. Several other problems of this kind are discussed in the following

sections, but the discussions shall be somewhat more brief.

8. Diffusion of a Vortex Sheet

Consider the case in which the initial velocity ﬁeld is in the form of a vortex sheet

with u = U for y>0 and u =−U for y<0. We want to investigate how the vortex

sheet decays by viscous diffusion. The governing equation is

∂u

∂t

= ν

∂

∂y

subject to

u(y, 0) = U sgn(y),

u(∞,t) = U,

u(−∞,t) =−U,

where sgn(y) is the “sign function,” deﬁned as 1 for positive y and −1 for negative

y. As in the previous section, the parameter U can be eliminated from the governing

set by regarding u/U as the dependent variable. Then u/U must be a function of

(y,t,ν), and a dimensional analysis reveals that there must exist a similarity solution

in the form

314 Laminar Flow

= F(η),

η =

√

νt

The detailed arguments for the existence of a solution in this form are given

in the preceding section. Substitution of the similarity form into the governing set

transforms it into the ordinary differential equation



=−2ηF



F(+∞) = 1,

F(−∞) =−1,

whose solution is

F(η) = erf(η).

The velocity distribution is therefore

u = U erf



√

νt



. (9.38)

A plot of the velocity distribution is shown in Figure 9.11. If we deﬁne the width of

the transition layer as the distance between the points where u =±0.95U , then the

Figure 9.11 Viscous decay of a vortex sheet. The right panel shows the nondimensional solution and the

left panel indicates the vorticity distribution at two times.

9. Decay of a Line Vortex 315

corresponding value of η is ± 1.38 and consequently the width of the transition layer

is 5.52

√

νt.

It is clear that the ﬂow is essentially identical to that due to the impulsive start

of a ﬂat plate discussed in the preceding section. In fact, each half of Figure 9.11

is identical to Figure 9.10 (within an additive constant of ±1). In both problems

the initial delta-function-like vorticity is diffused away. In the present problem the

magnitude of vorticity at any time is

ω =

∂u

∂y

√

πνt

−y

/4νt

. (9.39)

This is a Gaussian distribution, whose width increases with time as

√

t, while the

maximum value decreases as 1/

√

t. The total amount of vorticity is



∞

−∞

ωdy = 2

√

νt



∞

−∞

ωdη =

√



∞

−∞

−η

dη = 2U,

which is independent of time, and equals the y-integral of the initial (delta-function-

like) vorticity.

9. Decay of a Line Vortex

In Section 6 it was shown that when a solid cylinder of radius R is rotated at angu-

lar speed  in a viscous ﬂuid, the resulting motion is irrotational with a velocity

distribution u

= R

/r. The velocity distribution can be written as



2πr

where  = 2πR

is the circulation along any path surrounding the cylinder. Sup-

pose the radius of the cylinder goes to zero while its angular velocity correspondingly

increases in such a way that the product  = 2πR

is unchanged. In the limit we

obtain a line vortex of circulation , which has an inﬁnite velocity discontinuity at

the origin.

Now suppose that the limiting (inﬁnitely thin and fast) cylinder suddenly stops

rotating at t = 0, thereby reducing the velocity at the origin to zero impulsively. Then

the ﬂuid would gradually slow down from the initial distribution because of viscous

diffusion from the region near the origin. The ﬂow can therefore be regarded as that of

the viscous decay of a line vortex, for which all the vorticity is initially concentrated

at the origin. The problem is the circular analog of the decay of a plane vortex sheet

discussed in the preceding section.

Employing cylindrical coordinates, the governing equation is

∂u

∂t

= ν

∂

∂r



∂

∂r

(ru

)



, (9.40)

316 Laminar Flow

subject to

(r, 0) = /2πr, (9.41)

(0,t) = 0, (9.42)

(r →∞,t) = /2πr. (9.43)

We expect similarity solutions here because there are no natural scales for r and t

introduced from the boundary conditions. Conditions (9.41) and (9.43) show that the

dependence of the solution on the parameter /2πr can be eliminated by deﬁning a

nondimensional velocity



≡

/2πr

, (9.44)

which must have a dependence of the form



= f(r,t,ν).

As the left-hand side of the preceding equation is nondimensional, the right-hand side

must be a nondimensional function of r, t , and ν. A dimensional analysis quickly

shows that the only nondimensional group formed from these is r/

√

νt. Therefore,

the problem must have a similarity solution of the form



= F(η),

η =

4νt

(9.45)

(Note that we could have deﬁned η = r/2

√

νt as in the previous problems, but the

algebra is slightly simpler if we deﬁne it as in equation (9.45).) Substitution of the

similarity solution (9.45) into the governing set (9.40)–(9.43) gives



+ F



= 0,

subject to

F(∞) = 1,

F(0) = 0.

The solution is

F = 1 − e

−η

The dimensional velocity distribution is therefore



2πr

[1 − e

−r

/4νt

]. (9.46)

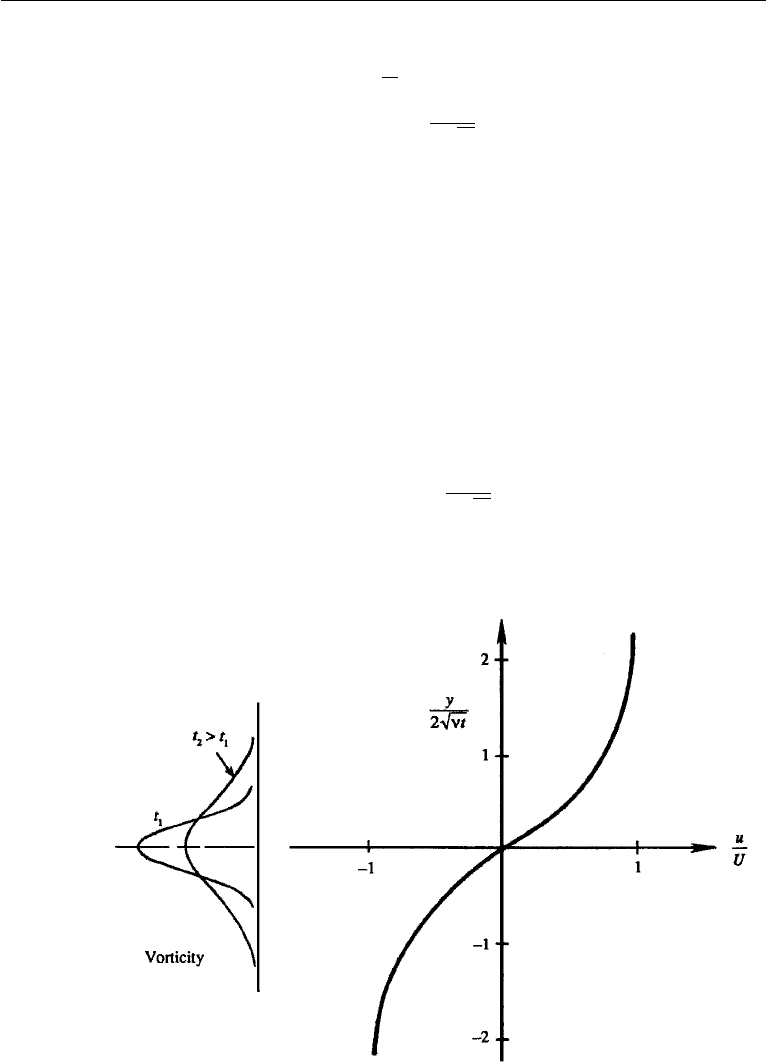
A sketch of the velocity distribution for various values of t is given in Figure 9.12.

Near the center (r  2

√

νt) the ﬂow has the form of a rigid-body rotation, while in

the outer region (r  2

√

νt) the motion has the form of an irrotational vortex.

10. Flow Due to an Oscillating Plate 317

Figure 9.12 Viscous decay of a line vortex showing the tangential velocity at different times.

The foregoing discussion applies to the decay of a line vortex. Consider now

the case where a line vortex is suddenly introduced into a ﬂuid at rest. This can be

visualized as the impulsive start of an inﬁnitely thin and fast cylinder. It is easy to

show that the velocity distribution is (Exercise 5)



2πr

−r

/4νt

, (9.47)

which should be compared to equation (9.46). The analogous problem in heat con-

duction is the sudden introduction of an inﬁnitely thin and hot cylinder (containing a

ﬁnite amount of heat) into a liquid having a different temperature.

10. Flow Due to an Oscillating Plate

The unsteady parallel ﬂows discussed in the three preceding sections had similarity

solutions, because there were no natural scales in space and time. We now discuss

an unsteady parallel ﬂow that does not have a similarity solution because of the

existence of a natural time scale. Consider an inﬁnite ﬂat plate that executes sinusoidal

oscillations parallel to itself. (This is sometimes called Stokes’ second problem.) Only

the steady periodic solution after the starting transients have died will be considered;

thus there are no initial conditions to satisfy. The governing equation is

∂u

∂t

= ν

∂

∂y

, (9.48)

318 Laminar Flow

subject to

u(0,t) = U cos ωt, (9.49)

u(∞,t) = bounded . (9.50)

In the steady state, the ﬂow variables must have a periodicity equal to the periodicity

of the boundary motion. Consequently, we use a separable solution of the form

u = e

iωt

f(y), (9.51)

where what is meant is the real part of the right-hand side. (Such a complex form

of representation is discussed in Chapter 7, Section 15.) Here, f(y) is complex,

thus u(y, t) is allowed to have a phase difference with the wall velocity U cos ωt.

Substitution of equation (9.51) into the governing equation (9.48) gives

iωf = ν

. (9.52)

This is an equation with constant coefﬁcients and must have exponential solu-

tions. Substitution of a solution of the form f = exp(ky) gives k =

√

iω/ν =

±(i + 1)

√

ω/2ν, where the two square roots of i have been used. Consequently,

the solution of equation (9.52) is

f(y) = Ae

−(1+i)y

√

ω/2ν

+ Be

(1+i)y

√

ω/2ν

. (9.53)

The condition (9.50), which requires that the solution must remain bounded at y =∞,

needs B = 0. The solution (9.51) then becomes

u = Ae

iωt

−(1+i)y

√

ω/2ν

. (9.54)

The surface boundary condition (9.49) now gives A = U . Taking the real part of

equation (9.54), we ﬁnally obtain the velocity distribution for the problem:

u = Ue

−y

√

ω/2ν

cos



ωt − y



2ν



. (9.55)

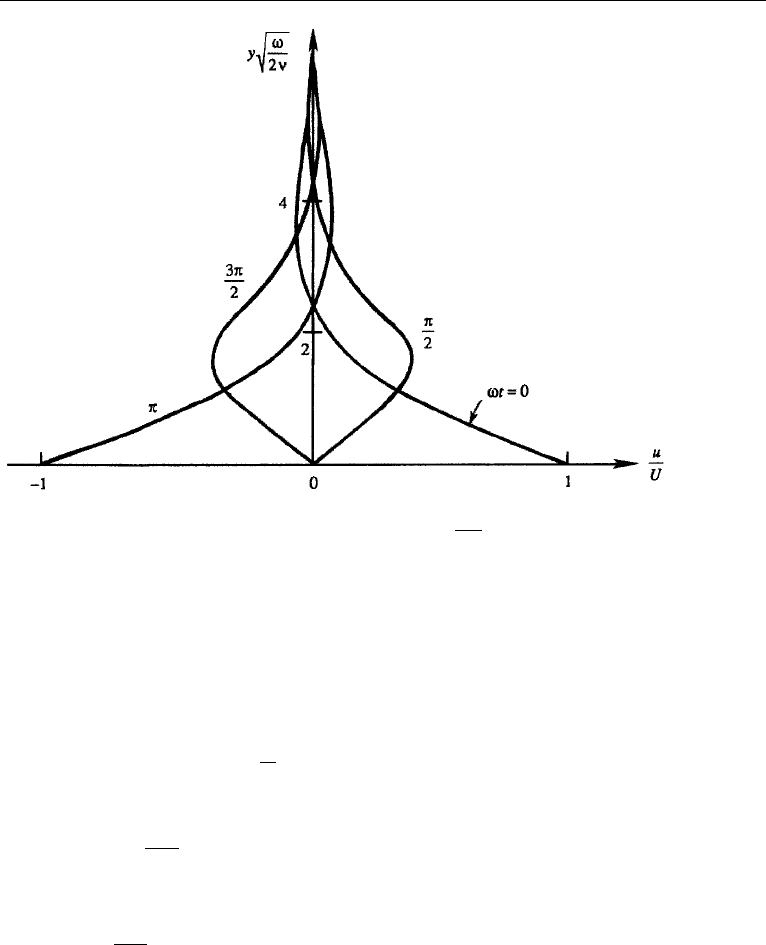
The cosine term in equation (9.55) represents a signal propagating in the direction

of y, while the exponential term represents a decay in y. The ﬂow therefore resem-

bles a damped wave (Figure 9.13). However, this is a diffusion problem and not a

wave-propagation problem because there are no restoring forces involved here. The

apparent propagation is merely a result of the oscillating boundary condition. For

y = 4

√

ν/ω, the amplitude of u is U exp(−4/

√

2) = 0.06U, which means that the

inﬂuence of the wall is conﬁned within a distance of order

δ ∼ 4



ν/ω, (9.56)

which decreases with frequency.

10. Flow Due to an Oscillating Plate 319

Figure 9.13 Velocity distribution in laminar ﬂow near an oscillating plate. The distributions at ωt = 0,

π/2, π, and 3π/2 are shown. The diffusive distance is of order δ = 4

√

ν/ω.

Note that the solution (9.55) cannot be represented by a single curve in terms of

the nondimensional variables. This is expected because the frequency of the bound-

ary motion introduces a natural time scale 1/ω into the problem, thereby violating

the requirements of self-similarity. There are two parameters in the governing set

(9.48)–(9.50), namely, U and ω. The parameter U can be eliminated by regarding

u/U as the dependent variable. Thus the solution must have a form

= f (y, t, ω,ν). (9.57)

As there are ﬁve variables and two dimensions involved, it follows that there must

be three dimensionless variables. A dimensional analysis of equation (9.57) gives

u/U , ωt, and y

√

ω/ν as the three nondimensional variables as in equation (9.55).

Self-similar solutions exist only when there is an absence of such naturally occurring

scales requiring a reduction in the dimensionality of the space.

An interesting point is that the oscillating plate has a constant diffusion dis-

tance δ = 4

√

ν/ω that is in contrast to the case of the impulsively started plate

in which the diffusion distance increases with time. This can be understood from

the governing equation (9.48). In the problem of sudden acceleration of a plate,

∂

u/∂y

is positive for all y (see Figure 9.10), which results in a positive ∂u/∂t

everywhere. The monotonic acceleration signiﬁes that momentum is constantly

diffused outward, which results in an ever-increasing width of ﬂow. In contrast,

in the case of an oscillating plate, ∂

u/∂y

(and therefore ∂u/∂t) constantly

320 Laminar Flow

changes sign in y and t. Therefore, momentum cannot diffuse outward monotonically,

which results in a constant width of ﬂow.

The analogous problem in heat conduction is that of a semi-inﬁnite solid, the

surface of which is subjected to a periodic ﬂuctuation of temperature. The resulting

solution, analogous to equation (9.55), has been used to estimate the effective “eddy”

diffusivity in the upper layer of the ocean from measurements of the phase difference

(that is, the time lag between maxima) between the temperature ﬂuctuations at two

depths, generated by the diurnal cycle of solar heating.

11. High and Low Reynolds Number Flows

Many physical problems can be described by the behavior of a system when a certain

parameter is either very small or very large. Consider the problem of steady ﬂow

around an object described by

ρu

•

∇u =−∇p + µ∇

u. (9.58)

First, assume that the viscosity is small. Then the dominant balance in the ﬂow is

between the pressure and inertia forces, showing that pressure changes are of order

ρU

. Consequently, we nondimensionalize the governing equation (9.58) by scaling

u by the free-stream velocity U , pressure by ρU

, and distance by a representative

length L of the body. Substituting the nondimensional variables (denoted by primes)



p − p

∞

ρU

, (9.59)

the equation of motion (9.58) becomes



•

∇u



=−∇p



∇



, (9.60)

where Re = Ul/ν is the Reynolds number. For high Reynolds number ﬂows, equa-

tion (9.60) is solved by treating 1/Re as a small parameter. As a ﬁrst approximation,

we may set 1/Re to zero everywhere in the ﬂow, thus reducing equation (9.60) to

the inviscid Euler equation. However, this omission of viscous terms cannot be valid

near the body because the inviscid ﬂow cannot satisfy the no-slip condition at the

body surface. Viscous forces do become important near the body because of the high

shear in a layer near the body surface. The scaling (9.59), which assumes that veloc-

ity gradients are proportional to U/L, is invalid in the boundary layer near the solid

surface. We say that there is a region of nonuniformity near the body at which point

a perturbation expansion in terms of the small parameter 1/Re becomes singular.

The proper scaling in the boundary layer and the procedure of solving high Reynolds

number ﬂows will be discussed in Chapter 10.

Now consider ﬂows in the opposite limit of very low Reynolds numbers, that is,

→0. It is clear that low Reynolds number ﬂows will have negligible inertia forces

and therefore the viscous and pressure forces should be in approximate balance.

11. High and Low Reynolds Number Flows 321

For the governing equations to display this fact, we should have a small parameter

multiplying the inertia forces in this case. This can be accomplished if the variables are

nondimensionalized properly to take into account the low Reynolds number nature of

the ﬂow. Obviously, the scaling (9.59), which leads to equation (9.60), is inappropriate

in this case. For if equation (9.60) were multiplied by Re, then the small parameter

Re would appear in front of not only the inertia force term but also the pressure force

term, and the governing equation would reduce to 0 = µ∇

u as Re → 0, which is

not the balance for low Reynolds number ﬂows. The source of the inadequacy of the

nondimensionalization (9.59) for low Reynolds number ﬂows is that the pressure is

not of order ρU

in this case. As we noted in Chapter 8, for these external ﬂows,

pressure is a passive variable and it must be normalized by the dominant effect(s),

which here are viscous forces. The purpose of scaling is to obtain nondimensional

variables that are of order one, so that pressure should be scaled by ρU

only in high

Reynolds number ﬂows in which the pressure forces are of the order of the inertia

forces. In contrast, in a low Reynolds number ﬂow the pressure forces are of the

order of the viscous forces. For ∇p to balance µ∇

u in equation (9.58), the pressure

changes must have a magnitude of the order

p ∼ Lµ∇

u ∼ µU/L.

Thus the proper nondimensionalization for low Reynolds number ﬂows is



p − p

∞

µU/L

. (9.61)

The variations of the nondimensional variables u



and p



in the ﬂow ﬁeld are now

of order one. The pressure scaling also shows that p is proportional to µ inalow

Reynolds number ﬂow. A highly viscous oil is used in the bearing of a rotating shaft

because the high pressure developed in the oil ﬁlm of the bearing “lifts” the shaft and

prevents metal-to-metal contact.

Substitution of equation (9.61) into (9.58) gives the nondimensional equation

Re u



•

∇u



=−∇p



+∇



. (9.62)

In the limit Re → 0, equation (9.62) becomes the linear equation

∇p = µ∇

u, (9.63)

where the variables have been converted back to their dimensional form.

Flows at Re  1 are called creeping motions. They can be due to small velocity,

large viscosity, or (most commonly) the small size of the body. Examples of such

ﬂows are the motion of a thin ﬁlm of oil in the bearing of a shaft, settling of sediment

particles near the ocean bottom, and the fall of moisture drops in the atmosphere. In

the next section, we shall examine the creeping ﬂow around a sphere.

Summary: The purpose of scaling is to generate nondimensional variables that

are of order one in the ﬂow ﬁeld (except in singular regions or boundary layers).