Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

292 Dynamic Similarity

7. Signiﬁcance of Common Nondimensional Parameters

So far, we have encountered several nondimensional groups such as the pressure

coefﬁcient (p − p

∞

)/ρU

, the drag coefﬁcient 2D/ρU

, the Reynolds num-

ber Re = Ul/ν, and the Froude number U/

√

gl. Several independent nondi-

mensional parameters that commonly enter ﬂuid ﬂow problems are listed and dis-

cussed brieﬂy in this section. Other parameters will arise throughout the rest of the

book.

Reynolds Number

The Reynolds number is the ratio of inertia force to viscous force:

Re ≡

Inertia force

Viscous force

∝

ρu∂u/∂x

µ∂

u/∂x

∝

ρU

µU/ l

Equality of Re is a requirement for the dynamic similarity of ﬂows in which viscous

forces are important.

Froude Number

The Froude number is deﬁned as

Fr ≡



Inertia force

Gravity force



1/2

∝



ρU

ρg



1/2

√

Equality of Fr is a requirement for the dynamic similarity of ﬂows with a free surface

in which gravity forces are dynamically signiﬁcant. Some examples of ﬂows in which

gravity plays a signiﬁcant role are the motion of a ship, ﬂow in an open channel, and

the ﬂow of a liquid over the spillway of a dam (Figure 8.3).

Internal Froude Number

In a density-stratiﬁed ﬂuid the gravity force can play a signiﬁcant role without the

presence of a free surface. Then the effective gravity force in a two-layer situation is

Figure 8.3 Examples of ﬂows in which gravity is important.

7. Signiﬁcance of Common Nondimensional Parameters 293

the “buoyancy” force (ρ

−ρ

)g, as seen in the preceding chapter. In such a case we

can deﬁne an internal Froude number as



≡



Inertia force

Buoyancy force



1/2

∝



(ρ

− ρ



1/2





, (8.21)

where g



≡ g

(

− ρ

)

/ρ

is the “reduced gravity.” For a continuously stratiﬁed

ﬂuid having a maximum buoyancy frequency N, we similarly deﬁne



≡

which is analogous to equation (8.21) since g



= g

(

− ρ

)

/ρ

is similar to

−ρ

−1

(

dρ/dz

)

l = N

Richardson Number

Instead of deﬁning the internal Froude number, it is more common to deﬁne a non-

dimensional parameter that is equivalent to 1/Fr

2

. This is called the Richardson

number, and in a two-layer situation it is deﬁned as

Ri ≡



. (8.22)

In a continuously stratiﬁed ﬂow, we can similarly deﬁne

Ri ≡

. (8.23)

It is clear that the Richardson number has to be equal for the dynamic similarity of

two density-stratiﬁed ﬂows.

Equations (8.22) and (8.23) deﬁne overall or bulk Richardson numbers in terms

of the scales l, N, and U . In addition, we can deﬁne a Richardson number involving

the local values of velocity gradient and stratiﬁcation at a certain depth z. This is

called the gradient Richardson number, and it is deﬁned as

(

)

≡

(

)

(

dU/dz

)

Local Richardson numbers will be important in our studies of instability and turbu-

lence in stratiﬁed ﬂuids.

Mach Number

The Mach number is deﬁned as

M ≡



Inertia force

Compressibility force



1/2

∝



ρU

ρc



1/2

294 Dynamic Similarity

where c is the speed of sound. Equality of Mach numbers is a requirement for the

dynamic similarity of compressible ﬂows. For example, the drag experienced by a

body in a ﬂow with compressibility effects has the form

= f

(

Re,M

)

Flows in which M<1 are called subsonic, whereas ﬂows in which M>1 are called

supersonic. It will be shown in Chapter 16 that compressibility effects can be neglected

if M<0.3.

Prandtl Number

The Prandtl number enters as a nondimensional parameter in ﬂows involving heat

conduction. It is deﬁned as

Pr ≡

Momentum diffusivity

Heat diffusivity

µ/ρ

k/ρC

It is therefore a ﬂuid property and not a ﬂow variable. For air at ordinary temper-

atures and pressures, Pr = 0.72, which is close to the value of 0.67 predicted from

a simpliﬁed kinetic theory model assuming hard spheres and monatomic molecules

(Hirschfelder, Curtiss, and Bird (1954), pp. 9–16). For water at 20

◦

C, Pr = 7.1. The

dynamic similarity of ﬂows involving thermal effects requires equality of Prandtl

numbers.

Exercises

1. Suppose that the power to drive a propeller of an airplane depends on d

(diameter of the propeller), U (free-stream velocity), ω (angular velocity of pro-

peller), c (velocity of sound), ρ (density of ﬂuid), and µ (viscosity). Find the dimen-

sionless groups. In your opinion, which of these are the most important and should

be duplicated in a model testing?

2. A 1/25 scale model of a submarine is being tested in a wind tunnel in which

p = 200 kPa and T = 300 K. If the prototype speed is 30 km/hr, what should be the

free-stream velocity in the wind tunnel? What is the drag ratio? Assume that the

submarine would not operate near the free surface of the ocean.

Literature Cited

Hirschfelder, J. O., C. F. Curtiss, and R. B. Bird (1954). Molecular Theory of Gases and Liquids, New York:

John Wiley and Sons.

Supplemental Reading

Bridgeman, P. W. (1963). Dimensional Analysis, New Haven: Yale University Press.

Chapter 9

Laminar Flow

1. Introduction.......................... 295

2. Analogy between Heat and Vorticity

Diffusion ............................. 297

3. Pressure Change Due to Dynamic

Effects ............................... 297

4. Steady Flow between Parallel

Plates................................ 298

Plane Couette Flow................... 300

Plane Poiseuille Flow ................. 301

5. Steady Flow in a Pipe ................ 302

6. Steady Flow between Concentric

Cylinders ............................ 303

Flow Outside a Cylinder Rotating in an

Inﬁnite Fluid ...................... 304

Flow Inside a Rotating Cylinder....... 305

7. Impulsively Started Plate: Similarity

Solutions............................. 306

Formulation of a Problem in Similarity

Variables .......................... 306

Similarity Solution .................. 309

An Alternative Method of Deducing

the Form of η ..................... 312

Method of Laplace Transform ....... 312

8. Diffusion of a Vortex Sheet ........... 313

9. Decay of a Line Vortex............... 315

10. Flow Due to an Oscillating

Plate ............................... 317

11. High and Low Reynolds Number

Flows ............................... 320

12. Creeping Flow around a

Sphere .............................. 322

13. Nonuniformity of Stokes’ Solution

and Oseen’s Improvement............ 327

14. Hele-Shaw Flow..................... 332

15. Final Remarks ....................... 334

Exercises ............................ 335

Literature Cited ..................... 337

Supplemental Reading ............... 337

1. Introduction

In Chapters 6 and 7 we studied inviscid ﬂows in which the viscous terms in the

Navier–Stokes equations were dropped. The underlying assumption was that the vis-

cous forces were conﬁned to thin boundary layers near solid surfaces, so that the

bulk of the ﬂow could be regarded as inviscid (Figure 6.1). We shall see in the next

chapter that this is indeed valid if the Reynolds number is large. For low values of

the Reynolds number, however, the entire ﬂow may be dominated by viscosity, and

the inviscid ﬂow theory is of little use. The purpose of this chapter is to present cer-

tain solutions of the Navier–Stokes equations in some simple situations, retaining the

viscous term µ∇

u everywhere in the ﬂow. While the inviscid ﬂow theory allows the

ﬂuid to “slip” past a solid surface, real ﬂuids will adhere to the surface because of

295

DOI: 10.1016/B978-0-12-381399-2.50009-5

296 Laminar Flow

intermolecular interactions, that is, a real ﬂuid satisﬁes the condition of zero relative

velocity at a solid surface. This is the so-called no-slip condition.

Before presenting the solutions, we shall ﬁrst discuss certain basic ideas about

viscous ﬂows. Flows in which the ﬂuid viscosity is important can be of two types,

namely, laminar and turbulent. The basic difference between the two ﬂows was dra-

matically demonstrated in 1883 by Reynolds, who injected a thin stream of dye into

the ﬂow of water through a tube (Figure 9.1). At low rates of ﬂow, the dye stream

was observed to follow a well-deﬁned straight path, indicating that the ﬂuid moved

in parallel layers (laminae) with no macroscopic mixing motion across the layers.

This is called a laminar ﬂow. As the ﬂow rate was increased beyond a certain critical

value, the dye streak broke up into an irregular motion and spread throughout the

cross section of the tube, indicating the presence of macroscopic mixing motions per-

pendicular to the direction of ﬂow. Such a chaotic ﬂuid motion is called a turbulent

ﬂow. Reynolds demonstrated that the transition from laminar to turbulent ﬂow always

occurred at a ﬁxed value of the ratio Re = Vd/ν ∼ 3000, where V is the velocity

averaged over the cross section, d is the tube diameter, and ν is the kinematic viscosity.

Laminar ﬂows in which viscous effects are important throughout the ﬂow are the

subject of the present chapter; laminar ﬂows in which frictional effects are conﬁned to

boundary layers near solid surfaces are discussed in the next chapter. Chapter 12 con-

siders the stability of laminar ﬂows and their transition to turbulence; fully turbulent

ﬂows are discussed in Chapter 13. We shall assume here that the ﬂow is incompress-

ible, which is valid for Mach numbers less than 0.3. We shall also assume that the

Figure 9.1 Reynolds’s experiment to distinguish between laminar and turbulent ﬂows.

3. Pressure Change Due to Dynamic Effects 297

ﬂow is unstratiﬁed and observed in a nonrotating coordinate system. Some solutions

of viscous ﬂows in rotating coordinates, such as the Ekman layers, are presented in

Chapter 14.

2. Analogy between Heat and Vorticity Diffusion

For two-dimensional ﬂows that take place in the xy-plane, the vorticity equation is

(see equation (5.13))

Dω

= ν∇

ω,

where ω = ∂v/∂x − ∂u/∂y. (For the sake of simplicity, we have avoided the vortex

stretching term ω

•

∇u by assuming two dimensionality.) This shows that the rate of

change of vorticity ∂ω/∂t at a point is due to advection (−u

•

∇ω) and diffusion

(ν∇

ω) of vorticity. The equation is similar to the heat equation

= κ∇

where κ = k/ρC

is the thermal diffusivity. The similarity of the equations suggests

that vorticity diffuses in a manner analogous to the diffusion of heat. The similarity

also brings out the fact that the diffusive effects are controlled by ν and κ, and not by

µ and k. In fact, the momentum equation

= ν∇

u −

∇p, (9.1)

also shows that the acceleration due to viscous diffusion is proportional to ν. Thus,

air (ν = 15 × 10

−6

/s) is more diffusive than water (ν = 10

−6

/s), although µ

for water is larger. Both ν and κ have the units of m

/s; the kinematic viscosity ν is

therefore also called momentum diffusivity, in analogy with κ, which is called heat dif-

fusivity. (However, velocity cannot be simply regarded as being diffused and advected

in a ﬂow because of the presence of the pressure gradient term in equation (9.1). The

analogy between heat and vorticity is more appropriate.)

3. Pressure Change Due to Dynamic Effects

The equation of motion for the ﬂow of a uniform density ﬂuid is

= ρg − ∇p + µ∇

If the body of ﬂuid is at rest, the pressure is hydrostatic:

0 = ρg − ∇p

Subtracting, we obtain

=−∇p

+ µ∇

u, (9.2)

298 Laminar Flow

where p

≡ p − p

is the pressure change due to dynamic effects. As there is no

accepted terminology for p

, we shall call it dynamic pressure, although the term is

also used for ρq

/2, where q is the speed. Other common terms for p

are “modiﬁed

pressure” (Batchelor, 1967) and “excess pressure” (Lighthill, 1986).

For a ﬂuid of uniform density, introduction of p

eliminates gravity from the dif-

ferential equation as in equation (9.2). However, the process may not eliminate gravity

from the problem. Gravity reappears in the problem if the boundary conditions are

given in terms of the total pressure p. An example is the case of surface gravity waves,

where the total pressure is ﬁxed at the free surface, and the mere introduction of p

does not eliminate gravity from the problem. Without a free surface, however, gravity

has no dynamic role. Its only effect is to add a hydrostatic contribution to the pressure

ﬁeld. In the applications that follow, we shall use equation (9.2), but the subscript on

p will be omitted, as it is understood that p stands for the dynamic pressure.

4. Steady Flow between Parallel Plates

Because of the presence of the nonlinear advection term u

•

∇u, very few exact

solutions of the Navier–Stokes equations are known in closed form. In general, exact

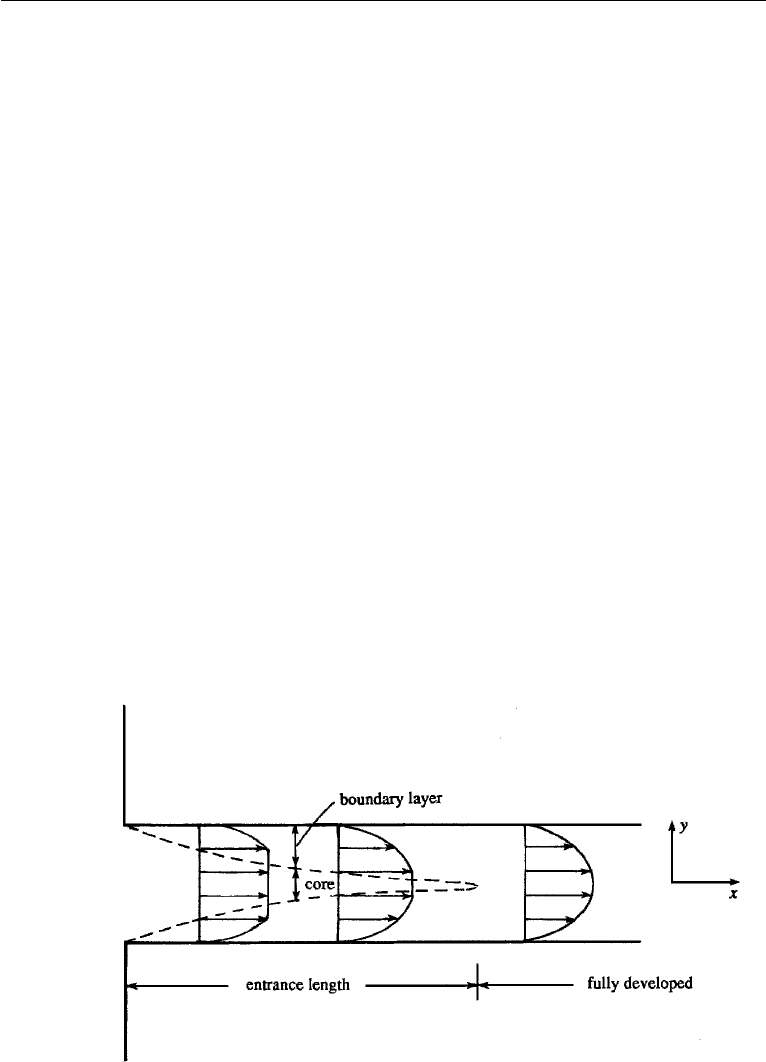
solutions are possible only when the nonlinear terms vanish identically. An example is

the fully developed ﬂow between inﬁnite parallel plates. The term “fully developed”

signiﬁes that we are considering regions beyond the developing stage near the entrance

(Figure 9.2), where the velocity proﬁle changes in the direction of ﬂow because of the

development of boundary layers from the two walls. Within this “entrance length,”

which can be several times the distance between the walls, the velocity is uniform in

the core increasing downstream and decreasing with x within the boundary layers. The

derivative ∂u/∂x is therefore nonzero; the continuity equation ∂u/∂x + ∂v/∂y = 0

Figure 9.2 Developing and fully developed ﬂows in a channel. The ﬂow is fully developed after the

boundary layers merge.

4. Steady Flow between Parallel Plates 299

then requires that v = 0, so that the ﬂow is not parallel to the walls within the entrance

length.

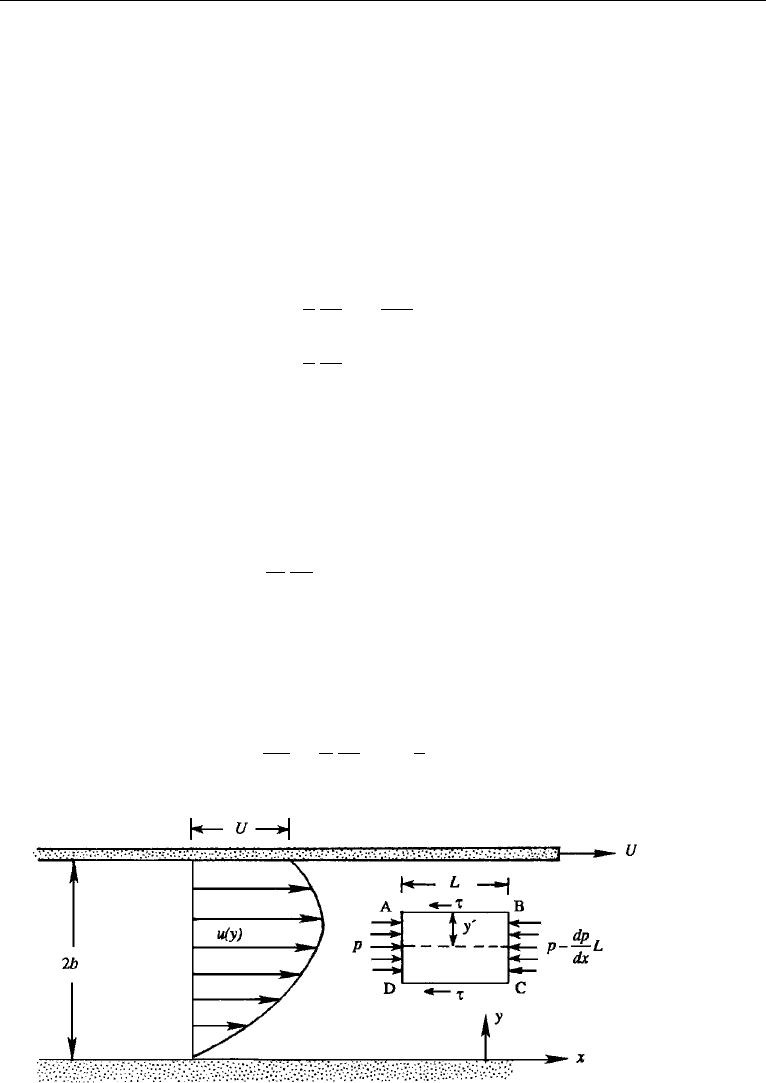
Consider the fully developed stage of the steady ﬂow between two inﬁnite parallel

plates. The ﬂow is driven by a combination of an externally imposed pressure gradient

(for example, maintained by a pump) and the motion of the upper plate at uniform

speed U . Take the x-axis along the lower plate and in the direction of ﬂow (Figure 9.3).

Two dimensionality of the ﬂow requires that ∂/∂z = 0. Flow characteristics are also

invariant in the x direction, so that continuity requires ∂v/∂y = 0. Since v = 0at

y = 0, it follows that v = 0 everywhere, which reﬂects the fact that the ﬂow is parallel

to the walls. The x- and y-momentum equations are

0 =−

∂p

∂x

+ ν

0 =−

∂p

∂y

The y-momentum equation shows that p is not a function of y. In the x-momentum

equation, then, the ﬁrst term can only be a function of x, while the second term can

only be a function of y. The only way this can be satisﬁed is for both terms to be

constant. The pressure gradient is therefore a constant, which implies that the pressure

varies linearly along the channel. Integrating the x-momentum equation twice, we

obtain

0 =−

+ µu + Ay + B, (9.3)

where we have written dp/dx because p is a function of x alone. The constants of

integration A and B are determined as follows. The lower boundary condition u = 0

at y = 0 requires B = 0. The upper boundary condition u = U at y = 2b requires

A = b(dp/dx) − µU/2b. The velocity proﬁle equation (9.3) then becomes

u =

−



b −



. (9.4)

Figure 9.3 Flow between parallel plates.

300 Laminar Flow

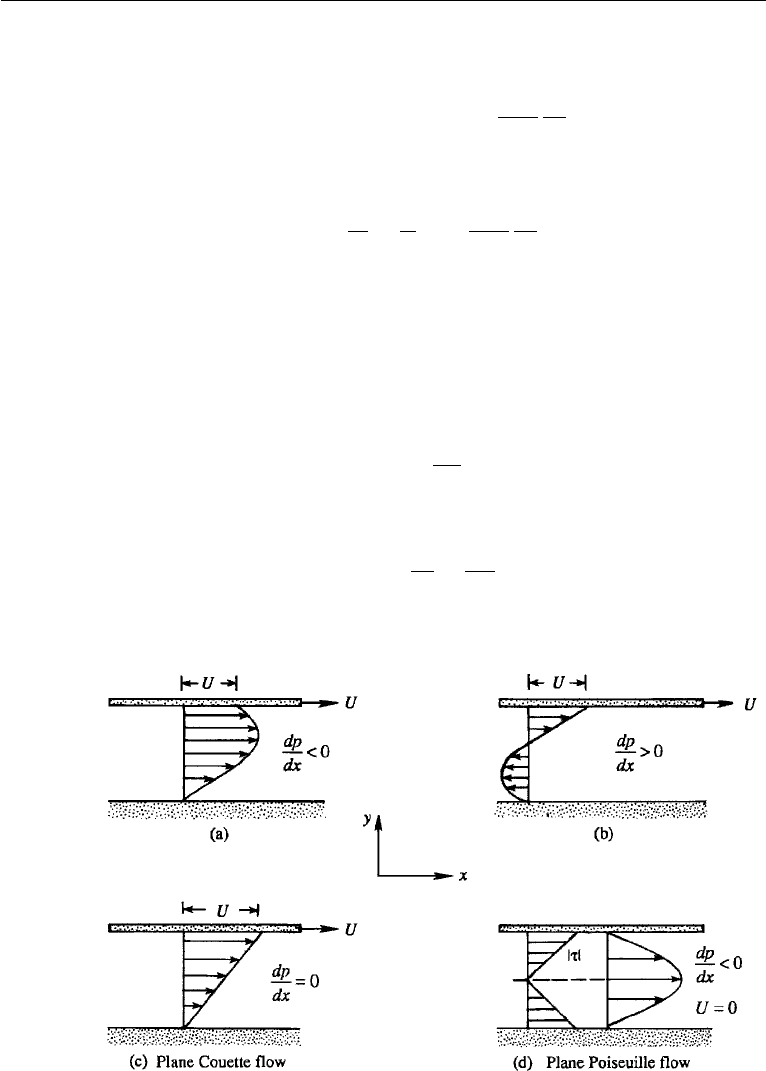
The velocity proﬁle is illustrated in Figure 9.4 for various cases.

The volume rate of ﬂow per unit width of the channel is

Q =



udy= Ub



1 −

3µU



so that the average velocity is

V ≡



1 −

3µU



Two cases of special interest are discussed in what follows.

Plane Couette Flow

The ﬂow driven by the motion of the upper plate alone, without any externally imposed

pressure gradient, is called a plane Couette ﬂow. In this case equation (9.4) reduces

to the linear proﬁle (Figure 9.4c)

u =

. (9.5)

The magnitude of shear stress is

τ = µ

µU

which is uniform across the channel.

Figure 9.4 Various cases of parallel ﬂow in a channel.

4. Steady Flow between Parallel Plates 301

Plane Poiseuille Flow

The ﬂow driven by an externally imposed pressure gradient through two stationary

ﬂat walls is called a plane Poiseuille ﬂow. In this case equation (9.4) reduces to the

parabolic proﬁle (Figure 9.4d)

u =−



b −



. (9.6)

The magnitude of shear stress is

τ = µ

= (b − y)

which shows that the stress distribution is linear with a magnitude of b(dp/dx) at the

walls (Figure 9.4d).

It is important to note that the constancy of the pressure gradient and the linearity

of the shear stress distribution are general results for a fully developed channel ﬂow

and hold even if the ﬂow is turbulent. Consider a control volume ABCD shown in

Figure 9.3, and apply the momentum principle (see equation (4.20)), which states that

the net force on a control volume is equal to the net outﬂux of momentum through the

surfaces. Because the momentum ﬂuxes across surfaces AD and BC cancel each other,

the forces on the control volume must be in balance; per unit width perpendicular to

the plane of paper, the force balance gives



p −



p −





= 2Lτ, (9.7)

where y



is the distance measured from the center of the channel. In equation (9.7), 2y



is the area of surfaces AD and BC, and L is the area of surface AB or DC. Applying

equation (9.7) at the wall, we obtain

b = τ

, (9.8)

which shows that the pressure gradient dp/dx is constant. Equations (9.7) and (9.8)

give

τ =



, (9.9)

which shows that the magnitude of the shear stress increases linearly from the center

of the channel (Figure 9.4d). Note that no assumption about the nature of the ﬂow

(laminar or turbulent) has been made in deriving equations (9.8) and (9.9).

Instead of applying the momentum principle, we could have reached the forego-

ing conclusions from the equation of motion in the form

=−

dτ