Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

262 Gravity Waves

17. Shallow Layer Overlying an Inﬁnitely Deep Fluid

A very common simpliﬁcation, frequently made in geophysical situations in which

large-scale motions are considered, involves assuming that the wavelengths are large

compared to the upper layer depth. For example, the depth of the oceanic upper layer,

below which there is a sharp density gradient, could be ≈50 m thick, and we may

be interested in interfacial waves that are much longer than this. The approximation

kH  1 is called the shallow-water or long-wave approximation. Using

sinh kH  kH,

cosh kH  1,

the dispersion relation (7.123) corresponding to the baroclinic mode reduces to

gH(ρ

− ρ

)

. (7.125)

The phase velocity of waves at the interface is therefore

c =



H, (7.126)

where we have deﬁned



≡ g



− ρ



(7.127)

which is called the reduced gravity. Equation (7.126) is similar to the correspond-

ing expression for surface waves in a shallow homogeneous layer of thickness H ,

namely, c =

√

gH, except that its speed is reduced by the factor

√

(ρ

− ρ

)/ρ

This agrees with our previous conclusion that internal waves generally propagate

slower than surface waves. Under the shallow-water approximation, equation (7.124)

reduces to

η =−ζ



− ρ



. (7.128)

In Section 6 we noted that, for surface waves, the shallow-water approximation

is equivalent to the hydrostatic approximation, and results in a depth-independent

horizontal velocity. Such a conclusion also holds for interfacial waves. The fact that

is independent of z follows from equation (7.114) on noting that e

 e

−kz

 1. To

see that pressure is hydrostatic, the perturbation pressure in the upper layer determined

from equation (7.114) is



=−ρ

∂φ

∂t

= iρ

ω(A + B)e

i(kx−ωt)

= ρ

gη, (7.129)

18. Equations of Motion for a Continuously Stratiﬁed Fluid 263

where the constants given in equations (7.116) and (7.117) have been used. This

shows that p



is independent of z and equals the hydrostatic pressure change due to

the free surface displacement.

So far, the lower ﬂuid has been assumed to be inﬁnitely deep, resulting in an

exponential decay of the ﬂow ﬁeld from the interface into the lower layer, with a

decay scale of the order of the wavelength. If the lower layer is now considered

thin compared to the wavelength, then the horizontal velocity will be depth indepen-

dent, and the ﬂow hydrostatic, in the lower layer. If both layers are considered thin

compared to the wavelength, then the ﬂow is hydrostatic (and the horizontal veloc-

ity ﬁeld depth-independent) in both layers. This is the shallow-water or long-wave

approximation for a two-layer ﬂuid. In such a case the horizontal velocity ﬁeld in the

barotropic mode has a discontinuity at the interface, which vanishes in the Boussinesq

limit (ρ

− ρ

)/ρ

 1. Under these conditions the two modes of a two-layer sys-

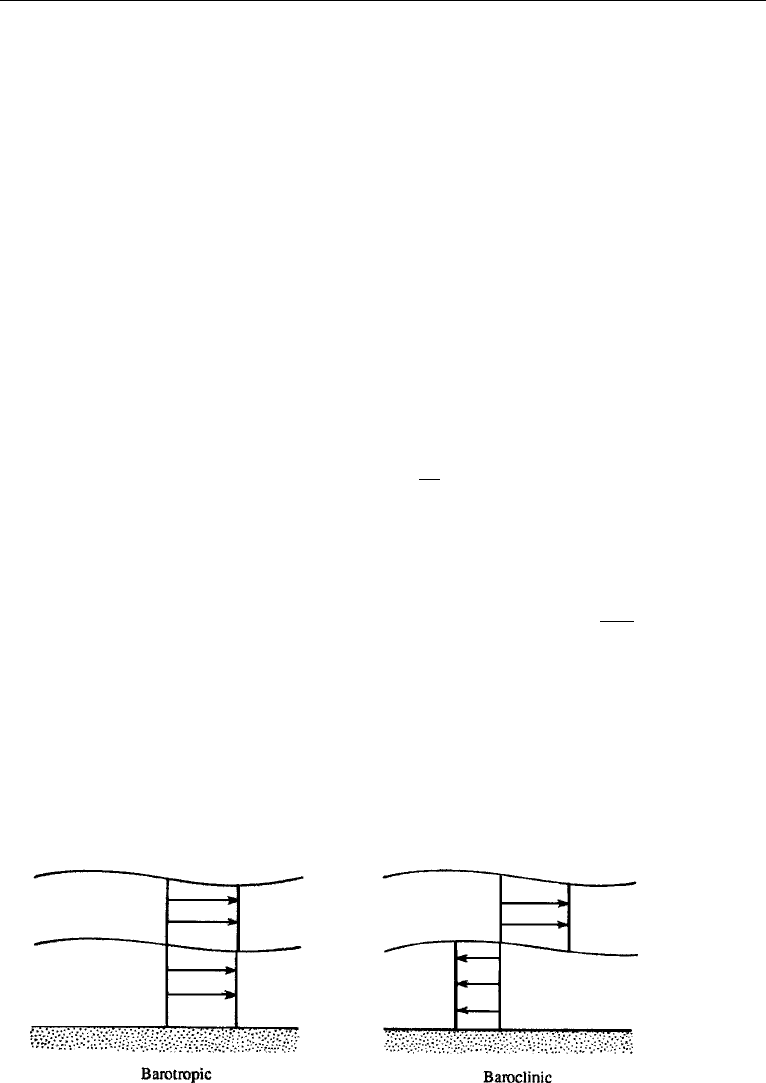
tem have a simple structure (Figure 7.31): a barotropic mode in which the horizontal

velocity is depth independent across the entire water column; and a baroclinic mode

in which the horizontal velocity is directed in opposite directions in the two layers

(but is depth independent in each layer).

We shall now summarize the results of interfacial waves presented in the pre-

ceding three sections. In the case of two inﬁnitely deep ﬂuids, only the baroclinic

mode is possible, and it has a frequency of ω = ε

√

gk. If the upper layer has ﬁnite

thickness, then both baroclinic and barotropic modes are possible. In the barotropic

mode, η and ζ are in phase, and the ﬂow decreases exponentially away from the free

surface. In the baroclinic mode, η and ζ are out of phase, the horizontal velocity

changes direction across the interface, and the motion decreases exponentially away

from the interface. If we also make the long-wave approximation for the upper layer,

then the phase speed of interfacial waves in the baroclinic mode is c =



H , the

ﬂuid velocity in the upper layer is almost horizontal and depth independent, and the

pressure in the upper layer is hydrostatic. If both layers are shallow, then the ﬂow is

depth independent and hydrostatic in both layers; the two modes in such a system

have the simple structure shown in Figure 7.31.

18. Equations of Motion for a Continuously Stratiﬁed Fluid

We have considered surface gravity waves and internal gravity waves at a density

discontinuity between two ﬂuids. Internal waves also exist if the ﬂuid is continuously

Figure 7.31 Two modes of motion in a shallow-water, two-layer system in the Boussinesq limit.

264 Gravity Waves

stratiﬁed, in which the vertical density proﬁle in a state of rest is a continuous function

¯ρ(z). The equations of motion for internal waves in such a medium will be derived

in this section, starting with the Boussinesq set (4.89) presented in Chapter 4. The

Boussinesq approximation treats density as constant, except in the vertical momentum

equation. We shall assume that the wave motion is inviscid. The amplitudes will be

assumed to be small, in which case the nonlinear terms can be neglected. We shall also

assume that the frequency of motion is much larger than the Coriolis frequency, which

therefore does not affect the motion. Effects of the earth’s rotation are considered in

Chapter 14. The set (4.89) then simpliﬁes to

∂u

∂t

=−

∂p

∂x

, (7.130)

∂v

∂t

=−

∂p

∂y

, (7.131)

∂w

∂t

=−

∂p

∂z

−

ρg

, (7.132)

Dρ

= 0, (7.133)

∂u

∂x

∂v

∂y

∂w

∂z

= 0, (7.134)

where ρ

is a constant reference density. As noted in Chapter 4, the equation

Dρ/Dt = 0isnot an expression of conservation of mass, which is expressed by

∇

•

u = 0 in the Boussinesq approximation. Rather, it expresses incompressibility

of a ﬂuid particle. If temperature is the only agency that changes the density, then

Dρ/Dt = 0 follows from the heat equation in the nondiffusive form DT /Dt = 0

and an incompressible (that is, ρ is not a function of p) equation of state in the

form δρ/ρ =−αδT, where α is the coefﬁcient of thermal expansion. If the den-

sity changes are due to changes in the concentration S of a constituent, for example

salinity in the ocean or water vapor in the atmosphere, then Dρ/Dt = 0 follows

from DS/Dt = 0 (the nondiffusive form of conservation of the constituent) and an

incompressible equation of state in the form of δρ /ρ = βδS, where β is the coefﬁ-

cient describing how the density changes due to concentration of the constituent. In

both cases, the principle underlying the equation Dρ/Dt = 0 is an incompressible

equation of state. In terms of common usage, this equation is frequently called the

“density equation,” as opposed to the continuity equation ∇

•

u = 0.

The equation set (7.130)–(7.134) consists of ﬁve equations in ﬁve unknowns

(u, v, w, p, ρ). We ﬁrst express the equations in terms of changes from a state of rest.

That is, we assume that the ﬂow is superimposed on a “background” state in which

the density ¯ρ(z) and pressure ¯p(z) are in hydrostatic balance:

0 =−

d ¯p

−

¯ρg

. (7.135)

18. Equations of Motion for a Continuously Stratiﬁed Fluid 265

When the motion develops, the pressure and density change to

p =¯p(z) + p



ρ =¯ρ(z) +ρ



(7.136)

The density equation (7.133) then becomes

∂

∂t

( ¯ρ + ρ



) + u

∂

∂x

( ¯ρ + ρ



) + v

∂

∂y

( ¯ρ + ρ



) + w

∂

∂z

( ¯ρ + ρ



) = 0. (7.137)

Here, ∂ ¯ρ/∂t = ∂ ¯ρ/∂x = ∂ ¯ρ/∂y = 0. The nonlinear terms in the second, third, and

fourth terms (namely, u∂ρ



/∂x, v∂ρ



/∂y, and w∂ρ



/∂z) are also negligible for small

amplitude motions. The linear part of the fourth term, that is, wd¯ρ/dz, represents a

very important process and must be retained. Equation (7.137) then simpliﬁes to

∂ρ



∂t

+ w

d ¯ρ

= 0, (7.138)

which states that the density perturbation at a point is generated only by the vertical

advection of the background density distribution. This is the linearized form of equa-

tion (7.133), with the vertical advection of density retained in a linearized form. We

now introduce the deﬁnition

≡−

d ¯ρ

. (7.139)

Here, N(z) has the units of frequency (rad/s) and is called the Brunt–V

ais

frequency or buoyancy frequency. It plays a fundamental role in the study of strati-

ﬁed ﬂows. We shall see in the next section that it has the signiﬁcance of being the

frequency of oscillation if a ﬂuid particle is vertically displaced.

After substitution of equation (7.136), the equations of motion (7.130)–(7.134)

become

∂u

∂t

=−

∂p



∂x

, (7.140)

∂v

∂t

=−

∂p



∂y

, (7.141)

∂w

∂t

=−

∂p



∂z

−



, (7.142)

∂ρ



∂t

−

w = 0, (7.143)

∂u

∂x

∂v

∂y

∂w

∂z

= 0. (7.144)

266 Gravity Waves

In deriving this set we have also used equation (7.135) and replaced the density

equation by its linearized form (7.138). Comparing the sets (7.130)–(7.134) and

(7.140)–(7.144), we see that the equations satisﬁed by the perturbation density and

pressure are identical to those satisﬁed by the total ρ and p.

In deriving the equations for a stratiﬁed ﬂuid, we have assumed that ρ is a

function of temperature T and concentration S of a constituent, but not of pressure.

At ﬁrst this does not seem to be a good assumption. The compressibility effects in the

atmosphere are certainly not negligible; even in the ocean the density changes due to

the huge changes in the background pressure are as much as 4%, which is ≈10 times

the density changes due to the variations of the salinity and temperature. The effects

of compressibility, however, can be handled within the Boussinesq approximation if

we regard ¯ρ in the deﬁnition of N as the background potential density, that is the

density distribution from which the adiabatic changes of density due to the changes

of pressure have been subtracted out. The concept of potential density is explained

in Chapter 1. Oceanographers account for compressibility effects by converting all

their density measurements to the standard atmospheric pressure; thus, when they

report variations in density (what they call “sigma tee”) they are generally reporting

variations due only to changes in temperature and salinity.

A useful equation for stratiﬁed ﬂows is the one involving only w. The u and v

can be eliminated by taking the time derivative of the continuity equation (7.144) and

using the horizontal momentum equations (7.140) and (7.141). This gives

∇



∂

∂z∂t

, (7.145)

where ∇

≡ ∂

/∂x

+ ∂

/∂y

is the horizontal Laplacian operator. Elimination of



from equations (7.142) and (7.143) gives

∂



∂t ∂z

=−

∂

∂t

− N

w. (7.146)

Finally, p



can be eliminated by taking ∇

of equation (7.146), and using equa-

tion (7.145). This gives

∂

∂t ∂z



∂

∂t ∂z



=−∇



∂

∂t

+ N



which can be written as

∂

∂t

∇

w + N

∇

w = 0, (7.147)

where ∇

≡ ∂

/∂x

+ ∂

/∂y

+ ∂

/∂z

=∇

+ ∂

/∂z

is the three-dimensional

Laplacian operator. The w-equation will be used in the following section to derive

the dispersion relation for internal gravity waves.

19. Internal Waves in a Continuously Stratiﬁed Fluid 267

19. Internal Waves in a Continuously Stratiﬁed Fluid

In this chapter we have considered gravity waves at the surface or at a density

discontinuity; these waves propagate only in the horizontal direction. Because every

horizontal direction is alike, such waves are isotropic, in which only the magnitude

of the wavenumber vector matters. By taking the x-axis along the direction of wave

propagation, we obtained a dispersion relation ω(k) that depends only on the mag-

nitude of the wavenumber. We found that phases and groups propagate in the same

direction, although at different speeds. If, on the other hand, the ﬂuid is continuously

stratiﬁed, then the internal waves can propagate in any direction, at any angle to the

vertical. In such a case the direction of the wavenumber vector becomes important.

Consequently, we can no longer treat the wavenumber, phase velocity, and group

velocity as scalars.

Any ﬂow variable q can now be written as

q = q

i(kx+ly+mz−ωt)

= q

i(K

•

x−ωt)

where q

is the amplitude and K = (k,l,m) is the wavenumber vector with com-

ponents k, l, and m in the three Cartesian directions. We expect that in this case the

direction of wave propagation should matter because horizontal directions are basi-

cally different from the vertical direction, along which the all-important gravity acts.

Internal waves in a continuously stratiﬁed ﬂuid are therefore anisotropic, for which

the frequency is a function of all three components of K. This can be written in the

following two ways:

ω = ω(k,l,m) = ω(K). (7.148)

However, the waves are still horizontally isotropic because the dependence of the

wave ﬁeld on k and l is similar, although the dependence on k and m is dissimilar.

The propagation of internal waves is a baroclinic process, in which the surfaces of

constant pressure do not coincide with the surfaces of constant density. It was shown

in Section 5.4, in connection with the demonstration of Kelvin’s circulation theorem,

that baroclinic processes generate vorticity. Internal waves in a continuously stratiﬁed

ﬂuid are therefore not irrotational. Waves at a density interface constitute a limiting

case in which all the vorticity is concentrated in the form of a velocity discontinuity

at the interface. The Laplace equation can therefore be used to describe the ﬂow ﬁeld

within each layer. However, internal waves in a continuously stratiﬁed ﬂuid cannot

be described by the Laplace equation.

The ﬁrst task is to derive the dispersion relation. We shall simplify the analysis

by assuming that N is depth independent, an assumption that may seem unrealistic at

ﬁrst. In the ocean, for example, N is large at a depth of ≈200 m and small elsewhere

(see Figure 14.2). Figure 14.2 shows that N<0.01 everywhere but N is largest

between ≈200 m and 2 km. However, the results obtained by treating N as constant

are locally valid if N varies slowly over the vertical wavelength 2π/m of the motion.

The so-called WKB approximation of internal waves, in which such a slow variation

of N(z) is not neglected, is discussed in Chapter 14.

268 Gravity Waves

Consider a wave propagating in three dimensions, for which the vertical veloc-

ity is

w = w

i(kx+ly+mz−ωt)

, (7.149)

where w

is the amplitude of ﬂuctuations. Substituting into the governing

equation

∂

∂t

∇

w + N

∇

w = 0, (7.147)

gives the dispersion relation

+ l

+ m

. (7.150)

For simplicity of discussion we shall orient the xz-plane so as to contain the wave-

number vector K. No generality is lost by doing this because the medium is hori-

zontally isotropic. For this choice of reference axes we have l = 0; that is, the wave

motion is two dimensional and invariant in the y-direction, and k represents the entire

horizontal wavenumber. We can then write equation (7.150) as

ω =

√

+ m

. (7.151)

This is the dispersion relation for internal gravity waves and can also be written as

ω = N cos θ, (7.152)

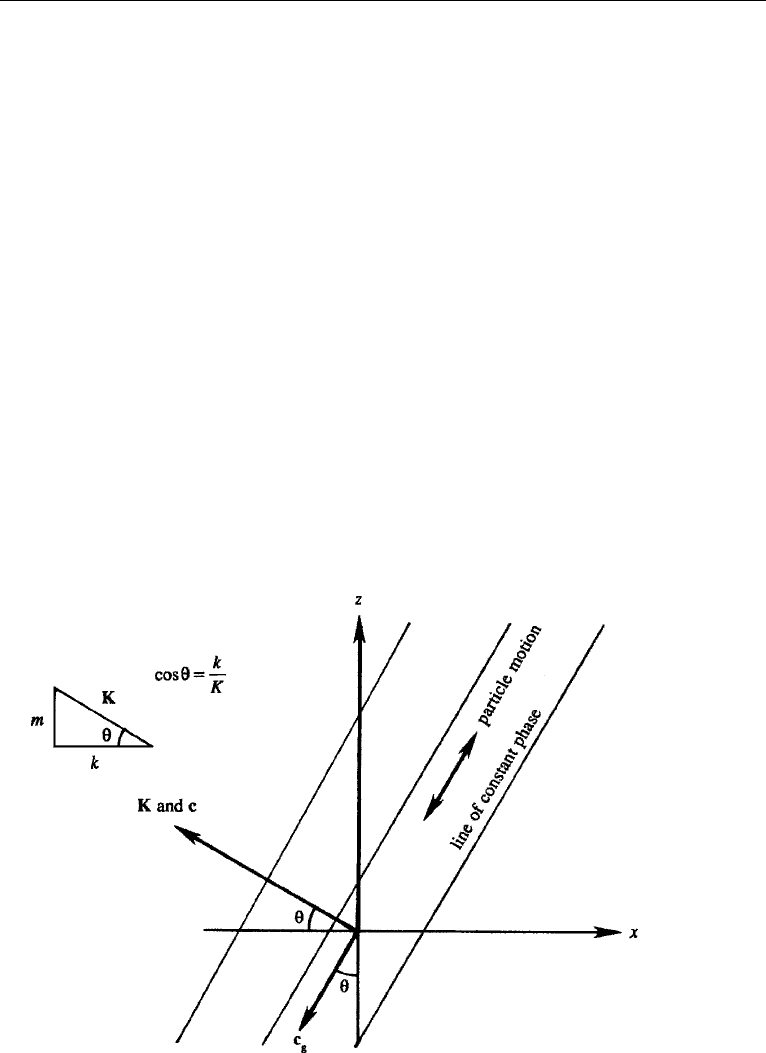
where θ is the angle between the phase velocity vector c (and therefore K) and the

horizontal direction (Figure 7.32). It follows that the frequency of an internal wave in a

stratiﬁed ﬂuid depends only on the direction of the wavenumber vector and not on the

magnitude of the wavenumber. This is in sharp contrast with surface and interfacial

gravity waves, for which frequency depends only on the magnitude. The frequency

lies in the range 0 <ω<N, revealing one important signiﬁcance of the buoyancy

frequency: N is the maximum possible frequency of internal waves in a stratiﬁed

ﬂuid.

Before discussing the dispersion relation further, let us explore particle motion

in an incompressible internal wave. The ﬂuid motion can be written as

u = u

i(kx+ly+mz−ωt)

, (7.153)

plus two similar expressions for v and w. This gives

∂u

∂x

= iku

i(kx+ly+mz−ωt)

= iku.

The continuity equation then requires that ku +lv + mw = 0, that is,

•

u = 0, (7.154)

19. Internal Waves in a Continuously Stratiﬁed Fluid 269

showing that particle motion is perpendicular to the wavenumber vector (Figure 7.32).

Note that only two conditions have been used to derive this result, namely the incom-

pressible continuity equation and a trigonometric behavior in all spatial directions. As

such, the result is valid for many other wave systems that meet these two conditions.

These waves are called shear waves (or transverse waves) because the ﬂuid moves

parallel to the constant phase lines. Surface or interfacial gravity waves do not have

this property because the ﬁeld varies exponentially in the vertical.

We can now interpret θ in the dispersion relation (7.152) as the angle between

the particle motion and the vertical direction (Figure 7.32). The maximum frequency

ω = N occurs when θ = 0, that is, when the particles move up and down vertically.

This case corresponds to m = 0 (see equation (7.151)), showing that the motion is

independent of the z-coordinate. The resulting motion consists of a series of vertical

columns, all oscillating at the buoyancy frequency N , the ﬂow ﬁeld varying in the

horizontal direction only.

The w = 0 Limit

At the opposite extreme we have ω = 0 when θ = π/2, that is, when the particle

motion is completely horizontal. In this limit our internal wave solution (7.151) would

seem to require k = 0, that is, horizontal independence of the motion. However, such

a conclusion is not valid; pure horizontal motion is not a limiting case of internal

waves, and it is necessary to examine the basic equations to draw any conclusion for

Figure 7.32 Basic parameters of internal waves. Note that c and c

are at right angles and have opposite

vertical components.

270 Gravity Waves

Figure 7.33 Blocking in strongly stratiﬁed ﬂow. The circular region represents a two-dimensional body

with its axis along the y direction.

this case. An examination of the governing set (7.140)–(7.144) shows that a possible

steady solution is w = p



= ρ



= 0, with u and v any functions of x and y satisfying

∂u

∂x

∂v

∂y

= 0. (7.155)

The z-dependence of u and v is arbitrary. The motion is therefore two-dimensional

in the horizontal plane, with the motion in the various horizontal planes decoupled

from each other. This is why clouds in the upper atmosphere seem to move in ﬂat

horizontal sheets, as often observed in airplane ﬂights (Gill, 1982). For a similar

reason a cloud pattern pierced by a mountain peak sometimes shows Karman vor-

tex streets, a two-dimensional feature; see the striking photograph in Figure 10.20.

A restriction of strong stratiﬁcation is necessary for such almost horizontal ﬂows, for

equation (7.143) suggests that the vertical motion is small if N is large.

The foregoing discussion leads to the interesting phenomenon of blocking in a

strongly stratiﬁed ﬂuid. Consider a two-dimensional body placed in such a ﬂuid, with

its axis horizontal (Figure 7.33). The two dimensionality of the body requires ∂v/∂y =

0, so that the continuity equation (7.155) reduces to ∂u/∂x = 0. A horizontal layer

of ﬂuid ahead of the body, bounded by tangents above and below it, is therefore

blocked. (For photographic evidence see Figure 3.18 in the book by Turner (1973).)

This happens because the strong stratiﬁcation suppresses the w ﬁeld and prevents the

ﬂuid from going around and over the body.

20. Dispersion of Internal Waves in a Stratiﬁed Fluid

In the case of isotropic gravity waves at a free surface and at a density discontinuity,

we found that c and c

are in the same direction, although their magnitudes can be

different. This conclusion is no longer valid for the anisotropic internal waves in a

continuously stratiﬁed ﬂuid. In fact, as we shall see shortly, they are perpendicular to

each other, violating all our intuitions acquired by observing surface gravity waves!

In three dimensions, the deﬁnition c

= dω/dk has to be generalized to

= i

∂ω

∂k

+ i

∂ω

∂l

+ i

∂ω

∂m

, (7.156)

where i

, i

are the unit vectors in the three Cartesian directions. As in the preceding

section, we orient the xz-plane so that the wavenumber vector K lies in this plane

20. Dispersion of Internal Waves in a Stratiﬁed Fluid 271

and l = 0. Substituting equation (7.151), this gives

m − i

k). (7.157)

The phase velocity is

c =

k + i

m), (7.158)

where K/K represents the unit vector in the direction of K. (Note that c = i

(ω/k)+

(ω/m), as explained in Section 3.) It follows from equations (7.157) and (7.158)

that

•

c = 0, (7.159)

showing that phase and group velocity vectors are perpendicular.

Equations (7.157) and (7.158) show that the horizontal components of c and c

are in the same direction, while their vertical components are equal and opposite. In

fact, c and c

form two sides of a right-angled triangle whose hypotenuse is horizontal

(Figure 7.34). Consequently, the phase velocity has an upward component when the

group velocity has a downward component, and vice versa. Equations (7.154) and

(7.159) are consistent because c and K are parallel and c

and u are parallel. The fact

that c and c

are perpendicular, and have opposite vertical components, is illustrated in

Figure 7.35. It shows that the phase lines are propagating toward the left and upward,

whereas the wave groups are propagating to the left and downward. Wave crests are

constantly appearing at one edge of the group, propagating through the group, and

vanishing at the other edge.

The group velocity here has the usual signiﬁcance of being the velocity of prop-

agation of energy of a certain sinusoidal component. Suppose a source is oscillating

at frequency ω. Then its energy will only be found radially outward along four beams

oriented at an angle θ with the vertical, where cos θ = ω/N. This has been veriﬁed

in a laboratory experiment (Figure 7.36). The source in this case was a vertically

oscillating cylinder with its axis perpendicular to the plane of paper. The frequency

was ω<N. The light and dark lines in the photograph are lines of constant density,

made visible by an optical technique. The experiment showed that the energy radiated

Figure 7.34 Orientation of phase and group velocity in internal waves.