Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

242 Gravity Waves

10. Group Velocity and Wave Dispersion

Physical Motivation

We continue our discussion of group velocity in this section, focussing on how the

different wavelength and frequency components are propagated. Consider waves in

deep water, for which

c =



gλ

2π

signifying that larger waves propagate faster. Suppose that a surface disturbance is

generated by dropping a stone into a pool. The initial disturbance can be thought of

as being composed of a great many wavelengths. A short time later, at t = t

, the sea

surface may have the rather irregular proﬁle shown in Figure 7.19. The appearance

of the surface at a later time t

, however, is more regular, with the longer components

(which have been traveling faster) out in front. The waves in front are the longest

waves produced by the initial disturbance; we denote their length by λ

max

, typically

a few times larger than the stone. The leading edge of the wave system therefore

propagates at the group speed corresponding to these wavelengths, that is, at the

speed

g max



gλ

max

2π

(Pure capillary waves can propagate faster than this speed, but they have small mag-

nitude and get dissipated rather soon.) The region of initial disturbance becomes calm

because there is a minimum group velocity of gravity waves due to the inﬂuence of

surface tension, namely 17.8 cm/s (Exercise 4). The trailing edge of the wave system

therefore travels at speed

g min

= 17.8cm/s.

With c

g max

> 17.8cm/s for ordinary sizes of stones, the length of the disturbed region

gets larger, as shown in Figure 7.19. The wave heights are correspondingly smaller

because there is a ﬁxed amount of energy in the wave system. (Wave dispersion,

therefore, makes the linearity assumption more accurate.) The smoothening of the

proﬁle and the spreading of the region of disturbance continue until the amplitudes

become imperceptible or the waves are damped by viscous dissipation. It is clear

that the initial superposition of various wavelengths, running for some time, will sort

themselves out in the sense that the different sinusoidal components, differing widely

in their wavenumbers, become spatially separated, and are found in quite different

places. This is a basic feature of the behavior of a dispersive system.

The wave group as a whole travels slower than the individual crests. Therefore,

if we try to follow the last crest at the rear of the train, quite soon we ﬁnd that it is the

second one from the rear; a new crest has been born behind it. In fact, new crests are

constantly “popping up from nowhere” at the rear of the train, propagating through

the train, and ﬁnally disappearing in front of the train. This is because, by following a

particular crest, we are traveling at twice the speed at which the energy of waves of a

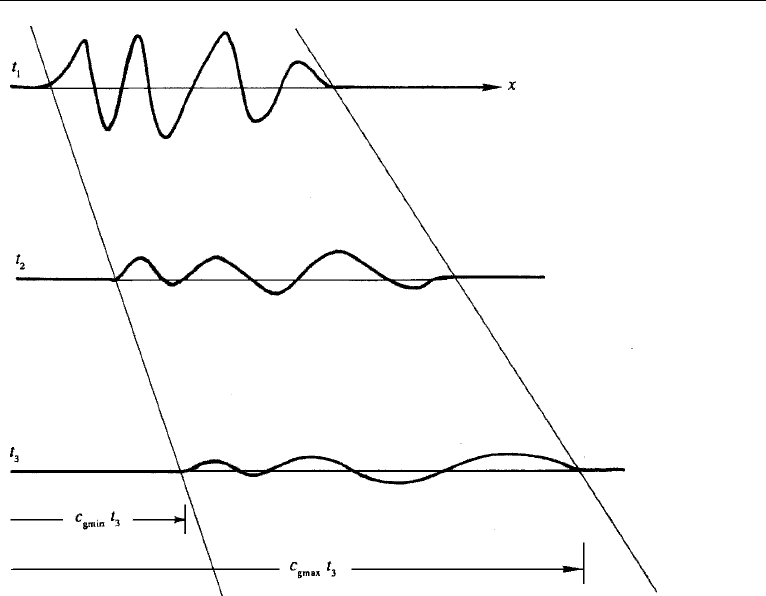
10. Group Velocity and Wave Dispersion 243

Figure 7.19 Surface proﬁles at three values of time due to a disturbance caused by dropping a stone into

a pool.

particular length is traveling. Consequently, we do not see a wave of ﬁxed wavelength

if we follow a particular crest. In fact, an individual wave constantly becomes longer

as it propagates through the train. When its length becomes equal to the longest wave

generated initially, it cannot evolve any more and dies out. Clearly, the waves in front

of the train are the longest Fourier components present in the initial disturbance.

Layer of Constant Depth

We shall now prove that an observer traveling at c

would see no change in k if the

layer depth H is uniform everywhere. Consider a wavetrain of “gradually varying

wavelength,” such as the one shown at later time values in Figure 7.19. By this we

mean that the distance between successive crests varies slowly in space and time.

Locally, we can describe the free surface displacement by

η = a(x, t) cos[θ(x,t)], (7.80)

where a(x, t) is a slowly varying amplitude and θ(x,t) is the local phase. We know

that the phase angle for a wavenumber k and frequency ω is θ = kx − ωt. For a

gradually varying wavetrain, we can deﬁne a local wavenumber k(x, t) and a local

244 Gravity Waves

frequency ω(x,t) as the rate of change of phase in space and time, respectively.

That is,

k =

∂θ

∂x

ω =−

∂θ

∂t

(7.81)

Cross differentiation gives

∂k

∂t

∂ω

∂x

= 0. (7.82)

Now suppose we have a dispersion relation relating ω solely to k in the form

ω = ω(k). We can then write

∂ω

∂x

dω

∂k

∂x

so that equation (7.82) becomes

∂k

∂t

+ c

∂k

∂x

= 0, (7.83)

where c

= dω/dk. The left-hand side of equation (7.83) is similar to the material

derivative and gives the rate of change of k as seen by an observer traveling at speed

. Such an observer will always see the same wavelength. Group velocity is therefore

the speed at which wavenumbers are advected. This is shown in the xt-diagram of

Figure 7.20, where wave crests are followed along lines dx/dt = c and wavelengths

are preserved along the lines dx/dt = c

. Note that the width of the disturbed region,

bounded by the ﬁrst and last thick lines in Figure 7.20, increases with time, and that

the crests constantly appear at the back of the group and vanish at the front.

Layer of Variable Depth H(x)

The conclusion that an observer traveling at c

sees only waves of the same length is

true only for waves in a homogeneous medium, that is, a medium whose properties

are uniform everywhere. In contrast, a sea of nonuniform depth H(x)behaves like an

inhomogeneous medium, provided the waves are shallow enough to feel the bottom.

In such a case it is the frequency of the wave, and not its wavelength, that remains

constant along the path of propagation of energy. To demonstrate this, consider a case

where H(x) is gradually varying (on the scale of a wavelength) so that we can still

use the dispersion relation (7.40) with H replaced by H(x):

ω =



gk tanh[kH (x)].

Such a dispersion relation has a form

ω = ω(k,x). (7.84)

10. Group Velocity and Wave Dispersion 245

In such a case we can ﬁnd the group velocity at a point as

(k, x) =

∂ω(k, x)

∂k

, (7.85)

which on multiplication by ∂k/∂t gives

∂k

∂t

∂ω

∂k

∂t

∂ω

∂t

. (7.86)

Multiplying equation (7.82) by c

and using equation (7.86) we obtain

∂ω

∂t

+ c

∂ω

∂x

= 0. (7.87)

In three dimensions, this is written as

∂ω

∂t

+ c

•

∇ω = 0,

which shows that ω remains constant to an observer traveling with the group velocity

in an inhomogeneous medium.

Summarizing, an observer traveling at c

in a homogeneous medium sees constant

values of k, ω(k), c, and c

(k). Consequently, ray paths describing group velocity in

the xt-plane are straight lines (Figure 7.20). In an inhomogeneous medium only ω

Figure 7.20 Propagation of a wave group in a homogeneous medium, represented on an xt-plot. Thin

lines indicate paths taken by wave crests, and thick lines represent paths along which k and ω are con-

stant. M. J. Lighthill, Waves in Fluids, 1978 and reprinted with the permission of Cambridge University

Press, London.

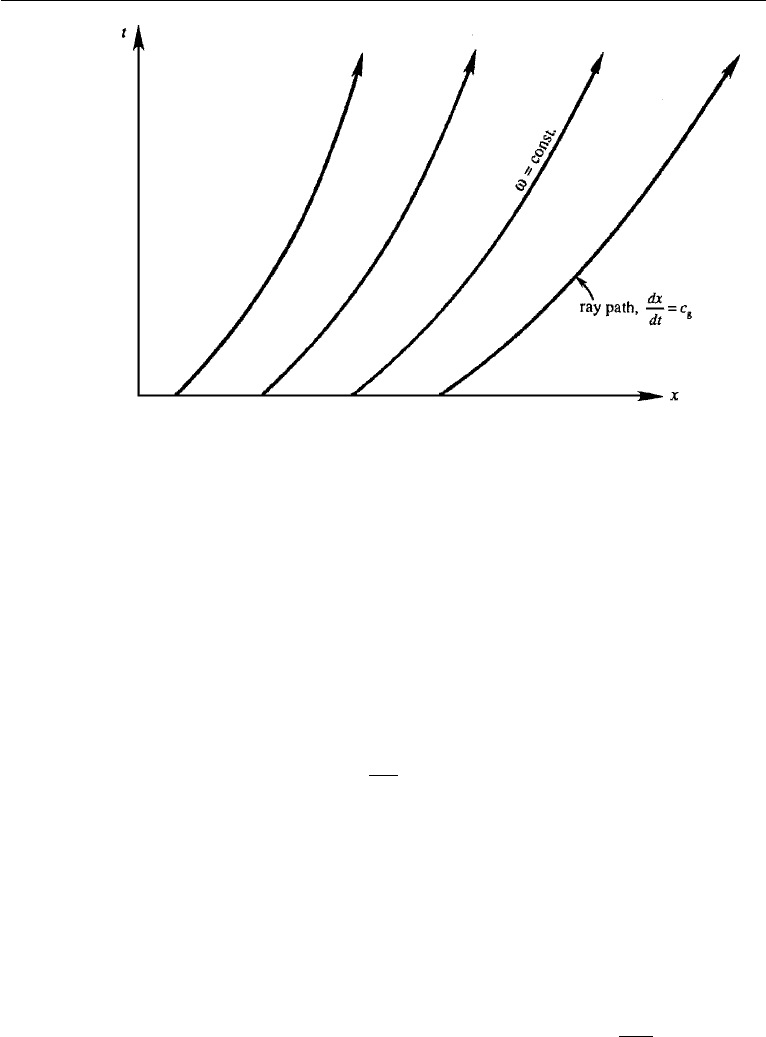
246 Gravity Waves

Figure 7.21 Propagation of a wave group in an inhomogeneous medium represented on an xt-plot. Only

ray paths along which ω is constant are shown. M. J. Lighthill, Waves in Fluids, 1978 and reprinted with

the permission of Cambridge University Press, London.

remains constant along the lines dx/dt = c

,butk, c, and c

can change. Conse-

quently, ray paths are not straight in this case (Figure 7.21).

11. Nonlinear Steepening in a Nondispersive Medium

Until now we have assumed that the wave amplitude is small. This has enabled us to

neglect the higher-order terms in the Bernoulli equation and to apply the boundary

conditions at z = 0 instead of at the free surface z = η. One consequence of such

linear analysis has been that waves of arbitrary shape propagate unchanged in form

if the system is nondispersive, such as shallow water waves. The unchanging form is

a result of the fact that all wavelengths, of which the initial waveform is composed,

propagate at the same speed c =

√

gH, provided all the sinusoidal components satisfy

the shallow-water approximation Hk  1. We shall now see that the unchanging

waveform result is no longer valid if ﬁnite amplitude effects are considered. Several

other nonlinear effects will also be discussed in the following sections.

Finite amplitude effects can be formally treated by the method of characteristics;

this is discussed, for example, in Liepmann and Roshko (1957) and Lighthill (1978).

Instead, we shall adopt only a qualitative approach here. Consider a ﬁnite amplitude

surface displacement consisting of an elevation and a depression, propagating in

shallow-water of undisturbed depth H (Figure 7.22). Let a little wavelet be superposed

on the elevation at point x, at which the water depth is H



(x) and the ﬂuid velocity

due to the wave motion is u(x). Relative to an observer moving with the ﬂuid velocity

u, the wavelet propagates at the local shallow-water speed c



. The speed of

the wavelet relative to a frame of reference ﬁxed in the undisturbed ﬂuid is therefore

c = c



+ u. It is apparent that the local wave speed c is no longer constant because

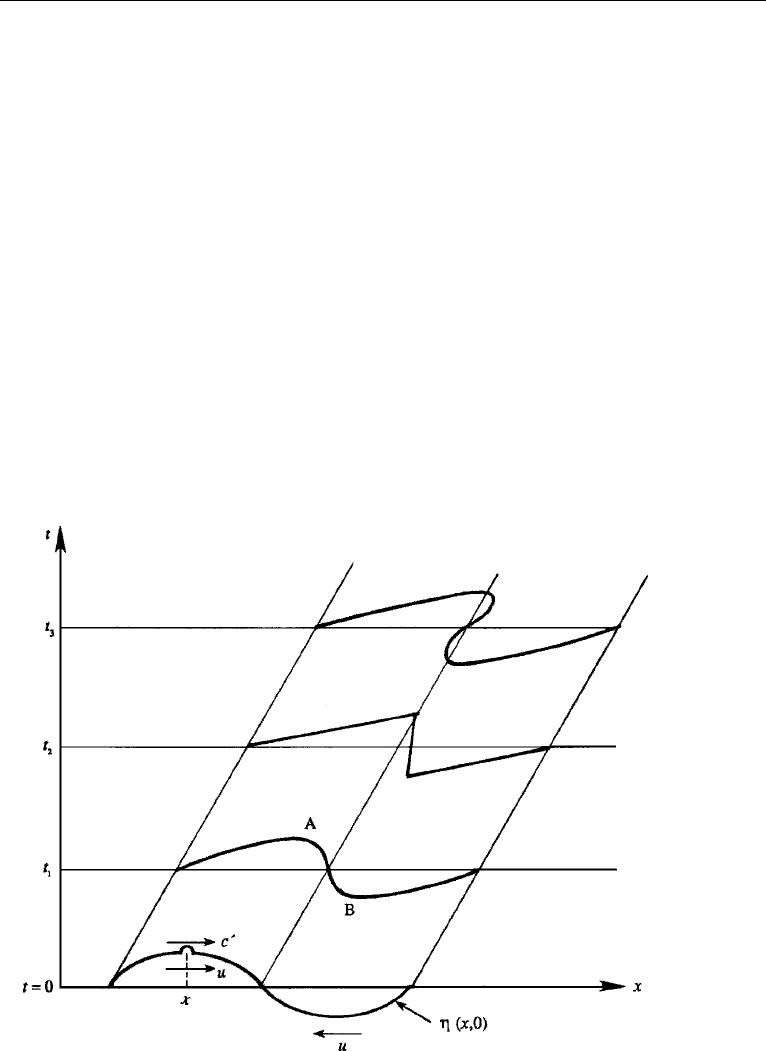
11. Nonlinear Steepening in a Nondispersive Medium 247



(x) and u(x) are variables. This is in contrast to the linearized theory in which u is

negligible and c



is constant because H



 H .

Let us now examine the effect of such a variable c on the wave proﬁle. The value

of c



is larger for points on the elevation than for points on the depression. From

Figure 7.7 we also know that the ﬂuid velocity u is positive (that is, in the direction

of wave propagation) under an elevation and negative under a depression. It follows

that wave speed c is larger for points on the hump than for points on the depression,

so that the waveform undergoes a “shearing deformation” as it propagates, the region

of elevation tending to overtake the region of depression (Figure 7.22).

We shall call the front face AB a “compression region” because the elevation here

is rising with time. Figure 7.22 shows that the net effect of nonlinearity is a steepening

of the compression region. For ﬁnite amplitude waves in a nondispersive medium

like shallow water, therefore, there is an important distinction between compression

and expansion regions. A compression region tends to steepen with time and form

a jump, while an expansion region tends to ﬂatten out. This eventually would lead

to the shape shown at the top of Figure 7.22, implying the physically impossible

situation of three values of surface elevation at a point. However, before this happens

the wave slope becomes nearly inﬁnite (proﬁle at t

in Figure 7.22), so that dissipative

Figure 7.22 Wave proﬁles at four values of time. At t

the proﬁle has formed a hydraulic jump. The

proﬁle at t

is impossible.

248 Gravity Waves

processes including wave breaking and foaming become important, and the previous

inviscid arguments become inapplicable. Such a waveform has the form of a front

and propagates into still ﬂuid at constant speed that lies between

√

and

√

where H

and H

are the water depths on the two sides of the front. This is called

the hydraulic jump, which is similar to the shock wave in a compressible ﬂow. This

is discussed further in the following section.

12. Hydraulic Jump

In the previous section we saw how steepening of the compression region of a surface

wave in shallow water leads to the formation of a jump, which subsequently propagates

into the undisturbed ﬂuid at constant speed and without further change in form. In

this section we shall discuss certain characteristics of ﬂow across such a jump. Before

we do so, we shall introduce certain deﬁnitions.

Consider the ﬂow in a shallow canal of depth H . If the ﬂow speed is u,wemay

deﬁne a nondimensional speed by

Fr ≡

√

This is called the Froude number, which is the ratio of the speed of ﬂow to the speed of

inﬁnitesimal gravity waves. The ﬂow is called supercritical if Fr > 1, and subcritical

if Fr < 1. The Froude number is analogous to the Mach number in compressible ﬂow,

deﬁned as the ratio of the speed of ﬂow to the speed of sound in the medium.

It was seen in the preceding section that a hydraulic jump propagates into a

still ﬂuid at a speed (say, u

) that lies between the long-wave speeds on the two

sides, namely, c

√

and c

√

(Figure 7.23c). Now suppose a leftward

propagating jump is made stationary by superposing a ﬂow u

directed to the right.

In this frame the ﬂuid enters the jump at speed u

and exits at speed u

(Figure 7.23b). Because c

, it follows that Fr

> 1 and Fr

< 1. Just as

a compressible ﬂow suddenly changes from a supersonic to subsonic state by going

through a shock wave (Section 16.6), a supercritical ﬂow in a shallow canal can change

into a subcritical state by going through a hydraulic jump. The depth of ﬂow rises

downstream of a hydraulic jump, just as the pressure rises downstream of a shock

wave. To continue the analogy, mechanical energy is lost by dissipative processes

both within the hydraulic jump and within the shock wave. A common example of

a stationary hydraulic jump is found at the foot of a dam, where the ﬂow almost

always reaches a supercritical state because of the free fall (Figure 7.23a). A tidal

bore propagating into a river mouth is an example of a propagating hydraulic jump.

Consider a control volume across a stationary hydraulic jump shown in Figure

7.23b. The depth rises from H

to H

and the velocity falls from u

to u

.IfQ is

the volume rate of ﬂow per unit width normal to the plane of the paper, then mass

conservation requires

Q = u

= u

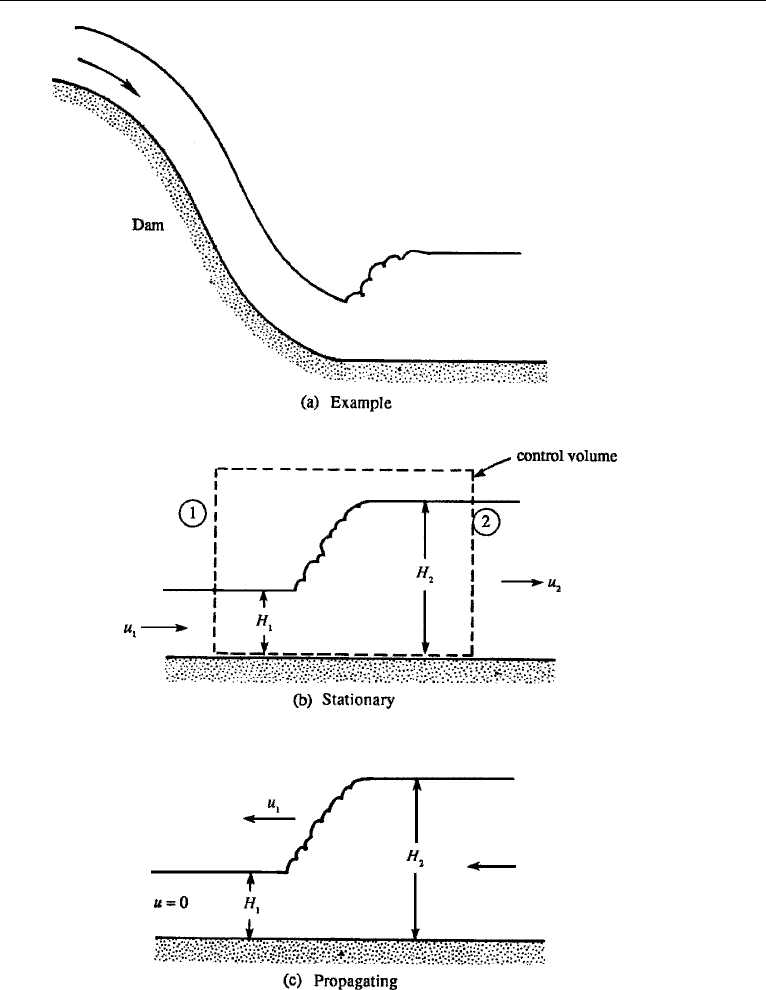
12. Hydraulic Jump 249

Figure 7.23 Hydraulic jump.

250 Gravity Waves

Now use the momentum principle (Section 4.8), which says that the sum of the

forces on a control volume equals the momentum outﬂow rate at section 2 minus the

momentum inﬂow rate at section 1. The force at section 1 is the average pressure

ρgH

/2 times the area H

; similarly, the force at section 2 is ρgH

/2. If the distance

between sections 1 and 2 is small, then the force exerted by the bottom wall of the

canal is negligible. Then the momentum theorem gives

ρgH

−

ρgH

= ρQ(u

− u

Substituting u

= Q/H

and u

= Q/H

on the right-hand side, we obtain

− H

) = Q



−



. (7.88)

Canceling the factor (H

− H

), we obtain





− 2Fr

= 0,

where Fr

= Q

/gH

= u

/gH

. The solution is

(−1 +



1 + 8Fr

). (7.89)

For supercritical ﬂows Fr

> 1, for which equation (7.89) shows that H

. There-

fore, depth of water increases downstream of the hydraulic jump.

Although the solution H

for Fr

< 1 is allowed by equation (7.89), such

a solution violates the second law of thermodynamics, because it implies an increase

of mechanical energy of the ﬂow. To see this, consider the mechanical energy of a

ﬂuid particle at the surface, E = u

/2 +gH = Q

/2H

+ gH . Eliminating Q by

equation (7.88) we obtain, after some algebra,

− E

=−(H

− H

)

g(H

− H

)

This shows that H

implies E

, which violates the second law of ther-

modynamics. The mechanical energy, in fact, decreases in a hydraulic jump because

of the eddying motion within the jump.

A hydraulic jump not only appears at the free surface, but also at density interfaces

in a stratiﬁed ﬂuid, in the laboratory as well as in the atmosphere and the ocean. (For

example, see Turner (1973), Figure 3.11, for his photograph of an internal hydraulic

jump on the lee side of a mountain.)

13. Finite Amplitude Waves of Unchanging Form in a

Dispersive Medium

In Section 11 we considered a nondispersive medium, and found that nonlinear

effects continually accumulate and add up until they become large changes. Such an

13. Finite Amplitude Waves of Unchanging Form in a Dispersive Medium 251

accumulation is prevented in a dispersive medium because the different Fourier com-

ponents propagate at different speeds and become separated from each other. In a

dispersive system, then, nonlinear steepening could cancel out the dispersive spread-

ing, resulting in ﬁnite amplitude waves of constant form. This is indeed the case. A

brief description of the phenomenon is given here; further discussion can be found in

Lighthill (1978), Whitham (1974), and LeBlond and Mysak (1978).

Note that if the amplitude is negligible, then in a dispersive system a wave of

unchanging form can only be perfectly sinusoidal because the presence of any other

Fourier component would cause the sinusoids to propagate at different speeds, result-

ing in a change in the wave shape.

Finite Amplitude Waves in Deep Water: The Stokes Wave

In 1847 Stokes showed that periodic waves of ﬁnite amplitude are possible in deep

water. In terms of a power series in the amplitude a, he showed that the surface

elevation of irrotational waves in deep water is given by

η = a cos k(x − ct) +

cos 2k(x − ct)

cos 3k(x − ct) +···, (7.90)

where the speed of propagation is

c =



(1 + k

). (7.91)

Equation (7.90) is the Fourier series for the waveform η. The addition of Fourier

components of different wavelengths in equation (7.90) shows that the wave proﬁle

η is no longer exactly sinusoidal. The arguments in the cosine terms show that all the

Fourier components propagate at the same speed c, so that the wave proﬁle propa-

gates unchanged in time. It has now been established that the existence of periodic

wavetrains of unchanging form is a typical feature of nonlinear dispersive systems.

Another important result, generally valid for nonlinear systems, is that the wave speed

depends on the amplitude, as in equation (7.91).

Periodic ﬁnite-amplitude irrotational waves in deep water are frequently called

Stokes’ waves. They have a ﬂattened trough and a peaked crest (Figure 7.24). The

maximum possible amplitude is a

max

= 0.07λ, at which point the crest becomes

a sharp 120

◦

angle. Attempts at generating waves of larger amplitude result in the

appearance of foam (white caps) at these sharp crests. In ﬁnite amplitude waves, ﬂuid

particles no longer trace closed orbits, but undergo a slow drift in the direction of

wave propagation; this is discussed in Section 14.

Figure 7.24 The Stokes wave. It is a ﬁnite amplitude periodic irrotational wave in deep water.