Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

222 Gravity Waves

In order to apply the boundary conditions, we need to assume a form for η(x, t). The

simplest case is that of a sinusoidal component with wavenumber k and frequency ω,

for which

η = a cos(kx − ωt). (7.33)

One motivation for studying sinusoidal waves is that small-amplitude waves on a water

surface become roughly sinusoidal some time after their generation (unless the water

depth is very shallow). This is due to the phenomenon of wave dispersion discussed

in Section 10. A second, and stronger, motivation is that an arbitrary disturbance

can be decomposed into various sinusoidal components by Fourier analysis, and the

response of the system to an arbitrary small disturbance is the sum of the responses

to the various sinusoidal components.

For a cosine dependence of η on (kx − ωt), conditions (7.27) and (7.32) show

that φ must be a sine function of (kx − ωt). Consequently, we assume a separable

solution of the Laplace equation in the form

φ = f(z)sin(kx − ωt), (7.34)

where f(z) and ω(k) are to be determined. Substitution of equation (7.34) into the

Laplace equation (7.22) gives

− k

f = 0,

whose general solution is

f(z) = Ae

+ Be

−kz

The velocity potential is then

φ = (Ae

+ Be

−kz

) sin(kx − ωt). (7.35)

The constants A and B are now determined from the boundary conditions (7.24) and

(7.27). Condition (7.24) gives

B = Ae

−2kH

. (7.36)

Before applying condition (7.27) in the linearized form, let us explore what would

happen if we applied it at z = η. From (7.35) we get

∂φ

∂z



z=η

= k(Ae

kη

− Be

−kη

) sin(kx − ωt),

Here we can set e

kη

 e

−kη

 1ifkη  1, valid for small slope of the free surface.

This is effectively what we are doing by applying the surface boundary conditions

equations (7.27) and (7.32) at z = 0 (instead of at z = η), which we justiﬁed

previously by a Taylor series expansion.

Substitution of equations (7.33) and (7.35) into the surface velocity condition

(7.27) gives

k(A −B) = aω. (7.37)

5. Some Features of Surface Gravity Waves 223

The constants A and B can now be determined from equations (7.36) and (7.37) as

A =

aω

k(1 −e

−2kH

)

B =

aω e

−2kH

k(1 −e

−2kH

)

The velocity potential (7.35) then becomes

φ =

aω

cosh k(z + H)

sinh kH

sin(kx − ωt), (7.38)

from which the velocity components are found as

u = aω

cosh k(z + H)

sinh kH

cos(kx − ωt),

w = aω

sinh k(z + H)

sinh kH

sin(kx − ωt).

(7.39)

We have solved the Laplace equation using kinematic boundary conditions alone.

This is typical of irrotational ﬂows. In the last chapter we saw that the equation of

motion, or its integral, the Bernoulli equation, is brought into play only to ﬁnd the

pressure distribution, after the problem has been solved from kinematic considerations

alone. In the present case, we shall ﬁnd that application of the dynamic free surface

condition (7.32) gives a relation between k and ω.

Substitution of equations (7.33) and (7.38) into (7.32) gives the desired relation

ω =



gk tanh kH, (7.40)

The phase speed c = ω/k is related to the wave size by

c =



tanh kH =



gλ

2π

tanh

2πH

(7.41)

This shows that the speed of propagation of a wave component depends on its

wavenumber. Waves for which c is a function of k are called dispersive because

waves of different lengths, propagating at different speeds, “disperse” or separate.

(Dispersion is a word borrowed from optics, where it signiﬁes separation of different

colors due to the speed of light in a medium depending on the wavelength.) A relation

such as equation (7.40), giving ω as a function of k, is called a dispersion relation

because it expresses the nature of the dispersive process. Wave dispersion is a fun-

damental process in many physical phenomena; its implications in gravity waves are

discussed in Sections 9 and 10.

5. Some Features of Surface Gravity Waves

Several features of surface gravity waves are discussed in this section. In particular, we

shall examine the nature of pressure change, particle motion, and the energy ﬂow due

to a sinusoidal propagating wave. The water depth H is arbitrary; simpliﬁcations that

result from assuming the depth to be shallow or deep are discussed in the next section.

224 Gravity Waves

Pressure Change Due to Wave Motion

It is sometimes possible to measure wave parameters by placing pressure sensors at

the bottom or at some other suitable depth. One would therefore like to know how deep

the pressure ﬂuctuations penetrate into the water. Pressure is given by the linearized

Bernoulli equation

∂φ

∂t

+ gz = 0.

If we deﬁne



≡ p + ρgz, (7.42)

as the perturbation pressure, that is, the pressure change from the undisturbed pressure

of −ρgz, then Bernoulli’s equation gives



=−ρ

∂φ

∂t

. (7.43)

On substituting equation (7.38), we obtain



ρaω

cosh k(z + H)

sinh kH

cos(kx − ωt), (7.44a)

which, on using the dispersion relation (7.40), becomes



= ρga

cosh k(z + H)

cosh kH

cos(kx − ωt). (7.44b)

The perturbation pressure therefore decays into the water column, and whether it

could be detected by a sensor depends on the magnitude of the water depth in relation

to the wavelength. This is discussed further in Section 6.

Particle Path and Streamline

To examine particle orbits, we obviously need to use Lagrangian coordinates. (See

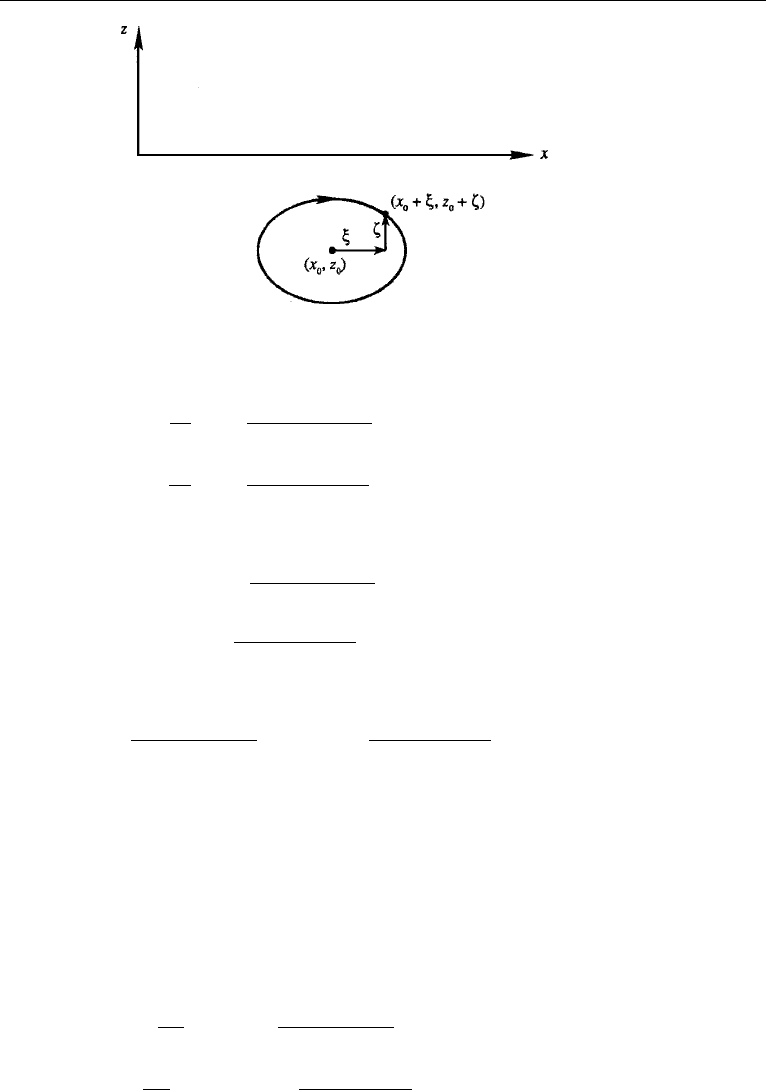
Chapter 3, Section 2 for a discussion of the Lagrangian description.) Let (x

+ξ,z

+ζ )

be the coordinates of a ﬂuid particle whose rest position is (x

), as shown in Fig-

ure 7.5. We can use (x

) as a “tag” for particle identiﬁcation, and write ξ(x

,t)

and ζ(x

,t)in the Lagrangian form. Then the velocity components are given by

u =

∂ξ

∂t

w =

∂ζ

∂t

(7.45)

where the partial derivative symbol is used because the particle identity (x

)is

kept ﬁxed in the time derivatives. For small-amplitude waves, the particle excursion

(ξ,ζ) is small, and the velocity of a particle along its path is nearly equal to the

ﬂuid velocity at the mean position (x

) at that instant, given by equation (7.39).

5. Some Features of Surface Gravity Waves 225

Figure 7.5 Orbit of a ﬂuid particle whose mean position is (x

Therefore, equation (7.45) gives

∂ξ

∂t

= aω

cosh k(z

+ H)

sinh kH

cos(kx

− ωt),

∂ζ

∂t

= aω

sinh k(z

+ H)

sinh kH

sin(kx

− ωt).

Integrating in time, we obtain

ξ =−a

cosh k(z

+ H)

sinh kH

sin(kx

− ωt),

ζ = a

sinh k(z

+ H)

sinh kH

cos(kx

− ωt).

(7.46)

Elimination of (kx

− ωt)gives



cosh k(z

+ H)

sinh kH



+ ζ



sinh k(z

+ H)

sinh kH



= 1, (7.47)

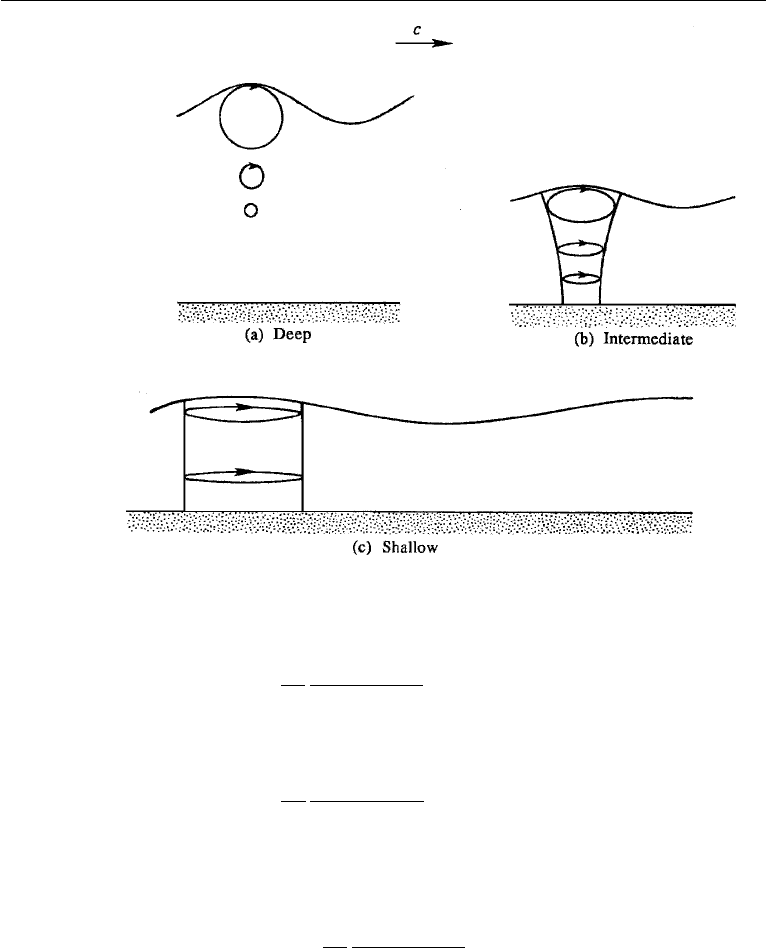
which represents ellipses. Both the semimajor axis, a cosh[k(z

+H)]/sinh kH and

the semiminor axis, a sinh[k(z

+ H)]/sinh kH decrease with depth, the minor axis

vanishing at z

=−H (Figure 7.6b). The distance between foci remains constant

with depth. Equation (7.46) shows that the phase of the motion (that is, the argument

of the sinusoidal term) is independent of z

. Fluid particles in any vertical column are

therefore in phase. That is, if one of them is at the top of its orbit, then all particles at

the same x

are at the top of their orbits.

To ﬁnd the streamline pattern, we need to determine the streamfunction ψ, related

to the velocity components by

∂ψ

∂z

= u = aω

cosh k(z + H)

sinh kH

cos(kx − ωt), (7.48)

∂ψ

∂x

=−w =−aω

sinh k(z + H)

sinh kH

sin(kx − ωt), (7.49)

226 Gravity Waves

Figure 7.6 Particle orbits of wave motion in deep, intermediate and shallow seas.

where equation (7.39) has been introduced. Integrating equation (7.48) with respect

to z, we obtain

ψ =

aω

sinh k(z + H)

sinh kH

cos(kx − ωt) + F(x,t),

where F(x,t) is an arbitrary function of integration. Similarly, integration of equa-

tion (7.49) with respect to x gives

ψ =

aω

sinh k(z + H)

sinh kH

cos(kx − ωt) + G(z, t),

where G(z, t) is another arbitrary function. Equating the two expressions for ψ we

see that F = G = function of time only; this can be set to zero if we regard ψ as due

to wave motion only, so that ψ = 0 when a = 0. Therefore

ψ =

aω

sinh k(z + H)

sinh kH

cos(kx − ωt). (7.50)

Let us examine the streamline structure at a particular time, say, t = 0, when

ψ ∝ sinh k(z + H)cos kx.

It is clear that ψ = 0atz =−H , so that the bottom wall is a part of the ψ = 0

streamline. However, ψ is also zero at kx =±π/2, ±3π/2,... for any z. At these

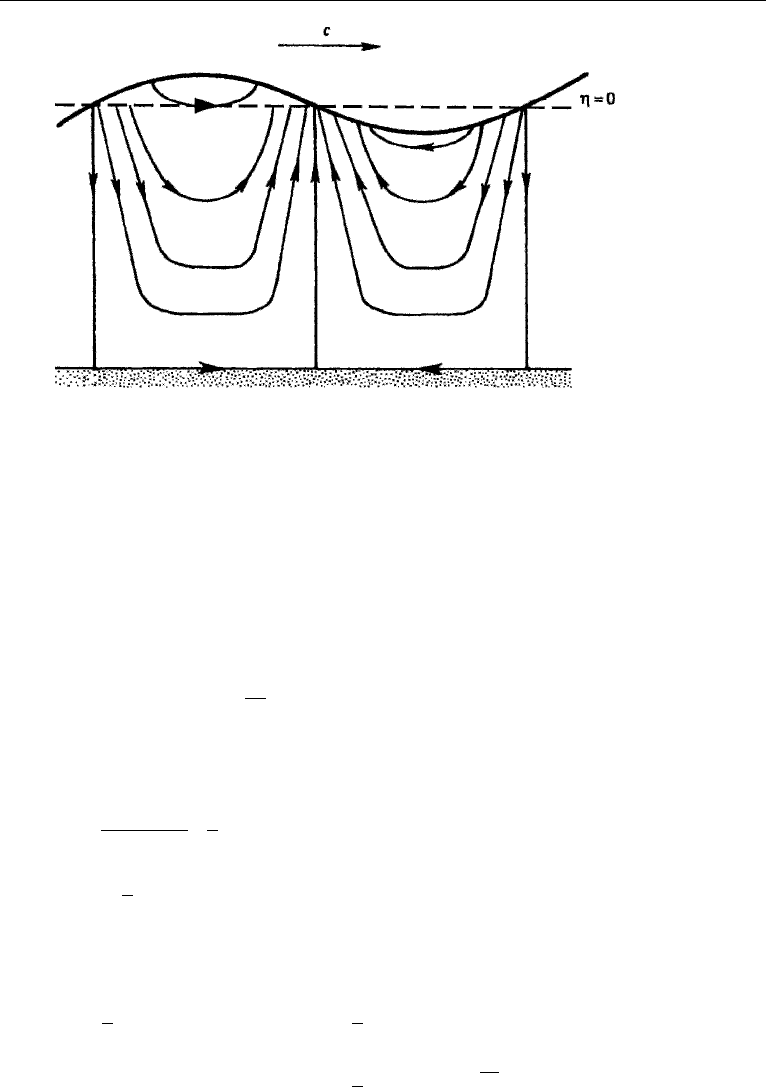
5. Some Features of Surface Gravity Waves 227

Figure 7.7 Instantaneous streamline pattern in a surface gravity wave propagating to the right.

values of kx, equation (7.33) shows that η vanishes. The resulting streamline pattern

is shown in Figure 7.7. It is seen that the velocity is in the direction of propagation

(and horizontal ) at all depths below the crests, and opposite to the direction of

propagation at all depths below troughs.

Energy Considerations

Surface gravity waves possess kinetic energy due to motion of the ﬂuid and potential

energy due to deformation of the free surface. Kinetic energy per unit horizontal area

is found by integrating over the depth and averaging over a wavelength:

2λ



−H

+ w

)dzdx.

Here the z-integral is taken up to z = 0, because the integral up to z = η gives a

higher-order term. Substitution of the velocity components from equation (7.39) gives

ρω

2 sinh





cos

(kx − ωt) dx



−H

cosh

k(z + H)dz



sin

(kx − ωt) dx



−H

sinh

k(z + H)dz



. (7.51)

In terms of free surface displacement η, the x-integrals in equation (7.51) can be

written as



cos

(kx − ωt) dx =



sin

(kx − ωt) dx



dx = η

228 Gravity Waves

where η

is the mean square displacement. The z-integrals in equation (7.51) are easy

to evaluate by expressing the hyperbolic functions in terms of exponentials. Using

the dispersion relation (7.40), equation (7.51) ﬁnally becomes

ρgη

, (7.52)

which is the kinetic energy of the wave motion per unit horizontal area.

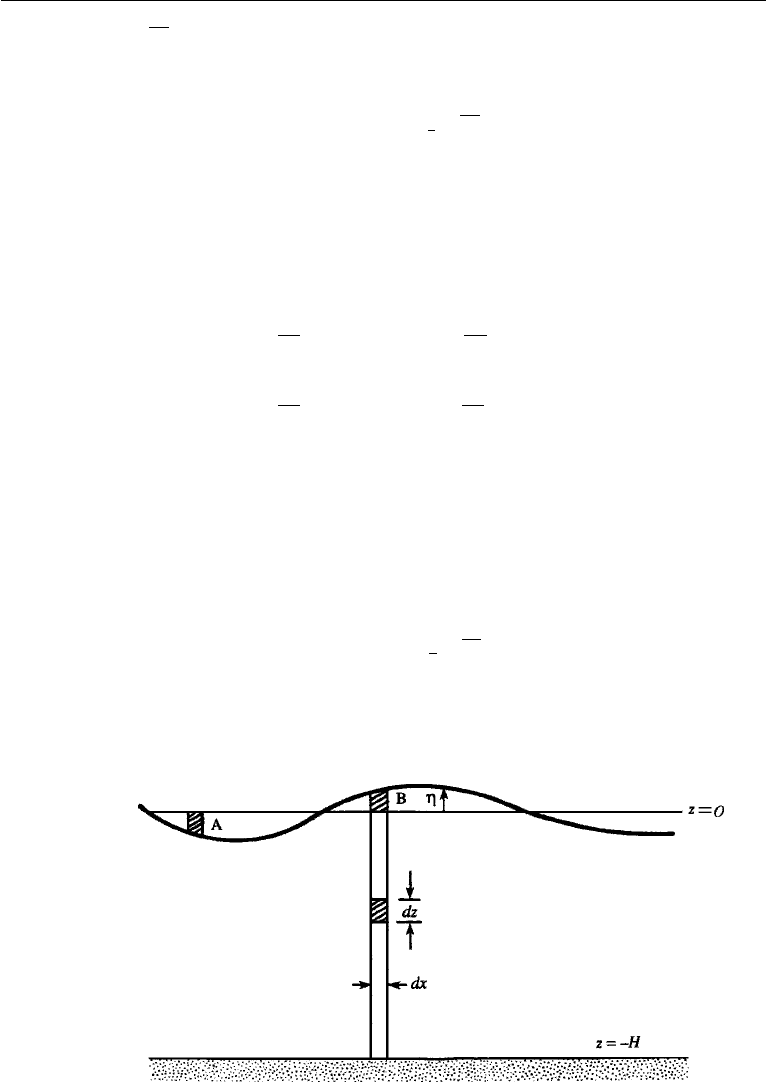
Consider next the potential energy of the wave system, deﬁned as the work done

to deform a horizontal free surface into the disturbed state. It is therefore equal to the

difference of potential energies of the system in the disturbed and undisturbed states.

As the potential energy of an element in the ﬂuid (per unit length in y)isρgz dx dz

(Figure 7.8), the potential energy of the wave system per unit horizontal area is

ρg



−H

zdzdx−

ρg



−H

zdzdx,

ρg



zdzdx =

ρg

2λ



dx. (7.53)

(An easier way to arrive at the expression for E

is to note that the potential energy

increase due to wave motion equals the work done in raising column A in Figure 7.8

to the location of column B, and integrating over half the wavelength. This is because

an interchange of A and B over half a wavelength automatically forms a complete

wavelength of the deformed surface. The mass of column A is ρη dx, and the cen-

ter of gravity is raised by η when A is taken to B. This agrees with the last form

in equation (7.53).) Equation (7.53) can be written in terms of the mean square

displacement as

ρgη

. (7.54)

Comparison of equation (7.52) and equation (7.54) shows that the average kinetic

and potential energies are equal. This is called the principle of equipartition of energy

Figure 7.8 Calculation of potential energy of a ﬂuid column.

6. Approximations for Deep and Shallow Water 229

and is valid in conservative dynamical systems undergoing small oscillations that are

unaffected by planetary rotation. However, it is not valid when Coriolis forces are

included, as will be seen in Chapter 14. The total wave energy in the water column

per unit horizontal area is

E = E

+ E

= ρgη

ρga

, (7.55)

where the last form in terms of the amplitude a is valid if η is assumed sinusoidal,

since the average of cos

x over a wavelength is 1/2.

Next, consider the rate of transmission of energy due to a single sinusoidal com-

ponent of wavenumber k. The energy ﬂux across the vertical plane x = 0 is the

pressure work done by the ﬂuid in the region x<0 on the ﬂuid in the region x>0.

Per unit length of crest, the time average energy ﬂux is (writing p as the sum of a

perturbation p



and a background pressure −ρgz)

F =





−H

pu dz







−H



udz



− ρgu



−H

zdz





−H



udz



, (7.56)

where denotes an average over a wave period; we have used the fact that u=0.

Substituting for p



from equation (7.44a) and u from equation (7.39), equation (7.56)

becomes

F =cos

(kx − ωt)

ρa

k sinh



−H

cosh

k(z + H)dz.

The time average of cos

(kx −ωt) is 1/2. The z-integral can be carried out by writing

it in terms of exponentials. This ﬁnally gives

F =



ρga







1 +

2kH

sinh 2kH



. (7.57)

The ﬁrst factor is the wave energy given in equation (7.55). Therefore, the second

factor must be the speed of propagation of wave energy of component k, called the

group speed. This is discussed in Sections 9 and 10.

6. Approximations for Deep and Shallow Water

The analysis in the preceding section is applicable whatever the magnitude of λ

is in relation to the water depth H . Interesting simpliﬁcations result for H/λ  1

(shallow water) and H/λ  1 (deep water). The expression for phase speed is given

by equation (7.41), namely,

c =



gλ

2π

tanh

2πH

. (7.41)

230 Gravity Waves

Approximations are now derived under two limiting conditions in which

equation (7.41) takes simple forms.

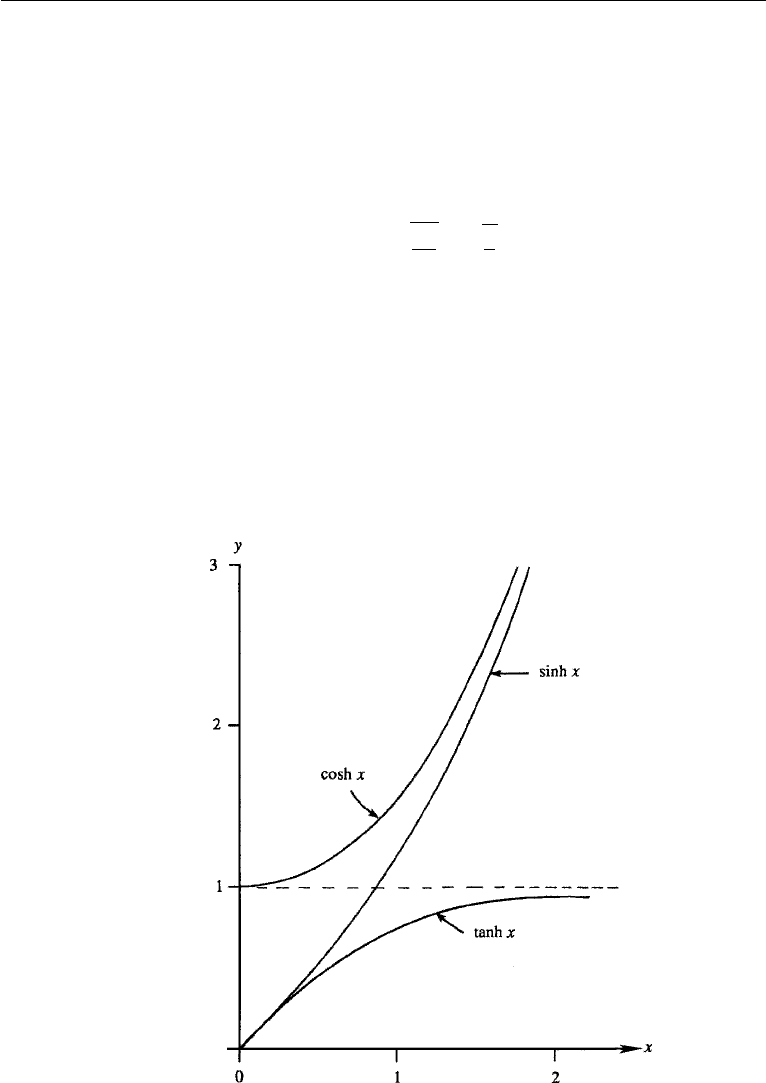
Deep-Water Approximation

We know that tanh x → 1 for x →∞(Figure 7.9). However, x need not be very

large for this approximation to be valid, because tanh x = 0.94138 for x = 1.75. It

follows that, with 3% accuracy, equation (7.41) can be approximated by

c =



gλ

2π



, (7.58)

for H>0.28λ (corresponding to kH > 1.75). Waves are therefore classiﬁed as

deep-water waves if the depth is more than 28% of the wavelength. Equation (7.58)

shows that longer waves in deep water propagate faster. This feature has interesting

consequences and is discussed further in Sections 9 and 10.

A dominant period of wind-generated surface gravity waves in the ocean is ≈10 s,

for which the dispersion relation (7.40) shows that the dominant wavelength is 150 m.

The water depth on a typical continental shelf is ≈100 m, and in the open ocean it

is about ≈4 km. It follows that the dominant wind waves in the ocean, even over the

continental shelf, act as deep-water waves and do not feel the effects of the ocean

Figure 7.9 Behavior of hyperbolic functions.

6. Approximations for Deep and Shallow Water 231

bottom until they arrive near the beach. This is not true of gravity waves generated by

tidal forces and earthquakes; these may have wavelengths of hundreds of kilometers.

In the preceding section we said that particle orbits in small-amplitude gravity

waves describe ellipses given by equation (7.47). For H>0.28λ, the semimajor and

semiminor axes of these ellipses each become nearly equal to ae

. This follows from

the approximation (valid for kH > 1.75)

cosh k(z + H)

sinh kH



sinh k(z + H)

sinh kH

 e

(The various approximations for hyperbolic functions used in this section can easily be

veriﬁed by writing them in terms of exponentials.) Therefore, for deep-water waves,

particle orbits described by equation (7.46) simplify to

ξ =−ae

sin(kx

− ωt)

ζ = ae

cos(kx

− ωt).

The orbits are therefore circles (Figure 7.6a), of which the radius at the surface equals

a, the amplitude of the wave. The velocity components are

u =

∂ξ

∂t

= aωe

cos(kx − ωt)

w =

∂ζ

∂t

= aωe

sin(kx − ωt),

where we have omitted the subscripts on (x

). (For small amplitudes the difference

in velocity at the present and mean positions of a particle is negligible. The distinction

between mean particle positions and Eulerian coordinates is therefore not necessary,

unless ﬁnite amplitude effects are considered, as we will see in Section 14.) The

velocity vector therefore rotates clockwise (for a wave traveling in the positive x

direction) at frequency ω, while its magnitude remains constant at aωe

For deep-water waves, the perturbation pressure given in equation (7.44b) sim-

pliﬁes to



= ρgae

cos(kx − ωt). (7.59)

This shows that pressure change due to the presence of wave motion decays exponen-

tially with depth, reaching 4% of its surface magnitude at a depth of λ/2. A sensor

placed at the bottom cannot therefore detect gravity waves whose wavelengths are

smaller than twice the water depth. Such a sensor acts like a “low-pass ﬁlter,” retaining

longer waves and rejecting shorter ones.

Shallow-Water Approximation

We know that tanh x  x as x → 0 (Figure 7.9). For H/λ  1, we can therefore

write

tanh

2πH



2πH