Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

232 Gravity Waves

in which case the phase speed equation (7.41) simpliﬁes to

c =

√

gH. (7.60)

The approximation gives a better than 3% accuracy if H<0.07λ. Surface waves are

therefore regarded as shallow-water waves if the water depth is <7% of the wave-

length. (The water depth has to be really shallow for waves to behave as shallow-water

waves. This is consistent with the comments made in what follows (equation (7.58)),

that the water depth does not have to be really deep for water to behave as deep-water

waves.) For these waves equation (7.60) shows that the wave speed is independent of

wavelength and increases with water depth.

To determine the approximate form of particle orbits for shallow-water waves,

we substitute the following approximations into equation (7.46):

cosh k(z + H)  1

sinh k(z + H)  k(z + H)

sinh kH  kH.

The particle excursions given in equation (7.46) then become

ξ =−

sin(kx − ωt)

ζ = a



1 +



cos(kx − ωt).

These represent thin ellipses (Figure 7.6c), with a depth-independent semimajor axis

of a/kH and a semiminor axis of a(1 + z/H ), which linearly decreases to zero at

the bottom wall. From equation (7.39), the velocity ﬁeld is found as

u =

aω

cos(kx − ωt)

w = aω



1 +



sin(kx − ωt),

(7.61)

which shows that the vertical component is much smaller than the horizontal

component.

The pressure change from the undisturbed state is found from equation (7.44b)

to be



= ρga cos(kx − ωt) = ρgη, (7.62)

where equation (7.33) has been used to express the pressure change in terms of η. This

shows that the pressure change at any point is independent of depth, and equals the

hydrostatic increase of pressure due to the surface elevation change η. The pressure

6. Approximations for Deep and Shallow Water 233

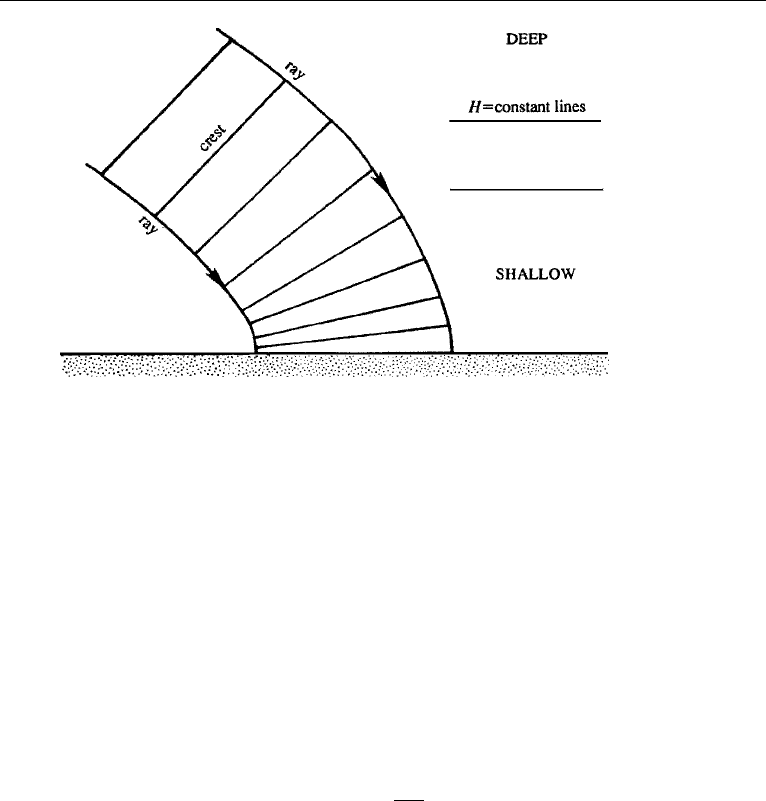
Figure 7.10 Refraction of a surface gravity wave approaching a sloping beach. Note that the crest lines

tend to become parallel to the coast.

ﬁeld is therefore completely hydrostatic in shallow-water waves. Vertical accelera-

tions are negligible because of the small w-ﬁeld. For this reason, shallow water waves

are also called hydrostatic waves. It is apparent that a pressure sensor mounted at the

bottom can sense these waves.

Wave Refraction in Shallow Water

We shall now qualitatively describe the commonly observed phenomenon of refrac-

tion of shallow-water waves. Consider a sloping beach, with depth contours parallel

to the coastline (Figure 7.10). Assume that waves are propagating toward the coast

from the deep ocean, with their crests at an angle to the coastline. Sufﬁciently near the

coastline they begin to feel the effect of the bottom and ﬁnally become shallow-water

waves. Their frequency does not change along the path (a fact that will be proved in

Section 10), but the speed of propagation c =

√

gH and the wavelength λ become

smaller. Consequently, the crest lines, which are perpendicular to the local direction

of c, tend to become parallel to the coast. This is why we see that the waves coming

toward the beach always seem to have their crests parallel to the coastline.

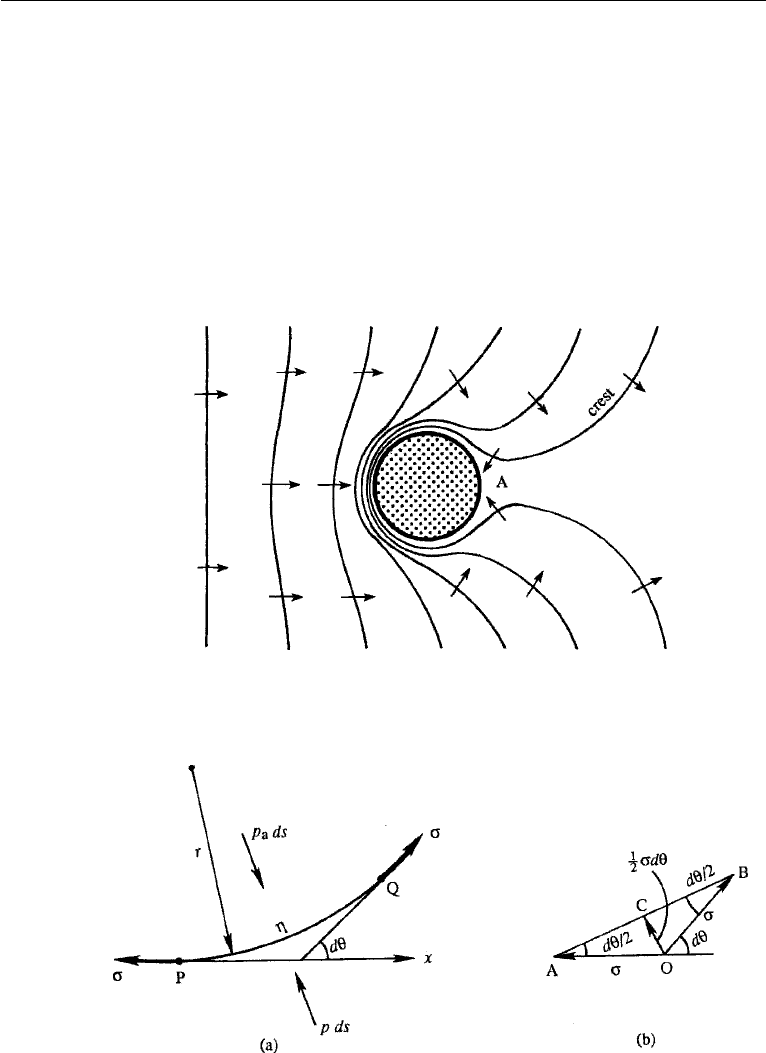
An interesting example of wave refraction occurs when a deep-water wave with

straight crests approaches an island (Figure 7.11). Assume that the water depth

becomes shallower as the island is approached, and the constant depth contours are

circles concentric with the island. Figure 7.11 shows that the waves always come in

toward the island, even on the “shadow” side marked A!

The bending of wave paths in an inhomogeneous medium is called wave refrac-

tion. In this case the source of inhomogeneity is the spatial dependence of H . The

analogous phenomenon in optics is the bending of light due to density changes in

its path.

234 Gravity Waves

7. Inﬂuence of Surface Tension

It was explained in Section 1.5 that the interface between two immiscible ﬂuids is in a

state of tension. The tension acts as a restoring force, enabling the interface to support

waves in a manner analogous to waves on a stretched membrane or string. Waves due

to the presence of surface tension are called capillary waves. Although gravity is not

needed to support these waves, the existence of surface tension alone without gravity

is uncommon. We shall therefore examine the modiﬁcation of the preceding results

for pure gravity waves due to the inclusion of surface tension.

Let PQ = ds be an element of arc on the free surface, whose local radius of

curvature is r (Figure 7.12a). Suppose p

is the pressure on the “atmospheric” side,

and p is the pressure just inside the interface. The surface tension forces at P and Q,

Figure 7.11 Refraction of a surface gravity wave approaching an island with sloping beach. Crest lines,

perpendicular to the rays, are shown. Note that the crest lines come in toward the island, even on the

shadow side A. Reprinted with the permission of Mrs. Dorothy Kinsman Brown: B. Kinsman, Wind Waves,

Prentice-Hall Englewood Cliffs, NJ, 1965.

Figure 7.12 (a) Segment of a free surface under the action of surface tension; (b) net surface tension

force on an element.

7. Inﬂuence of Surface Tension 235

per unit length perpendicular to the plane of the paper, are each equal to σ and directed

along the tangents at P and Q. Equilibrium of forces on the arc PQ is considered in

Figure 7.12b. The force at P is represented by segment OA, and the force at Q is

represented by segment OB. The resultant of OA and OB in a direction perpendicular

to the arc PQ is represented by 2OC  σdθ. Therefore, the balance of forces in a

direction perpendicular to the arc PQ requires

−p

ds + pds+ σdθ = 0.

It follows that the pressure difference is related to the curvature by

− p = σ

dθ

The curvature 1/r of η(x) is given by

∂

η/∂x

[1 + (∂η/∂x)

]

3/2



∂

∂x

where the approximate expression is for small slopes. Therefore,

− p = σ

∂

∂x

Choosing the atmospheric pressure p

to be zero, we obtain the condition

p =−σ

∂

∂x

at z = η. (7.63)

Using the linearized Bernoulli equation

∂φ

∂t

+ gz = 0,

condition (7.63) becomes

∂φ

∂t

∂

∂x

− gη at z = 0. (7.64)

As before, for small-amplitude waves it is allowable to apply the surface boundary

condition (7.64) at z = 0, instead at z = η.

Solution of the wave problem including surface tension is identical to the one for

pure gravity waves presented in Section 4, except that the pressure boundary condition

(7.32) is replaced by (7.64). This only changes the dispersion relation ω(k), which is

found by substitution of (7.33) and (7.38) into (7.64), to give

ω =





g +

σk



tanh kH. (7.65)

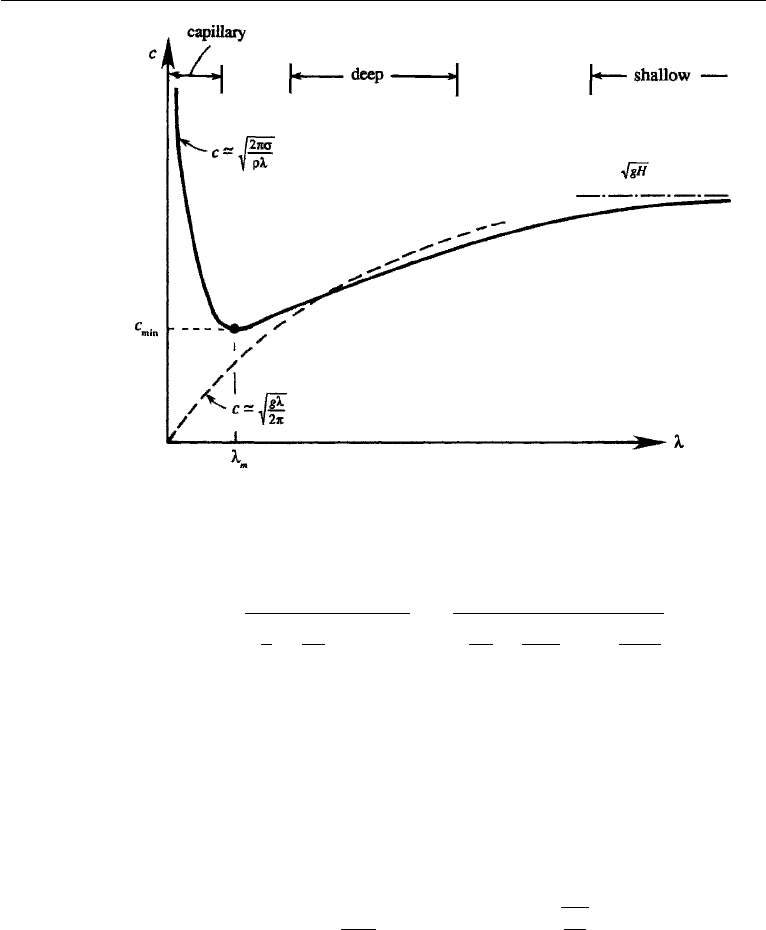
236 Gravity Waves

Figure 7.13 Sketch of phase velocity vs wavelength in a surface gravity wave.

The phase velocity is therefore

c =





σk



tanh kH =





gλ

2π

2πσ

ρλ



tanh

2πH

. (7.66)

A plot of equation (7.66) is shown in Figure 7.13. It is apparent that the effect of surface

tension is to increase c above its value for pure gravity waves at all wavelengths. This

is because the free surface is now “tighter,” and hence capable of generating more

restoring forces. However, the effect of surface tension is only appreciable for very

small wavelengths. A measure of these wavelengths is obtained by noting that there

is a minimum phase speed at λ = λ

, and surface tension dominates for λ<λ

(Figure 7.13). Setting dc/dλ = 0 in equation (7.66), and assuming the deep-water

approximation tanh(2π H /λ)  1 valid for H>0.28λ, we obtain

min



4gσ



1/4

at λ

= 2π



ρg

. (7.67)

For an air–water interface at 20

◦

C, the surface tension is σ = 0.074 N/m, giving

min

= 23.2cm/satλ

= 1.73 cm. (7.68)

Only small waves (say, λ<7 cm for an air–water interface), called ripples, are there-

fore affected by surfacetension. Wavelengths <4 mm are dominated by surface tension

8. Standing Waves 237

and are rather unaffected by gravity. From equation (7.66), the phase speed of these

pure capillary waves is

c =



2πσ

ρλ

, (7.69)

where we have again assumed tanh(2π H/λ)  1. The smallest of these, traveling

at a relatively large speed, can be found leading the waves generated by dropping a

stone into a pond.

8. Standing Waves

So far, we have been studying propagating waves. Nonpropagating waves can be gen-

erated by superposing two waves of the same amplitude and wavelength, but moving

in opposite directions. The resulting surface displacement is

η = a cos(kx − ωt) + a cos(kx + ωt) = 2a cos kx cos ωt.

It follows that η = 0 for kx =±π/2, ±3π/2 .... Points of zero surface displacement

are called nodes. The free surface therefore does not propagate, but simply oscillates

up and down with frequency ω, keeping the nodal points ﬁxed. Such waves are called

standing waves. The corresponding streamfunction, using equation (7.50), is both for

the cos(kx − ωt) and cos(kx + ωt) components, and for the sum. This gives

ψ =

aω

sinh k(z + H)

sinh kH

[cos(kx − ωt) − cos(kx + ωt)]

2aω

sinh k(z + H)

sinh kH

sin kx sin ωt. (7.70)

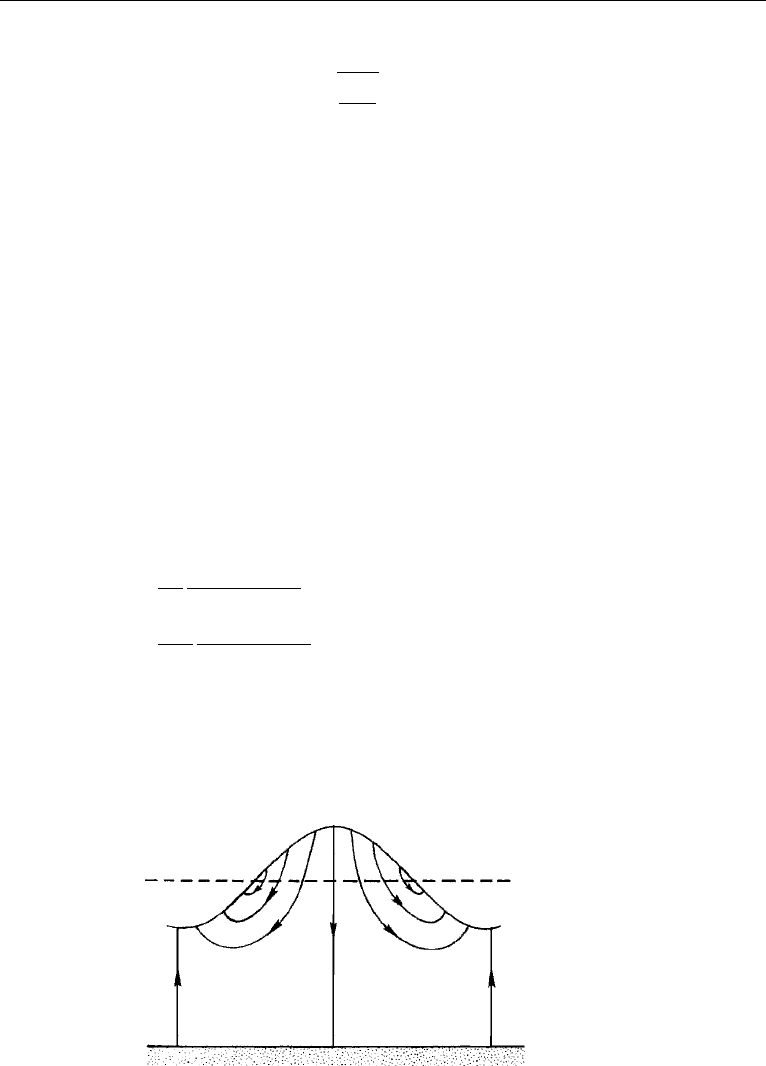
The instantaneous streamline pattern shown in Figure 7.14 should be compared with

the streamline pattern for a propagating wave (Figure 7.7).

A limited body of water such as a lake forms standing waves by reﬂection from

the walls. A standing oscillation in a lake is called a seiche (pronounced “saysh”),

Figure 7.14 Instantaneous streamline pattern in a standing surface gravity wave. If this is mode n = 0,

then two successive vertical streamlines are a distance L apart. If this is mode n = 1, then the ﬁrst and

third vertical streamlines are a distance L apart.

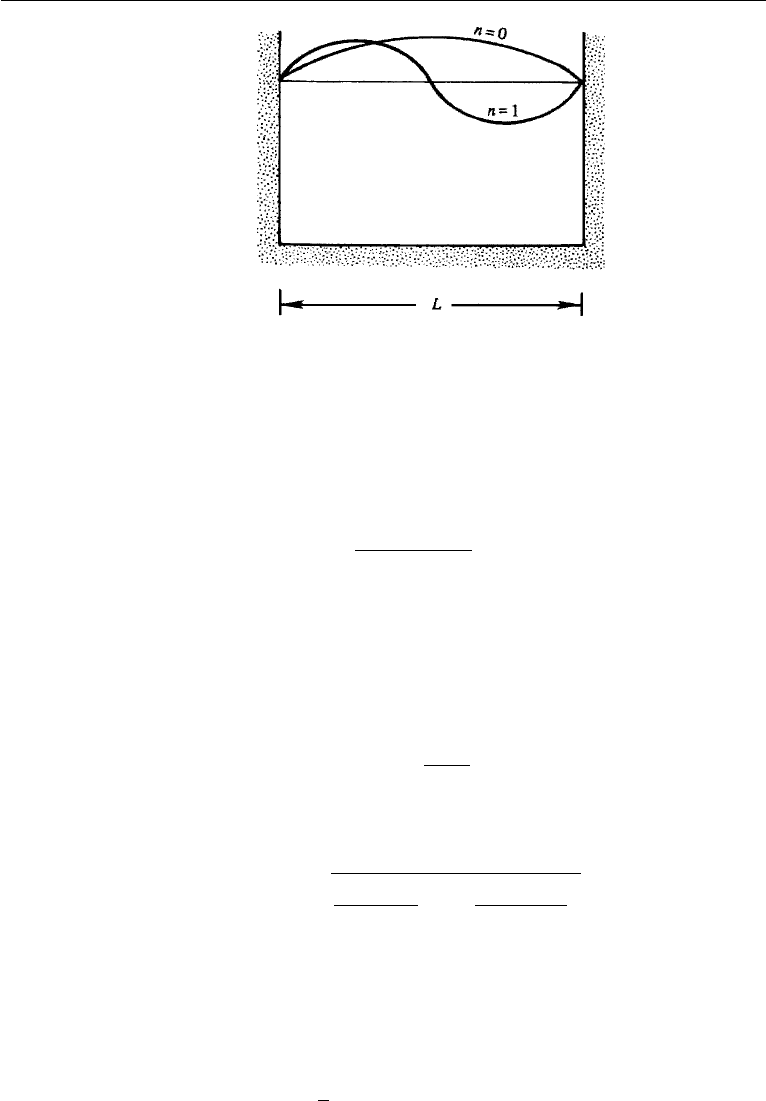
238 Gravity Waves

Figure 7.15 Normal modes in a lake, showing distributions of u for the ﬁrst two modes. This is consistent

with the streamline pattern of Figure 7.14.

in which only certain wavelengths and frequencies ω (eigenvalues) are allowed by

the system. Let L be the length of the lake, and assume that the waves are invariant

along y. The possible wavelengths are found by setting u = 0 at the two walls.

Because u = ∂ψ/∂z, equation (7.70) gives

u = 2aω

cosh k(z + H)

sinh kH

sin kx sin ωt. (7.71)

Taking the walls at x = 0 and L, the condition of no ﬂow through the walls requires

sin(kL) = 0, that is,

kL = (n + 1)π n = 0, 1, 2,...,

which gives the allowable wavelengths as

λ =

n + 1

. (7.72)

The largest wavelength is 2L and the next smaller is L (Figure 7.15). The allowed

frequencies can be found from the dispersion relation (7.40), giving

ω =



πg(n + 1)

tanh



(n + 1)π H



, (7.73)

which are the natural frequencies of the lake.

9. Group Velocity and Energy Flux

An interesting set of phenomena takes place when the phase speed of a wave depends

on its wavelength. The most common example is the deep water gravity wave, for

which c is proportional to

√

λ. A wave phenomenon in which c depends on k is called

9. Group Velocity and Energy Flux 239

dispersive because, as we shall see in the next section, the different wave components

separate or “disperse” from each other.

In a dispersive system, the energy of a wave component does not propagate at

the phase velocity c = ω/k, but at the group velocity deﬁned as c

= dω/dk. To see

this, consider the superposition of two sinusoidal components of equal amplitude but

slightly different wavenumber (and consequently slightly different frequency because

ω = ω(k)). Then the combination has a waveform

η = a cos(k

x − ω

t) + a cos(k

x − ω

t).

Applying the trigonometric identity for cos A + cos B, we obtain

η = 2a cos



− k

)x −

(ω

− ω



cos



+ k

)x −

(ω

+ ω



Writing k = (k

+ k

)/2, ω = (ω

+ ω

)/2, dk = k

− k

, and dω = ω

− ω

we obtain

η = 2a cos



dk x −

dω t



cos(kx − ωt). (7.74)

Here, cos(kx − ωt) is a progressive wave with a phase speed of c = ω/k. However,

its amplitude 2a is modulated by a slowly varying function cos[dk x/2 − dω t/2],

which has a large wavelength 4π/dk, a large period 4π/dω, and propagates at a speed

(=wavelength/period) of

dω

(7.75)

Multiplication of a rapidly varying sinusoid and a slowly varying sinusoid, as in

equation (7.74), generates repeating wave groups (Figure 7.16). The individual wave

components propagate with the speed c = ω/k, but the envelope of the wave groups

travels with the speed c

, which is therefore called the group velocity.Ifc

<c,

then the wave crests seem to appear from nowhere at a nodal point, proceed forward

through the envelope, and disappear at the next nodal point. If, on the other hand,

>c, then the individual wave crests seem to emerge from a forward nodal point

and vanish at a backward nodal point.

node

2 a cos

(dk x

2tdv)

Figure 7.16 Linear combination of two sinusoids, forming repeated wave groups.

240 Gravity Waves

Equation (7.75) shows that the group speed of waves of a certain wavenumber

k is given by the slope of the tangent to the dispersion curve ω(k). In contrast, the

phase velocity is given by the slope of the radius vector (Figure 7.17).

A particularly illuminating example of the idea of group velocity is provided

by the concept of a wave packet, formed by combining all wavenumbers in a cer-

tain narrow band δk around a central value k. In physical space, the wave appears

nearly sinusoidal with wavelength 2π/k, but the amplitude dies away in a length of

order 1/δk (Figure 7.18). If the spectral width δk is narrow, then decay of the wave

amplitude in physical space is slow. The concept of such a wave packet is more real-

istic than the one in Figure 7.16, which is rather unphysical because the wave groups

repeat themselves. Suppose that, at some initial time, the wave group is represented by

η = a(x) cos kx.

It can be shown (see, for example, Phillips (1977), p. 25) that for small times the

subsequent evolution of the wave proﬁle is approximately described by

η = a(x − c

t)cos(kx − ωt), (7.76)

where c

= dω/dk. This shows that the amplitude of a wave packet travels with the

group speed. It follows that c

must equal the speed of propagation of energy of a

certain wavelength. The fact that c

is the speed of energy propagation is also evident

in Figure 7.16 because the nodal points travel at c

and no energy can cross the nodal

points.

For surface gravity waves having the dispersion relation

ω =



gk tanh kH, (7.40)

the group velocity is found to be



1 +

2kH

sinh 2kH



. (7.77)

Figure 7.17 Finding c and c

from dispersion relation ω(k).

9. Group Velocity and Energy Flux 241

Figure 7.18 A wave packet composed of a narrow band of wavenumbers δk.

The two limiting cases are

c (deep water),

= c (shallow water).

(7.78)

The group velocity of deep-water gravity waves is half the phase speed. Shallow-water

waves, on the other hand, are nondispersive, for which c = c

. For a linear nondis-

persive system, any waveform preserves its shape in time because all the wavelengths

that make up the waveform travel at the same speed. For a pure capillary wave, the

group velocity is c

= 3c/2 (Exercise 3).

The rate of transmission of energy for gravity waves is given by equation (7.57),

namely

F = E



1 +

2kH

sinh kH



where E = ρga

/2 is the average energy in the water column per unit horizontal

area. Using equation (7.77), we conclude that

F = Ec

. (7.79)

This signiﬁes that the rate of transmission of energy of a sinusoidal wave component

is wave energy times the group velocity. This reinforces our previous interpretation

of the group velocity as the speed of propagation of energy.

We have discussed the concept of group velocity in one dimension only, taking

ω to be a function of the wavenumber k in the direction of propagation. In three

dimensions ω(k, l, m) is a function of the three components of the wavenumber

vector K = (k,l,m)and, using Cartesian tensor notation, the group velocity vector

is given by

∂ω

∂K

where K

stands for any of the components of K. The group velocity vector is then

the gradient of ω in the wavenumber space.