Cohen I.M., Kundu P.K. Fluid Mechanics
Подождите немного. Документ загружается.


282 Dynamic Similarity
It is clear that the boundary conditions in terms of the nondimensional variables in
equation (8.2) are independent of l and U . For example, consider the viscous flow over
a circular cylinder of radius R. We choose the velocity scale U to be the free-stream
velocity and the length scale to be the radius R. In terms of nondimensional velocity
u
= u/U and the nondimensional coordinate r
= r/R, the boundary condition at
infinity is u
→ 1asr
→∞, and the condition at the surface of the cylinder is
u
= 0atr
= 1. (Here, u is taken to be the r-component of velocity.)
There are instances where the shape function of a body may require two length
scales, such as a length l and a thickness d. An additional dimensionless parameter,
d/l would result to describe the slenderness of the body.
Normalization, that is, dimensionless representation of the pressure, depends on
the dominant effect in the flow unless the flow is pressure-gradient driven. In the
latter case for flow in ducts or tubes, the pressure should be made dimensionless
by a characteristic pressure difference in the duct so that the dimensionless term
is finite. In other cases, when the flow is not pressure-gradient driven, the pressure
is a passive variable and should be normalized to balance the dominant effect in
the flow. Because pressure enters only as a gradient, the pressure itself is not of
consequence; only pressure differences are important. The conventional practice is
to render p − p
∞
dimensionless. Depending on the nature of the flow, this could be
in terms of viscous stress µU/ l, a hydrostatic pressure ρgl, or as in the preceding, a
dynamic pressure ρU
2
.
Substitution of equation (8.2) into equation (8.1) gives
∂w
∂t
+ u
∂w
∂x
+ v
∂w
∂y
+ w
∂w
∂z
=−
∂p
∂z
−
gl
U
2
+
ν
Ul
∂
2
w
∂x
2
+
∂
2
w
∂y
2
+
∂
2
w
∂z
2
.
(8.3)
It is apparent that two flows (having different values of U , l,orν), will obey the same
nondimensional differential equation if the values of nondimensional groups gl/U
2
and ν/Ul are identical. Because the nondimensional boundary conditions are also
identical in the two flows, it follows that they will have the same nondimensional
solutions.
The nondimensional parameters Ul/ν and U/
√
gl have been given special
names:
Re ≡
Ul
ν
= Reynolds number,
Fr ≡
U
√
gl
= Froude number.
(8.4)
Both Re and Fr have to be equal for dynamic similarity of two flows in which both
viscous and gravitational effects are important. Note that the mere presence of gravity
does not make the gravitational effects dynamically important. For flow around an
object in a homogeneous fluid, gravity is important only if surface waves are generated.
Otherwise, the effect of gravity is simply to add a hydrostatic pressure to the entire
system, which can be eliminated by absorbing gravity into the pressure term.

2. Nondimensional Parameters Determined from Differential Equations 283
Under dynamic similarity the nondimensional solutions are identical. Therefore,
the local pressure at point x = (x,y,z)must be of the form
p
(
x
)
− p
∞
ρU
2
= f
Fr, Re;
x
l
, (8.5)
where (p − p
∞
)/ρU
2
is called the pressure coefficient. Similar relations also hold
for any other nondimensional flow variable such as velocity u/U and acceleration
al/U
2
. It follows that in dynamically similar flows the nondimensional local flow
variables are identical at corresponding points (that is, for identical values of x/l).
In the foregoing analysis we have assumed that the imposed boundary conditions
are steady. However, we have retained the time derivative in equation (8.3) because
the resulting flow can still be unsteady; for example, unstable waves can arise spon-
taneously under steady boundary conditions. Such unsteadiness must have a time
scale proportional to l/U, as assumed in equation (8.2). Consider now a situation
in which the imposed boundary conditions are unsteady. To be specific, consider an
object having a characteristic length scale l oscillating with a frequency ω in a fluid
at rest at infinity. This is a problem having an imposed length scale and an imposed
time scale 1/ω. In such a case a velocity scale can be derived from ω and l to be
U = lω. The preceding analysis then goes through, leading to the conclusion that
Re = Ul/ν = ωl
2
/ν and Fr = U/
√
gl = ω
√
l/g have to be duplicated for dynamic
similarity of two flows in which viscous and gravitational effects are important.
All nondimensional quantities are identical for dynamically similar flows. For
flow around an immersed body, we can define a nondimensional drag coefficient
C
D
≡
D
ρU
2
l
2
/2
, (8.6)
where D is the drag experienced by the body; use of the factor of 1/2 in equation (8.6)
is conventional but not necessary. Instead of writing C
D
in terms of a length scale l,
it is customary to define the drag coefficient more generally as
C
D
≡
D
ρU
2
A/2
,
where A is a characteristic area. For blunt bodies such as spheres and cylinders,
A is taken to be a cross section perpendicular to the flow. Therefore, A = πd
2
/4 for
a sphere of diameter d, and A = bd for a cylinder of diameter d and length b, with
the axis of the cylinder perpendicular to the flow. For flow over a flat plate, on the
other hand, A is taken to be the “wetted area”, that is, A = bl; here, l is the length of
the plate in the direction of flow and b is the width perpendicular to the flow.
The values of the drag coefficient C
D
are identical for dynamically similar flows.
In the present example in which the drag is caused both by gravitational and viscous
effects, we must have a functional relation of the form
C
D
= f
(
Fr, Re
)
. (8.7)

284 Dynamic Similarity
For many flows the gravitational effects are unimportant. An example is the flow
around the body, such as an airfoil, that does not generate gravity waves. In that case
Fr is irrelevant, and
C
D
= f
(
Re
)
. (8.8)
We recall from the preceding discussion that speeds are low enough to ignore com-
pressibility effects.
3. Dimensional Matrix
In many complicated flow problems the precise form of the differential equations may
not be known. In this case the conditions for dynamic similarity can be determined
by means of a dimensional analysis of the variables involved. A formal method of
dimensional analysis is presented in the following section. Here we introduce certain
ideas that are needed for performing a formal dimensional analysis.
The underlying principle in dimensional analysis is that of dimensional homo-
geneity, which states that all terms in an equation must have the same dimension. This
is a basic check that we constantly apply when we derive an equation; if the terms do
not have the same dimension, then the equation is not correct.
Fluid flow problems without electromagnetic forces and chemical reactions
involve only mechanical variables (such as velocity and density) and thermal vari-
ables (such as temperature and specific heat). The dimensions of all these vari-
ables can be expressed in terms of four basic dimensions—mass M, length L,
time T, and temperature θ . We shall denote the dimension of a variable q
by [q]. For example, the dimension of velocity is [u]=L/T, that of pres-
sure is [p]=[force]/[area]=MLT
−2
/L
2
= M/LT
2
, and that of specific heat
is [C]=[energy]/[mass][temperature]=MLT
−2
L/Mθ = L
2
/θT
2
. When thermal
effects are not considered, all variables can be expressed in terms of three fundamen-
tal dimensions, namely, M, L, and T. If temperature is considered only in combination
with Boltzmann’s constant (kθ) or a gas constant (Rθ), then the units of the combi-
nation are simply L
2
/T
2
. Then only the three dimensions M, L, and T are required.
The method of dimensional analysis presented here uses the idea of a “dimen-
sional matrix” and its rank. Consider the pressure drop p in a pipeline, which is
expected to depend on the inside diameter d of the pipe, its length l, the average size
e of the wall roughness elements, the average flow velocity U , the fluid density ρ,
and the fluid viscosity µ. We can write the functional dependence as
f
(
p,d,l,e,U,ρ,µ
)
= 0. (8.9)
The dimensions of the variables can be arranged in the form of the following matrix:
p d l e U ρ µ
M
1000011
L
−11111−3 −1
T
−2000−10−1
(8.10)

4. Buckingham’s Pi Theorem 285
Where we have written the variables p,d,...on the top and their dimensions in a
vertical column underneath. For example, [p ]=ML
−1
T
−2
. An array of dimensions
such as equation (8.10) is called a dimensional matrix. The rank r of any matrix is
defined to be the size of the largest square submatrix that has a nonzero determinant.
Testing the determinant of the first three rows and columns, we obtain
100
−111
−200
= 0.
However, there does exist a nonzero third-order determinant, for example, the one
formed by the last three columns:
011
1 −3 −1
−10−1
=−1.
Thus, the rank of the dimensional matrix (8.10) is r = 3. If all possible third-order
determinants were zero, we would have concluded that r<3 and proceeded to test
the second-order determinants.
It is clear that the rank is less than the number of rows only when one of the rows
can be obtained by a linear combination of the other rows. For example, the matrix
(not from equation (8.10)):
0101
−121−2
−1410
has r = 2, as the last row can be obtained by adding the second row to twice the first
row. A rank of less than 3 commonly occurs in problems of statics, in which the mass
is really not relevant in the problem, although the dimensions of the variables (such
as force) involve M. In most problems in fluid mechanics without thermal effects,
r = 3.
4. Buckingham’s Pi Theorem
Of the various formal methods of dimensional analysis, the one that we shall describe
was proposed by Buckingham in 1914. Let q
1
,q
2
,...,q
n
be n variables involved in
a particular problem, so that there must exist a functional relationship of the form
f
(
q
1
,q
2
,...,q
n
)
= 0. (8.11)
Buckingham’s theorem states that the n variables can always be combined to form
exactly (n − r) independent nondimensional variables, where r is the rank of the
dimensional matrix. Each nondimensional parameter is called a “ number,” or more
commonly a nondimensional product. (The symbol is used because the nondimen-
sional parameter can be written as a product of the variables q
1
,...,q
n
, raised to

286 Dynamic Similarity
some power, as we shall see.) Thus, equation (8.11) can be written as a functional
relationship
φ
(
1
,
2
,...,
n−r
)
= 0. (8.12)
It will be seen shortly that the nondimensional parameters are not unique. However,
(n − r) of them are independent and form a complete set.
The method of forming nondimensional parameters proposed by Buckingham is
best illustrated by an example. Consider again the pipe flow problem expressed by
f
(
p,d,l,e,U,ρ,µ
)
= 0, (8.13)
whose dimensional matrix (8.10) has a rank of r = 3. Since there are n = 7 variables
in the problem, the number of nondimensional parameters must be n − r = 4. We
first select any 3 (= r) of the variables as “repeating variables”, which we want to be
repeated in all of our nondimensional parameters. These repeating variables must have
different dimensions, and among them must contain all the fundamental dimensions
M, L, and T. In many fluid flow problems we choose a characteristic velocity, a
characteristic length, and a fluid property as the repeating variables. For the pipe flow
problem, let us choose U , d, and ρ as the repeating variables. Although other choices
would result in a different set of nondimensional products, we can always obtain other
complete sets by combining the ones we have. Therefore, any choice of the repeating
variables is satisfactory.
Each nondimensional product is formed by combining the three repeating vari-
ables with one of the remaining variables. For example, let the first dimensional
product be taken as
1
= U
a
d
b
ρ
c
p .
The exponents a, b, and c are obtained from the requirement that
1
is dimensionless.
This requires
M
0
L
0
T
0
=
LT
−1
a
(
L
)
b
ML
−3
c
ML
−1
T
−2
= M
c+1
L
a+b−3c−1
T
−a−2
.
Equating indices, we obtain a =−2, b = 0, c =−1, so that
1
= U
−2
d
0
ρ
−1
p =
p
ρU
2
.
A similar procedure gives
2
= U
a
d
b
ρ
c
l =
l
d
,
3
= U
a
d
b
ρ
c
e =
e
d
,
4
= U
a
d
b
ρ
c
µ =
µ
ρUd
.

5. Nondimensional Parameters and Dynamic Similarity 287
Therefore, the nondimensional representation of the problem has the form
p
ρU
2
= φ
l
d
,
e
d
,
µ
ρUd
. (8.14)
Other dimensionless products can be obtained by combining the four in the preceding.
For example, a group p d
2
ρ/µ
2
can be formed from
1
/
2
4
. Also, different nondi-
mensional groups would have been obtained had we taken variables other than U , d,
and ρ as the repeating variables. Whatever nondimensional groups we obtain, only
four of these are independent for the pipe flow problem described by equation (8.13).
However, the set in equation (8.14) contains the most commonly used nondimen-
sional parameters, which have familiar physical interpretation and have been given
special names. Several of the common dimensionless parameters will be discussed in
Section 7.
The pi theorem is a formal method of forming dimensionless groups. With some
experience, it becomes quite easy to form the dimensionless numbers by simple
inspection. For example, since there are three length scales d, e, and l in equa-
tion (8.13), we can form two groups such as e/d and l/d. We can also form p/ρU
2
as our dependent nondimensional variable; the Bernoulli equation tells us that ρU
2
has the same units as p. The nondimensional number that describes viscous effects
is well known to be ρUd/µ. Therefore, with some experience, we can find all the
nondimensional variables by inspection alone, thus no formal analysis is needed.
5. Nondimensional Parameters and Dynamic Similarity
Arranging the variables in terms of dimensionless products is especially useful in
presenting experimental data. Consider the case of drag on a sphere of diameter d
moving at a speed U through a fluid of density ρ and viscosity µ. The drag force can
be written as
D = f
(
d,U,ρ,µ
)
. (8.15)
If we do not form dimensionless groups, we would have to conduct an experiment
to determine D vs d, keeping U, ρ, and µ fixed. We would then have to conduct an
experiment to determine D as a function of U , keeping d, ρ, and µ fixed, and so on.
However, such a duplication of effort is unnecessary if we write equation (8.15) in
terms of dimensionless groups. A dimensional analysis of equation (8.15) gives
D
ρU
2
d
2
= f
ρUd
µ
, (8.16)
reducing the number of variables from five to two, and consequently a single experi-
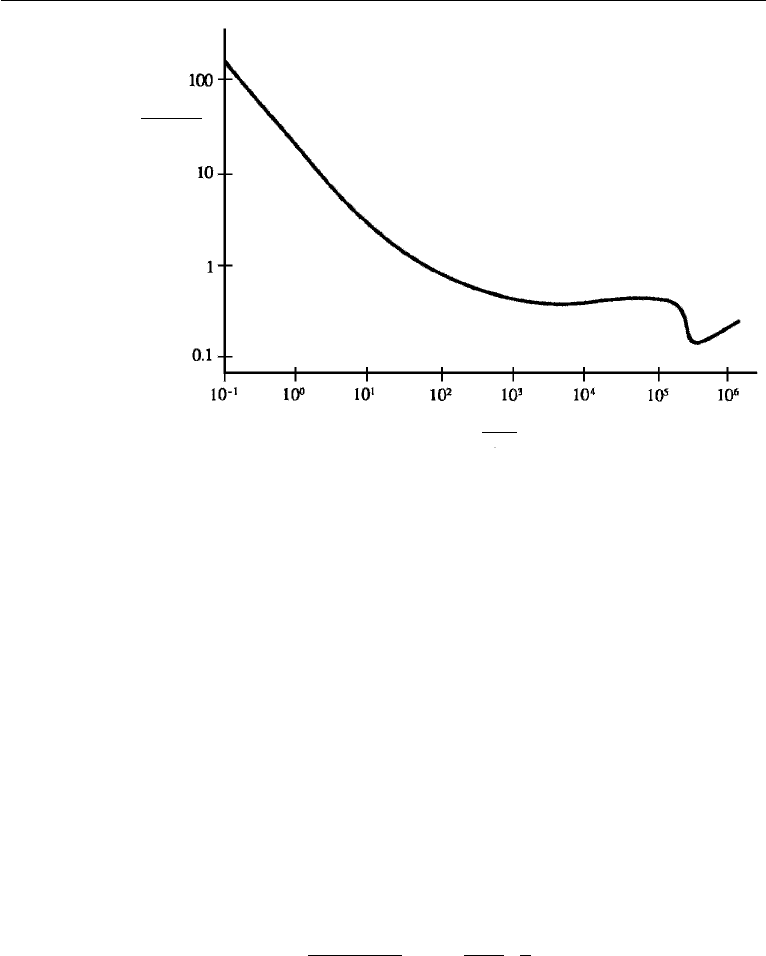
mental curve (Figure 8.2). Not only is the presentation of data united and simplified,
the cost of experimentation is drastically reduced. It is clear that we need not vary
the fluid viscosity or density at all; we could obtain all the data of Figure 8.2 in one
wind tunnel experiment in which we determine D for various values of U . However,
if we want to find the drag force for a fluid of different density or viscosity, we can
288 Dynamic Similarity
C
D
=
½
ρU
2
A
D
Re =
µ
ρUd
()
Figure 8.2 Drag coefficient for a sphere. The characteristic area is taken as A = πd
2
/4. The reason for
the sudden drop of C
D
at Re ∼ 5 ×10
5
is the transition of the laminar boundary layer to a turbulent one,
as explained in Chapter 10.
still use Figure 8.2. Note that the Reynolds number in equation (8.16) is written as
the independent variable because it can be externally controlled in an experiment. In
contrast, the drag coefficient is written as a dependent variable.
The idea of dimensionless products is intimately associated with the concept
of similarity. In fact, a collapse of all the data on a single graph such as the one in
Figure 8.2 is possible only because in this problem all flows having the same value
of Re = ρUd/µ are dynamically similar.
For flow around a sphere, the pressure at any point x =
(
x,y,z
)
can be written as
p
(
x
)
− p
∞
= f
(
d,U,ρ,µ;x
)
.
A dimensional analysis gives the local pressure coefficient:
p
(
x
)
− p
∞
ρU
2
= f
ρUd
µ
;
x
d
, (8.17)
requiring that nondimensional local flow variables be identical at corresponding points
in dynamically similar flows. The difference between relations (8.16) and (8.17)
should be noted. equation (8.16) is a relation between overall quantities (scales of
motion), whereas (8.17) holds locally at a point.

5. Nondimensional Parameters and Dynamic Similarity 289
Prediction of Flow Behavior from Dimensional Considerations
An interesting observation in Figure 8.2 is that C
D
∝ 1/Re at small Reynolds
numbers. This can be justified solely on dimensional grounds as follows. At small
values of Reynolds numbers we expect that the inertia forces in the equations of
motion must become negligible. Then ρ drops out of equation (8.15), requiring
D = f
(
d,U,µ
)
.
The only dimensionless product that can be formed from the preceding is D/µU d.
Because there is no other nondimensional parameter on which D/µU d can depend,
it can only be a constant:
D ∝ µUd
(
Re 1
)
, (8.18)
which is equivalent to C
D
∝ 1/Re. It is seen that the drag force in a low Reynolds
number flow is linearly proportional to the speed U; this is frequently called the Stokes
law of resistance.
At the opposite extreme, Figure 8.2 shows that C
D
becomes independent of Re
for values of Re > 10
3
. This is because the drag is now due mostly to the formation
of a turbulent wake, in which the viscosity only has an indirect influence on the flow.
(This will be clear in Chapter 13, where we shall see that the only effect of viscosity
as Re →∞is to dissipate the turbulent kinetic energy at increasingly smaller scales.
The overall flow is controlled by inertia forces alone.) In this limit µ drops out of
equation (8.15), giving
D = f
(
d,U,ρ
)
.
The only nondimensional product is then D/ρU
2
d
2
, requiring
D ∝ ρU
2
d
2
(
Re 1
)
, (8.19)
which is equivalent to C
D
= const. It is seen that the drag force is proportional to U
2
for high Reynolds number flows. This rule is frequently applied to estimate various
kinds of wind forces such as those on industrial structures, houses, automobiles, and
the ocean surface. Consideration of surface tension effects may introduce additional
dimensionless parameters depending on the nature of the problem. For example, if
surface tension is to balance against a gravity body force, the Bond number Bo =
ρgl
2
/σ would be the appropriate dimensionless parameter to consider. If surface
tension is in competition with a viscous stress, then it would be the capillary number,
Ca = µU/σ . Similarly, the Weber number expresses the ratio of inertial forces to
surface tension forces.
It is clear that very useful relationships can be established based on sound physical
considerations coupled with a dimensional analysis. In the present case this procedure
leads to D ∝ µUd for low Reynolds numbers, and D ∝ ρU
2
d
2
for high Reynolds
numbers. Experiments can then be conducted to see if these relations do hold and to
determine the unknown constants in these relations. Such arguments are constantly
used in complicated fluid flow problems such as turbulence, where physical intuition

290 Dynamic Similarity
plays a key role in research. A well-known example of this is the Kolmogorov K
−5/3
spectral law of isotropic turbulence presented in Chapter 13.
6. Comments on Model Testing
The concept of similarity is the basis of model testing, in which test data on one flow
can be applied to other flows. The cost of experimentation with full-scale objects
(which are frequently called prototypes) can be greatly reduced by experiments on
a smaller geometrically similar model. Alternatively, experiments with a relatively
inconvenient fluid such as air or helium can be substituted by an experiment with an
easily workable fluid such as water. A model study is invariably undertaken when a
new aircraft, ship, submarine, or harbor is designed.
In many flow situations both friction and gravity forces are important, which
requires that both the Reynolds number and the Froude number be duplicated in a
model testing. Since Re = Ul/ν and Fr = U/
√
gl, simultaneous satisfaction of both
criteria would require U ∝ 1/l and U ∝
√
l as the model length is varied. It follows
that both the Reynolds and the Froude numbers cannot be duplicated simultaneously
unless fluids of different viscosities are used in the model and the prototype flows.
This becomes impractical, or even impossible, as the requirement sometimes needs
viscosities that cannot be met by common fluids. It is then necessary to decide which
of the two forces is more important in the flow, and a model is designed on the
basis of the corresponding dimensionless number. Corrections can then be applied to
account for the inequality of the remaining dimensionless group. This is illustrated
in Example 8.1, which follows this section.
Although geometric similarity is a precondition to dynamic similarity, this is
not always possible to attain. In a model study of a river basin, a geometrically
similar model results in a stream so shallow that capillary and viscous effects become
dominant. In such a case it is necessary to use a vertical scale larger than the horizontal
scale. Such distorted models lack complete similitude, and their results are corrected
before making predictions on the prototype.
Models of completely submerged objects are usually tested in a wind tunnel or
in a towing tank where they are dragged through a pool of water. The towing tank
is also used for testing models that are not completely submerged, for example, ship
hulls; these are towed along the free surface of the liquid.
Example 8.1. A ship 100 m long is expected to sail at 10 m/s. It has a submerged
surface of 300 m
2
. Find the model speed for a 1/25 scale model, neglecting frictional
effects. The drag is measured to be 60 N when the model is tested in a towing tank at
the model speed. Based on this information estimate the prototype drag after making
corrections for frictional effects.
Solution: We first estimate the model speed neglecting frictional effects. Then
the nondimensional drag force depends only on the Froude number:
D/ρU
2
l
2
= f
U/
gl
. (8.20)

6. Comments on Model Testing 291
Equating Froude numbers for the model (denoted by subscript “m”) and prototype
(denoted by subscript “p”), we get
U
m
= U
p
g
m
l
m
/g
p
l
p
= 10
1/25 = 2m/s.
The total drag on the model was measured to be 60 N at this model speed. Of
the total measured drag, a part was due to frictional effects. The frictional drag can
be estimated by treating the surface of the hull as a flat plate, for which the drag
coefficient C
D
is given in Figure 10.12 as a function of the Reynolds number. Using
a value of ν = 10
−6
m
2
/s for water, we get
Ul/ν
(
model
)
=[2
(
100/25
)
]/10
−6
= 8 × 10
6
,
Ul/ν
(
prototype
)
= 10
(
100
)
/10
−6
= 10
9
.
For these values of Reynolds numbers, Figure 10.12 gives the frictional drag coeffi-
cients of
C
D
(
model
)
= 0.003,
C
D
(
prototype
)
= 0.0015.
Using a value of ρ = 1000 kg/m
3
for water, we estimate
Frictional drag on model =
1
2
C
D
ρU
2
A
= 0.5
(
0.003
)(
1000
)(
2
)
2
300/25
2
= 2.88 N
Out of the total model drag of 60 N, the wave drag is therefore 60 −2.88 = 57.12 N.
Now the wave drag still obeys equation (8.20), which means that D/ρU
2
l
2
for
the two flows are identical, where D represents wave drag alone. Therefore
Wave drag on prototype
=
(
Wave drag on model
)
ρ
p
/ρ
m
l
p
/l
m
2
U
p
/U
m
2
= 57.12
(
1
)(
25
)
2
(
10/2
)
2
= 8.92 × 10
5
N
Having estimated the wave drag on the prototype, we proceed to determine its
frictional drag. We obtain
Frictional drag on prototype =
1
2
C
D
ρU
2
A
=
(
0.5
)(
0.0015
)(
1000
)(
10
)
2
(
300
)
= 0.225 × 10
5
N
Therefore, total drag on prototype = (8.92 + 0.225) × 10
5
= 9.14 × 10
5
N.
If we did not correct for the frictional effects, and assumed that the measured
model drag was all due to wave effects, then we would have found from equation (8.20)
a prototype drag of
D
p
= D
m
ρ
p
/ρ
m
l
p
/l
m
2
U
p
/U
m
2
= 60
(
1
)(
25
)
2
(
10/2
)
2
= 9.37 × 10
5
N.
