Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

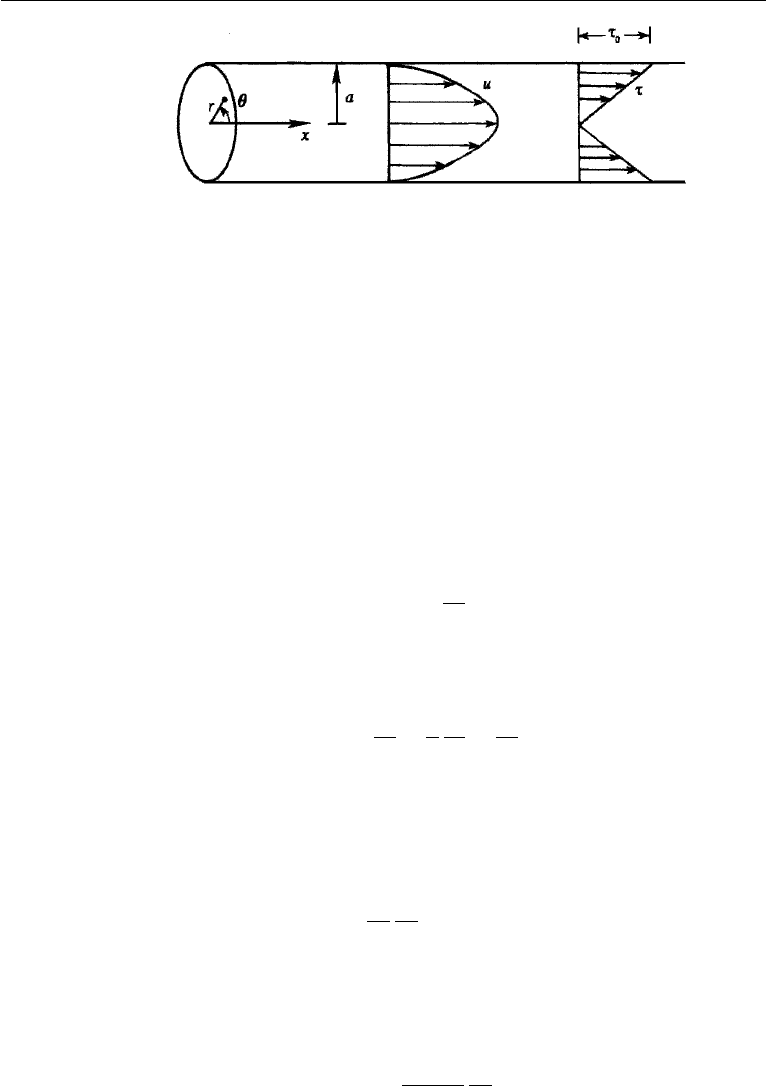
302 Laminar Flow

Figure 9.5 Laminar ﬂow through a tube.

where we have introduced subscripts on τ and noted that the other stress components

are zero. As the left-hand side of the equation is zero, it follows that dp/dx must be

a constant and τ

must be linear in y.

5. Steady Flow in a Pipe

Consider the fully developed laminar motion through a tube of radius a. Flow through

a tube is frequently called a circular Poiseuille ﬂow. We employ cylindrical coordi-

nates (r,θ,x), with the x-axis coinciding with the axis of the pipe (Figure 9.5).

The only nonzero component of velocity is the axial velocity u(r) (omitting the

subscript “x”onu), and none of the ﬂow variables depend on θ. The equations of

motion in cylindrical coordinates are given in Appendix B. The radial equation of

motion gives

0 =−

∂p

∂r

showing that p is a function of x alone. The x-momentum equation gives

0 =−





As the ﬁrst term can only be a function of x, and the second term can only be a

function of r, it follows that both terms must be constant. The pressure therefore falls

linearly along the length of pipe. Integrating twice, we obtain

u =

4µ

+ A ln r + B.

Because u must be bounded at r = 0, we must have A = 0. The wall condition u = 0

at r = a gives B =−(a

/4µ)(dp/dx). The velocity distribution therefore takes the

parabolic shape

u =

− a

4µ

. (9.10)

6. Steady Flow between Concentric Cylinders 303

From Appendix B, the shear stress at any point is

= µ



∂u

∂x

∂u

∂r



In the present case the radial velocity u

is zero. Dropping the subscript on τ ,we

obtain

τ = µ

, (9.11)

which shows that the stress distribution is linear, having a maximum value at the

wall of

. (9.12)

As in the previous section, equation (9.12) is also valid for turbulent ﬂows.

The volume rate of ﬂow is

Q =



u2 πr dr =−

πa

8µ

where the negative sign offsets the negative value of dp/dx. The average velocity

over the cross section is

V ≡

πa

=−

8µ

6. Steady Flow between Concentric Cylinders

Another example in which the nonlinear advection terms drop out of the equations of

motion is the steady ﬂow between two concentric, rotating cylinders. This is usually

called the circular Couette ﬂow to distinguish it from the plane Couette ﬂow in which

the walls are ﬂat surfaces. Let the radius and angular velocity of the inner cylinder be

and 

and those for the outer cylinder be R

and 

(Figure 9.6). Using cylindrical

coordinates, the equations of motion in the radial and tangential directions are

−

=−

0 = µ



(ru

)



The r-momentum equation shows that the pressure increases radially outward due

to the centrifugal force. The pressure distribution can therefore be determined once

(r)has been found. Integrating the θ-momentum equation twice, we obtain

= Ar +

. (9.13)

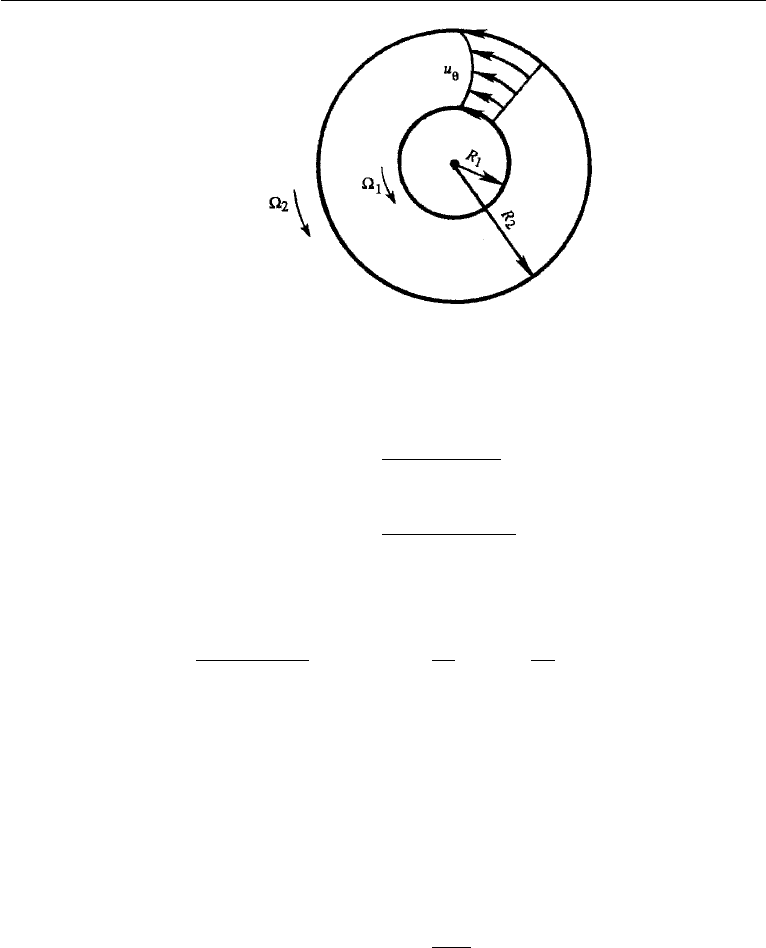
304 Laminar Flow

Figure 9.6 Circular Couette ﬂow.

Using the boundary conditions u

= 

at r = R

, and u

= 

at r = R

we obtain

A =



− 

− R

B =

(

− 

− R

Substitution into equation (9.13) gives the velocity distribution

1 −

(

)





− 







r +

(

− 

)



. (9.14)

Two limiting cases of the velocity distribution are considered in the following.

Flow Outside a Cylinder Rotating in an Inﬁnite Fluid

Consider a long circular cylinder of radius R rotating with angular velocity  in an

inﬁnite body of viscous ﬂuid (Figure 9.7). The velocity distribution for the present

problem can be derived from equation (9.14) if we substitute 

= 0, R

=∞,



= , and R

= R. This gives

R

, (9.15)

which shows that the velocity distribution is that of an irrotational vortex for which the

tangential velocity is inversely proportional to r. As discussed in Chapter 5, Section 3,

this is the only example in which the viscous solution is completely irrotational. Shear

stresses do exist in this ﬂow, but there is no net viscous force at a point. The shear

stress at any point is given by

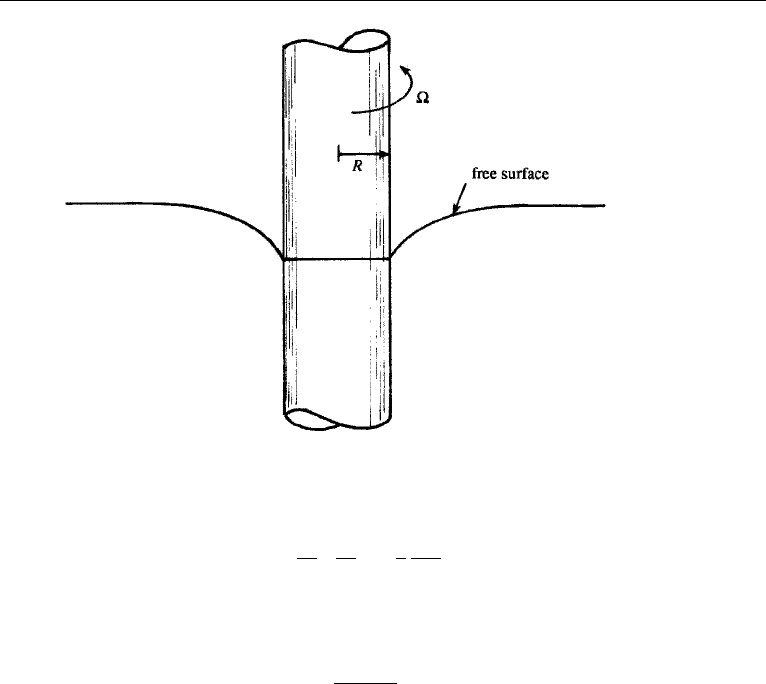
6. Steady Flow between Concentric Cylinders 305

Figure 9.7 Rotation of a solid cylinder of radius R in an inﬁnite body of viscous ﬂuid. The shape of the

free surface is also indicated. The ﬂow ﬁeld is viscous but irrotational.

rθ

= µ



∂

∂r





∂u

∂θ



which, for the present case, reduces to

rθ

=−

2µR

The forcing agent performs work on the ﬂuid at the rate

2πRu

rθ

It is easy to show that this rate of work equals the integral of the viscous dissipation

over the ﬂow ﬁeld (Exercise 4).

Flow Inside a Rotating Cylinder

Consider the steady rotation of a cylindrical tank containing a viscous ﬂuid. The

radius of the cylinder is R, and the angular velocity of rotation is  (Figure 9.8). The

ﬂow would reach a steady state after the initial transients have decayed. The steady

velocity distribution for this case can be found from equation (9.14) by substituting



= 0, R

= 0, 

= , and R

= R.Weget

= r, (9.16)

306 Laminar Flow

Figure 9.8 Steady rotation of a tank containing viscous ﬂuid. The shape of the free surface is also

indicated.

which shows that the tangential velocity is directly proportional to the radius, so that

the ﬂuid elements move as in a rigid solid. This ﬂow was discussed in greater detail

in Chapter 5, Section 3.

7. Impulsively Started Plate: Similarity Solutions

So far, we have considered steady ﬂows with parallel streamlines, both straight and

circular. The nonlinear terms dropped out and the velocity became a function of one

spatial coordinate only. In the transient counterparts of these problems in which the

ﬂow is impulsively started from rest, the ﬂow depends on a spatial coordinate and

time. For these problems, exact solutions still exist because the nonlinear advection

terms drop out again. One of these transient problems is given as Exercise 6. However,

instead of considering the transient phase of all the problems already treated in the

preceding sections, we shall consider several simpler and physically more revealing

unsteady ﬂow problems in this and the next three sections. First, consider the ﬂow

due to the impulsive motion of a ﬂat plate parallel to itself, which is frequently called

Stokes’ ﬁrst problem. (The problem is sometimes unfairly associated with the name of

Rayleigh, who used Stokes’ solution to predict the thickness of a developing boundary

layer on a semi-inﬁnite plate.)

Formulation of a Problem in Similarity Variables

Consider an inﬁnite ﬂat plate along y = 0, surrounded by ﬂuid (with constant ρ

and µ) for y>0. The plate is impulsively given a velocity U at t = 0 (Figure 9.9).

Since the resulting ﬂow is invariant in the x direction, the continuity equation

∂u/∂x + ∂v/∂y = 0 requires ∂v/∂y = 0. It follows that v = 0 everywhere because

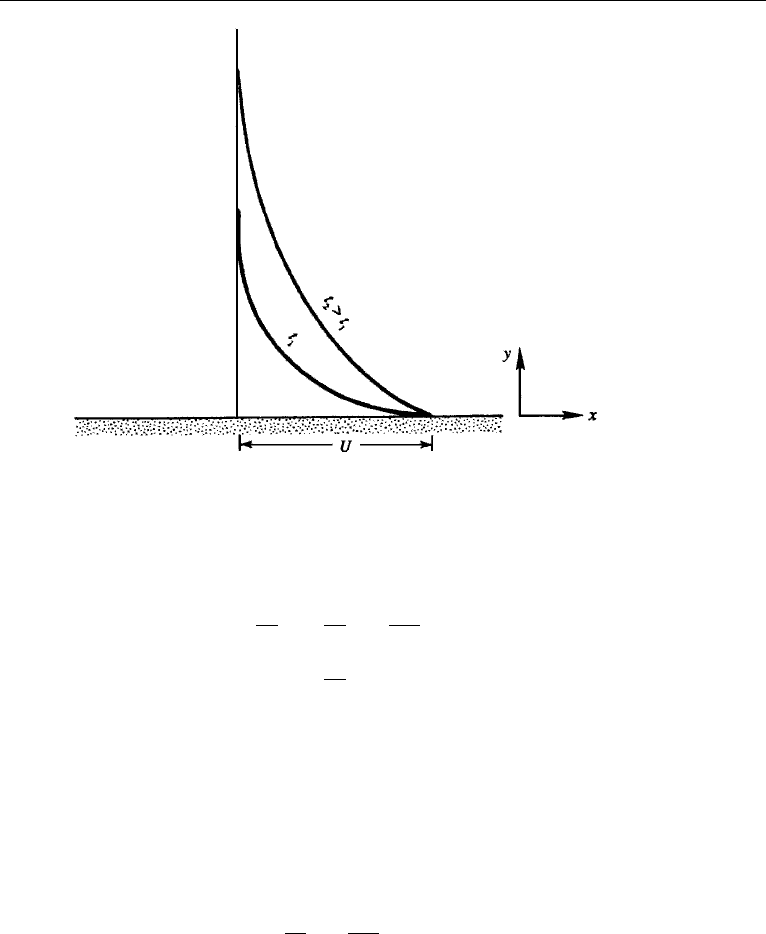
7. Impulsively Started Plate: Similarity Solutions 307

Figure 9.9 Laminar ﬂow due to an impulsively started ﬂat plate.

it is zero at y = 0. If the pressures at x =±∞are maintained at the same level,

we can show that the pressure gradients are zero everywhere as follows. The x- and

y-momentum equations are

∂u

∂t

=−

∂p

∂x

+ µ

∂

∂y

0 =−

∂p

∂y

The y-momentum equation shows that p can only be a function of x and t. This can

be consistent with the x-momentum equation, in which the ﬁrst and the last terms

can only be functions of y and t only if ∂p/∂x is independent of x. Maintenance

of identical pressures at x =±∞therefore requires that ∂p/∂x = 0. Alternatively,

this can be established by observing that for an inﬁnite plate the problem must be

invariant under translation of coordinates by any ﬁnite constant in x.

The governing equation is therefore

∂u

∂t

= ν

∂

∂y

, (9.17)

subject to

u(y, 0) = 0 [initial condition], (9.18)

u(0,t) = U [surface condition], (9.19)

u(∞,t) = 0 [far ﬁeld condition]. (9.20)

308 Laminar Flow

The problem is well posed, because equations (9.19) and (9.20) are conditions at two

values of y, and equation (9.18) is a condition at one value of t; this is consistent with

equation (9.17), which involves a ﬁrst derivative in t and a second derivative in y.

The partial differential equation (9.17) can be transformed into an ordinary

differential equation from dimensional considerations alone. Its real reason is the

absence of scales for y and t as discussed on page 287. Let us write the solution as a

functional relation

u = φ(U, y, t,ν). (9.21)

An examination of the equation set (9.17)–(9.20) shows that the parameter U appears

only in the surface condition (9.19). This dependence on U can be eliminated from

the problem by regarding u/U as the dependent variable, for then the equation set

(9.17)–(9.20) can be written as

∂u



∂t

= ν

∂



∂y



(y, 0) = 0 ,



(0,t) = 1,



(∞,t) = 0,

where u



≡ u/U . The preceding set is independent of U and must have a solution of

the form

= f (y, t, ν). (9.22)

Because the left-hand side of equation (9.22) is dimensionless, the right-hand side

can only be a dimensionless function of y,t, and ν. The only nondimensional variable

formed from y,t, and ν is y/

√

νt, so that equation (9.22) must be of the form

= F



√

νt



. (9.23)

Any function of y/

√

vt would be dimensionless and could be used as the new inde-

pendent variable. Why have we chosen to write it this way rather than νt/y

or some

other equivalent form? We have done so because we want to solve for a velocity proﬁle

as a function of distance from the plate. By thinking of the solution to this problem in

this way, our new dimensionless similarity variable will feature y in the numerator to

the ﬁrst power. We could have obtained equation (9.23) by applying Buckingham’s pi

theorem discussed in Chapter 8, Section 4. There are four variables in equation (9.22),

and two basic dimensions are involved, namely, length and time. Two dimensionless

variables can therefore be formed, and they are shown in equation (9.23).

We write equation (9.23) in the form

= F(η), (9.24)

7. Impulsively Started Plate: Similarity Solutions 309

where η is the nondimensional distance given by

η ≡

√

νt

. (9.25)

We see that the absence of scales for length and time resulted in a reduction of the

dimensionality of the space required for the solution (from 2 to 1). The factor of

2 has been introduced in the deﬁnition of η for eventual algebraic simpliﬁcation.

The equation set (9.17)–(9.20) can now be written in terms of η and F(η). From

equations (9.24) and (9.25), we obtain

∂u

∂t

= U

∂F

∂t

= UF



∂η

∂t

=−UF



√

νt

3/2

=−



∂u

∂y

= U

∂F

∂y

= UF



∂η

∂y

= UF



√

νt

∂

∂y

√

νt



∂η

∂y

4νt



Here, a prime on F denotes derivative with respect to η. With these substitutions,

equation (9.17) reduces to the ordinary differential equation

−2ηF



= F



. (9.26)

The boundary conditions (9.18)–(9.20) reduce to

F(∞) = 0, (9.27)

F(0) = 1. (9.28)

Note that both (9.18) and (9.20) reduce to the same condition F(∞) = 0 . This is

expected because the original equation (9.17) was a partial differential equation and

needed two conditions in y and one condition in t. In contrast, (9.26) is a second-order

ordinary differential equation and needs only two boundary conditions.

Similarity Solution

Equation (9.26) can be integrated as follows:



=−2ηdη.

Integrating once, we obtain

ln F



=−η

+ const.

which can be written as

dη

= Ae

−η

310 Laminar Flow

where A is a constant of integration. Integrating again,

F(η) = A



−η

dη + B. (9.29)

Condition (9.28) gives

F(0) = 1 = A



−η

dη + B,

from which B = 1. Condition (9.27) gives

F(∞) = 0 = A



∞

−η

dη + 1 =

√

+ 1,

(where we have used the result of a standard deﬁnite integral), from which

A =−2/

√

π. Solution (9.29) then becomes

F = 1 −

√



−η

dη. (9.30)

The function

erf(η) ≡

√



−η

dη,

is called the “error function” and is tabulated in mathematical handbooks. Solution

(9.30) can then be written as

= 1 − erf



√

νt



. (9.31)

It is apparent that the solutions at different times all collapse into a single curve of

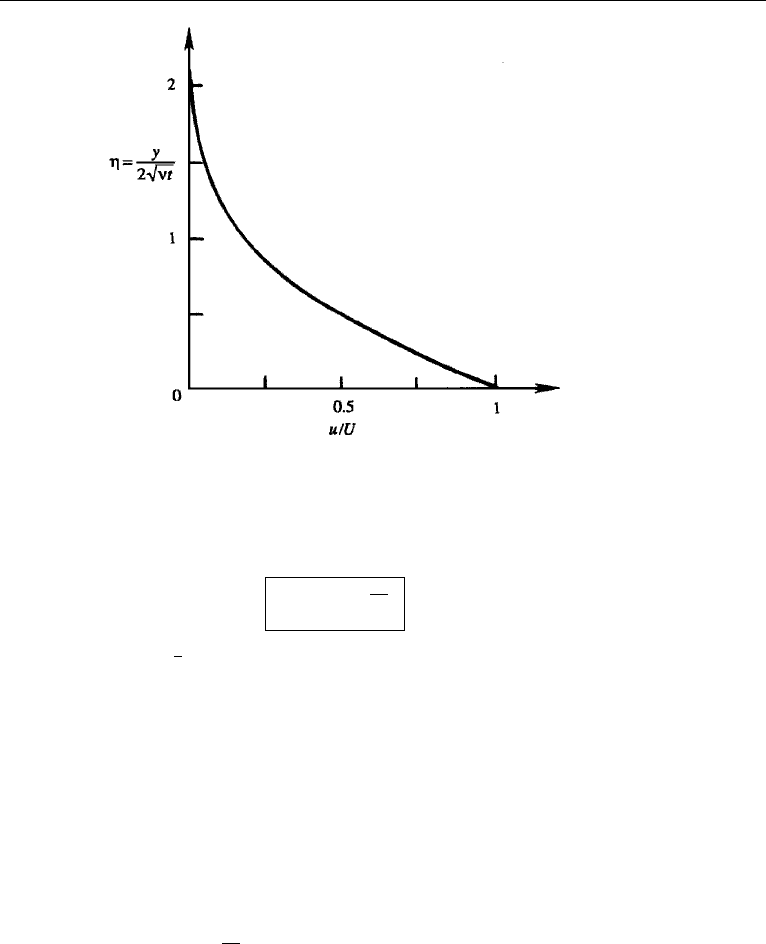
u/U vs η, shown in Figure 9.10.

The nature of the variation of u/U with y for various values of t is sketched in

Figure 9.9. The solution clearly has a diffusive nature. At t = 0, a vortex sheet (that

is, a velocity discontinuity) is created at the plate surface. The initial vorticity is in the

form of a delta function, which is inﬁnite at the plate surface and zero elsewhere. It can

be shown that the integral



∞

ωdy is independent of time (see the following section

for a demonstration), so that no new vorticity is generated after the initial time. The

initial vorticity is simply diffused outward, resulting in an increase in the width of

ﬂow. The situation is analogous to a heat conduction problem in a semi-inﬁnite solid

extending from y = 0toy =∞. Initially, the solid has a uniform temperature, and at

t = 0 the face y = 0 is suddenly brought to a different temperature. The temperature

distribution for this problem is given by an equation similar to equation (9.31).

We may arbitrarily deﬁne the thickness of the diffusive layer as the distance at

which u falls to 5% of U. From Figure 9.10, u/U = 0.05 corresponds to η = 1.38.

7. Impulsively Started Plate: Similarity Solutions 311

Figure 9.10 Similarity solution of laminar ﬂow due to an impulsively started ﬂat plate.

Therefore, in time t the diffusive effects propagate to a distance of order

δ ∼ 2.76

√

νt (9.32)

which increases as

√

t. Obviously, the factor of 2.76 in the preceding is somewhat

arbitrary and can be changed by choosing a different ratio of u/U as the deﬁnition

for the edge of the diffusive layer.

The present problem illustrates an important class of ﬂuid mechanical problems

that have similarity solutions. Because of the absence of suitable scales to render

the independent variables dimensionless, the only possibility was a combination of

variables that resulted in a reduction of independent variables (dimensionality of the

space) required to describe the problem. In this case the reduction was from two (y, t)

to one (η) so that the formulation reduced from a partial differential equation in y, t

to an ordinary differential equation in η.

The solutions at different times are self-similar in the sense that they all collapse

into a single curve if the velocity is scaled by U and y is scaled by the thickness of the

layer taken to be δ(t) = 2

√

νt. Similarity solutions exist in situations in which there

is no natural scale in the direction of similarity. In the present problem, solutions at

different t and y are similar because no length or time scales are imposed through

the boundary conditions. Similarity would be violated if, for example, the boundary

conditions are changed after a certain time t

, which introduces a time scale into the

problem. Likewise, if the ﬂow was bounded above by a parallel plate at y = b, there

could be no similarity solution.