Чорний О.П., Луговой А.В. и др. Моделювання електромеханічних систем
Подождите немного. Документ загружается.

рекомендацій тут дати не можна, оскільки точність методу
визначається видом функції, що підлягає інтерполяції,
розташуванням вузлів, вибором граничних умов та ін. і в
остаточному підсумку, визначається досвідом дослідника..
3.2.9.Інтерполяція функцій тригонометричними поліномами.
Нехай
(
)
fx періодична і задана на осі x
−
∞
<
<
+
∞
x
функція. Шляхом лінійної заміни незалежної змінної період
функції можна зробити рівним
π
=
2T . У цьому випадку
функцію доцільно інтерполювати тригонометричним поліномом
∑
=
++=
n
1k
kk0in
)kxsinbkxcosa(a)x(Q
так, щоб
)x(f)x(Q
iin
=
),n2,...,2,1,0i(
=
де
π
≤
≤
≤
≤
≤ 2x...xx0
n210
- точки з
[
)
π
2,0 . Поліном
будемо називати тригонометричним поліномом порядку
n .
Qx
n
()
Нехай
)x(fy
ii
=
)n2,...,2,1,0i(
=
. Необхідно підібрати
коефіцієнти полінома так, щоб виконувались наступні рівності
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎨
⎧
++=
++=
++=
∑
∑
∑
=
=
=
n
1k
n2kn2k0n2
n
1k
1k1k01
n
1k
0k0k00
)kxsinbkxcosa(ay
.................................................
)kxsinbkxcosa(ay
)kxsinbkxcosa(ay
Ми одержали систему рівнянь із
1n2
+
невідомими
. aabb ab
nn0 101
,,,,...,,
Як відомо, визначник цієї системи
75

∏
≤<≤
−
==∆
n2qp0
pq
n
n2n2n2n2
1111
0000
2
xx
sin2
nxsinnxcos...xsinxcos1
..................
nxsinnxcos...xsinxcos1
nxsinnxcos...xsinxcos1
2
і, отже, відмінний від нуля для нашої системи точок, для якої
π
<
−< 2xx0
pq
. Тому дана інтерполяційна задача має
розв'язок, причому єдиний. Таким чином, справедливим є
твердження, що тригонометричний поліном порядку n
однозначно визначається своїми значеннями в
1n2
+
неоднакових точках, розташованих на інтервалі
[
)
π
2,0 .
Для побудови поліному
візьмемо довільну точку x ,
що не збігається з вузлами
, і для цих
)x(Q
n
x
i
2n 2
+
точок складемо
систему з
22n
+
рівнянь:
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎧
=+−−
=+−−
=+−−
=+−−
∑
∑
∑
∑
=
=
=
=
n
1k
n2kn2k0n2
n
1k
1k1k01
n
1k
0k0k00
n
1k
k0k0n
0)kxsinbkxcosa(a)x(f
.................................................
0)kxsinbkxcosa(a)x(f
0)kxsinbkxcosa(a)x(f
0)kxsinbkxcosa(a)x(Q
,
лінійних і однорідних щодо коефіцієнтів С=1 при
, і , . . Ця система,
очевидно, має ненульовий розв'язок, і тому її визначник
дорівнює нулю, тобто
)x(Q
n
)x(f
k
a
k
b
k
)n2,...,2,1,0k( =
76
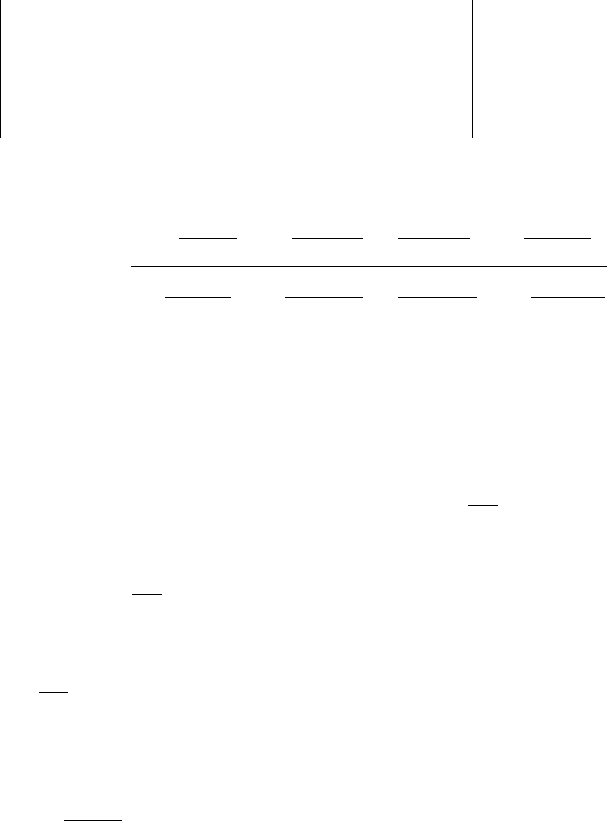
0
nxsinnxcos...xsinxcos1
..................
nxsinnxcos...xsinxcos1
nxsinnxcos...xsinxcos1
)x(f
...
)x(f
)x(Q
n2n2n2n2
000
n2
0
n
=
Розкладаючи його по елементах першого стовпця і розв'язуючи
його відносно
Q , після спрощення знаходимо: x
n
()
∑
=
+−
+−
−−−−
−
−
−
−
=
n2
0i
n2i1ii1ii0i
n21i1i0
in
2
xx
sin...
2
xx
sin
2
xx
sin...
2
xx
sin
2
xx
sin...
2
xx
sin
2
xx
sin...
2
xx
sin
)x(f)x(Q
Права частина формули - тригонометричний поліном порядку
, що задовольняє умовам. n
У випадках, коли
- періодична функція періоду )x(f
T
,
задана в точках
інтервалу xx x
n01 2
,,...,
(
)
Ta,a
+
( a - довільне
число), то за допомогою лінійного перетворення
()
ax
T
2
t −
π
=
одержуємо:
() ()
tt
T
2
afxf ϕ≡
⎟
⎠
⎞
⎜
⎝
⎛
π
+= ,
де
має період )t(ϕ
π
2 і задана в точках
)2,0[)ax(
T
2
t
ii
π∈−
π
= , . )n2,...,2,1,0i( =
У такий спосіб ми приходимо до розглянутого вище випадку.
Якщо точки інтерполяції
рівновіддалені,
тобто
(
xp n
p
= 01 2, ,...,
)
),n2,...,1,0p(,
1n2
p2
x
p
=
+
π
=
то інтерполяційному
поліному можна надати більш простий вигляд:
77
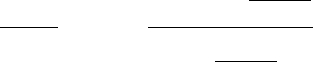
()
()
()
.
2
xx
sin
2
xx
1n2sin
xf
1n2
1
xQ
n2
0p
p
p
pn
∑
=
−
−
+
+
=
3.2.10. Апроксимація нелінійностей
Застосування методів інтерполяції функцій далеко не
вичерпує можливостей аналітичного подання функцій, заданих
таблично. Більше того, у деяких випадках застосування цих
методів неможливе взагалі, або є небажаним. Так, наприклад,
якщо число точок, у яких задана функція менше, ніж заданий
порядок полінома, то інтерполяція неможлива. Не можна
ігнорувати також і
той факт, що збіг у вузлах значень функції
може зовсім не означати, що характер її поведінки на інтервалі
інтерполяції також збігається. Вимога безумовної збіжності
значень у вузлах виглядає тим більше невиправданою, якщо
значення функції були отримані в результаті вимірів і є
сумнівними. У цих випадках доводиться використовувати інші
прийоми побудови
наближених функцій.
3.2.11. Метод найменших квадратів.
Як правило, у цих випадках використовують метод
найменших квадратів. Відповідно до цього методу як міру
відхилення поліному
m
m10m
xa...xaa)x(Q +++=
від заданої функції
y
f
x
=
() на множині точок
приймають величину
n10
x,...,x,x
[]
∑
=
−=
n
0i
2
iimm
)x(f)x(QS
,
що дорівнює сумі квадратів відхилень поліному від функції на
заданій множині точок.
Поліном, коефіцієнти якого
aa підібрані таким
чином, що величина
приймає найменше значення,
називається апроксимуючим поліномом.
a
m01
,,...,
S
m
78

Для розв'язання цієї задачі використовують загальний метод
диференційного зчислення, знаходячи часткові похідні від
величини
[
]
∑
=
−++++=
n
0i
2
i
m
im
2
i2i10m
yxa...xaxaaS
;
де
за всіма змінними . Прирівнюючи ці
змінні до нуля, одержуємо для визначення невідомих
систему
)x(fy
ii
= aa a
m01
,,...
aa a
m01
,,... 1m
+
рівнянь із 1m
+
невідомими:
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎨
⎧
=−++++=
∂
∂
=−++++=
∂
∂
=−++++=
∂
∂
∑
∑
∑
=
=
=
n
0i
i
m
i
m
im
2
i2i10
m
m
n
0i
ii
m
im
2
i2i10
1
m
n
0i
i
m
im
2
i2i10
0
m
0x]yxa...xaxaa[
a
S
2
1
.....................................................................
0x]yxa...xaxaa[
a
S
2
1
01]yxa...xaxaa[
a
S
2
1
Введемо позначення:
sxx x
k
kk
n
k
=
+
+
+
01
... ,..)2,1,0k(
=
,
txyxy xy
k
kk
n
k
n
=
+
+
+
00 11
... ,..)2,1,0k(
=
Перетворюючи систему і використовуючи введені позначення,
будемо мати
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=++++
=++++
=++++
++
+
mm2m2m21m1m0
11mm322110
0mm221100
tsa...sasasa
.............................................
tsa...sasasa
tsa...sasasa
де
. 1ns
0
+=
79

Можна показати, що коли серед точок немає
однакових і
n10
x,...,x,x
nm
≤
, то визначник системи відмінний від нуля, і
система має єдиний розв'язок:
.
m
*
m
1
*
1
0
*
0
aa,...,aa,aa ===
Якщо
nm
=
, то апроксимуючий поліном збігається з
поліномом Лагранжа для системи точок
, причому
.
Q
m
m10
x,...,x,x
0S
min
=
Таким чином, апроксимація функцій - це більш загальний
процес, ніж інтерполяція.
У загальному випадку, коли апроксимуючий поліном для
даної функції є узагальненим:
)x(c...)x(c)x(cQ
mm1100m
ϕ
+
+
ϕ
+
ϕ
= ,
то для обчислення його коефіцієнтів
слід
мінімізувати суму квадратів
m10
c,...,c,c
[]
∑
=
−ϕ++ϕ+ϕ=
n
0i
2
iimmi11i00m
,)x(f)x(c...)x(c)x(cS
де
- задана система точок. Використовуючи
необхідну умову екстремуму, одержуємо систему рівнянь:
xx x
n01
,,...,
() () () ()
[]
()
() () () ()
[]
()
() () () ()
[]
()
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎨
⎧
=ϕ−ϕ++ϕ+ϕ=
∂
∂
=ϕ−ϕ++ϕ+ϕ=
∂
∂
=ϕ−ϕ++ϕ+ϕ=
∂
∂
∑
∑
∑
=
=
=
n
0i
imiimmi11i00
m
m
n
0i
i1iimmi11i00
1
m
n
0i
i0iimmi11i00
0
m
0xxfxc...xcxc
c
S
2
1
...........................................................................................
0xxfxc...xcxc
c
S
2
1
0xxfxc...xcxc
c
S
2
1
Вводячи скорочені позначення
80
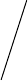
)x()x(),(
ii
n
0i
ψϕ=ψϕ
∑
=
,
систему приводимо до вигляду
⎪
⎪
⎩
⎪
⎪
⎨
⎧
ϕ=ψϕ++ψϕ+ψϕ
ϕ=ψϕ++ψϕ+ψϕ
ϕ=ψϕ++ψϕ+ψϕ
),f(),(c...),(c),(c
....................................................................
),f(),(c...),(c),(c
),f(),(c...),(c),(c
mmmmm11m00
11mm111100
00mm011000
З цієї системи знаходять коефіцієнти
. cc c
m01
,,...,
3.2.11. Апроксимація ортогональними функціями
Якщо степінь апроксимуючого полінома відносно велика,
то обчислення способом найменших квадратів стають
громіздкими. У цьому випадку іноді використовують метод
побудови апроксимуючого полінома, що базується на понятті
ортогональних функцій, тобто функцій, для яких на множині
точок
виконується умова: }x,...,x,x,x{X
n210
=
0)x()x(
i
n
0i
i
=ψϕ
∑
=
.
Якщо шуканий поліном у задачі апроксимації подати у
вигляді узагальненого полінома
)x(Pc...)x(Pc)x(Pc)x(Q
mm1100m
+
+
+
=
,
де поліном
)}x(P{
k
)m,...,2,1,0k(
=
ортогональний в системі
точок
, то коефіцієнти , що визначають
мінімум функції, можна обчислити за формулою:
X c
k
)m,...,2,1,0k( =
() ()
i
n
0i
k
2
i
n
0i
kik
xPxP)x(fc
∑∑
==
=
При цьому вибір системи ортогональних функцій - окрема
задача, виклад якої виходить за рамки даного підручника.
Приклад.
81

Розглянемо задачу фільтрації квазідетермінованого процесу
за результатами дискретних вимірів у відомі моменти
()
xt
tt t
N
01
, ,... . На вхід системи в зазначені моменти часу подається
сигнал
ν
ii
xp
i
=
+
, i
N
=
01,,..., , що складається з корисної
складової
xxt
ii
=
() й збурення ppt
ii
=
(). Приймемо, що на
інтервалі
процес може бути апроксимованим
поліномом
[, ]tt
N0
)t(x
)1m(
−
-го порядку з невідомими коефіцієнтами.
Відповідну апроксимацію виконаємо таким чином. Подамо на
вхід системи
xt xt
iN
() ( )
i
=
−
τ
, де
τ
iN
t
i
t
=
−
. Відповідно
до припущення про поліноміальну апроксимацію в околиці
точки, разкладемо у ряд Тейлора функцію
1m
iN
)1m(
1m
2
iNiNN
iNi
)t(x
)!1m(
)1(
...)t(x
2
1
)t(x)t(x
)t(x)t(x
−
−
−
τ
−
−
++τ+τ−=
=τ−=
Введемо до розгляду два
-мірних вектори: m
f
i
=(1,-
τ
i
, 0.5 ,...,
τ
i
2
()
()!
−
−
−
−
1
1
1
1
m
i
m
m
τ
)P
T
P
;
A =
−
(( ),
(),..., ())
(
xt xt x t
NN
m
N
1)
,
перший відомий, а другий, представлений сукупністю значень
сигналу
x
t
()
і
(m )
−
1
його початкових похідних у невідомий
момент
- невідомий. Тоді одержуємо t
N
x
i
=
fA
i
T
, і модель
вхідних даних набуває вигляду
vpi
ii
= N
+
=
fA
i
T
,,,...,12
Маючи в розпорядженні дискретні виміри, не можна точно
визначити процес
x
t
()
, якому вони відповідають, тому
необхідно за результатами спостережень відновити такий процес
у формі полінома
()
xt
i
(m )
−
1 -го порядку, який найменшим
82
чином віддалений від спостережень, тобто знайти оцінку
вектора
, що мінімізує функцію.
A
A
Іноді цей результат зручніше представити у більш
компактній формі. З цією метою введемо прямокутну (N+1) x m
- матрицю
, рядками якої є вектори-рядки i=0,...,N. З її
допомогою сукупність вимірів можна описати одним векторно-
матричним співвідношенням
F
f
i
T
VFAP=
+
, де і -
вектори вимірів і похибок вимірів.
V P
Оскільки
ff
ii
T
i
=
∑
FF
T
;
fv
ii
i
=
∑
FV
T
, то алгоритм
набуває еквівалентної форми
()
(
)
AV F F F V
TT
=
−1
.
Вираховуючи оцінку
(
)
AV , можна додатково вирішити
цілий ряд задач, пов'язаних із проблемою перетворення процесу
за деяким законом, загальний вигляд якого
h
H
A
T
=
. Тут -
відомий вектор, що визначає конкретний характер необхідного
перетворення процесу
H
x
t
()
- відновлення, екстраполяцію,
інтегрування, диференціювання, інтерполяцію і т.д. Очевидно,
що для виконання цього перетворення необхідно виконати
операцію скалярного множення раніш знайденого вектора
оцінок на вектор
. Виділимо ряд таких задач. H
T
Задача фільтрації. Знаходять оцінку значення процесу
x
t
() в момент tt
N
=
за спостереженнями. Оскільки
, то рішення задачі фільтрації зводиться до задачі,
розглянутої вище, якщо вважати
xf
NN
T
= A
H
T
=
(,,,...,)100 0
.
Задача екстраполяції. За спостереженнями необхідно
знайти оцінку
(
)
xt
N
+
τ
прогнозованого на час
τ
значення
процесу
x
t
().
83

Представимо
AH
T
=τ
−
−
+
+τ+τ+=τ+
−−
−
1m
N
)1m(
1m
2
NNNN
)t(x
)!1m(
)1(
...
...)t(x
2
1
)t(x)t(x)t(x
,
де
H
T
=
−
−
(, , ,...,
()
)1
1
21
2
1
ττ
!
τ
m
m
. Тоді відразу одержуємо
.
()
xt H A
N
T
+=τ
Задача інтерполяції. За спостереженнями необхідно знайти
оцінку
(xt
N
)
−
τ
процесу
x
t
() в момент tt
N
=
−
τ
.
Очевидно, що рішення зводитися до попереднього, якщо в
алгоритмі екстраполяції замінити
τ
на
−
τ
.
Задача диференціювання. Необхідно знайти оцінку
швидкості зміни процесу
x
t
()
в момент tt
N
=
за
спостереженнями. Беручи до уваги фізичний зміст компонентів
вектора
, що випливає з його визначення, представимо
, де
A
x
N
= HA
T
H
T
=
(,,...,)01 0
. Тоді шуканий розв'язок
можна знайти за вищевикладеною схемою:
.
xH
N
T
= A
t
Задача інтегрування. За спостереженнями необхідно знайти
оцінку
величини .
h
hxtd
t
N
=
∫
()
0
Представимо
()
(
)
[]
(
)
(
)( )
(
)
(
)
()
()
()
()( )
()
1m
NN
1m
1m
2
NNNNNNN
tttx
!1m
1
...
...tttx5.0tttxtxtttxtx
−
−
−
−
−
−
+
+−+−−=−−=
таким чином,
h
=
HA
T
,
84
