Чорний О.П., Луговой А.В. и др. Моделювання електромеханічних систем

Подождите немного. Документ загружается.

використовуючи які можна забезпечити достатню точність

моделювання при відповідному виборі кроку інтегрування. При

розв'язанні задач керування в реальному часі доцільно

використовувати економічний як за об’ємом використаної

пам’яті, так і за часом розв'язання метод Ейлера першого

порядку. Особливу актуальність це має при застосуванні в

мікропроцесорних системах керування електроприводами

Однак для більшості задач, моделі яких побудовані з

елементарних динамічних ланок, вибір кроку інтегрування може

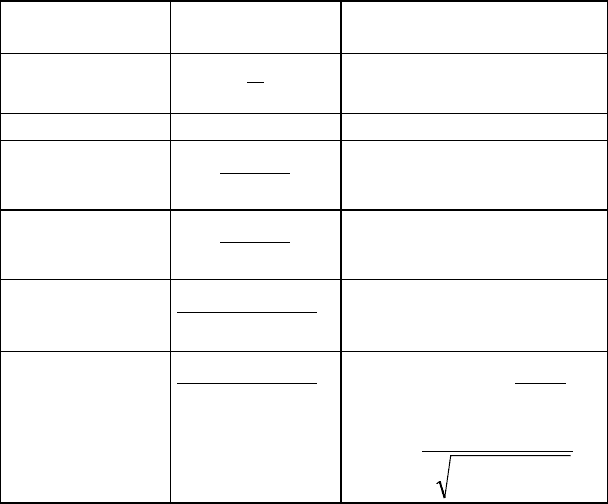
бути здійснений за таблицею 2.2.

Таблиця 2.2.

До вибору кроку інтегрування

Тип ланки Передаточна

функція

Значення

Інтегруюча

Диференціююча

Інтегро-

диференціююча

Аперіодична 1-

го порядку

Tp+

Аперіодична 2-

го порядку

Tp Tp++

01. , де

менша з

і T T

2 1

Коливальна

Tp Tp++

Менше з

()

−−

Таблиця 2.3.

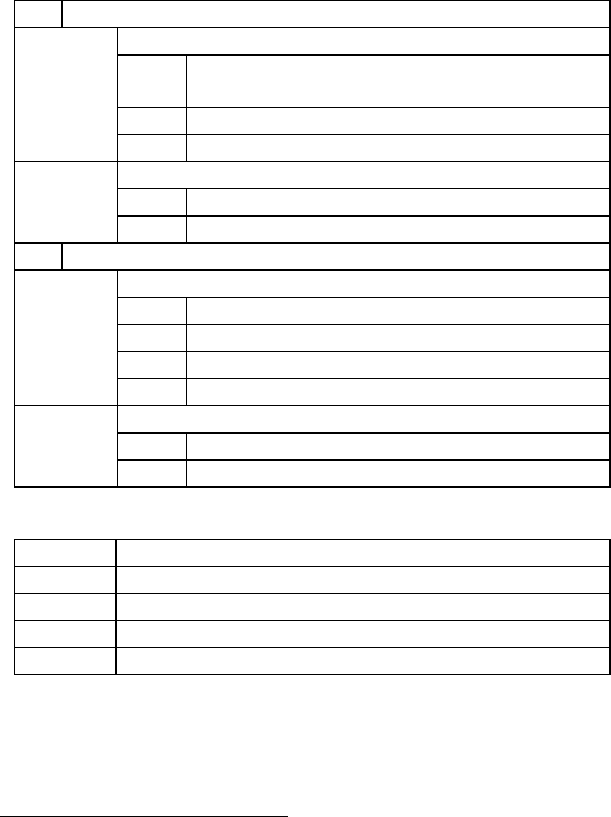
Методи розв'язання лінійних диференційних рівнянь, з порядком

вище першого

1 Однорідні рівняння

1.1 З постійними коефіцієнтами

1.1.1 Метод визначення коренів

характеристичного полінома

1.1.2 Метод перетворювання Лапласа

1.1.3 Ітераційний метод Пікара

1.2 Із змінними коефіцієнтами

1.2.1 Метод Форбеніуса

1.2.2 Ітераційний метод Пікара

2 Неоднорідні рівняння

2.1 З постійними коефіціентами

2.2.1 Метод невизначених коефіцієнтів

2.2.2 Метод перетворювання Лапласа або Фур'є

2.2.3 Метод варіації сталих

2.2.4 Ітераційний метод Пікара

2.2 Із змінними коефіцієнтами

2.2.1 Метод варіації сталих

2.2.2 Ітераційний метод Пікара

Таблиця 2.4.

Методи розв'язання нелінійних диференційних рівнянь

1 Ітераційний метод Пікара

2 Метод кусково-лінійної апроксимації

3 Метод збурень

4 Метод описуючих функцій

5 Метод фазової площини

PT Методи розв'язання диференційних рівнянь наведені в порядку

зростання складності їх використання

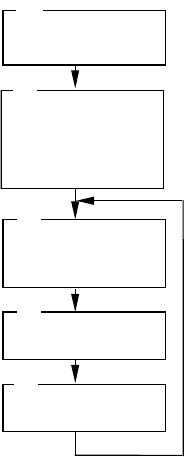
2.7. Типовий алгоритм і структура програми для

розв'язання систем диференційних рівнянь

Типова структура програми для розв'язання систем

диференційних рівнянь, незалежно

від використовуваного методу

інтегрування, складається з таких

основних блоків.

1. У блоці 1 здійснюється введення

з клавіатури або інших пристроїв

значень опорів, індуктивностей та

інших величин, що

використовуються як коефіцієнти

системи диференційних рівнянь.

2. У блоці 2 здійснюється введення

таких основних величин:

− початкові

умови системи

диференційних рівнянь;

− для нестаціонарної системи

диференційних рівнянь -

початковий час інтегрування;

− кінцевий час інтегрування;

− крок інтегрування.

3. Процедура обчислення правих

частин, як правило, підпрограма,

текст якої складає користувач.

Результатом роботи цієї підпрограми є обчислений масив

похідних шуканих функцій.

Введення

параметрів

процедури

інтегрування

Процедура

обчислення правих

частин С

Процедура

чисельного мето

ду

Процедура

вивод

даних

Введення

параметрів СДР

Рис.2.8. Алгоритм для

розв'язання системи

диференційних рівнянь

4. Процедура чисельного методу. Цей блок містить спеціальні

математичні формули, за

якими здійснюється розрахунок

чергової точки шуканих функцій. Тексти цих процедур є в

технічній літературі, найчастіше вони входять до складу

математичної бібліотеки, і користувач, як правило, їх не

розробляє.

5. Процедура виведення. Оскільки крок інтегрування дуже

малий, а кінцевий час

великий, то для зручності t

кні

сприйняття інформації на термінал або на друк виводяться не всі

точки, одержувані в процесі інтегрування, а, наприклад, кожна

десята. Частіше використовується така програмна конструкція,

коли дані направляються на пристрій виведення через деякий

визначений проміжок часу, що називається кроком друку

кратним кроку інтегрування.

др

При можливості варто використовувати виведення

інформації у вигляді графіків.

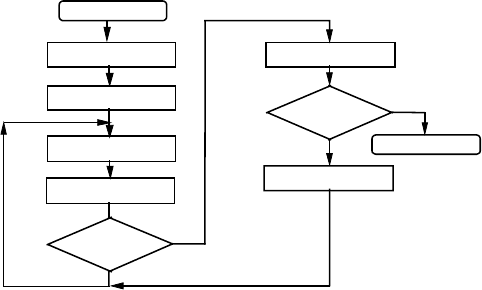
На рис.2.9. зображено узагальнений алгоритм програми

розв’язання системи диференційних рівнянь

=>i

др

i=i+1

кін

ні

зупинка

очаток

Рис.2.9. Узагальнений алгоритм програми розв'язання

системи диференційних рівнянь.

Розділ 3

Моделювання нелінійностей електромеханічних

систем

3.1. Основні нелінійності електромеханічних систем

При розгляді поведінки електромеханічних систем (ЕМС) у

перехідних режимах необхідно брати до уваги властиві їм

нелінійності.

Нелінійності в системах електропривода можуть бути

обумовлені такими чинниками:

1. Нелінійностями механічних характеристик електродвигунів

Наприклад: механічні характеристики асинхронних двигунів,

двигунів постійного струму послідовного і змішаного

збудження.

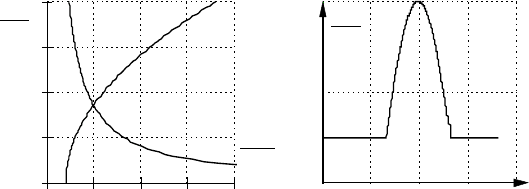
2. Нелінійностями характеристик навантаження (статичного

моменту).

0.25

0.5

0.75

0.5

−

> 1

а)

0 2 4 6

0.5

б)

Рис.3.1. Нелінійності обумовлені характеристиками

навантаження

Наприклад: вентиляторна характеристика турбомеханізмів

(

); характеристики металорізальних верстатів (α>1

−

рис.3.1,а); ножиці для різання металу (

(

)

=ϕ) рис.3.1,б).

3. Нелінійностями конструкції і властивостей механічної

передачі. Типовими прикладами є наявність у передачах

зазорів і люфтів, нелінійність характеристики з'єднання між

валами.

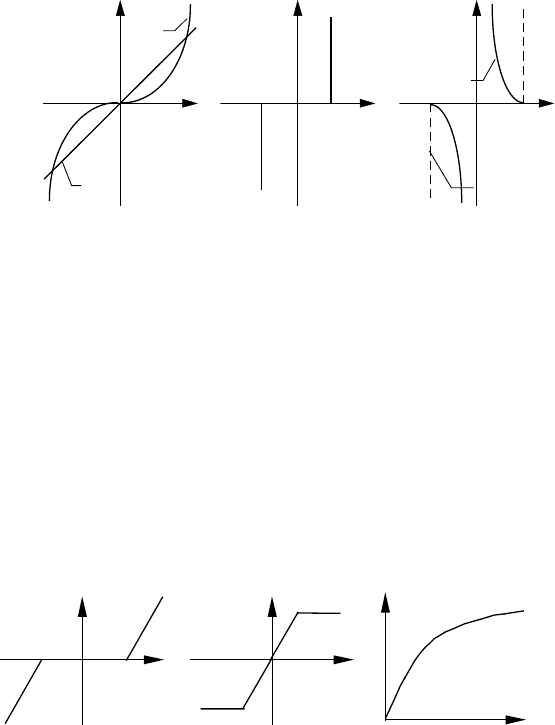
4. Нелінійності сил тертя.

а) внутрішнє в’язке тертя визначається силами, що діють у

підшипниках і з'єднаннях. Для підшипників ковзання в

діапазоні малих швидкостей

ω (рис.3.2.а) - 1); при

великих

більш точною є нелінійна залежність (рис.3.2.а) - 2); ω

а)

б)

в)

Рис.3.2. Нелінійні характеристики моментів тертя:

а) внутрішнє в’язке тертя; б) кулонівське тертя; в) сухе тертя.

Нелінійні гілки характеристик іноді приблизно заміняють

прямими (рис.3.2.а-в).

5. Нелінійності елементів системи керування електропривода.

До нелінійностей, що обумовлені елементами систем керування

електропривода відносять нелінійні елементи, за допомогою

яких здійснюється струмова відсічка в

замкнутих системах

автоматичного керування (САК) рис.3.3,а); елементи з

обмеженою величиною робочої ділянки робочої характеристики

- магнітні підсилювачі (МП), напівпровідникові суматори

(рис.3.3, б); елементи, що мають область насичення (рис.3.3, в)

та ін.

ви

вх

а)

вих

вх

б)

вих

вх

в)

Рис.3.3. Нелінійності елементів систем керування

електропривода

6. Нелінійності функціональних впливів.

Нелінійності типу добутку двох функцій, квантування за

рівнем і часом у цифрових САК.

7. Нелінійностями, обумовленими властивостями

перетворювачів електричної енергії, наприклад,

нелінійностями регулювальної

характеристики

(

)

вхвих

UfU

тиристорного

перетворювача (рис.3.4.); наявністю зони

переривчастих струмів; неповною керованістю

перетворювачів та ін.

Розглянуті нелінійності є основними, але не

вичерпують усієї різноманітності нелінійностей.

Електромеханічна система може мати відразу

декілька нелінійностей, і необхідно виділити

найбільш важливі, що суттєво впливають на

показники роботи досліджуваного об'єкта.

Нелінійності можна поділити на дві групи:

- аналітичні-

такі, що можуть бути

представлені системою кусково-неперервних рівнянь.

ви

Рис.3.4.

Нелінійність

регулювальної

характеристики

- неаналітичні-такі,що представлені у вигляді графіків або

таблиць.

До першої групи належать:

1. Нелінійність типу "обмеження".

Нелінійність може бути описана такою

системою рівнянь:

вих

−U

вх

Рис.3.5.

Нелінійність типу

«обмеження»

()

U якщо UU

UUsignUякщо UU

вих вх вх

=⋅ ≤

=⋅ >

⎧

⎨

⎪

⎩

⎪

де

- знакова функція. sign

2. Нелінійність типу "ідеальне реле"

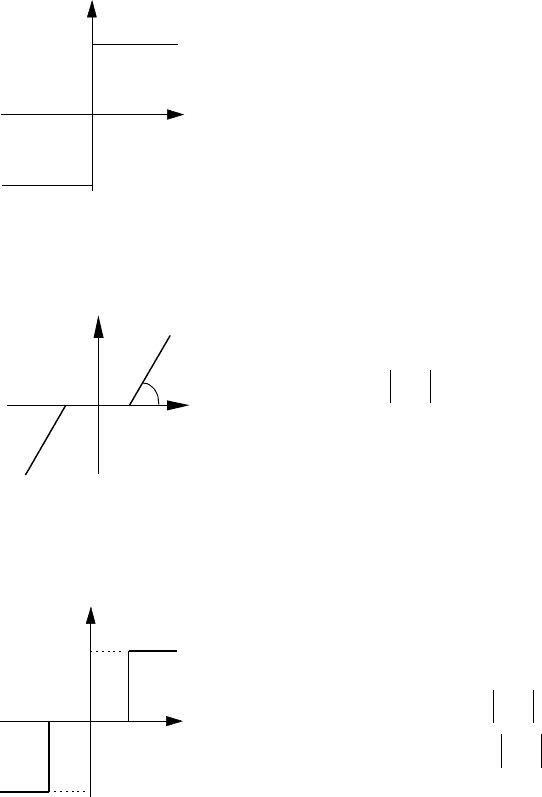
Нелінійність може бути описана такою

системою рівнянь:

U якщо U

вих

вх

−≤

⎧

⎨

⎩

або

(

)

UUsignU

вих вх

=⋅

3. Нелінійність типу "зона

нечуттєвості"

вих

−U

вх

Рис.3.6.

Нелінійність типу

«ідеальне реле»

Нелінійність може бути описана такою

системою рівнянь:

()

U якщо UU

UaUUякщо UU

вих вх

вих вх вх

=≤

=− >

=+ <−

⎧

⎨

⎪

⎩

⎪

де

atg

4. Нелінійність типу "реальне реле" або "реле з зоною

нечуттєвості"

вих

−U

вх

Рис.3.7. Нелінійність

типу «зона

нечуттєвості»

Нелінійність типу "реальне реле" або "реле з

зоною нечуттєвості" може бути описана

такою системою рівнянь:

()

U якщо UU

UUsignUякщо UU

вих вх

вих вх вх

=≤

=⋅ >

⎧

⎨

⎪

⎩

⎪

вих

−U

вх

Рис.3.8.

Нелінійність типу

«реальне реле»

5. Нелінійність типу "прямокутна петля гістерезиса"

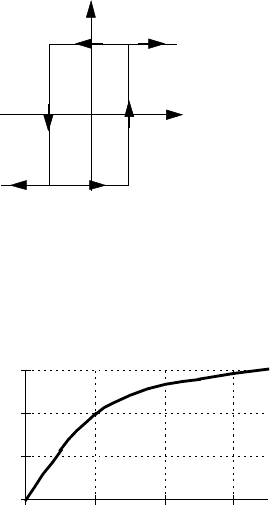
Нелінійність може бути описана такою

системою рівнянь:

вих

−

−U

вх

Рис.3.9.

Нелінійність типу

«реальне реле»

U якщо UU

UUякщо UUи U

вих вх

вих вх вх

=>−

=− < >

⎧

⎨

⎪

⎩

⎪

∆

З наведених прикладів опису видно, що

нелінійності подаються у вигляді сукупності

операторів присвоювання і логічних функцій.

Неаналітичні нелінійності - такі, що не

можуть бути описані аналітичними виразами.

До другої групи відносяться нелінійності обумовлені

кривими намагнічування, вольт-амперними характеристиками

нелінійних опорів тощо

Типовим, широко поширеним

прикладом такої нелінійності є

крива намагнічування (рис.3.10.).

Початкова ділянка - це практично

пряма лінія, далі - крива.

0,5

1,5

0123

i во

зб

,..

о,..

Рис.3.10. Нелінійна крива

намагнічування

Існує два основних методи

моделювання нелінійностей

заданих таблицями та графіками:

інтерполяція та апроксимація.

Інтерполяція. Нелінійність задається у вигляді таблиці

значень у дискретних точках, а значення функції в проміжних

точках можуть бути знайдені за допомогою різних

інтерполяційних алгоритмів, наприклад, методи Лагранжа,

Ньютона, Стірлінга й

ін.

Апроксимація. За допомогою відомих чисельних методів

(наприклад - найменших квадратів) підбирається аналітичний

вираз для нелінійності. Апроксимація функцій це більш

загальний процес, ніж інтерполяція, тому у деяких випадках

отримати простий аналітичний вираз нелегко. У таблиці 3.2.

наведені приклади апроксимації нормованої кривої

намагнічування, що задана таблицею 3.1.

Таблиця 3.1.

Нормована крива намагнічування

i , в.о. 0.5 1.0 1.5 2.0 2.5 3.0 3.5

E , в.о. 0.58 1.0 1.21 1.33 1.4 1.46 1.51

Таблиця 3.2.

Параметри апроксимуючої функції кривої намагнічення

1. E

ab ci

зб

⋅+⋅

помилка

=0.0161842, коефіцієнт кореляції ,

=0.9997536

-0.0006763 0.6830981 1.6691347 1.4405316 -

2. , Eabi ci di ei

зб зб зб зб

=+⋅+⋅+⋅+⋅

234

помилка

=0.0083557, коефіцієнт кореляції ,

=0.9999179

-0.0066045 1.5009997 -0.6301088 0.1269412 -0.0097902

(

)

Ea e

зб

=−

⋅

1 ,

помилка

=0.0174020, коефіцієнт кореляції ,

=0.9995014

1.5497733 0.99040697 - - -

(

)

Eabe

зб

=−

⋅

помилка

=0.0186582, коефіцієнт кореляції ,

=0.9995087

1.5541374 0.9965776 0.9952512 - -

abi

ci di

зб

зб зб

⋅

+⋅ + ⋅1

помилка

=0.0237487, коефіцієнт кореляції ,

=0.9993367

-0.0065968 1.6224211 0.6113947 0.0514903 -