Чорний О.П., Луговой А.В. и др. Моделювання електромеханічних систем
Подождите немного. Документ загружается.

Σ
1
p
1
p
×
×
-a
0
-
a
0
x
-a
1
-
a
1
x
′
x
x
′
x
″
y
=
ƒ
(
t)
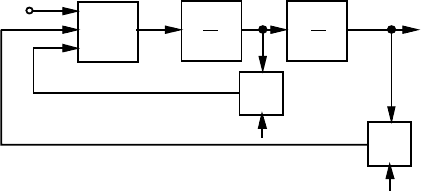
Рис.2.7. Структурна схема розв'язання диференційного рівняння.
2.4. Точність і похибка отриманих рішень
При моделюванні на АОМ постає питання про точність
рішень. Основна величина похибки вноситься вирішуючими
елементами.
Основні види похибок вирішуючих елементів:
1. Похибка, внесена скінченним значенням коефіцієнтів
підсилення ОП.
Отримані вище вирази для передатної функції ОП отримані в
припущенні, що коефіцієнт передачі ОП нескінченно великий,
оскільки коефіцієнт підсилення ОП має скінченну величину,
то
він виконує всі операції з деякою похибкою, яка тим більша, чим
менший коефіцієнт підсилення.
2. Похибка опору кіл зворотних зв'язків (ЗЗ) і вхідних.
Вона визначається неточністю номінативних значень елементів,
витоками конденсаторів і т.п.
3. Похибка зумовлена нестабільністю нульового рівня
підсилювачів.
Дрейф нуля ОП зумовлений нестабільністю живлячої напруги,
зміною параметрів
ОП при нагріванні і т.п. Для зменшення
впливу дрейфу нуля перед кожним запуском моделі
здійснюється установлення нулів ОП. Також необхідно
обмежувати час роботи електронної моделі на рівні 20 - 30 с.
4. Похибка нелінійних диференційних перетворень.
46
У загальному суматорі похибка внесена вирішуючими
елементами, знаходиться на рівні декількох відсотків, що для
більшості технічних рішень є цілком прийнятним.
2.5. Моделювання на АОМ систем з оптимізаційними
контурами
1. Загальні методи розв'язання задач оптимізації.
Система, для якої показник якості має екстремальне
значення, називається оптимальною.
Параметри системи, при яких забезпечується оптимальний
процес чи стан, тобто екстремальне значення показника якості,
називаються оптимальними. Відшукання оптимальних
параметрів системи - мета задачі оптимізації.
Задачі оптимізації поділяються на детерміновані і
ймовірнісні - стохастичні.
Детерміновані задачі характеризуються
тим, що критерій
оптимальності є детермінованою функцією параметрів, що
оптимізуються.
Ймовірнісні задачі характеризуються наявністю випадкових
процесів.
При виборі методу розв'язання необхідно враховувати
відсутність або наявність обмежень на параметри або стани, що
оптимізуються. Задачі без обмежень більш прості (добре відомі).
Задачі з обмеженнями належать до задач математичного
програмування.
При цьому складність
задачі значною мірою визначається
видом критерію оптимальності й обмежень. Якщо вони лінійні,
то задача - з області лінійного програмування, якщо нелінійні -
нелінійного програмування.
За числом екстремумів задачі бувають одно- і
багатоекстремальні.
За числом оптимізаційних параметрів задачі поділяють на
одномірні і багатомірні.
АОМ загального призначення придатні для розв'язання
задач оптимізації динамічних
систем, що описуються
47

звичайними диференційними рівняннями без обмежень. Такі
задачі належать до класу варіаційних і крайових задач із
звичайними похідними.
2. Крайові і варіаційні задачі
При вирішенні технічних проблем виникають задачі
оптимізації динамічних властивостей системи. Вони в багатьох
випадках приводять до розв'язання диференційного рівняння
()
dx
dt
fx x t
i
in
= ,..., , , in
=
1,..., (2.16)
з крайовими умовами
(
)
(
)
(
)
(
)
[]
H Fxt xt xt xt
ll n k nk
==
11 2 1
0,..., ,..., ,..., ,
(2.17) l= 1,...,m
де
(
)
(
)
tt t xt xt
n12 11
, ,..., ; ,...,
nk
- задані фіксовані значення
незалежних змінних і відповідні значення залежних змінних.
Завдання ідентифікації полягають у визначенні параметрів
або виду правих частин рівнянь системи, щоб задовольнити
умовам більш загального виду:
()
(
)
(
)
[]
Fx t x t x t a a a
lnnk m11 12
0,..., ,..., , , ,..., =
, lm
=
1,..., (2.17)
де
- задані функціонали, що поширюються на весь інтервал
інтегрування;
F
l
(
)
(
)
xt xt
nk11
,..., - функції, що є рішенням
первинної системи диференційних рівнянь;
-
параметри, що повинні бути визначені для виконання заданої
умови.
aa a
m12
,,...,
Для задачі оптимізації параметри системи повинні бути
вибрані так, щоб рішення її перетворювало в мінімум або
максимум деякий функціонал
()
(
)
(
)
[
]
Fx t x t x t
lnn11
,..., ,...,
k
, що
у цьому випадку називається критерієм оптимальності.
Майже всі існуючі методи вимагають багатократного
розв'язання задачі Коші для різних значень початкових умов або
параметрів системи. Процес розв'язання зводиться до пошуку
48

необхідних значень, і методи розв'язання називаються
пошуковими. До них належать:
1. метод проб;
2. метод комбінацій;
3. метод близькості рішень;
4. метод огляду;
5. метод покоординатної мінімізації;
6. метод градіента;
7. метод найскорішого спуску.
Метод проб - застосовується для розв'язання крайових і
варіаційних задач. Спочатку знаходиться пробне рішення при
довільних початкових умовах. Для
кожного варіанту оцінюється
близькість одержуваного рішення до потрібного.
Метод комбінацій - використовується для розв'язання задач,
що описуються лінійними диференціальними рівняннями.
Зводиться до рішення
допоміжних задач Коші з наступним
розв'язком системи лінійних алгебраїчних рівнянь відносно
початкових умов, що повинні бути знайдені.
n
Метод огляду характеризується зміною параметрів за
визначеною програмою, що не враховує результатів попередньго
рішення. Здійснюється рівномірне сканування з постійним
кроком в діапазоні допустимих значень параметрів. Недоліки:
− велика кількість пробних розв'язків,
−
великий час дослідженнь.
Метод покоординатної мінімізації передбачає зміну по черзі
кожного елемента вектора
Y
при фіксованих значеннях інших
елементів із переходом до зміни наступного параметра при
досягненні часткового екстремуму залежності функціонала
µ
осі змінюваного параметра, коли
∂
µ
∂
y
i
= 0 .
Після циклу пошуку за всіма m параметрами знову
починається зміна першого параметра, і цикл повторюється.
Пошук продовжується, поки всі часткові похідні
∂
µ
∂
y
i
не стануть
близькими до 0.
49
Метод градіента передбачає одночасну зміну всіх шуканих
параметрів і характеризується необхідністю знаходження
пробних рішень для визначення напрямку вектора градіента.
Метод найскорішого спуску - це варіант методу градіента.
Завдяки великій швидкості рішення задач на АОМ можна за
короткий час дослідити багато варіантів рішення задачі Коши з
різними початковими умовами і вибрати той, що
задовольняє
граничним умовам або умовам оптимізації.
2.6. Чисельні методи розв'язання систем диференційних
рівнянь на ЦОМ
Практично всі задачі, що виникають при моделюванні
електроприводів, зводяться до розв'язання систем нелінійних
диференційних рівнянь. Математичний апарат для аналітичного
розв'язання таких задач або занадто громіздкий або відсутній. За
цих умова єдиним виходом є застосування чисельних методів
інтегрування систем диференційних рівнянь.
Розв'язання систем нелінійних диференційних рівнянь
полягає у знаходженні
залежностей
(
)
yt
i
при відомих
початкових умовах
tt
=
0
(початковий час) і yy
it
00
=
(початкові значення змінних системи).
Усі відомі чисельні методи розв'язання систем
диференційних рівнянь поділяються на два класи - однокрокові і
багатокрокові. Реалізація однокрокових методів полягає в
розкладанні шуканої функції в ряд Тейлора, у якому
утримується те, чи інше число членів, що визначає порядок
методу
N
. При однокрокових методах розв'язку кожне нове
значення знаходиться за одним відомим попереднім
значенням
. Як приклад реалізації однокрокового методу
наведемо найпростіший метод Ейлера першого порядку:
y
i +1
y
i
(
)
yyhFty
ii i+
=+
1
,
i
, (2.18)
де
- крок інтегрування. h
50

Суть даного методу полягає в заміні інтегральної кривої на
кожному кроці інтегрування відрізком прямої.
Більш складним, але й більш точним є метод Рунге - Кута 4-
го порядку, що задається такими формулами:
()
()
khFtY
khFt
h
Yk
khFt
h
Yk
khFthYk
Y
kkkk
ii
ii
ii
ii
i
1
21
3
43
1
1234
2
1
2
2
1
2
22
2
6
=
=++
⎛
⎝
⎜
⎞
⎠
⎟
=++
⎛
⎝
⎜
⎞
⎠
⎟
=++
=
+++
+
,;
,;
,
,;
.
;
(2.19)
Таким чином, при використанні методу Рунге-Кута 4-го
порядку необхідно зробити чотири обчислення правих частин
системи диференційних рівнянь. Тому час обчислень для цього
методу істотно зростає, але точність істотно вища.
Однокроковим методам притаманна властивість
"самостартування", а також є порівняно проста можливість
зміни кроку інтегрування в процесі обчислень.
Реалізація багатокрокових
методів полягає в тому, що в них
за рядом попередніх значень
(
)
yt , обчислюється визначене
значення функції. Порядок методу дорівнює числу
використовуваних попередніх значень функції. До даної групи
методів належать: група методів Адамса, метод Мілна, метод
Хемінга, група методів прогнозу і корекції.
Існуючі методи чисельного інтегрування диференційних
рівнянь можна класифікувати як явні і неявні; - одно- та
багатокрокові (табл.2.1), де
(
)
(
)
yf
1
,
1
- значення змінної та її
похідної після першого циклу розрахунку;
(
)
(
)
yf
ν
,
ν
- значення
змінної та її похідної після
ν
-ї ітерації; Я - явний метод; Н -
неявний; О- однокроковий; Б - багатокроковий; ПК - прогнозу та
корекції.
51

Важливою перевагою багатокрокових методів є той факт,
що для обчислення чергового значення інтегральної кривої
потрібне тільки одне обчислення правих частин системи
диференційних рівнянь, що помітно прискорює розрахунок.
Однак цей метод позбавлений можливості "самостартування"
через відсутність попередніх значень. Для відшукання цих
значень і запуску процедури багатокрокового методу необхідно
використовувати один із
наявних однокрокових методів.
За допомогою явних однокрокових методів значення змінної на
-му кроці інтегрування визначається тільки на основі
інформації про значення змінної та її похідної на попередньому
кроці розрахунку.
i + 1
Неявні методи інтегрування використовують багатократне
ітераційне уточнення змінної на кожному кроці інтегрування.
Ітерації виконують, доки не буде досягнута необхідна похибка
обчислень
(
)
yy
iiнеобх+
+
+
−<
1
1
1
ν
ν
δ
.
, (2.20)
або кількість ітерацій не перевищить максимальне задане число
. ν
max
Похибка методу чисельного інтегрування визначається
двома складовими: похибкою округлення та похибкою
апроксимації.
52

Талиця 2.1.
Класифікація чисельних методів інтегрування диференційних рівнянь
№
п/п
Метод Порядо
к
методу
Формула чисельного інтегрування Вид
методу
Кільк.
ітерацій
Локальна
похибка
1. Ейлера 1
yyf
iii+
h
=
+
1
ЯО 1
h
2
2. Модифі-
кований
Ейлера
2
(
)
yy
iii+
=+
1
1
hf
;
(
)
(
)
yy hff
ii ii++
=+ +
11
1
05.
,
де
(
)()
()
()
ffyu
ii
i
++
+
=
1
1
1
1
1
,
ЯО 2
h
3
3. Рунге-
Кута
4
()
4321i1i
kk2k2k6/hyy ++++=
+
,
де
;
()
kfyu
ii1
= ,
(
)
kfy hku
ii2105
05=+
+
.,
.
;
()
kfy hku
ii3205
05=+
+
.,
.
;
(
)
kfyhku
ii431
=+
+
,
ЯО 4
h
5
4. Неявний
Ейлера
1
()
yyhfyu
ii i+
+
++
=+
1
1
11
νννν
,
i
НО
≥2
h
2
5. Адамса-
Бешфор-
та
2
(
)
(
)
[]
yy hfyufyu
ii ii ii+−
=+ −
11
05 3., ,
−1
;
(
)
[]
24/f9f37f59f55hyy
3i2i1iii
1
1i −−−+
−+−+=
ЯБ 1
h
3
6. Адамса-
Мултона
4
(
)
(
)
(
)
()
yfyu
iii+++
=
1
1
1
1
1
1
,
;
(
)
[]
yy
h
ffff
ii i iii++−−
=+ + − +
11
1
12
24
9195
ЯБ,ПК 4
h
5
53
54

Похибка округлення зростає пропорційно . Для
зменьшення цієї складової похибки слід збільшити крок
інтегрування, але при цьому починає зростати похибка
апроксимації, яка прямо пропорційна кроку
. Через вказані
причини можливе нестійке розв'язання для стійкого процесу.
1/ h
h
Порядок величин локальних похибок апроксимації наведено
в табл.2.1. На основі інформації про локальні похибки можна
порівнювати різні алгоритми широкого класу задач, в тому числі
і нелінійних, для яких точний аналітичний розв'язок отримати
неможливо. Таким чином, слід говорити про необхідність
оптимального вибору кроку інтегрування.
Верхня межа кроку інтегрування може бути визначена
згідно з теоремою Котельникова-Шеннона:
h ≤
1
2ω
max
, (2.21)
де
- максимальна частота спектра досліджуваного процесу
за умови, що значення кроку інтегрування задовольняє умови
стійкості обраного чисельного методу.
ω
max
Для отримання стійкого розв'язання за умови, що
досліджувана система є стійкою, а значить усі корені
(
i ) характеристичного рівняння замкнутої системи
знаходяться в лівій площині, необхідно і достатньо, щоб
значення були
p
i
n= 1,...,
λ
ii
hp
=
(in
=
1,..., ) розташовані усередині
області стійкості даного чисельного методу. Однак
розташування всіх
λ
i
в межах області стійкості не гарантує
інколи отримання задовільного результату, а дійсна область
стійкості виявляється значно меншою.
Таким чином, одночасно із загальновизнаними точними
методами чисельного інтегрування високого порядку, наприклад
Рунге-Кута четвертого порядку, Кута-Мерсона четвертого
порядку, на основі яких розроблені стандартні програми
чисельного інтегрування рівнянь з постійним та змінним
кроком
інтегрування, доцільно використовувати при розробці
нестандартних методик моделювання менш точні методи,
наприклад Ейлера другого порядку і Адамса-Бешфорта,
55
