Чорний О.П., Луговой А.В. и др. Моделювання електромеханічних систем
Подождите немного. Документ загружается.


.
j,
1
*
ωβλλ
±−=
Таким чином, запис передатної функції у вигляді добутку
дробів (1.12) можна розглядати як ще одне аналітичне
представлення системи, показаної на рис. 1.4,в, але у вигляді
послідовно з'єднаних елементарних ланок.
Передатну функцію (1.11) у випадку дійсних різних коренів
можна звести до вигляду:
,
pa
b
p
1
a
b
)p(W
n
1i
i
i
n
0
n
1i
in
0
∑
∏
=
=
−
=
−
=
λ
β
λ
(1.23)
що відповідає паралельному з'єднанню елементарних ланок виду
()
i
p
1
λ
−
(рис.1.6,а). Коефіцієнти
i
β
знаходять як різницю
функції комплексної змінної W(p) у полюсах або розраховують
методом невизначених коефіцієнтів.
Така модель безпосередньо відповідає аналітичному запису
загального рішення як лінійної комбінації часткових рішень,
обумовлених коренями характеристичного рівняння у вигляді:
,ec)t(y
n
1i
t
i
i
∑
=
=
λ
(1.24)
де
- коефіцієнти, що розраховуються за початковими
умовами. Ця модель зручна для графоаналітичного розрахунку
перехідної характеристики системи як суми перехідних
характеристик типових ланок, що входять до її складу.
i
c
26
b
n
x
n
(
)
yt
()
ut
x
1
b
1
1
p
λ
1
1
p
λ
n
d
a
n
0
а)
x
p
()
ut
c
1
a
1
1
p
d
a
n
0
1
p
c
2
a
0
(-) (-)
б)
x
j
()
ut
c
1
λ
1
1
p
d
a
n
0
1
p
c
q
λ
i
q-раз
(-) (-)
в)
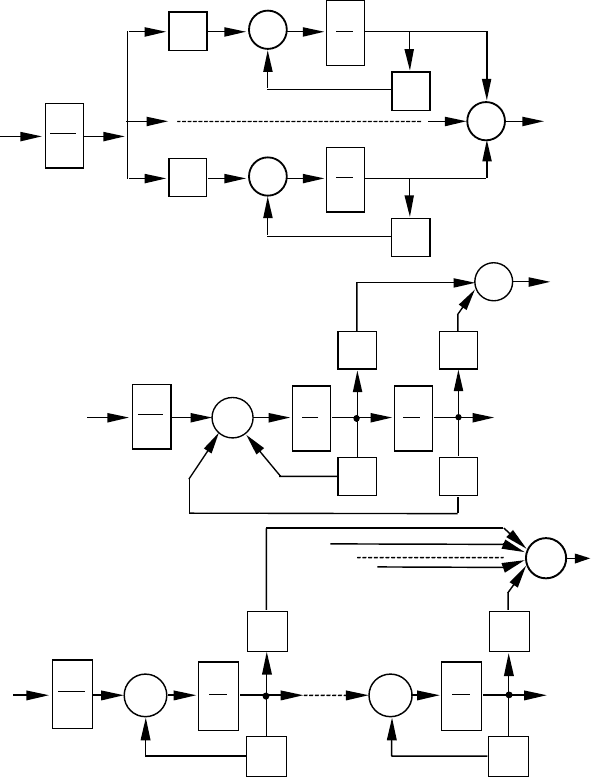
Рис.1.6. Структурні моделі системи у вигляді паралельного
з'єднання елементарних аперіодичних ланок (а); коливальної
ланки (б) та для кратних коренів (в) у її складі.
27
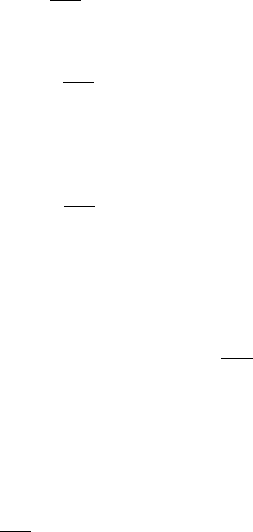
За структурною моделлю на рис.1.6,а легко записати
систему диференційних рівнянь першого порядку:
),()()(
.........................................
);()()(
);()()(
0
0
2222
0
1111
tu
a
d
btxtx
tu
a
d
btxtx
tu
a
d
btxtx
n
nnnn
n
n
+=
+=
+=
λ
λ
λ
(1.25)
яку також можна представити в розгорнутій матричній формі:
),(
)(
)(
)(
00
00
00
)(
)(
)(
1
0
2
1
2
1
2
1
tu
b
b
b
a
d
tx
tx
tx
tx
tx
tx
n
n
n
nnn
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
+
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
…
…
λ
λ
λ
(1.26)
або, більш компактно, у вигляді:
),()()(
0
tub
a
d
txtx
n
+∆=
(1.27)
де
)
t
(
x
n-мірний вектор стану динамічної системи,
∆
-
діагональна матриця власних значень розміром
nn
×
, b
- п-
мірний вектор керування. Матриця
∆
зв'язана з матрицею A
співвідношенням:
AP
P
1−
=∆ , (1.28)
де
P
- матриця Вандермонда, вектор A
)
t
(
x
зв'язаний із
вектором
)
t
(
z
співвідношенням (1.29).
)t(zP)t(x
1
−
=
. (1.29)
28
Таким чином, структурна модель на рис.1.6,а відповідає
канонічній формі (1.26) і (1.27) аналітичного представлення
математичної моделі системи з дійсними різними коренями
характеристичного рівняння. За наявності комплексно-
спряжених коренів до цієї моделі необхідно додати коливальні
ланки, вид структури яких показаний на рис1.6,б. У випадку
кратних дійсних коренів можна використовувати структурну
модель
, показану на рис.1.6,в. Коефіцієнти для цих моделей
найзручніше розрахувати методом невизначених коефіцієнтів. У
матриці
i
c
∆
коливальним ланкам відповідають елементи виду:
βω
ωβ
−−
−
1
1
Для системи з передатною функцією загального виду
01
1n
1n
n
n
01
1m
1m
m
m
n
0i
i
i
m
0k
k
k
apapapa
bpbpbpb
pa
pb
)p(W
++++
++++
==
−
−
−
−
=
=
∑
∑
…
…
(1.30)
запишемо зображення Лапласа вихідної
(
)
yp
як
).p(u
pa
1
pb)p(y
n
0i
i
i
k
m
0k
k
∑
∑
=
=
=
(1.31)
Введемо додаткову змінну
(
)
Zp
у вигляді
),p(u
pa
1
)p(Z
n
0i
i
i
∑
=
=
(1.32)
передатна функція для якої
()
(
)
()
pu
pZ
pW =
збігається з
передатною функцією (1.4) при
1b
0
=
Для зручності
29
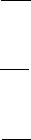
зіставлення структурна модель рис.1.4,в відтворена на рис.1.7,а
при
. Із співвідношень (1.31) і (1.32) можна записати: 1b
0
=
),p(Zpb)p(y
k
m
1k
k
∑
=
= (1.33)
звідкіля випливає, що
(
)
yp можна одержати додаванням
змінних стану з виходів інтеграторів, помножених на відповідні
коефіцієнти від
до при
0
b
1n
b
−
mn
=
, і вищої похідної
, помноженої на коефіцієнт (рис.1.7,б). Якщо
, то коефіцієнти
)t(Zp
n
n
b
mn< 0b
k
=
для всіх
k
m> .
У такому вигляді
-мірний інтегратор із матрицею
зворотного зв'язку і
-мірним суматором на вході (рис.1.4,г), як
і раніше, моделює перетворення скалярного входу u(t) у вектор
стану системи
n
n
)t(Z
. а сукупність коефіцієнтів і суматор 2 на
рис.1.7,б представляють блок С структури на рис.1.4.г, що
перетворює вектор стану
i
b
)t(Z
у скалярний вихідний сигнал
)
t
(
y таким чином, щоб залежність останнього від вхідного
сигналу u(t) задовольняла диференційному рівнянню загального
виду (1.1). Інший варіант структурної моделі для системи
загального вигляду (1.1) показаний на рис.1.8. Коефіцієнти
k
β
цієї моделі розраховують за формулами:
()
()
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎬
⎫
−−=
−=
=
−−−
−−
…………………………………
;aab
a
1
;ab
a
1
;b
a
1
1n11n02n
n
2
1n01n
n
1
n
n
0
βββ
ββ
β
(1.34)
30
)p(zp
n
)p(zp
2n−
)p(zp
1n−
)p(z
)p(pz
)p(u
n
a
1
1n
a
− 2n
a
−
1
a
0
a
p
1
p
1
p
1
p
1
(-)
zp
n
zp
2n−
zp
1n−
)p(z
pz
)p(u
n
a
1
1n
a
− 2n
a
−
1
a
0
a
p
1
p
1
p
1
p
1
)0(z)0(pz
)0(zp
2n−
)0(zp
1n−
n
b
1n
b
−
2n
b
−
1
b
0
b
)
p
(
z
y
(-)
б)
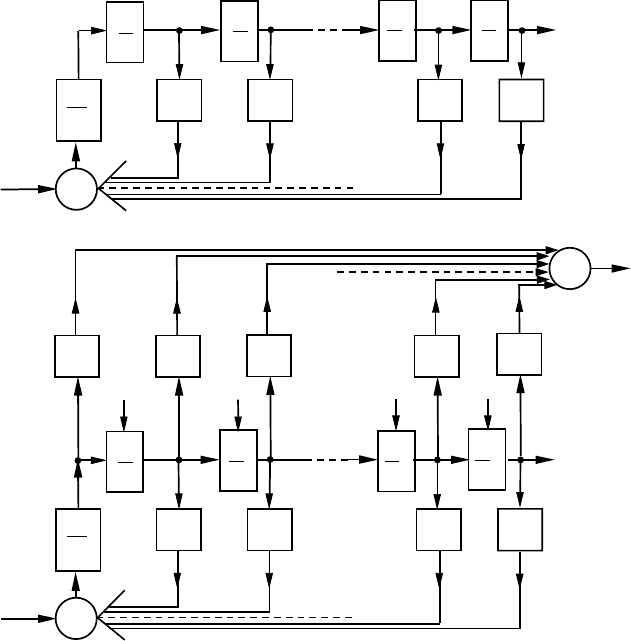
Рис.1.7. Структурні моделі перетворення входу в стан (а) та
вихід (б) для системи загального виду.
Ці формули можна отримати, записавши за структурною
моделлю рис.1.8 передатну функцію і прирівнявши коефіцієнти
її чисельника коефіцієнту
для відповідних степеней
k
b
p
у
передатній функції (1.9).
31
n
z
1
z
1n
a
− 0
a
p
1
p
1
p
1
)0(z
1
)0(z
n
n
β
1n−
β
0
β
n
a
1
)0(z
1n−
1n
z
−
2n
a
−
:)t(y
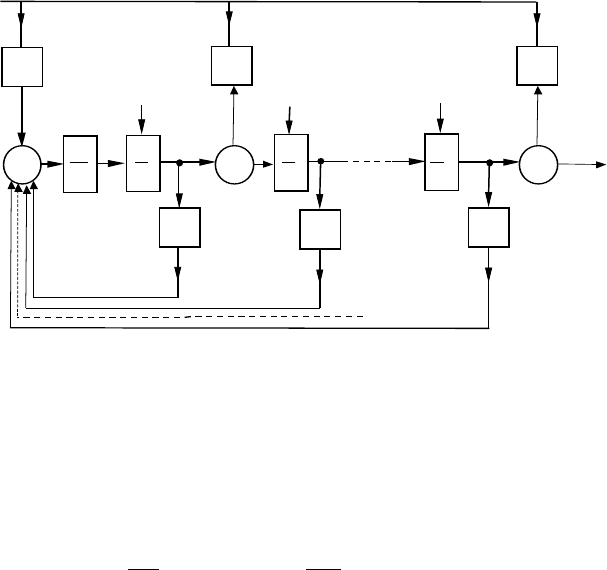
Рис 1.8. Варіант структурної моделі для системи загального виду
За структурною моделлю рис.1.8 легко записати систему n
рівнянь першого порядку
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+−=
+=
+=
∑
=
t
)
(
u
a
)
t
(
z
a
a
1
)
t
(
z
................................
)
;t(u
)
t(
z
)
t(
z
)
;
t
(
u
)
t
(
z
)
t
(
z
n
n
i
n
0i
i
n
n
232
121
β
β
β
(1.35)
і представити її в розгорнутій матричній формі
)
,t(u
)t(z
)t(z
)t(z
)t(z
1000
0100
0010
)t(z
)t(z
)t(z
)t(z
n
1n
2
1
n
1n
2
1
1n210n
1n
2
1
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
+
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−−−−
=
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−−
−
−
β
β
β
β
αααα
…
…
…
(1.36)
32

де
n
i
i
a
a
=
α
і записати векторне рівняння:
)t(uB)t(zA)t(z
+
= (1.37
Рівняння (1.36) і (1.37) відрізняються від (1.8) і (1.9) тільки
вектором
B
. Структурна модель на рис. .8 ілюструє, що в
цьому випадку вектор стану системи
1
)
t
(
z
є сукупність
сигналів на виходах інтеграторів (рис.1.4,г), яких вхідні сигнали
формуються як лінійні комбінації змінних стану
. і
керувань, що розподіляються вектором вхідних коефіцієнтів
)t(z
i
B
(блок В і суматор на рис.1.4,г) . Скалярний вихід у(t) формується
з компонента
і керування u(t) як )t(z
1
)t(u)t(y
0
β
=
.
Передатну функцію загального виду (1.30) також можна
розкласти на елементарні співмножники, знайшовши не тільки її
полюси (1.12) , але і нулі як корені рівняння
,0bpbpbpb
01
1m
1m
m
m
=++++
−
−
… (1.38)
яке отримують, прирівнявши до нуля чисельник передатної
функції.
Передатну функцію у вигляді добутку елементарних
співмножників
()
()
()
,
p
p
pW
n
0i
i
m
0k
k
∏
∏
=
=
λ−
ν−
=
(1.39)
де
i
λ
- полюси і
k
ν
- нулі передатної функції, розглядають як
послідовне з'єднання типових ланок виду:
,
p
p
)p(W
l
l
1
λ
ν
−
−
= (1.40)
33

- інерційно-диференіцюючої ланки;
,
p2p
p
)p(W
2
r0r0r
2
r
2
ωωξ
ν
++
−
= (1.41)
- коливальної ланки з диференціюванням;
,
p2p
p2p
)p(W
2
q0q0q
2
2
s0s0s
2
2
ωωξ
ωωξ
++
++
=
(1.42)
- коливальної ланки з подвійним диференціюванням. Їхні
структурні моделі утворюються як окремі випадки загальних
моделей рис.1.7,б і рис.1.8 при
n
=
1 та n
=
2 .
Якщо власні значення
n2,1
...
λ
λ
λ
матриці A системи - дійсні
різні числа, то, використовуючи перетворення
),t(zP)t(x
1
−
= (1.43)
де
P
- матриця Вандермонда, систему (1.37) можна привести до
виду:
),t(uBP)t(x)t(x
1
−
+=
Λ
(1.44)
де
Λ
- діагональна матриця власних значень. Перетворення
зміню вектор керування є
.b
P
V
11 −−
=
(1.45)
Використовуючи останнє співвідношення, можна записати:
),t(uV)t(x)t(x
+
=
Λ
(1.46)
Система (1.46) відрізняється від (1.27) тільки вектором
керування, компоненти якого як і раніше дорівнюють різницям
передаточної функції системи в полюсах і можуть бути
розраховані методом невизначених коефіцієнтів. Структура
математичної моделі для рівнянь (1.45) і (1.46), показана на
рис.1.7, відрізняється від структури на рис.1.9 додатковим
блоком прямої передачі
, причому
0
V 0V
0
≠
тільки при mn
=
,
при
mn< 0V
0
=
і структури однакові.
34
ν
n
x
n
(
)
yt
()
ut
x
1
x
i
ν
1
1
p
λ
1
1
p
λ
n
ν
0
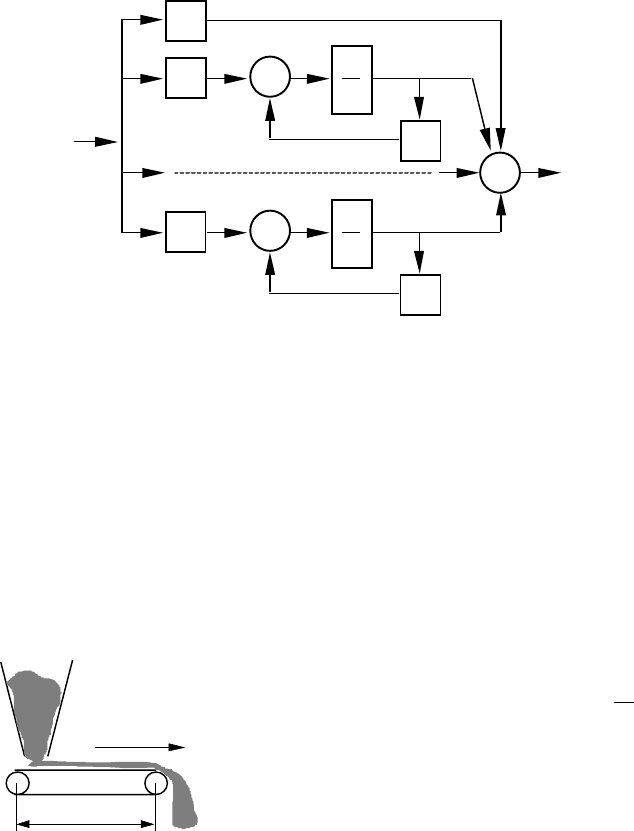
Рис.1.9. Паралельна структура для системи загального виду
Різні варіанти структурних представлень динамічних
процесів зручні для оцінки практичного змісту і реальної
цінності різних теоретичних пропозицій для аналізу
електромеханічних систем і керуванню реальними об'єктами.
1.9. Моделювання елементів чистого запізнювання
Елементи чистого запізнювання - динамічні ланки, у яких
вихідний сигнал у точності відтворює вхідний, але затримує
його появу на деякий час
τ
. Прикладом може послужити
конвеєрна установка (рис.10.1).
При транспортуванні порода, що
зсипається в точку 1, через час
τ=
L
V
переміщається в точку 2.
Передатна функція такої ланки:
(
)
Wp e
p
=
−τ
. (1.47)
Рівняння ланки в часовій області:
(
)
(
)
gt f t
=
−
τ , (1.48)
де
- інтервал запізнювання, с. τ
1 2
V
L
Рис.1.10. Конвеєрна
установка
35
