Чорний О.П., Луговой А.В. и др. Моделювання електромеханічних систем
Подождите немного. Документ загружается.


де
.
()()()()()
[]
∫
−−−−−−=
−−
N
t
0
1m
N
1m2
NN
dt!1m/tt1,...,tt5.0,tt,1
T
H
Одержуємо попередне узагальнене рішення
.
Аналогічно вирішуються інші задачі: прогноз із
диференціюванням, інтерполяція з диференціюванням, прогноз з
інтегруванням і інші.
()
hHAV
T
=
3.3. Моделювання сил тертя ковзання і кочення
Всі опори механізмів спираються на підшипники кочення
(кулькові, роликові) і ковзання (сталь по сталі, сталь по латуні та
ін.).
Для підшипників ковзання залежність моменту опору
можна записати в загальному вигляді:
M
cm
MMMMM
cm з Q
=
+
+
+
р µν
, (3.7)
де
- момент зрушення; - момент, зумовлений
в'язкістю мастила;
- момент, зумовлений тертям об повітря;
- статичним навантаженням на підшипник.
M
зр
M
ν
M
Q
M
µ
M
зр
- зумовлений нерівномірністю розподілу мастила
після зупинки. Мастило стікає в нижню частину і гусне або
застигає при низьких температурах.
()
Mm
зр
=+
−
εν ϕ
2
3
1
1 , (3.8)
де
- коефіцієнт, що залежить від конструкції підшипника і
його типорозмірів;
ε
ν
- кінематична в'язкість мастила (сСт);
ϕ
-
кількість обертів із моменту початку обертання;
- кількість
підшипників.
m
Вигляд залежності моменту зрушення
від кількості
обертів
ϕ наведено на рис.3.12.
M
зр
85
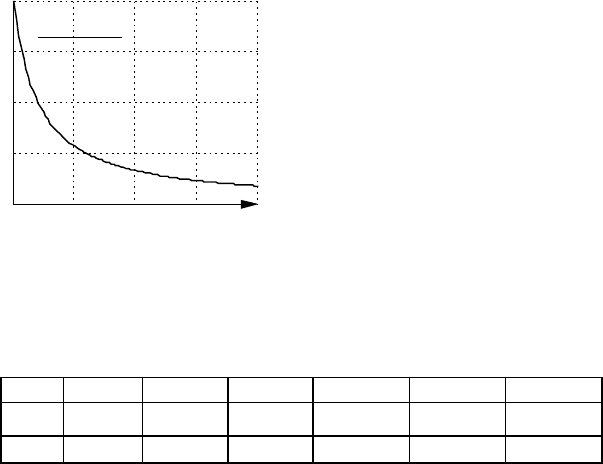
Орієнтовні значення
коефіцієнта
ε
, визначені
емпірично для
перетворювальних агрегатів Г-
Д деяких кар'єрних
екскаваторів, наведені в
таблиці 3.5.
0 2.5 5 7.5
0
0.25
0.5
0.75
1
M
M
з
з
р
р.max
ϕ
Рис.3.12. Залежність моменту
зрушення від обертів ротора
Таблиця 3.5.
Значення коефіцієнта
ε
залежно від потужності привідного СД
агрегата Г-Д
Тип ЕКГ-8І ЕКГ-12.5 ЕКГ-15 ЕШ 10.70 ЕШ 10.70 ЕШ 10.70
P
нсд.
630 1000 1250 1250 1900 2500
ε
15.98 33.03 36.83 45.56 50.06 80.96
Залежність моменту опору від в'язкості мастила може бути
виражена формулою Стокса :
M
ν
r
π
ν
ω
= 6 , (3.9)
де
r
- радіус кульки в підшипнику (м);
ω
- кутова швидкість
(рад/с).
Величина статичної в'язкості мастила є складною функцією,
що залежить від температури і швидкості обертання.
Апроксимацією характеристик мастил отримана усереднена
залежність їх в'язкості від температури навколишнього
середовища
t
C
D
.
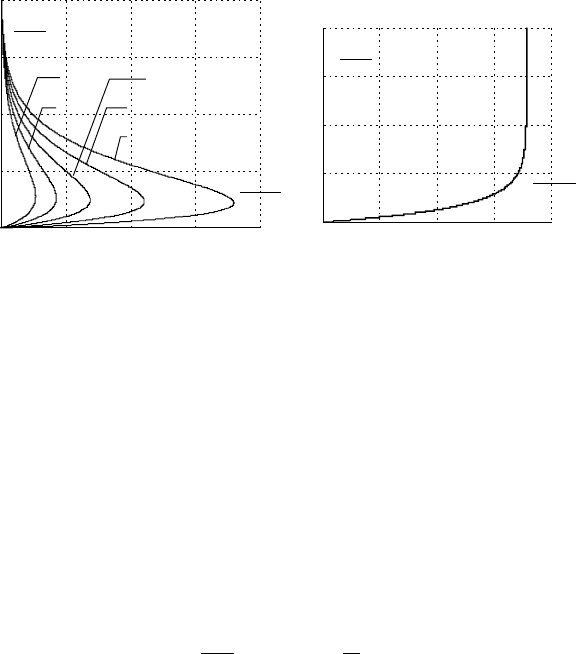
З урахуванням отриманого рівняння графічна
залежність моменту від в'язкості мастила при різних
температурах має вигляд наведений на рис.3.13.
()
(
)
(
)
lg ναωβ αωβ=−+−+
11 2
t
D
2
, (3.10)
де
α ;
1
5
66 10=⋅
−
.
α
2
0 0111
=
. ;
β
1
0 02334= . ;
β
2
3 24165
=
. .
86
0 0.07 0.15 0.23 0.3
0
0.25
0.5
0.75
1
ω
ω
н
M
M
н
ν
20
D
10
D
0
D
−10
D
−20
D
0 0.01 0.02 0.03 0.04
0
0.25
0.5
0.75
1
ω
ω
н
M
M
н
µ
Рис.3.13. Залежність моменту Рис.3.14. Залежність
моменту опору від в'язкості статичного навантаження
мастила від швидкості
Момент, що залежить від статичного навантаження на
підшипник, може бути представлений виразом, що враховує як
вагу ротора, так і швидкість обертання:
(
)
MgGre
µ
ξω
µ=−
−
0
1 , (3.11)
де
- приведений коефіцієнт тертя (µ
0
µ
0
0 001 0 0015
=
÷
..для
тертя типу сталь по сталі);
G
- вага ротора, кг;
r
- радіус вала,
м;
g
= 981. м/сP
2
P
;
ξ
=
004. - емпіричний коефіцієнт. Залежність
моменту статичного навантаження наведена на рис.3.14.
Момент тертя ротора електричного двигуна об повітря:
M
l
d
Q
н
=⋅
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
−
4 665 10 1 4 4
3
17
44
.
.
.
ω
ω
., (3.12)
де
- довжина ротора, м; d - діаметр ротора, м. l
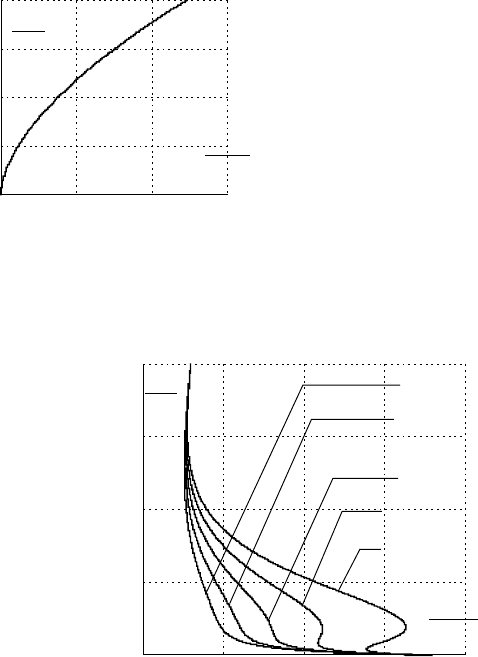
Залежність моменту тертя об повітря має вигляд наведений
на рис.3.15.
Сумарна залежність (3.7)
(
)
Mf
cm
=
ω
наведена на рис.
3.16.
87
Для підшипників ковзання
наведена залежність
(
)
Mf
cm
=
ω
теж правильна. Дещо
відрізняються принципи
формування моментів. Для малих
швидкостей має місце тертя вала
об підшипник, але при зростанні
швидкості тертя зменшується,
оскільки поверхні ковзання
віддалені одна від одної (між ними
утвориться тонкий шар мастила),
при зростанні
ω
товщина цього шару збільшується і вал ніби то
спливає на мастилі (так званий гідродинамічний підйом вала) і
момент опору різко зменшується.
0 0.01 0.02 0.03
0
0.25
0.5
0.75
1
ω
ω
н
M
M
Q
н
Рис.3.15. Залежність моменту
тертя об повітря.
0 0.1 0.2 0.3 0.4
0
0.25
0.5
0.75
1
ω
ω
н
M
M
cm
н
20
D
10
D
0
D
−10
D
−20
D
Рис. 3.16. Сумарна залежність статичного моменту
При подальшому зростанні
ω
, починає діяти сила тертя об
мастило і момент опору збільшується. Приблизний вигляд
переміщення вала наведено на рис.3.17.
88
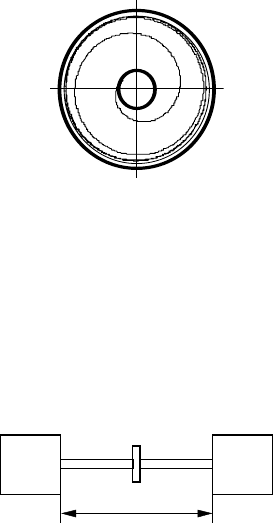
Рис 3.17. Переміщення вала в підшипнику ковзання при
зростанні швидкості.
3.4. Моделювання механічної частини електропривода з
урахуванням пружності
У перехідних (динамічних) режимах, усі елементи
механічних ланок, до яких прикладається момент, піддаються
деформаціям. Розглянемо процес передачі моменту від двигуна
до робочої машини:
РМ
Д
l
Рис.3.18. З'єднання двигуна і робочої машини.
Між двигуном (Д) і робочою машиною (РМ) завжди є
ділянка вала довжиною
(рис.3.18). Уявимо, що двигун і
робоча машина з'єднані гумовим валом. Коли починає
обертатися двигун, то спочатку відбувається скручування вала.
Кінець вала з боку двигуна обертається, а кінець вала з боку
робочої машини ще нерухомий. Відбувається деформація вала.
l
Відповідно до закону Гука, виникаючі пружні моменти
пропорційні кутовим деформаціям:
Mc
np
=
⋅
∆
ϕ ,
де
c - коефіцієнт пружності.
Розрахунок пружностей механічних з’єднань при
моделюванні викликає найбільші труднощі. Розрахунок деяких
коефіцієнтів
с можна виконати за наступними виразами.
89

Для сталевих валів
с G
d
l
=
π
32
4
,
де
G =
⋅
8
7
10
5
. кг/смP
2
P
; G
=
⋅853 10
10
. Н/мP
2
P
; - діаметр і
довжина вала, см.
dl,
Для сталевих канатів (лінійна деформація) під час
багаторазового підйому
c
m
Hm
kk
=
⋅
−
−
111 10
160 10
8
42
.
H
,
де
H
k
- довжина каната, м; - запас пружності каната. m
Із збільшенням значення коефіцієнта пружності
механічна частина стає більш жорсткою і деформація
зменшується.
c
При
c →
∞
рух, переданий від Д до РМ, не перекручується
і механічну частину привода можна розглядати як одномасову
систему (рис.3.19):
ω
M
cm
M
дв
J
Σ
Рис.3.19. Еквівалентна одномасова система.
Момент інерції робочої машини приводиться до вала
двигуна. Швидкості двигуна і робочої машини збігаються. У
деяких випадках коефіцієнт жорсткості
виявляється
невеликим і деформація стає суттєвою. Наприклад: конвеєри,
шахтні підйомні установки (ШПУ). Таких мас, з'єднаних валами,
може бути декілька. Аналіз багатомасових систем надзвичайно
складний, тому всі махові маси зазвичай зводять до двох:
двигуна з моментом інерції
і робочої машини відділеної
пружним моментом
і моментом інерції .
c
J
1
M
np
J
2
Така механічна структура являє собою двомасову систему
(рис.3.20).
90
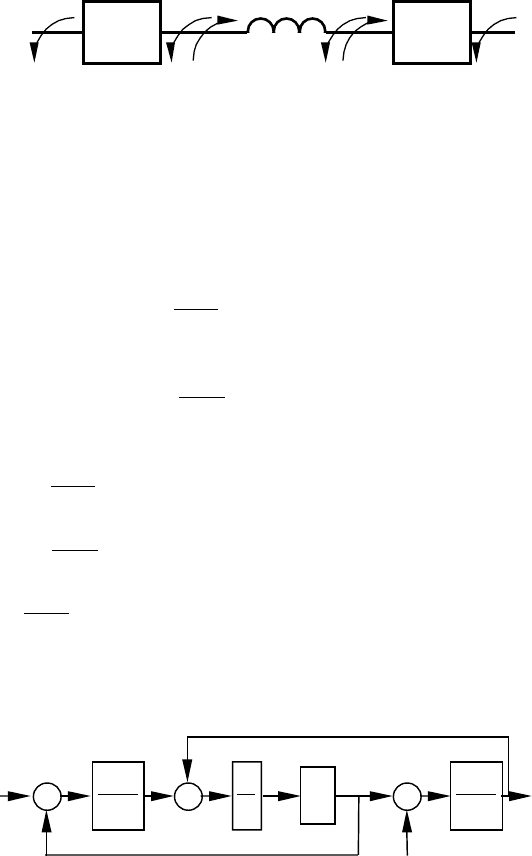
c
12
ω
1
M
np
M
np
M
cm
M
дв
J
1
J
2
ω
2
Рис.3.20. Еквівалентна двомасова система з пружним зв’язком
Кутова деформація пружного елемента може бути
виражена:
(
∆ϕ = −
∫
ωω
12
0
dt
t
)
. (3.13)
Рівняння руху 1-ї маси
MM J
дв np
−=
1
1
d
dt
ω
. (3.14)
Рівняння руху 2-ї маси
MM J
np cm
−=
2
2
d
dt
ω
. (3.15)
Остаточно система диференційних рівнянь двомасової системи:
JMM
JMM
Mc
дв np
np cm
np
1
1
2
2
12
12
d
dt
d
dt
d
dt
ω
ω
ωω
=−
=−
=−
=⋅
⎧
⎨
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
;
;
;
.
∆ϕ
∆ϕ
(3.16)
Структурна схема двомасової системи складеної за
рівняннями (3.16) наведена на рис.3.21.
1
p
ω
1
∆
ϕ
()
−
()
−
()
−
ω
1
M
cm
M
np
M
дв
1
1
Jp
c
12
1
1
Jp
Рис.3.21. Структурна схема двомасової системи
91
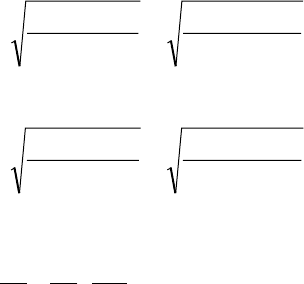
Таким чином, двомасова механічна система подається
структурною схемою з перехресними зворотними зв'язками,
тобто має підвищену схильність до виникнення коливальних
режимів. Дана система отримана за умови, що моментом
внутрішнього тертя на валу можна знехтувати, оскільки
істотнішим виявляється момент зовнішнього опору, викликаного
навантаженням.
Дуже важливим при моделюванні динаміки руху двомасової
системи є
вибір кроку інтегрування, оскільки від цього залежить
обсяг обчислень і точність отримуваного результату.
Орієнтиром у цьому питанні можуть бути динамічні властивості
системи, що визначаються резонансними частотами:
(
)
(
)
21
2112
21
2112
12
mm
mmc
JJ
JJc
⋅
+
′
=
⋅
+
=Ω
.
Для тримасової механічної системи визначається також
частота вільних коливань при взаємодії другої та третьої мас:
(
)
(
)
32
3223
32
3223
23
mm
mmc
JJ
JJc
⋅
+
′
=
⋅
+
=Ω
.
Для кожного коливання потрібно розрахувати не менше як
25-30 точок, тобто крок інтегрування приймається таким:
m
2
30
1
25
1
h
Ω
π
⎟
⎠
⎞
⎜
⎝
⎛
÷=
,
де
Ω - більша з частот.
m
3.5. Моделювання зазору в механічній передачі
Передаточні механізми, що з’єднують двигун та робочу
машину не завжди являють собою суцільні вали, планетарні
передачі або канати. В більшості випадків між двигуном та
робочою машиною встановлюють редуктори для зміни
швидкості обертання. Механічне з’єднання за допомогою
шестерень потребує урахування впливу зазору на динаміку
двомасової механічної системи. Розглянемо рівняння двомасової
системи за цієї умови.
92
Наявність зазору робить залежність
(
)
Mf
np
=ϕ
нелінійною. Для урахування цієї нелінійності розглянемо вплив
зазору на прикладі зубчастої передачі (рис.3.22.).
На початку руху ротора двигуна робоча машина
залишається нерухомою через зазор. Пружний момент при
цьому
M
np
=
0 . Після вибирання зазору робоча машина
починає обертатися. З'являється пружний момент.
Залежність
(
)
Mf
np
=ϕ має вид нелінійності типу
"нечуттєвість", графік якої показаний на рис.3.23.
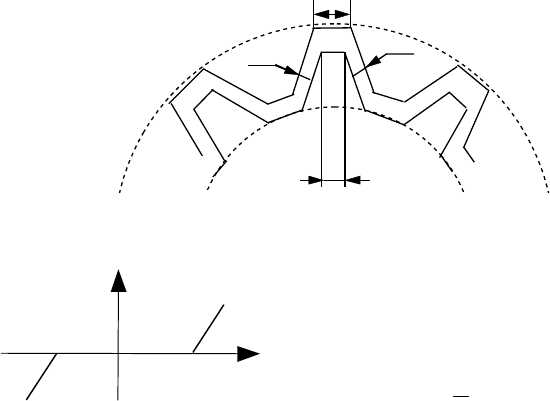
δ
2
δ
1
l
1
l
1
Рис. 3.22. До визначення зазору в механічній передачі.
Величина зазору
δ
1
і
δ
2
залежить від початкового
положення передачі. Зазвичай
беруть
2
21
δ
=δ=δ , (3.17)
де
δ
=
−
ll
12
Система диференційних
рівнянь двомасової механічної системи з урахуванням зазору
має вигляд (3.18). Структурна схема, що відповідає даній
системі рівнянь наведена на рис.3.24.
∆
ϕ
δ
2
δ
1
M
np
Рис.3.23. Нелінійна
залежність пружного моменту
за наявності зазору
93
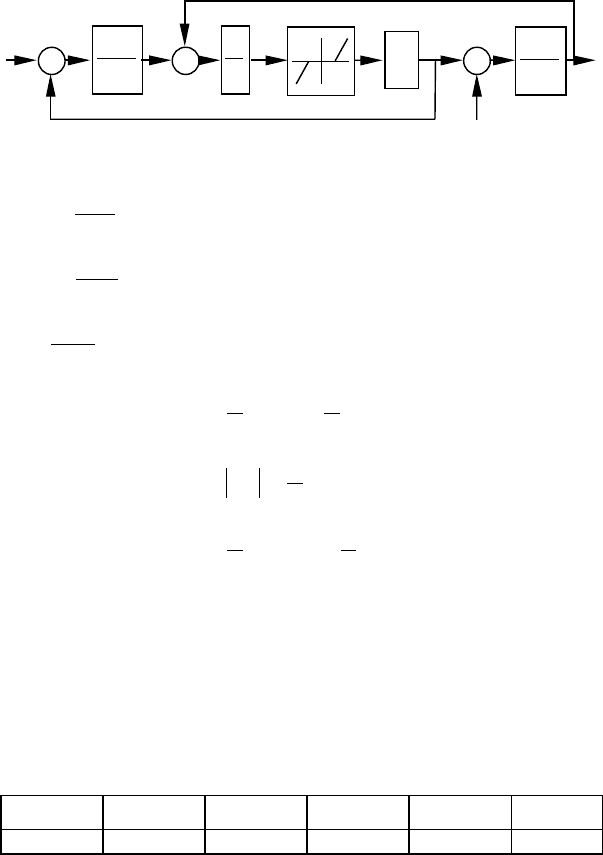
M
np
()
−
1
p
ω
1
∆
ϕ
()
−
()
−
ω
1
M
cm
M
д
в
1
1
Jp
c
12
1
1
Jp
Рис.3.24. Структурна схема двомасової системи з урахуванням
зазору
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎧
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
δ
−≤ϕ∆
⎟
⎠
⎞
⎜
⎝
⎛
δ
+ϕ∆
δ
<ϕ∆
δ
≥ϕ∆
⎟
⎠
⎞
⎜
⎝
⎛
δ
−ϕ∆
=
ω−ω=
ϕ∆
−=
ω
−=
ω
.
2
,
2
c
;
2
,0
;
2
,
2
c
np
M
;
dt
d
;MM
dt
d
J
;
MM
dt
d
J
12
12
21
cmnp
2
2
npЉ‰
1
1
(3.18)
Приклад.
Розрахуємо динаміку двомасової системи при пуску з постійним
рушійним моментом. Вихідні дані для розрахунку наведені в таблиці
3.6.
Таблиця 3.6.
Вихідні дані для розрахунку динаміки двомасової системи з
пружностями.
M
дв
,Нм M
cm
,Нм J
1
,кгмP
2
P
J
2
,кгмP
2
P
c
12
2
δ
, сP
-1
P
100 50 0.1 0.4 5000 0.1
Для моделювання використаємо модель зображену на рис.3.24.
Крок інтегрування складає 0.001 с.
Структурна схема моделі при використанні розширення пакета
94
