Чорний О.П., Луговой А.В. и др. Моделювання електромеханічних систем
Подождите немного. Документ загружается.

Динамічні процеси, відповідно до розрахункової схеми,
описуються такими системами рівнянь:
∂
∂
∂υ
∂
∂υ
∂
∂
∂
F
x
m
t
xES
F
t
k
k
+=
+=
⎧
⎨
⎪
⎪
⎩
⎪
⎪
1
0
1
0
;
.
, (10.1)
() ()
()
m
d
dt
Ft Ft
m
d
dt
Ft
н
дв н
k
k
1
2
υ
υ
=−
=
⎧
⎨
⎪
⎪
⎩
⎪
⎪
;
.
, (10.2)
де
- зусилля в перерізі каната; - швидкість переміщення
розрізу каната;
F υ
S
k
- площа поперечного розрізу каната;
E
-
модуль пружності каната;
m
k
1
- маса одиниці довжини каната;
FF
н
k
, - зусилля, відповідно, у нижньому і верхньому розрізах
каната;
- рушійне зусилля, що створює електропривод;
- зосереджені ведуча і ведена маси;
F
дв
mm
1
,
2
υ
б
k
k
ES
m
=
1
-
швидкість поширення хвилі пружної деформації.
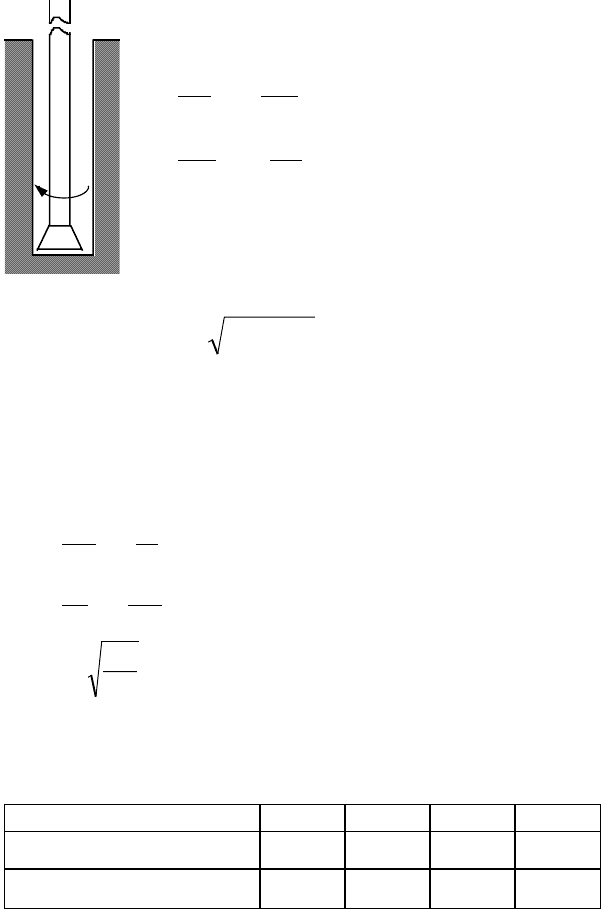
10.2. Механічна частина електропривода бурової
установки
Розглянемо роботу електропривода обертання бурового
верстата. Робочий орган - бурова коронка - обертається за
допомогою колони з бурових труб (рис.10.2).
Бурова колона при великій довжині також є пружним
робочим органом із розподіленими по довжині пружністю і
внутрішнім тертям.
232
Колона бурових труб, у вигляді
однорідного стрижня, описується системою
диференційних рівнянь у частковних похідних:
∂ω
∂
∂
∂
∂
∂
∂ω
∂
x
k
M
t
M
x
J
t
у
m
+=
+=
⎧
⎨
⎪
⎪
⎩
⎪
⎪
0
0
, (10.3)
де
ω
- кутова швидкість обертання бурової
колони;
M
- момент кручення в розрізі; -
коефіцієнт пружності;
- момент інерції
одиниці довжини бурової колони;
k
y
J
m
my
Jk/1=
υ
- швидкість поширення хвилі
пружних коливань уздовж бурової колони.
Рис.10.2.
Бурова колона
Слід відзначити повну ідентичність рівнянь коливань у
канатах підйомної установки і коливань у буровій колоні.
За формою ці рівняння збігаються з добре відомими
рівняннями поширення електромагнітних хвиль уздовж лінії
електропередачі, що мають вид:
∂
∂
∂
∂
∂
∂
∂
∂
U
x
L
i
t
i
x
C
U
t
+=
+=
⎧
⎨
⎪
⎪
⎩
⎪
⎪
0
0
, (10.4)
υ=
1
LC
. (10.5)
Узагальнюючи ці три системи, приходимо до наступної
електромеханічної аналогії (табл 10.1).
Таблиця 10.1.
Електромеханічні аналоги електромеханічних систем
Лінія електропередачі
U
I
L
C
Канат
F
υ
m
k
1
k
ES/1
Буровий верстат
M
ω
J
m
k
y
233
Диференціюючи перше рівняння в системі за , а друге
рівняння - за
t
x
, за виключенням функції
U
, одержимо:
∂
∂∂
∂
∂
∂
∂
∂
∂∂
22
2
2
2
2
0
0
U
xt
L
i
t
i
x
C
U
xt
+=
+=
⎧
⎨
⎪
⎪
⎩
⎪
⎪
; (10.6)
2
2
2
2
x
i
LC
1
t
i
∂
∂
+
∂
∂
(10.7)
Аналогічно для напруг:
∂
∂
∂
∂
2
2
2
2
1U
t
LC
U
x
= . (10.8)
Таким чином, вирішення рівняння руху для розглянутих
вище систем зводиться, в остаточному вигляді, до рішення
хвильових рівнянь, що відносяться до класу гіперболічних
рівнянь у часткових похідних.
У системі хвильових рівнянь не враховуються розподілені
за довжиною втрати, що спрощують і знижують точність моделі.
Для одержання вирішення рівнянь у часткових похідних
необхідно
задати початкові і граничні умови. Для розглянутої
моделі:
граничні умови -
(
)
(
)
it iilt i
k
0
0
,,,==
;B
початкові умови -
(
)
(
)
ix f x,0 =
,
де
- функція від просторової координати
()
fx
x
.
У багатьох випадках пошук і коректне задання початкових і
граничних умов є окремим, дуже складним завданням.
10.3. Математичне моделювання електроприводів
турбомеханізмів
До турбомеханізмів відносяться такі класи об’єктів: насоси,
вентилятори, компресори та ін. Це механізми, призначені для
транспортування рідин і газів.
234

Робота турбомеханізмів тісно
пов'язана з комунікаційними
мережами: вентиляційними
каналами шахт; напірними
трубопроводами насосів і т.п.
Розглянемо, наприклад, систему
провітрювання шахти (рис.10.3).
головний
ствол
ГВУ
l
м
=÷50 100
вентиля-
ційний
канал
Рис.10.3. Схема вентиляції
шахти
Статичний момент
електропривода турбомеханізма
визначається за формулою:
M
HQ
=ρ
ω
00
, (10.9)
де
- тиск і продуктивність вентиляторной установки в
нульовому перетині.
HQ
0
,
0
Оскільки
; H
0
2
~ ω Q
0
~
ω
, то в усталеному режимі:
. M~ω
2
Однак у реальних умовах
і залежать не тільки від
кутової швидкості електропривода, але і від режиму роботи
комунікаційної мережі (КМ), на яку працює турбомеханізм.
Комунікаційна мережа, у свою чергу, є складним динамічним
об'єктом.
H
0
Q
0
Рівняння, що описують динамічні процеси в загальному
вигляді, представлені рівняннями руху механічної частини
()
(
)
;
dt
d
JMM
2
c
ω
ωω
Σ
=−
()
(
)
;M
0
ω
ω
β
ω
−
=
()
(
)
(
)
;
,0Q,0H
M
2
2
c
ρ
ω
ωω
ω
=
(10.10)
()
(
)
()
;,0Q
Q
H0H
QH
’
cm
ω
−
=∆
()
()
.QHH,0H
2
’
cm
2
∆−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
ω
ω
ω
235
і рівняннями поширення хвиль тиску і продуктивності в рідких і
газоподібних середовищах (рівняння Нав'є-Стокса)
−= +
⎛
⎝
⎜
⎞
⎠
⎟
−= ⋅
⎧
⎨
⎪
⎪
⎩
⎪
⎪
∂
∂
ρ∂
∂
∂
∂
ρ
∂
∂
H
xS
Q
t
aQ
H
t
c
S
Q
x
2
2
, (10.11)
де
- момент двигуна і момент опору; MM
c
,
ω
ω
0
, - кутова
швидкість турбомеханізму в точці статичної рівноваги і поточна
кутова швидкість;
- повний напір, що розвивається
турбомеханізмом і статичний напір;
HH
cm
,
β
- жорсткість механічної
характеристики двигуна;
- поточна і номінальна
продуктивності механізму;
QQ
н
,
(
)
H0 - напір, що розвивається при
закритій заслінці;
∆
H
- утрати напору у проточній частині
турбомеханізма,
H
Q, - тиск і утрати в деякій частині перерізу
трубопроводу;
ρ
- густина рідини або газу;
S
- площа
поперечного перерізу;
- швидкість звуку в середовищі; -
середнє значення коефіцієнта розподілених утрат тиску на
внутрішнє тертя.
c a
Ці рівняння відрізняються від отриманих вище рівнянь
електромеханічної аналогії наявністю додаткового складового в
першому рівнянні, що враховує розподілені втрати.
Рівняння трубопроводу за формою збігаються з рівняннями
довгої лінії при наявності в ній втрат.
Для чисельного рішення таких систем рівнянь
використовується метод
сіток або метод кінцевих елементів.
Розглянемо один з різновидів методу кінцевих елементів.
Представимо частину КМ уздовж просторової координати
x
,
розділену на деяке число інтервалів рівної довжини
N
(рис.10.4). На кожному інтервалі тиск і продуктивність будуть
сталими.
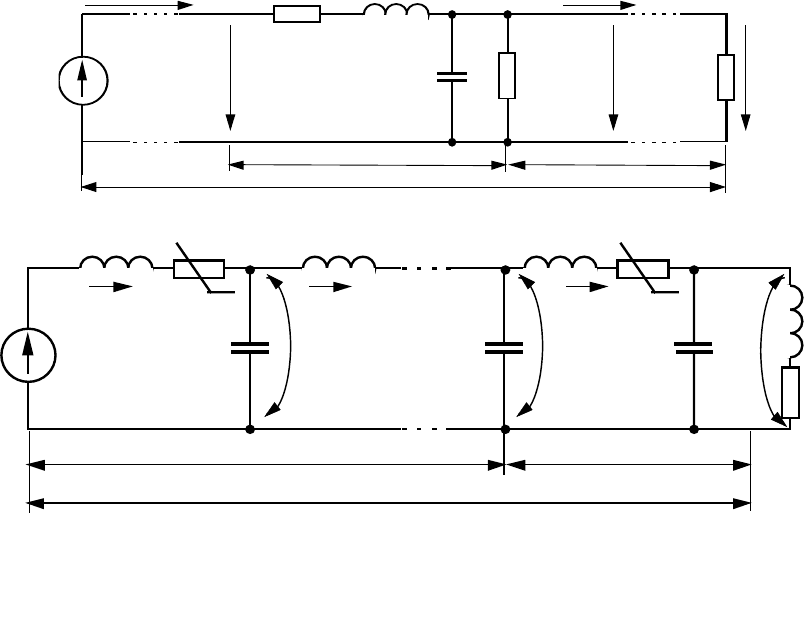
236
U
н
l
x
dx
()
,Ux dxt+
Z
(
)
,Uxt
Gdx
0
Cdx
0
E
0
(
)
ixt,
()
ix dxt+ ,
Ldx
0
Rdx
0
Рис. 10.4. Зображення трубопроводу довгою лінією при наявності в ній втрат
C
0
H
n
H
1
H
0
Q
1
Q
0
R
0
R
0
L
0
L
0
R
н
L
н
L
0
Q
n
−
1
C
0
l
x
′
x
C
0
H
n−1
Рис.10.5. Зображення трубопроводу з’єднанням чотириполюсників
237

Таке перетворення відповідає заміні довгої лінії
ланцюговим з'єднанням
N
чотириполюсників (рис.10.5.),
де
R
c
S
L
c
S
c
S
c
000
2
2
===ρ
λ
ρ
ρ
;;
- питомі акустичні параметри
КМ,
x
- коефіцієнт утрат напору.
Тоді для i-го чотириполюсника рівняння тиску і
продуктивності будуть мати вигляд:
dQ
dt
HH RQ
L
dH
dt
QQ
c
iii i
ii i
=
−
−
=
−
⎧
⎨
⎪
⎪
⎩
⎪
⎪
−
−
10
0
1
0
;
.
. (10.12)
Таким чином, система рівнянь турбомеханізму, що реально
складається з двох диференційних рівнянь у часткових похідних,
наближено заміняється системою з
24
N
+
звичайних
диференційних рівнянь.
Зі збільшенням
N
зростає точність одержуваних рішень,
однак при цьому швидко збільшується обсяг обчислень, тому в
інженерній практиці звичайно беруть
N
=
÷
810.
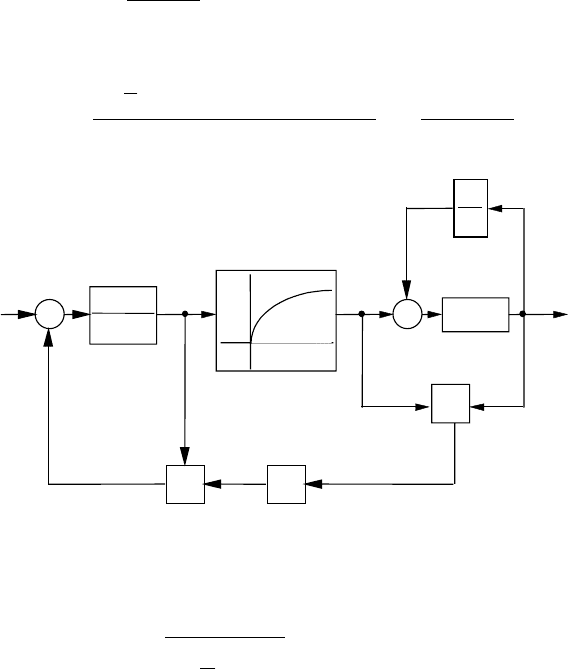
Структурна схема системи електропривода турбомеханізму
і комунікаційної мережі у вигляді довгого трубопроводу
подається на рис.10.6.
Передатна функція прямого каналу системи двигун-
турбомеханізм-КМ має вигляд:
()
(
)
(
)
(
)
WpWpWpW p
пк дв нл тм км
=⋅⋅
−
, (10.13)
де
- передатна функція електромеханічної системи:
()
Wp
дв
Wp
Tp
дв
м
()=
+
1
1
, (10.14)
TJ
M
м
c
=
Σ
ω
0
;
()
Wp
нл
- передатна функція нелінійної ланки турбомеханізму:
238
Wp
Hp
p
нл
()
()
()
=
∆
∆ω
; (10.15)
передатна функція комунікаційної мережі:
()
()()
()()
Wp
ee ee
ee ee
th p
th p
км
pppp
pppp
=
−− +
−+−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
−
−−
−
−−
3
1
1
2
1
3
2
2
1
ττττ
ττττ
τ
τ
()
()
. (10.16)
()
∆
h
p
() ()
∆∆
H
p
Q
p
⋅
()
∆
Q
p
()
∆
H
p
()
∆ω
p
()
−
()
−
()
∆
M
p
c
ρ
g
()
∆
P
p
()
∆
M
p
1
1T
p
м
+
∆
H
∆ω
ω
0
H
0
×
c
Sg
()
W
p
kc
÷
Рис.10.6. Структурна схема системи електропривода
турбомеханізму і комунікаційної мережі
Передатна функція системи турбомеханізм-КМ
()
Wp
th p
th p
тм кс−
=
−
()
()
τ
τ3
1
2
. (10.17)
Приклад.
На прикладі електропривода шахтної вентиляційної установки
виконаємо розрахунки перехідних процесів у розімкненій системі.
Параметри вентилятора та комунікаційної мережі наведені в табл
10.4
Таблиця 10.2.
239

Номінальні та вихідні дані вентиляторної установки та шахтної
комунікаційної мережі
Параметр Значення
Номінальна потужність двигуна, , кВт Р
н
100
Синхронна швидкість обертання , об/хв n
0
1500
Діаметр воздуховоду, , м d
1
Переріз повітропроводу,
S
, мP
2
P
0,785
Довжина повітропроводу, , м L
150
Номінальний видаток, , мP
3
P
/с Q
н
50
Номінальний натиск, , м H
н
158
Номінальний опір мережі, , Мом R
н
0,2
Індуктивність мережі, , Гн L
н
0,5
Момент інерції електроприводу, , кг мP
2
P
J
Σ
160
Електромеханічна стала часу, T , с
м
0
1,5
Швидкість звуку, , м/с с 334
Густина середовища,
ρ
, кг/мP
3
P
1,17-1,29
Коефіцієнт теплопровідності,
λ
0,000015
Розрахунки перехідних процесів виконаємо для систем
диференційних рівнянь при 20 чотириполюсниках:
()
dQ
dx
HHRQL
1
12010
1
=−−
−
;
dH
dt
1
0= ;
Для
2 ≤
≤
i
N
()
dQ
dx
HH RQL
i
ii i
=− −
+
−
10 0
1
;
()
dH
dt
QQC
ii
1
10
1
=−
−
−
;
................
()
dQ
dx
HRQL
н
нннн
=−
−1
;
240
()
dH
dt
QQC
н
N н
=−
−
0
1
та рівнянь руху електромеханічної системи:
()
T
d
dt
M
м
c
0
0
ω
ωω
β
=−−
;
MH Q
c нн
=
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
1
00
2
0
ω
ω
ω
ω
ω
.
Результати спільного рішення систем з використанням методу
Рунге-Кутта наведені на рис.10.7.-10.8.
При обмеженій кількості інтервалів розбиття трубопроводу на
графіку видатку з’являються високочастотні коливання Гіббса. Для їх
згладжування необхідно збільшувати кількість ділянок розбиття
трубопроводу, що приводить до підвищення порядку системи та до
значного збільшення часу розрахунку моделі.
На рис.10.10.
зображені перехідні процеси тиску та видатку в
кінці перерізу трубопроводу при прямому пуску двигуна.
0
0,1
0,2
0,3
0,4
0,000 0,015 0,030 0,045 0,060 0,075
Рис.10.7. Високочастотні коливання Гіббса в комунікаційній мережі
241
