Чорний О.П., Луговой А.В. и др. Моделювання електромеханічних систем
Подождите немного. Документ загружается.


З аналізу рівняння кутової характеристики, графік якої
наведений на рис.6.2., випливає:
− реактивний момент
збільшує крутизну
робочої ділянки
кутової
характеристики і
незначно підвищує
перевантажувальну
здатність двигуна;
M
max
M
π
π
/2
θ
Рис.6.2. Кутова характеристика
явнополюсного синхронного
двигуна
− реактивний момент
залежить від квадрата
напруги;
− синхронний момент
лінійно залежить від
напруги.
Це означає, що робочу ділянку кутової характеристики
можна замінити лінійною залежністю, що проходить
через точку номінального режиму:
()
θ= fM
M
M
b
н
н
==
θ
θθ, (6.14)
для
MM< 09.
ma
x
Диференціюючи, одержимо наближене рівняння динамічної
механічної характеристики
(
dM
dt
b
=−ωω
0
)
. (6.15)
З урахуванням останнього рівняння для кутової механічної
характеристики можна записати:
(
)
MM M b
син асин
=+ =+−θβω ω
0
, (6.16)
де
b
M
н
н
=
θ
,
0k
k
s
M
ω
=β
.
Тепер оскільки
145
()
(
θωωt
t
=−
∫
0
0
)
dt, (6.17)
а
()
θ
ω
ω
p
p
=
−
0
(6.18)
то
() ()
()()
Mp b p
b
p
=+−=−+
⎛
⎝
⎜
⎞
⎠
⎟
θ βωω ωω β
00
. (6.19)
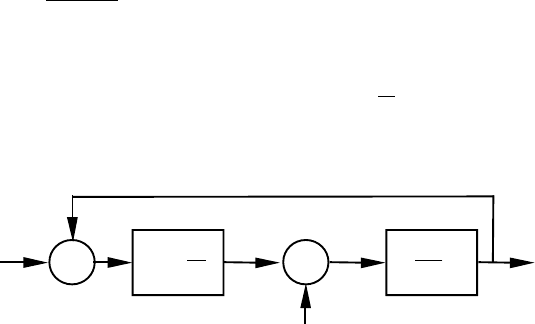
Додаючи до рівняння (6.19) рівняння руху ротора побудуємо
структурну схему лінеаризованої моделі СД (рис.6.3).
(
)
−
(
)
−
M
c
M
β+
b
p
ω
0
ω
1
Jp
Рис.6.3. Структурна схема лінеаризованої моделі СД
6.3. Моделювання синхронних машин у 3-фазній системі
координат
Синхронна машина (СМ) є найскладнішою електричною
машиною в плані моделювання через наявність на роторі
однофазної обмотки збудження і, в окремих випадках, пускової
(демпферної) обмотки.
Існують різні моделі і схеми заміщення, однак при
дослідженнях не враховують другорядні явища і вважають:
− магнітне поле в зазорі розглядається як плоскопаралельне;
− якір береться гладким;
не враховується викривлення поля;
крива поля вважається синусоїдальною; магнітна вісь
обмотки збудження співпадає з повздовжньою віссю машини;
− магнітні осі фазних обмоток зсунуті на 120
P
0
P
; нехтують
полями вищих гармонік і моментами від цих полів;
146
− розподіл струмів у демпферній обмотці синусоїдальний;
− не враховується вплив вихрових струмів і гістерезису;
− не враховується вплив насичення;
− фазні обмотки мають однакові параметри.
Дійсно, через спеціальну форму полюсного наконечника і
робочу точку, що знаходиться, як правило, на вигині
характеристики холостого ходу, відхилення від синусоїдальності
має місце, але не перевищує 5%.
При
складанні системи диференційних рівнянь усі
параметри приводять до системи відносних одиниць (в.о.), що
аналогічна системі в.о. АД. Додатково вводяться:
− відносне значення опору обмотки збудження
r
IR
UI
f
ff
фф
=
2
3
; (6.20)
− інерційна стала
HJ
Pp
j
б
=
ω
0
3
2
. (6.21)
При цьому рівняння якірного кола машини записуються у
вигляді:
UIR
d
dt
UIR
d
dt
UIR
d
dt
AAs
A
ВВs
В
CCs
C
=+
=+
=+
⎧
⎨
⎪
⎪
⎪
⎩
⎪
⎪
⎪
ψ
ψ
ψ
;
;
,
(6.22)
а рівняння обмотки збудження -
Uir
d
dt
fff
f
=+
ψ
. (6.22)
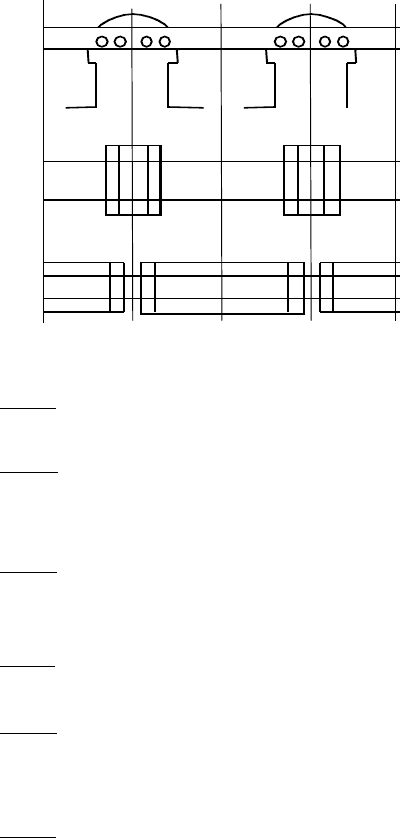
Демпферна обмотка подається у вигляді окремих контурів,
розташованих по двох осях симетрії машини (рис.6.4.).
147
q
d
q
2
d
1
d
1
d
2
d
d
q
2
d
1
d
1
d
2
d
1
q
2
q
2
q
1
q
1
q
2
q
2
q
1
q
Рис.6.4. Зображення розгорнутого демпферного контуру
Для повздовжньої осі машини «d»:
0
0
0
1
11 1 12 2 1
2
21 2 22 2 2
122
=+ + +++
=+ + +++
=+ + +++
⎧
⎨
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
d
dt
ri ri ri
d
dt
ri ri ri
d
dt
ri ri ri
d
d d d d nd nd
d
d d d d nd nd
nd
n d nd n d d nnd nd
ψ
ψ
ψ
... ;
... ;
............................
... .
(6.23)
Для поперечної осі «q»:
0
0
0
1
11 1 12 2 1
2
21 2 22 2 2
122
=+ + +++
=+ + +++
=+ + +++
⎧
⎨
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
d
dt
ri ri ri
d
dt
ri ri ri
d
dt
ri ri ri
q
q q q q nq nq
q
q q q q nq nq
nq
n q nq n q q nnq nq
ψ
ψ
ψ
... ;
... ;
............................
... .
(6.24)
В системах рівнянь (6.23) і (6.24) умовні позначення:
- відповідно потокозчеплення і струм -го ψψ
nd nd nq nq
i,, ,i n
148
демпферного контуру по повздовжній і поперечній осям;
- активний опір -го демпферного контуру струму
цього контуру по поздовжній і поперечній осям;
-
активний опір
i -го контуру струму n -го контуру.
rr
nnd nnq
, n
rr
ind inq
,
Рівняння для потокозчеплення:
ψ
ψ
ψ
ψ
ψ
A A A AB B AC C Af f Ad ed Aq eq
B BA B B BC C Bf f Bd ed Bq eq
C CA CB B C C Cf f Cd ed Cq eq
ed dA dB B dC C ed f ed ed
eq qA qB B qC C eq eq
Li Mi M i Mi Mi Mi
Mi Li Mi Mi Mi Mi
M Mi Li Mi Mi Mi
Mi Mi Mi Mi Li
Mi Mi Mi Li
=+ + + + +
+++ +
+++ +
+++
++
⎧
;
;
;
;
.
⎨
⎪
⎪
⎪
⎩
⎪
⎪
⎪
A
A
A
A
i
=+
=+
=+
=+
(6.25)
Рівняння для електромагнітного моменту:
Mp
W
i const
=
=
∂
∂γ
, (6.26)
де
()
Wiiiiii
A A B B C C f f td ed eq eq
=+++++
1
2
ψψψψψ ψ, (6.27)
та рівняння руху:
J
d
dt
MM
c
ω
=−
. (6.28)
У наведених рівняннях
- взаємні індуктивності
обмоток
M
xy
x
і
y
, - власна індуктивність; індекси «ed » і «eq »
відносяться до демпферних контурів, «
» - до обмотки
збудження.
L
f
Розглянемо визначення індуктивностей і взаємних
індуктивностей обмоток статора. Індуктивності обмоток статора
є періодичними функціями кута між магнітною віссю фази і
поздовжньою віссю «
d » із періодом, рівним
π
(рис.6.5).
149
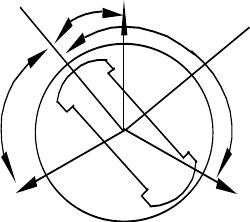
dq
A
C
B
γ
в
γ
a
,
γ
γ
c
Рис.6.5. До визначення індуктивностей обмотки статора
Lll l
Lll l
Lll l
AA
BB
A
B
C
C
C
=
+
+
+
=+ + +
=+ + +
02 4
02 4
02 4
24
24
24
cos cos ...
cos cos ...
cos cos ...
γγ
γγ
γγ
(6.29)
При прийнятих припущеннях досить враховувати не більше
двох складових:
Lll
Lll
Lll
AA
BB
C
C
=
+
=+
=+
02
02
02
2
2
2
cos ;
cos ;
cos .
γ
γ
γ
(6.30)
Підставивши значення кутів (рис.6.5), одержимо
(
()
,3/22cosllL
;3/22cosllL
;2cosllL
20C
20B
20A
π−γ+=
π+γ+=
)
γ
+
=
(6.31)
де
- середнє значення індуктивності фазної обмотки; -
амплітуда зміни індуктивності.
l
0
l
2
Для неявнополюсних синхронних машин
l
2
0
=
;
LLLlcons
A
t
B
C
==
=
=
0
.
Взаємні індуктивності є парними періодичними функціями
кута між віссю «
d » і лінією, проведеною між магнітними осями
розглянутих фаз (рис.6.6).
150
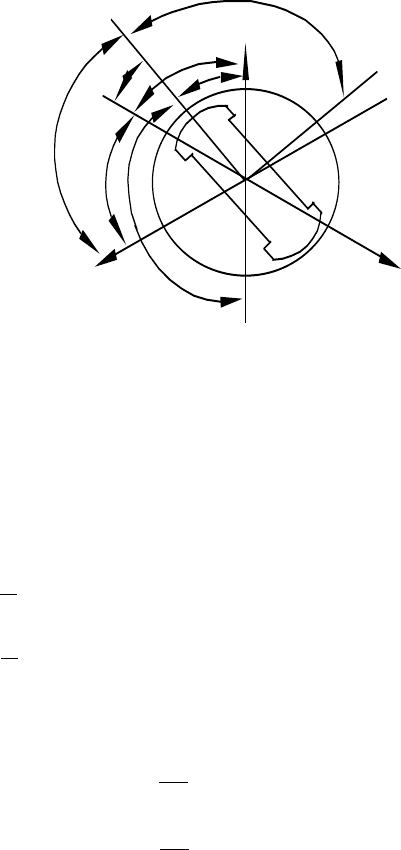
d
q
A
C
B
γ
aс
γ
вc
π
/
3
π
/
3
γ
aв
γ
2
π
/
3
-
γ
Рис.6.6. До визначення взаємних індуктивностей обмоток
статора СД
Наприклад, взаємна індуктивність
M
A
B
буде парною
функцією кута
γ
A
B
Mmm
A
B
A
B
=
+
02
2cos
γ
,
де
- постійна складова взаємної індуктивності, -
амплітуда зміни взаємної індуктивності, причому
m
0
m
2
ml
22
=
.
Враховуючи, що кути
γ
π
γ
γ
π
γ
γπγ
AB
AC
BC
=−
=+
=−
3
3
;
;
,
(6.32)
одержимо
Mml
Mml
Mml
AB
AC
BC
=+ −
⎛
⎝
⎜
⎞
⎠
⎟
=+ +
⎛
⎝
⎜
⎞
⎠
⎟
=+
02
02
02
2
2
3
2
2
3
2
cos ;
cos ;
cos .
γ
π
γ
π
γ
(6.33)
151

Для неявнополюсных M M M m const
A
B
BC
CA
=
=
=
=
0
.
Взаємні індуктивності між фазами й обмоткою збудження
MM
MM
MM
Af Afd
Bf Afd
Cf Afd
=
=−
⎛
⎝
⎜
⎞
⎠
⎟
=+
⎛
⎝
⎜
⎞
⎠
⎟
cos ;
cos ;
cos ,
γ
γ
π
γ
π
2
3
2
3
(6.34)
де
- взаємна індуктивність обмоток при складанні їхніх
магнітних осей.
M
Afd
Аналогічно запишемо взаємні індуктивності між фазними
обмотками і демпферними контурами:
− для поздовжнього контуру
MM
MM
MM
Ad Aed
Bd Aed
Cd Aed
=
=−
⎛
⎝
⎜
⎞
⎠
⎟
=+
⎛
⎝
⎜
⎞
⎠
⎟
cos ;
cos ;
cos ,
γ
γ
π
γ
π
2
3
2
3
(6.35)
− для поперечного контуру
MM
MM
MM
Aq Aeq
Bq Aeq
Cq Aeq
=
=−
⎛
⎝
⎜
⎞
⎠
⎟
=+
⎛
⎝
⎜
⎞
⎠
⎟
cos ;
cos ;
cos ,
γ
γ
π
γ
π
2
3
2
3
(6.36)
де
M
A
ed
і - взаємні індуктивності фазної обмотки і
відповідно повздовжнього і поперечного демпферного контуру
при збігу магнітних осей роторного контуру й обмотки статора.
M
Aeq
Таким чином, цілий ряд індуктивностей та взаємних
індуктивностей, що визначають потокозчеплення, є
періодичними функціями кута
γ
.
152
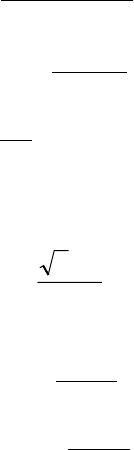
Визначення індуктивностей і взаємних індуктивностей є
дуже складним завданням, оскільки такі дані відсутні навіть у
клієнтському формулярі на двигун. Розрахувати деякі величини
індуктивностей та взаємних індуктивностей можна за такими
формулами:
l
xx x
p
Z
dq c
б
б0
2
2
=
+
+
ω
;
ml
xx
p
Z
dq
б
б22
2
==
−
ω
;
l
m
0
0
2
= ,
індуктивність обмотки збудження:
LrT
ffd
=
′
0
T.
M
U
i
Afd
m
f б
=
2
ω
.
Параметри демпферних контурів:
L
ll
ed
=
+
⎛
⎝
⎜
⎞
⎠
⎟
01
2
02
. ; ; r
ed
= 0 051.
L
ll
eq
=
+
⎛
⎝
⎜
⎞
⎠
⎟
005
2
02
. ; ; r
ed
= 0 021.
Із вищевикладеного можна сформулювати наступні
недоліки моделювання СД у фазних координатах.
1. Рівняння електричної рівноваги містять змінні, що є
функціями кутового положення ротора.
2. Систему диференційних рівнянь не можна подати в
канонічному виді.
3. Одержати рішення системи диференційних рівнянь можливо
тільки чисельно з проміжним рішенням системи алгебраїчних
рівнянь (аналогічно АД).
153

Перелічені недоліки роблять завдання моделювання
синхронної машини дуже складним, у зв'язку з чим
застосовують запис диференційних рівнянь в ортогональній
системі координат «
dq ». ,,0
6.3. Моделювання СМ в ортогональній системі
координат
Істотного спрощення математичної моделі можна досягти за
рахунок застосування перетворення змінних і систем відносних
одиниць. Основним видом перетворення, що застосовується при
моделюванні СМ, є представлення систем диференційних
рівнянь у прямокутній, жорстко зв'язаній з ротором,
координатній системі осей «
dq ». Перетворенню підлягають
струми, напруги і потокозчеплення статора. Рівняння переходу
до ортогональної системи координат мають вигляд аналогічний
рівнянням для АД (5.56), замінюючи
,,0
δ
k
на
γ
:
ii i i
ii i i
dA B C
qA B C
=+−
⎛
⎝
⎜
⎞
⎠
⎟+ +
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
=+−
⎛
⎝
⎜
⎞
⎠
⎟
++
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
⎧
⎨
⎪
⎪
⎩
⎪
⎪
3
2
2
3
2
3
3
2
2
3
2
3
cos cos cos ;
sin sin sin .
γγ
π
γ
π
γγ
π
γ
π
(6.37)
Перетворенню не підлягають змінні рівнянь роторних
обмоток, тому що вони вже зорієнтовані по осях
. dq,
Якщо замінити відповідно до формул перетворення струми,
потокозчепления і напруги статора в рівняннях СМ, то після
відносно нескладних перетворень одержимо нову систему
рівнянь:
− рівняння електричної рівноваги контурів статора, демпферної
обмотки та обмотки збудження
154
