Чикуров Н.Г. Алгоритмическое и программное обеспечение компьютерных систем управления

Подождите немного. Документ загружается.

130

Запишем уравнения трансформаторов, содержащихся в данной

электрической схеме.

111

111 111

211

121

121 21 1

1011

101

1.1)(),

1.2) ( ) ,

1.3) () () ,

2.1)(),

2.2) ( ) ,

2.3) () () ,

3.1)(),

3.2) ( ) ,

3.3) ()

Rax

Ray

TRkM

T kV

TkkV

TRkM

T kV

TkkV

TPkM

T kV

× j=

w× j=

w× j + j ×w=

× j=

w× j=

w× j + j ×w=

× j=

w× j=

w×j

0111

(),

+ j ×w=

где

11 11 211

21 11111

() cos (),

() sin ().

krk

j =- × j ×w =- j ×w

j = × j ×w = j ×w

Дифференциальные уравнения звеньев первой подсистемы.

1),

2).

w =w

j = -w

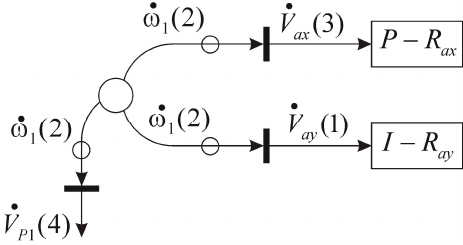
Рассмотрим карту токов первой подсистемы (рис.5.11).

Рис. 5.11

131

Карта токов включает источник тока

и приемник тока

, через которые подсистема 1 и подсистема 2 обмениваются

значениями производных токов

, а также значениями э. д. с.

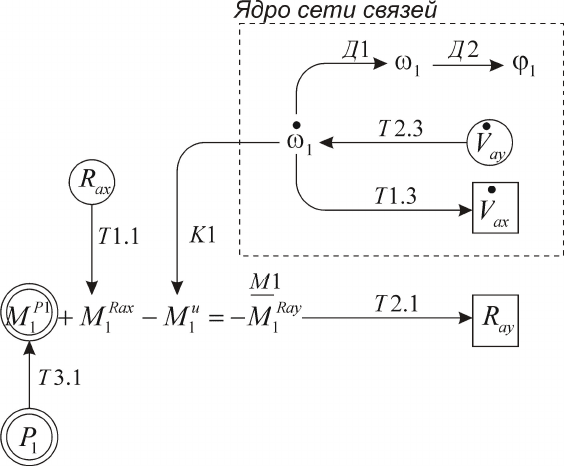
Далее строим сеть связей (рис. 5.12).

Рис. 5.12.

Данная сеть связей состоит из двух частей: ядра и оболочки.

Ядро сети связей включает связи между потоковыми переменными,

т.е. токами и ускорениями токов. Оболочка сети связей

устанавливает связи между потенциальными переменными, куда

входят напряжения и э. д. с. Такое разделение сети связей на две

составляющие будет использовано позже для построения

кинематических моделей механизмов.

Ядро сети связей имеет входную переменную

и выходную

переменную

. Для оболочки входной переменной является

переменная

, а выходной переменной – переменная

На основе сети связей, как и в предыдущем случае, записываем

реестр линейных алгебраических уравнений. Этот реестр является

продолжением реестра предыдущей подсистемы 2.

132

27 111 111

28 211

29 1 121 211

30 1 17

31 1 18

321 111101

331

1.3 () () 0,

2.1 ( ) 0,

2.3 () () 0,

1 ( ),

2.1

ax ax

Ray

ay ay

Ray Rax Ray u

Rax

UVT kkV

URT RkM

UT kkV

UДY

UM M MMMPk

UMTR

=® w×j+j×w-=

=® ×j-=

=w® w×j+j×w-=

=w® w=

=j® j=

= ® + - =-×j

=®

111

34 1 1 11

( ) 0,

1 0.

Rax

U M K MJ

×j-=

= ® - ×w=

(5.13)

Дифференциальные уравнения интегрирующих звеньев

подсистемы 1 имеют следующий вид:

1 1 7 29

1 1 8 30

p pYU

w=w=

j =-w =-

(5.14)

Коэффициенты трансформаторов электрической схемы.

01 18

11 18

21 18

11 11 87 217

21 11 87 117

( ) cos cos ,

() sin sin,

( ) cos cos ,

( ) cos cos ( ) ,

( ) sin sin ( ) .

k r rY

k r rYYkY

j=×× j=××

j=× j=×

j =- × j ×w =- × × =- j ×

j=× j×w=× × = j×

Матрица коэффициентов системы линейных уравнений для

первой подсистемы.

27,29 1 1 27,30 1 1 27,27

28,28 2 1 28,32

29,29 2 1 29,30 2 1 29,26

(), (), 1,

( ), 1,

( ), ( ), 1,

akaka

aka

akaka

= j = j =-

= j =-

=j =j =-

133

30,30

31,31

32,33 32,32 32,34

33,25 1 1 33,33

34,34 34,29 1

1, 1, 1,

( ), 1,

1,.

aaa

aka

a aJ

= = =-

= j =-

= =-

(5.15)

Вектор свободных членов системы линейных уравнений.

307

318

32 101

( ),

B Pk

=-×j

(5.16)

При программировании задачи надо объединить одноименные

группы параметров отдельных подсистем: реестры уравнений (5.5,

5.9, 5.13), матрицы коэффициентов (5.7, 5.11, 5.15), векторы

свободных членов (5.8, 5.12, 5.16) и дифференциальные уравнения

интегрирующих звеньев (5.6, 5.10, 5.14).

Выберем значения исходных параметров модели:

1 2 12

11 22

0.03

0.1, , 10, 20, 1, 2,

, , 0.05.

r l P P mm

JmJmR

== = = ==

=× =×=

Зададим начальные условия для решения системы

дифференциальных уравнений.

12346281

0, 0, , 0, , .

b b bx by

YXYYYVkYVYY

=========j= =j=

Далее вычисляем начальные значения коэффициентов передачи

трансформаторов.

134

12 26

22 26

11 18

21 18

( ) sin sin ,

( ) cos cos ,

( ) sin sin ,

( ) cos cos .

k l lY

k r rY

j =× j=×

j=× j=×

Теперь определим начальные значения угловых скоростей

. Значения этих скоростей можно найти, если численно решить

систему линейных алгебраических уравнений, которые составляют

ядра в сетях связей первой и второй подсистем. В данном случае

рассматриваемая система линейных уравнений достаточно проста и

поэтому имеет аналитическое решение.

21 11

12 21 11 21

22 12

12 21 11 21

() ()

2 () () () ()

() ()

()() ()()

bx by

kVkV

kk kk

k VkV

k k kk

j× + j×

w=×

j×j+j×j

j× - j×

j×j+j×j

Ниже будет рассмотрена методика построения кинематических

моделей, которые позволяют вычислять линейные и угловые

скорости всех звеньев механизма при помощи компьютера.

Присваиваем начальные значения найденных угловых скоростей

переменным

Результаты моделирования представлены в виде графиков на

рис.5.13 и на рис 5.14.

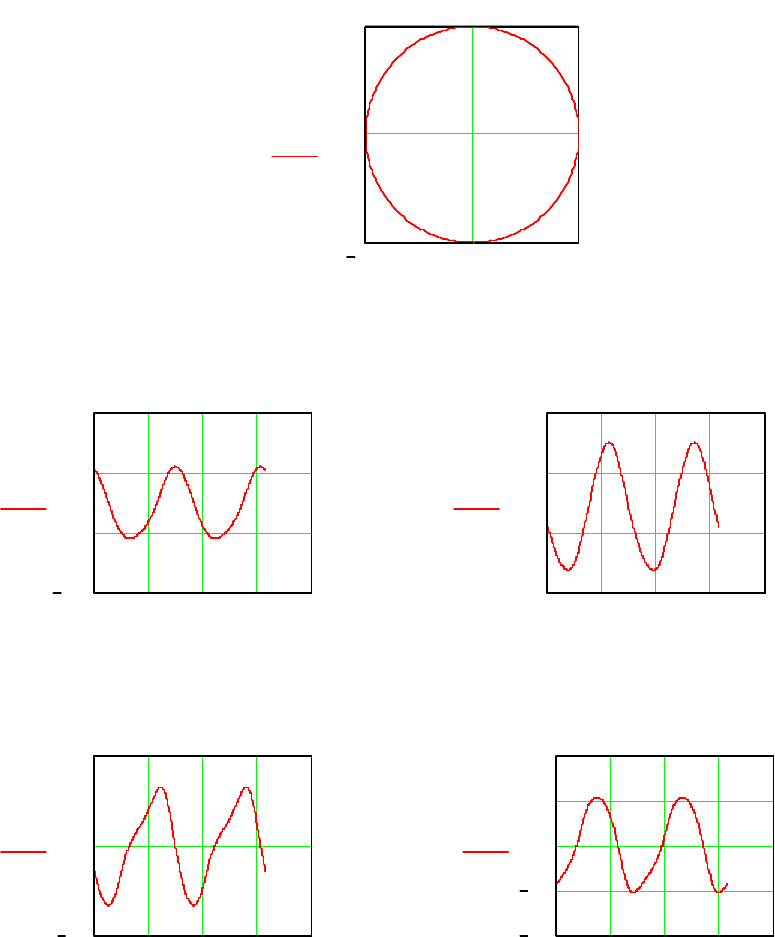
135

0.05 0 0.05

0.05

0.1

Рис. 5.13.

Рис. 5.14.

График на рис. 5.13 показывает ортогональное суммирование

двух движений,

. Результирующее движение совершается по

расчетной траектории, т. е. по дуге окружности. На рис.5.14

представлены графики угловых скоростей

, а также угловых

положений

звеньев 1 и 2.

По заданному движению точки

, принадлежащей звену 2,

рассчитываются абсолютные угловые координаты звеньев.

Следовательно, построенная математическая модель решает

0 0.2 0.4 0.6 0.8

0.5

Fi2

0 0.2 0.4 0.6 0.8

0.5

1.5

Fi1

0 0.2 0.4 0.6 0.8

Y5-

0 0.2 0.4 0.6 0.8

Y7-

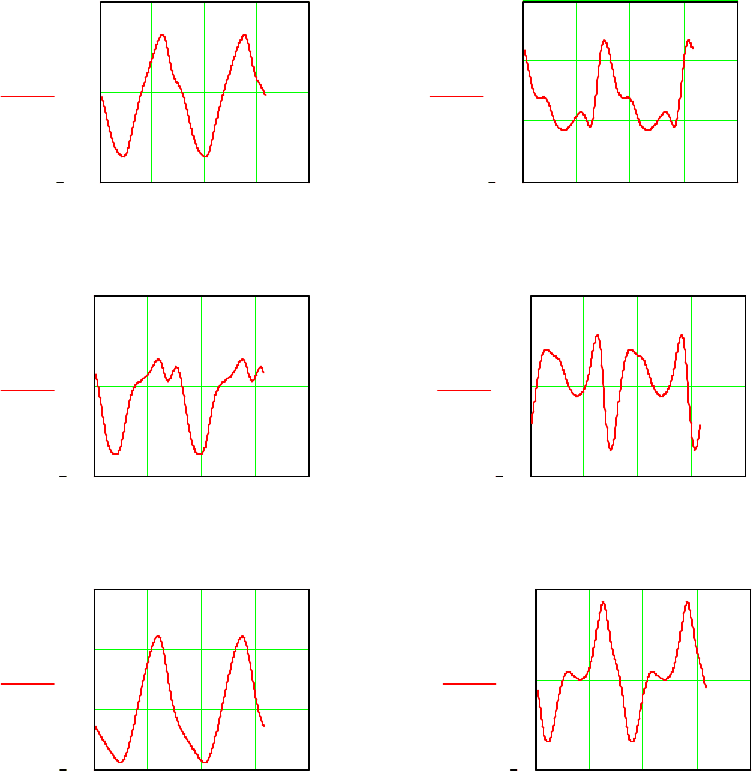
136

обратную задачу робототехники. Параллельно решается первая

задача динамики, когда движение механизма задано и находятся

силы, под действием которых происходит движение механизма.

Рассчитываются линейные и угловые скорости и ускорения звеньев,

значения сил в шарнирах, инерционные моменты и т.д. Общее

количество доступных для наблюдения параметров равно 34.

Графики на рис. 5.15 иллюстрируют динамику изменения некоторых

из них.

Рис. 5.15.

Таким образом, рассмотренная математическая модель – это

сложная динамическая модель. Она позволяет исследовать как

динамические, так и кинематические свойства механизма.

0 0.2 0.4 0.6 0.8

100

Rbx

U15

0 0.2 0.4 0.6 0.8

100

Rby

0 0.2 0.4 0.6 0.8

Rax

U25

0 0.2 0.4 0.6 0.8

Ray

U28

0 0.2 0.4 0.6 0.8

dV2x/dt

U18

0 0.2 0.4 0.6 0.8

dV2y/dt

U10

137

5.2 Кинематическая модель робота в плоскости

Вернемся к предыдущей динамической модели упрощенного

манипуляционного робота (5.1). Сеть связей динамической модели

включает в себя два компонента: независимое ядро и окружающюю

ядро оболочку [18] (см. рис. 5.8 и рис.5.12). Ядро сети связей

образуют уравнения, которые связывают между собой потоковые

переменные (токи и производные токов). Эти уравнения не зависят от

потенциальных переменных (напряжений и э. д. с.) и представляют

собой самостоятельную кинематическую модель. Оболочка,

включающая уравнения для потенциальных переменных, т. е.

напряжений и э. д. с., дополняет кинематическую модель и

превращает ее в динамическую модель. Таким образом, ядро модели

определяет кинематические соотношения механизма, а оболочка его

динамические свойства.

Если от математической модели ожидают получить только

кинематические зависимости, а динамические характеристики

объекта не нужны, то можно ограничиться более простой

кинематической моделью. Для этого достаточно в исходной

динамической модели отбросить оболочку и оставить ядро. В ядре

производные токов надо заменить токами.

Чтобы показать методику таких преобразований, решим снова

обратную позиционную задачу робототехники с использованием

лишь одной кинематической модели.

Задающая подсистема

Поскольку инерционные компоненты в кинематической модели

отсутствуют, то производные токов можно не вычислять. Поэтому

дифференциальные уравнения (4) в кинематической модели не

используются, а остаются лишь уравнения (3).

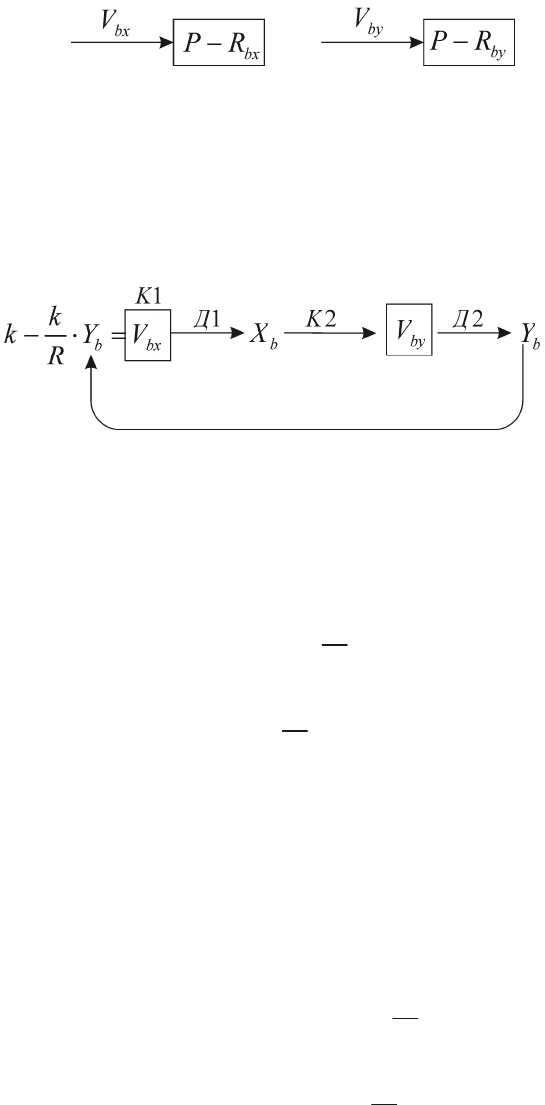
1) ( ),

2).

b bx

b by

D RYV

dtR

dY k

D XV

dtR

=×-=

=×=

138

Все эквивалентные электрические схемы замещения для

кинематической модели и для динамической модели совпадают.

Карты токов для этих моделей отличаются лишь тем, что в картах

токов для кинематической модели вместо ускорений токов

используются токи.

На рис. 5.16 представлена карта токов задающей подсистемы

кинематической модели.

Рис. 5.16

Сеть связей задающей подсистемы упрощается, поскольку не

содержит производных токов (рис. 5.17).

Рис.5.17

Запишем компонентные уравнения, которые используются в

задающей подсистеме.

1),

2).

b bx

b by

Kk YV

K XV

-×=

×=

Составляем реестр уравнений задающей подсистемы.

2 0.

bx b bx

by b by

UX Д XY

U Y Д YY

UVK YVk

UV K XV

=®=

= ® - × - =-

=® ×-=

139

Дифференциальные уравнения интегрирующих звеньев

задающей подсистемы:

b bx

b by

pX V pY U

pY V pY U

Матрица коэффициентов системы линейных алгебраических

уравнений:

1,1

2,2

3,2 3,3

4,1 4,4

, 1,

, 1.

=- =-

= =-

Вектор свободных членов задающей подсистемы.

Подсистема 2

Уравнения Кирхгофа для кинематической модели не содержат

производных токов. Для подсистемы 2 эти уравнения имеют

следующий вид:

1.1) 0,

2.1) 0,

3.1) 0,

4.1) 0.

xaxax

x bx bx

y ay ay

y by by

Kp VVV

Kp V VV

--=

-+=

+-=

-+=

Уравнения трансформаторов определяют зависимости только

между токами, протекающими через эти обмотки.