Чикуров Н.Г. Алгоритмическое и программное обеспечение компьютерных систем управления

Подождите немного. Документ загружается.

140

212

222

1.2) ( ) ,

2.2) ( ) ,

3.2) ( ) ,

4.2) ( ) .

T kV

w× j=

Подсистема 2 кинематической модели содержит одно

дифференциальное уравнение.

1).

j = -w

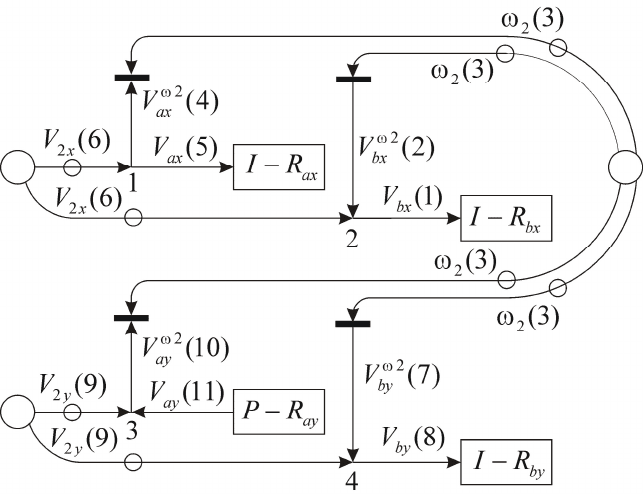
Изображение карты токов подсистемы 2 совпадает с

изображением аналогичной карты токов для динамической модели.

Однако обозначения производных токов на этой карте заменены

обозначениями токов (рис. 18).

Рис. 5.18.

141

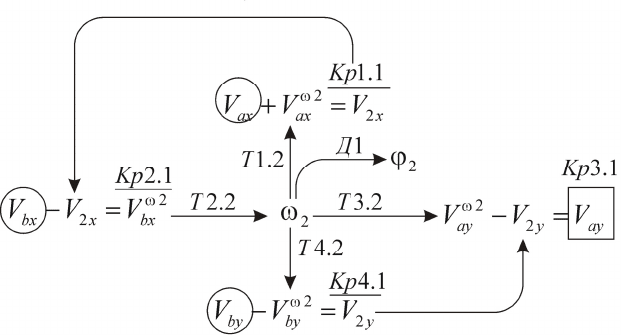
Сеть связей подсистемы 2 кинематической модели представляет

собой ядро сети связей динамической модели (рис. 5.19).

Рис. 5.19.

Далее на основании сети связей записываем, как и ранее, реестр

уравнений подсистемы 2.

5 2 23

622

822

9 212

10 2 212

11 222

1.1 0,

2.1 0,

4.1 0,

1.2 ( ) 0,

2.2 ( ) 0,

3.2 ( ) 0,

x xaxax

bx x bx bx

y y by by

ax ax

ay ay

U ДY

UV Kp VVV

UV Kp V VV

UVT kV

U T kV

UVT kV

=j® j=

=® --=

=® -+=

=® w×j-=

=w® w×j-=

=® w×j-=

222

132

4.2 ( ) 0,

3.1 0,

____________________________________

ay y ay ay

T kV

U V Kp V VV

® w×j-=

=® +-=

=®

Дифференциальное уравнение интегрирующего звена.

2 2 3 10

p pYU

j =-w =-

142

Коэффициенты трансформаторов подсистемы 2.

12 23

22 23

( ) sin sin ,

( ) cos cos .

k l lY

j =× j=×

Матрица коэффициентов системы линейных алгебраических

уравнений.

5,5

6,6 6,14 6,9

7,6 7,3 7,7

8,8 8,4 8,12

9,10 1 2 9,9

10,10 1 2 10,7

11,10 2 2 11,11

2,10 2 2 12,12

13,8 13,13 13,11

1, 1, 1,

( ), 1,

1, 1, 1.

aaa

aka

aaa

= =- =-

==-=

= j =-

= = =-

Вектор свободных членов системы линейных алгебраических

уравнений.

Подсистема 1

Уравнения трансформаторов включают только соотношения

токов.

111

121

1.2) ( ) ,

2.2) ( ) .

T kV

w× j=

143

Дифференциальное уравнение интегрирующего звена

подсистемы 1:

1).

j =w

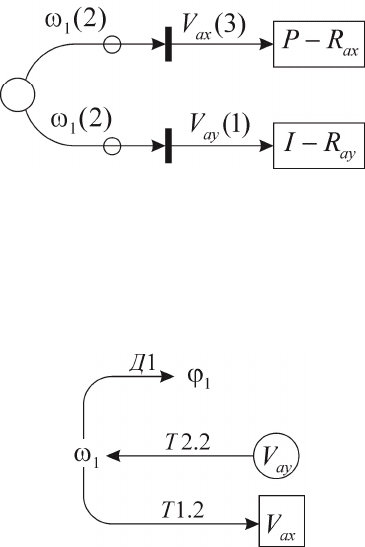
Карта токов подсистемы 1 кинематической модели (рис. 20).

Рис. 5.20

Сеть связей (рис. 5.21).

Рис. 5.21

Реестр уравнений подсистемы 1.

14 111

15 1 121

16 1 14

1.2 ( ) 0,

2.2 ( ) 0,

ax ax

UVT kV

U T kV

UDY

=® w×j-=

=w® w×j-=

=j® j=

Дифференциальное уравнение подсистемы 1.

1 1 4 15

p pYU

j =-w =-

144

Коэффициенты трансформаторов.

11 14

21 14

( ) sin sin ,

( ) cos cos .

k r rY

j=× j=×

Матрица коэффициентов системы линейных алгебраических

уравнений.

14,15 1 1 14,14

15,15 2 1 15,13

16,16

( ), 1,

aka

= j =-

Вектор свободных членов системы линейных алгебраических

уравнений:

164

Исходные параметры кинематической модели примем равными

исходным параметрам динамической модели.

Начальные условия для решения системы дифференциальных

уравнений имеют следующий вид:

1 2 32 41

0, 0, , .

YXYYYY

= = = = =j = =j =

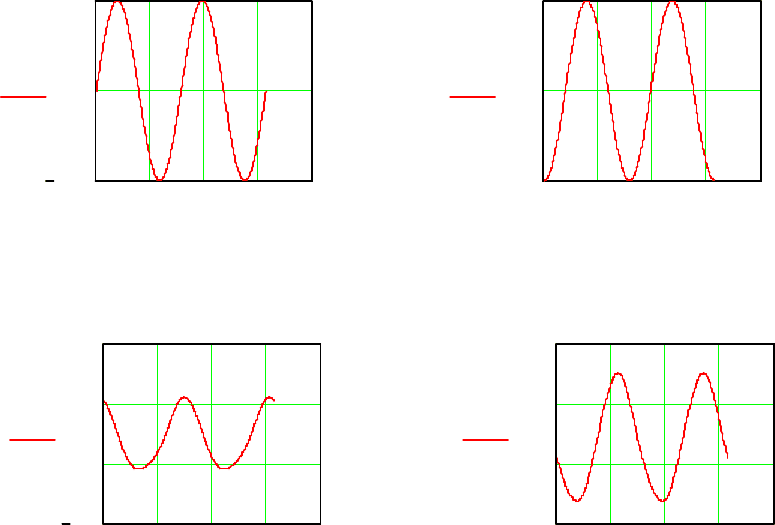
На рис. 5.22 показаны графики изменения переменных,

полученные в результате моделирования кинематической модели.

Эти графики совпадают с аналогичными графиками, полученными в

процессе моделирования динамической модели. Следовательно,

построенная кинематическая модель решает обратную позиционную

задачу робототехники подобно тому, как эту задачу решает

динамическая модель.

По существу кинематическая модель является упрощенной

копией динамической модели, но в отличие от нее может решать

лишь кинематические задачи. Напомним, что с помощью

кинематической модели вычисляются начальные условия для

145

решения дифференциальных уравнений динамической модели. В

этом отношении кинематическую модель можно рассматривать как

важное приложение к динамической модели.

Рис. 5.22.

0 0.2 0.4 0.6 0.8

0.05

0 0.2 0.4 0.6 0.8

0.05

0.1

0 0.2 0.4 0.6 0.8

0.5

Fi2

0 0.2 0.4 0.6 0.8

0.5

1.5

Fi1

146

5.3 Кинематическая модель манипуляционного

робота в 3-мерном пространстве

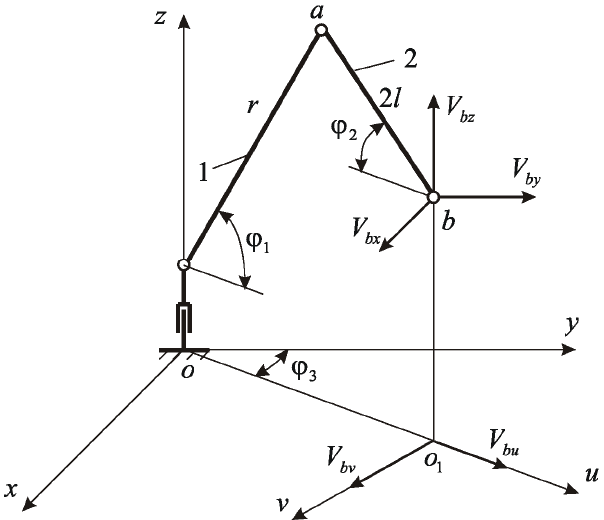
Рассмотрим движение предыдущего двухзвенного механизма в

3-мерном пространстве

Oxyz

(рис. 5.23).

Рис. 5.23

Ориентация звеньев механизма в пространстве определяется

тремя углами:

Решение обратной позиционной задачи

сводится к определению угловых положений

и угловых

скоростей

123

www

звеньев при заданном положении

b bb

xyz

заданных скоростях

bx by bz

VVV

точки

на конце звена 2.

Введем в координатной плоскости

Oxy

подвижную систему

координат

O uv

. Ось

совпадает с проекциями звеньев

на

координатную плоскость

Oxy

, а ось

ортогональна оси

Составляющие вектора скорости точки

вдоль осей

определяются скалярными произведениями векторов.

( ),

bu bx by

bv bx by

=+×

VVu

VVv

(5.17)

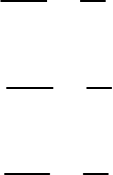
147

где

(

)

( )

0 33

sin,cos,

cos,sin,

,0,

0,.

bx bx

by by

=jj

= j-j

Пусть траекторией, по которой движется точка

, будет

окружность, ориентированная произвольно в системе координат

Oxyz

. Направления скоростей

bx by bz

VVV

соответствуют движению

точки

из начальной точки дуги. Источником движения точки

по

заданной траектории является задающая подсистема. Рассмотрим ее

структуру.

Задающая подсистема

Система дифференциальных уравнений окружности,

ориентированной произвольно в пространстве, имеет следующий

вид:

[ ]

1) ( )( ),

2) ( )( ),

3) ( )( ),

b c b c bx

b c b c by

b c b c bz

dx k

D BzzCyyV

dtR

D CxxAzzV

dtR

D Ay y Bx x V

dtR

= -- -=

где

ABC

– направляющие косинусы нормали к плоскости, в

которой лежит окружность,

c cc

xyz

– координаты центра окружности.

Выделим из системы дифференциальных уравнений

компонентные уравнения.

148

( ) ( )

( )( )

1),

2),

3).

bx bc bc

by bc bc

bx bc bc

KV Bzz Cyy

KV Cxx Azz

KV Ayy Bxx

= ---

éù

ëû

= ---

éù

ëû

= ---

éù

ëû

Чтобы построить эквивалентную электрическую схему

замещения задающей подсистемы, перепишем векторные уравнения

(5.17) в скалярном виде.

3 3 13 23

3 3 23 13

4) sin cos () (),

5) cos sin ( ) ( ),

bu bx by bx by

bv bx by bx by

K V V V Vk Vk

= j+ j=j+j

= j- j=j-j

где

133233

()sin, ()cos.

j= j j= j

С учетом этих уравнений электрическая схема замещения

задающей подсистемы принимает следующий вид (рис. 24).

Рис. 5 24

149

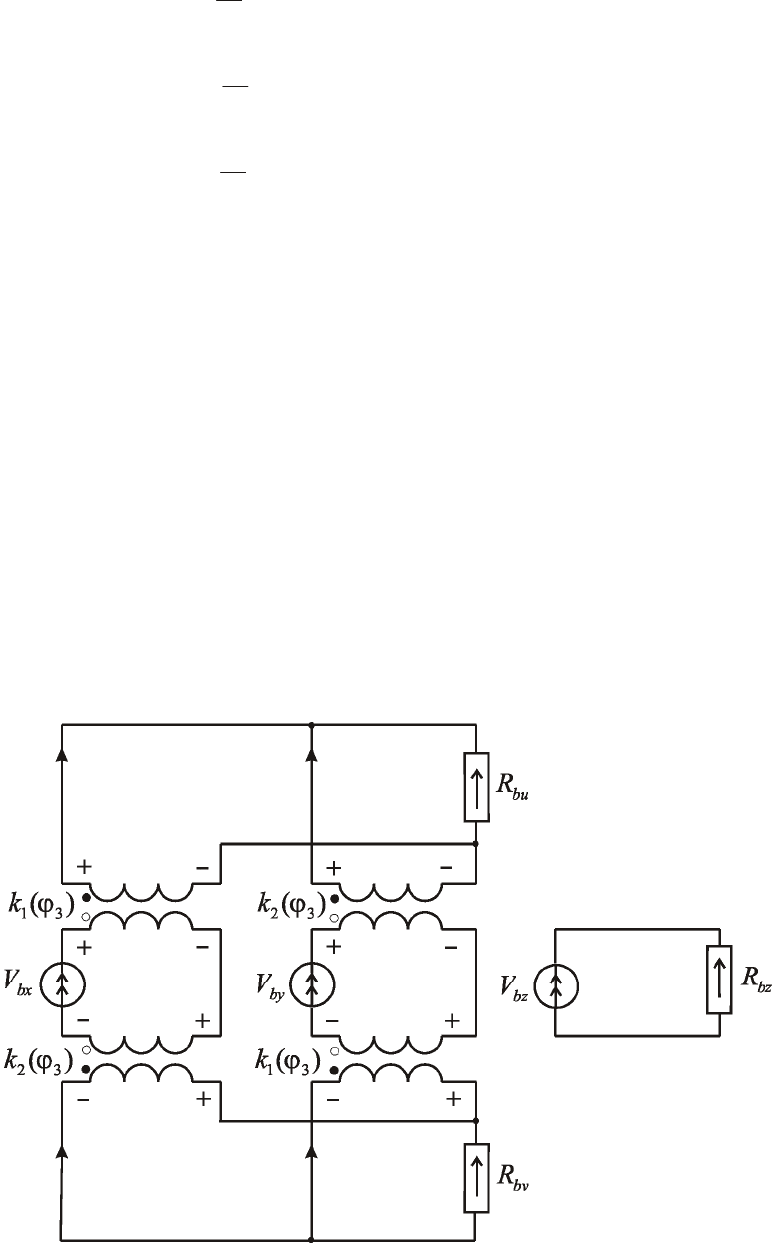
Карта токов (рис.5.25) содержит три приемника токов

bu bv

PRPR

Рис. 5 25

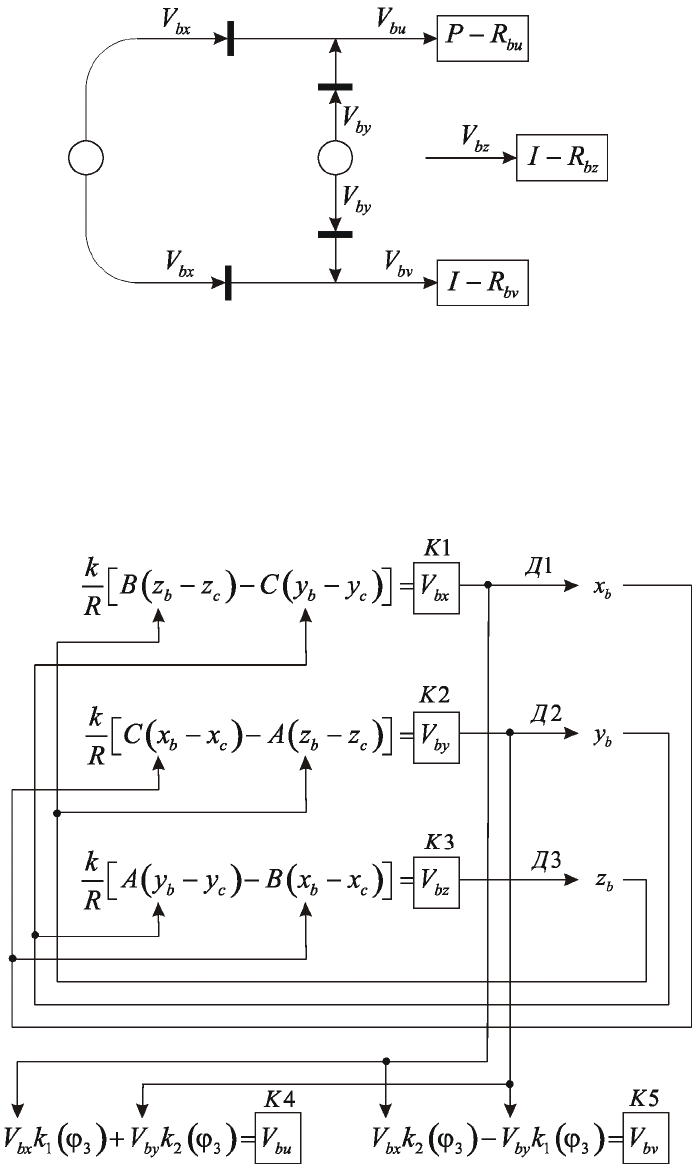
Сеть связей задающей подсистемы (рис.5.26) содержит три

выходные переменные

bx by

Рис.5.26