Чейз, Ричард, Б., Эквилайн, Николас, Дж., Якобе, Роберт, Ф. Производственный и операционный менеджмент

Подождите немного. Документ загружается.

Дополнение к

главе

6. Статистические методы

управления

качеством 211

кальные для каждой комбинации лис, отражают связь ве-

роятности приемки партии продукции с различным про-

центным содержанием брака. Процедура, которой мы сле-

довали при разработке плана выборочного контроля, фак-

тически сводится к определению

двух

точек кривой ОС:

одна из них определяется значением AQL и разностью (1 —

а),

а вторая — показателями LTPD и /3. Данные для по-

строения кривых для наиболее распространенных значений

лис можно вычислить либо взять из специальных таблиц

Построение оперативной характеристики

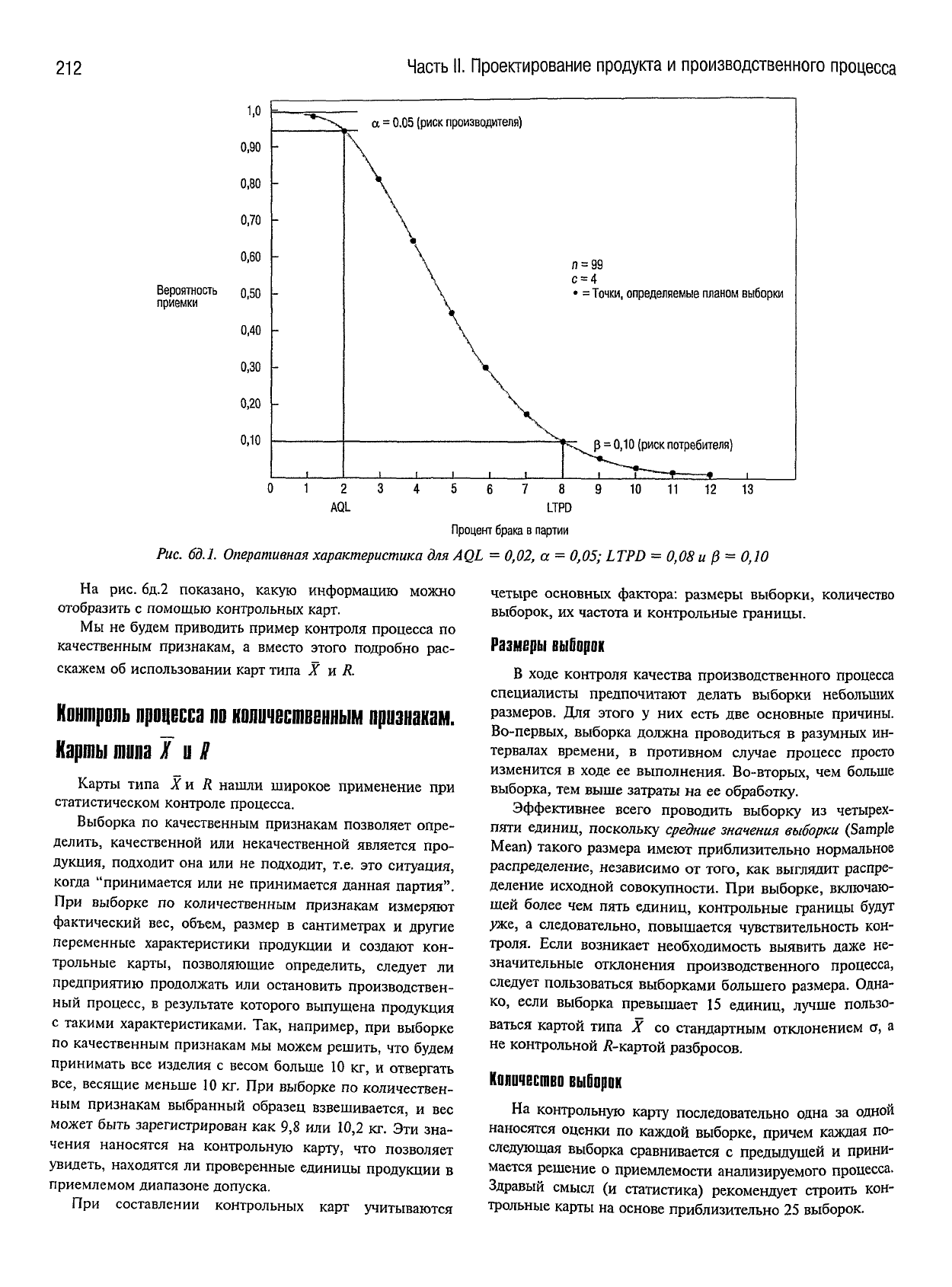
Согласно рис. 6д.1 любой процент бракованных изде-

лий,

отложенный левее 2%-ной отметки,

всегда

будет

приниматься,

а партии, проценты содержания дефектных

-изделий в которых расположены справа от этой отметки,

обязательно

будут

отбраковываться.

Однако построить

такую

кривую можно только в ре-

зультате

100%-ной проверки всей партии, а следователь-

но,

это не осуществимо при реальном плане выборочного

контроля.

Кривая

операционной характеристики должна резко

изгибаться в искомой зоне

(между

AQL и

LTPD),

что дос-

тигается варьированием значений «не. При неизменном

значении

с увеличение размера выборки п приводит к то-

му, что кривая приближается к вертикальной. Если же

неизменным

остается значение п, а значение с (т.е. мак-

симально допустимое число бракованных единиц продук-

ции

в выборке) уменьшается, то наклон кривой также бу-

дет приближаться к более вертикальному, но одновре-

менно

кривая

будет

приближаться к началу координат.

Влияние

размера партии

Размер партии, из которой проводится выборка, отно-

сительно слабо влияет на защиту от приемки некачествен-

ной

партии. Предположим, что из партий самых разных

размеров (от 200 изделий до партии бесконечного размера)

были взяты выборки. Все они одинакового размера и со-

стоят из 20 единиц продукции. Если известно, что каждая

из

этих партий может содержать до 5% бракованных изде-

лий,

то вероятность приемки таких партий при выборке в

20 единиц находится в диапазоне

между

0,34 и 0,36. Это

означает, что, если размер партии

хотя

бы в несколько раз

превышает величину выборки из нее, то он большой роли

не

играет. Это покажется немного странным и сложным

Для восприятия, однако с точки зрения статистики (по

крайней

мере, в среднем)

ответ

будет

практически одина-

ковым,

несмотря на то, какую партию товара вы получили:

целую

машину или одну коробку. Это только кажется, что

из

партии в машине

будет

сделана большая выборка. Одна-

ко

следует

помнить: все это справедливо только при усло-

вии,

что партия выбирается произвольно, и брак распреде-

ляется в ней также случайным образом.

См.,

например, работы Н. F. Dodge and Romig,

Sampling

Inspection

Tablex

—Single

and

Double

Sampling

(New

York:

John

Wiley

& Sons,

1959);

Military

Standard

Sampling

Procedures

and

Tables

for

Inspection

Attributes,

MIL-STD-105D (Washington, DC: U.S. Government Printing

Office,

1983).

Процедуры

контроля

производственного процесса

Контроль процесса связан с отслеживанием ка-

чества непосредственно в

процессе

производства

продукции

или

предоставления

услуги.

Основной це-

лью контроля процесса является снабжение работников

своевременной информацией относительно того,

удовле-

творяет ли произведенная в

ходе

данного процесса продук-

ция

техническим требованиям, а также выявление откло-

нений

в процессе, сигнализирующих о том, что выпущен-

ная

продукция не

соответствует

определенным требова-

ниям.

Фактически контроль процесса часто начинают с

момента, когда начинаются корректирующие мероприятия,

например замена изношенных деталей, капитальный ре-

монт станка или поиск нового поставщика. Различные

концепции

контроля технологического процесса, особенно

контрольные карты, которые строятся на основе статисти-

ческих данных, широко применяются как в производстве,

так и в сфере обслуживания.

Контроль

процесса по качественным признакам.

Карта

типа р

Оценка

по качественным признакам заключается в

оценке

выборки единиц продукции и принятии простого

решения:

данные изделия качественные или некачествен-

ные.

Поскольку это решение типа "Да/Нет", для

приня-

тия

его используются контрольные /?-карты, основанные

на

простых статистических данных, где устанавливаются

верхняя (Upper Control Limit — UCL) и нижняя

(Lower

Control

Limit — LCL) контрольные границы. Эти кон-

трольные границы отмечаются на контрольной карте, а

затем на ней откладываются доли брака каждой отдельно

протестированной выборки. Считается, что анализируе-

мый производственный процесс идет правильно, если вы-

борки,

которые периодически делаются на протяжении

дня,

не

выходят

за пределы указанных контрольных гра-

ниц.

Значения верхней и нижней контрольных границ

рассчитываются по формулам:

— _ Общее число бракованных единиц во

всех

выборках

Количество выборок х Размер выборки '

(бд.1)

(6д.2)

(бд.З)

(6д.4)

где р — доля брака, s

— стандартное (среднеквадрати-

ческое) отклонение, п — размер выборки, a z — количест-

во стандартных отклонений при конкретной степени дос-

товерности. Обычно берутся показатели z = 3 (степень

достоверности —

99,7%)

или z = 2,58 (степень достовер-

ности — 99%).

S „

212

Часть

II. Проектирование продукта и производственного процесса

Вероятность о 50

приемки

1,0

0,90

0,80

0,70

0,60

0,50

0,40

0,30

0,20

010

~*~~\

= 0.05

(риск

производителя)

\ л = 99

= 4

\ • =

Точки,

определяемые

планом

выборки

1 1 1 1

\Р

и,

iu фиск потреоителя;

AQL

11 12 13

LTPD

Процент брака в партии

Рис. 6д.1.

Оперативная

характеристика

для AQL = 0,02, а = 0,05; LTPD - 0,08 и ^ - 0,10

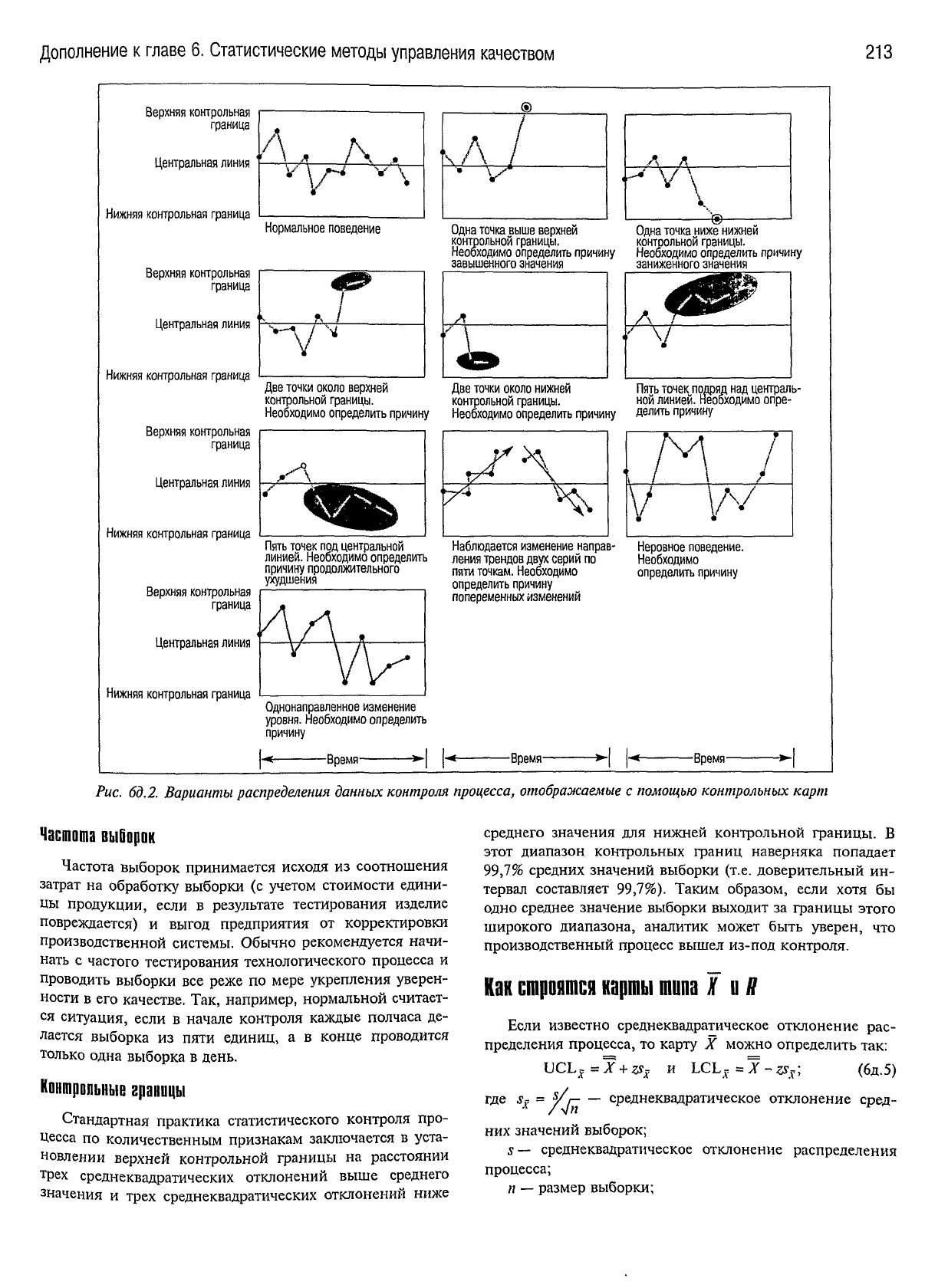
На

рис. 6д.2 показано, какую информацию можно

отобразить с помощью контрольных карт.

Мы

не

будем

приводить пример контроля процесса по

качественным признакам, а вместо этого подробно рас-

скажем об использовании карт типа X и R.

Контроль

процесса по

количественным

признакам.

Карты

типа

и R

Карты типа X и R нашли широкое применение при

статистическом контроле процесса.

Выборка по качественным признакам позволяет опре-

делить, качественной или некачественной является про-

дукция,

подходит

она или не

подходит,

т.е. это ситуация,

когда "принимается или не принимается данная партия".

При

выборке по количественным признакам измеряют

фактический вес, объем, размер в сантиметрах и

другие

переменные характеристики продукции и создают кон-

трольные карты, позволяющие определить,

следует

ли

предприятию продолжать или остановить производствен-

ный

процесс, в

результате

которого выпущена продукция

с такими характеристиками. Так, например, при выборке

по

качественным признакам мы можем решить, что

будем

принимать все изделия с весом больше 10 кг, и отвергать

все, весящие меньше 10 кг. При выборке по количествен-

ным

признакам выбранный образец взвешивается, и вес

может быть зарегистрирован как 9,8 или 10,2 кг. Эти зна-

чения

наносятся на контрольную карту, что позволяет

увидеть,

находятся ли проверенные единицы продукции в

приемлемом диапазоне допуска.

При

составлении контрольных карт учитываются

четыре основных фактора: размеры выборки, количество

выборок, их частота и контрольные границы.

Размеры

выОорок

ходе

контроля качества производственного процесса

специалисты предпочитают

делать

выборки небольших

размеров. Для этого у них есть две основные причины.

Во-первых, выборка должна проводиться в разумных ин-

тервалах

времени, в противном

случае

процесс просто

изменится в

ходе

ее выполнения.

Во-вторых,

чем больше

выборка, тем выше затраты на ее обработку.

Эффективнее всего проводить выборку из

четырех-

пяти

единиц, поскольку

средние

значения

выборки

(Sample

Mean) такого размера имеют приблизительно нормальное

распределение, независимо от того, как выглядит распре-

деление исходной совокупности. При выборке, включаю-

щей более чем пять единиц, контрольные границы

будут

уже, а следовательно, повышается чувствительность кон-

троля. Если возникает необходимость выявить

даже

не-

значительные отклонения производственного процесса,

следует

пользоваться выборками большего размера. Одна-

ко,

если выборка превышает 15 единиц,

лучше

пользо-

ваться картой типа X со стандартным отклонением a, a

не

контрольной Д-картой разбросов.

Количество

выборок

На

контрольную карту последовательно одна за одной

наносятся

оценки по каждой выборке, причем каждая по-

следующая выборка сравнивается с предыдущей и

прини-

мается решение о приемлемости анализируемого процесса.

Здравый смысл (и статистика) рекомендует строить кон-

трольные карты на основе приблизительно 25 выборок.

Дополнение

главе

Статистические

методы

управления

качеством

213

Верхняя контрольная

граница

Центральная

линия

Нижняя контрольная граница

л я

Нормальное поведение

Одна

точка выше верхней

Одна

точка ниже нижней

контрольной границы. контрольной границы.

Необходимо определить причину Необходимо определить причину

Верхняя контрольная

граница

Центральная

линия

Нижняя контрольная граница

Верхняя контрольная

граница

Центральная

линия

Нижняя контрольная граница

Верхняя контрольная

граница

Центральная

линия

Нижняя контрольная граница

завышенного значения

заниженного значения

4Й5^

«=>

Две точки около верхней

контрольной границы.

Необходимо определить причину

Две точки около нижней

контрольной границы. ной линией. Необходимо опре-

Необходимо определить причину делить причину

Пять

точек подряд над централь-

ной линией. Необходимо опре-

•yi

Пять

точек под центральной

линией.

Необходимо определить

причину продолжительного

ухудшения

Наблюдается изменение направ- Неровное поведение,

ления трендов

двух

серий

по Необходимо

пяти точкам. Необходимо

определить причину

попеременных изменений

определить причину

Однонаправленное изменение

уровня. Необходимо определить

причину

-Время-

-Время- -Время-

Рис. 6д.2. Варианты распределения данных контроля

процесса,

отображаемые

помощью

контрольных карт

Частота

выборок

Частота выборок принимается исходя

из

соотношения

затрат

на

обработку выборки

(с

учетом

стоимости едини-

цы

продукции, если

результате

тестирования изделие

повреждается)

выгод предприятия

от

корректировки

производственной системы. Обычно рекомендуется начи-

нать

частого тестирования технологического процесса

проводить выборки

все

реже

по

мере укрепления уверен-

ности

в его

качестве. Так, например, нормальной считает-

ся

ситуация, если

начале контроля каждые полчаса

де-

лается выборка

из

пяти единиц,

а в

конце проводится

только одна выборка

день.

Контрольные границы

Стандартная практика статистического контроля

про-

цесса

по

количественным признакам заключается

уста-

новлении верхней контрольной границы

на

расстоянии

трех

среднеквадратических отклонений выше среднего

значения

трех

среднеквадратических отклонений ниже

среднего значения

для

нижней контрольной границы.

этот диапазон контрольных границ наверняка попадает

99,7% средних значений выборки (т.е. доверительный

ин-

тервал составляет 99,7%). Таким образом, если хотя

бы

одно среднее значение выборки выходит

за

границы этого

широкого диапазона, аналитик может быть уверен,

что

производственный процесс вышел из-под контроля.

Как

строятся карты типа

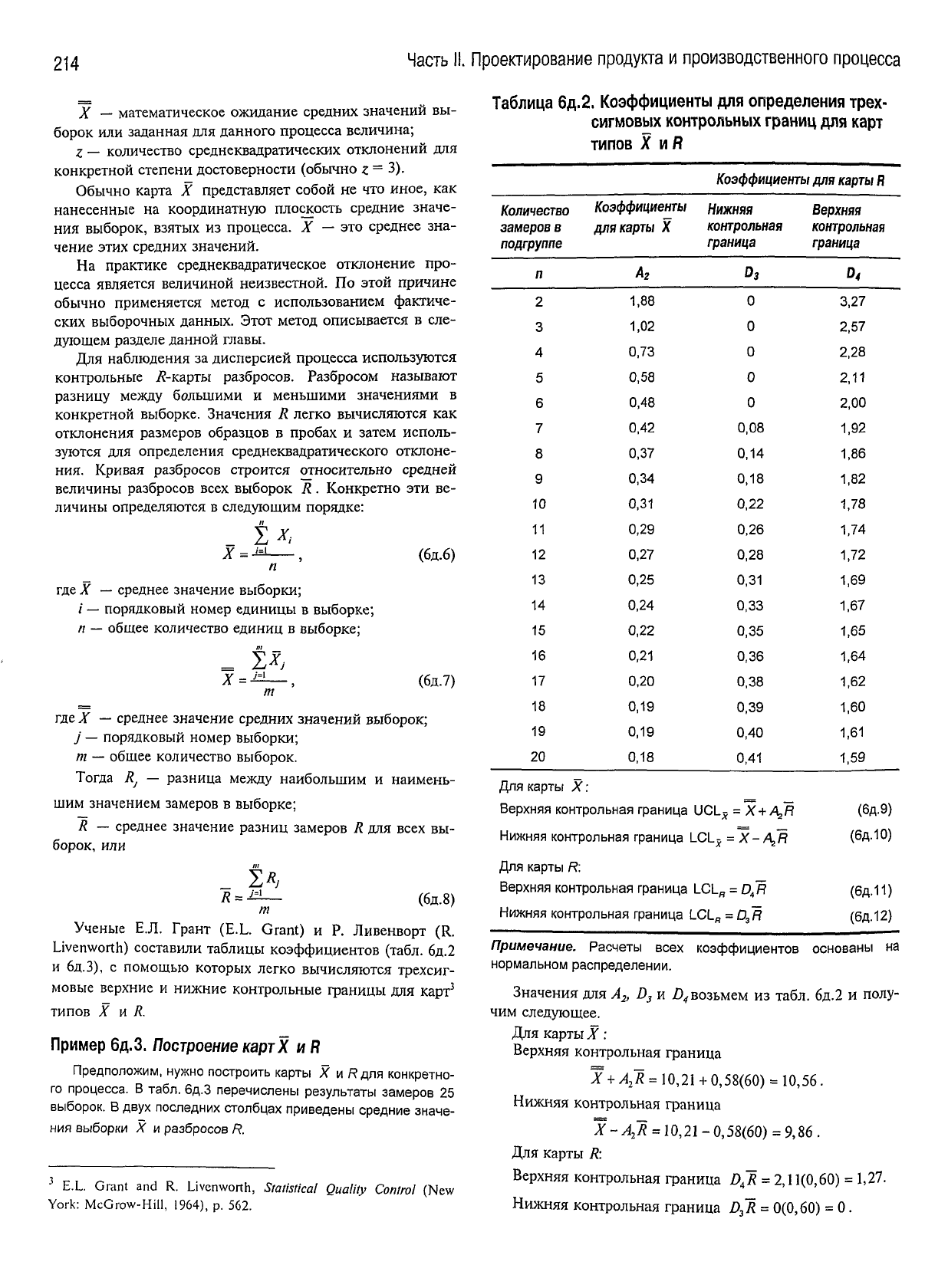
ЕСЛИ

известно среднеквадратическое отклонение

рас-

пределения процесса,

то

карту

можно определить так:

иСЦ = ~Х +

щ и

LCL

~Х

- щ\

(6д.5)

где

= у

\ среднеквадратическое отклонение сред-

них значений выборок;

s — среднеквадратическое отклонение распределения

процесса;

—

размер выборки;

214

Часть

II.

Проектирование

продукта

производственного

процесса

X — математическое ожидание средних значений вы-

борок или заданная для данного процесса величина;

_ количество среднеквадратических отклонений для

конкретной

степени достоверности (обычно z

—

3).

Обычно карта X представляет собой не что иное, как

нанесенные на координатную плоскость средние значе-

ния

выборок, взятых из процесса. X — это среднее зна-

чение этих средних значений.

На

практике среднеквадратическое отклонение про-

цесса является величиной неизвестной. По этой причине

обычно применяется метод с использованием фактиче-

ских выборочных данных. Этот метод описывается в сле-

дующем

разделе данной главы.

Для наблюдения за дисперсией процесса используются

контрольные iJ-карты разбросов. Разбросом называют

разницу

между

большими и меньшими значениями в

конкретной

выборке. Значения R легко вычисляются как

отклонения

размеров образцов в пробах и затем исполь-

зуются

для определения среднеквадратического отклоне-

ния.

Кривая разбросов строится относительно средней

величины разбросов

всех

выборок R . Конкретно эти ве-

личины определяются в следующим порядке:

(6д.6)

где X — среднее значение выборки;

— порядковый номер единицы в выборке;

п — общее количество единиц в выборке;

(6д.7)

где X — среднее значение средних значений выборок;

j — порядковый номер выборки;

т — общее количество выборок.

Тогда Я

— разница

между

наибольшим и наимень-

шим

значением замеров в выборке;

R — среднее значение разниц замеров R для

всех

вы-

борок, или

(6д.8)

Ученые Е.Л. Грант (E.L. Grant) и Р. Ливенворт (R.

Livenworth)

составили таблицы коэффициентов (табл. 6д.2

бд.З), с помощью которых легко вычисляются

трехсиг-

мовые верхние и нижние контрольные границы для карт

типов X и R.

Пример

бд.З.

Построение

картХ

Предположим,

нужно

построить

карты

X и R

для

конкретно-

го

процесса.

табл.

бд.З

перечислены

результаты

замеров

выборок.

двух

последних

столбцах

приведены

средние

значе-

ния

выборки

разбросов

Таблица

6д.2.

Коэффициенты

для

определения

трех-

сигмовых

контрольных

границ

для

карт

типов

Хий

Количество Коэффициенты

замеров

для

карты

подгруппе

1,88

1,02

0,73

0,58

0,48

0,42

0,37

0,34

0,31

0,29

0,27

0,25

0,24

0,22

0,21

0,20

0,19

0,18

Для

карты

Верхняя

контрольная

граница

Нижняяi

контрольная

граница

Для

карты

Верхняя

контрольная

граница

Нижняя

контрольная

граница

Коэффициенты

для

карты

Нижняя

контрольная

граница

0,08

0,14

0,18

0,22

0,26

0,28

0,31

0,33

0,35

0,36

0,38

0,39

0,40

0,41

1ЮЦ

= Х+А,/

LCL^X-V?

LCL

= О

LCL

= D

Верхняя

контрольная

граница

3,27

2,57

2,28

2,11

2,00

1,92

1,86

1,82

1,78

1,74

1,72

1,69

1,67

1,65

1,64

1,62

1,60

1,61

1,59

(6Д.9)

(6Д.Ю)

(бд.11)

(6Д.12)

E.L.

Grant

and R.

Livenworth,

Statistical Quality Control (New

York:

McGrow-Hill,

1964),

p. 562.

Примечание.

Расчеты

всех

коэффициентов

основаны

на

нормальном

распределении.

Значения

для А

, D

и Д, возьмем из табл. бд.2 и полу-

чим

следующее.

Для карты X:

Верхняя контрольная граница

1 = 10,21

0,58(60)

10,56.

Нижняя

контрольная граница

1-4^ =

10,21-0,58(60)

= 9,86.

Для карты R:

Верхняя контрольная граница DJR =

2,11(0,60)

= 1,27.

Нижняя

контрольная граница

0(0,60)

= 0 .

Дополнение

Таблица бд.З.

Номер

выборки

главе

Замеры

10,60

9,98

9,85

10,20

10,30

10,10

9,98

10,10

10,30

9,90

10,10

10,20

10,54

10,20

9,90

10,60

9,90

9,95

10,20

10,30

9,90

Статистические

методы

выборок, состоящих из

управления

пяти единиц

Размер каждой

единицы

выборке

10,40

10,25

9,90

10,10

10,20

10,30

9,90

10,30

10,20

10,40

9,50

10,36

10,50

10,60

10,30

10,60

10,40

9,50

10,30

10,40

9,60

10,20

9,50

10,60

10,30

10,05

10,20

10,30

10,24

10,20

10,40

10,60

10,50

10,20

10,50

10,70

10,50

10,40

10,15

10,60

9,90

10,50

10,30

10,50

9,60

10,30

10,60

9,90

10,23

10,25

9,90

10,50

10,30

10,40

10,24

10,50

10,10

10,30

9,80

10,10

10,30

10,55

10,00

10,80

10,50

9,90

10,40

10,10

10,30

9,80

9,90

качеством

, сделанные

10,20

10,33

10,15

9,95

10,30

9,90

10,10

10,30

10,10

10,20

10,35

9,95

9,90

10,40

10,00

10,50

10,10

10,00

9,80

10,20

10,60

10,20

10,30

9,80

10,10

по

ходу

процесса

Среднее значение

10,28

10,17

10,07

10,09

10,31

10,16

10,12

10,27

10,34

10,30

10,05

10,14

10,28

10,40

10,36

10,29

10,42

9,96

10,22

10,38

10,14

10,23

9,88

10,18

10,16

=10,21

215

Разброс

0,70

0,35

0,40

0,30

0,40

0,50

0,30

0,50

0,40

0,85

0,70

0,80

0,40

0,55

0,60

0,70

1,00

0,80

0,40

1,00

0,55

0,80

0,70

=0,60

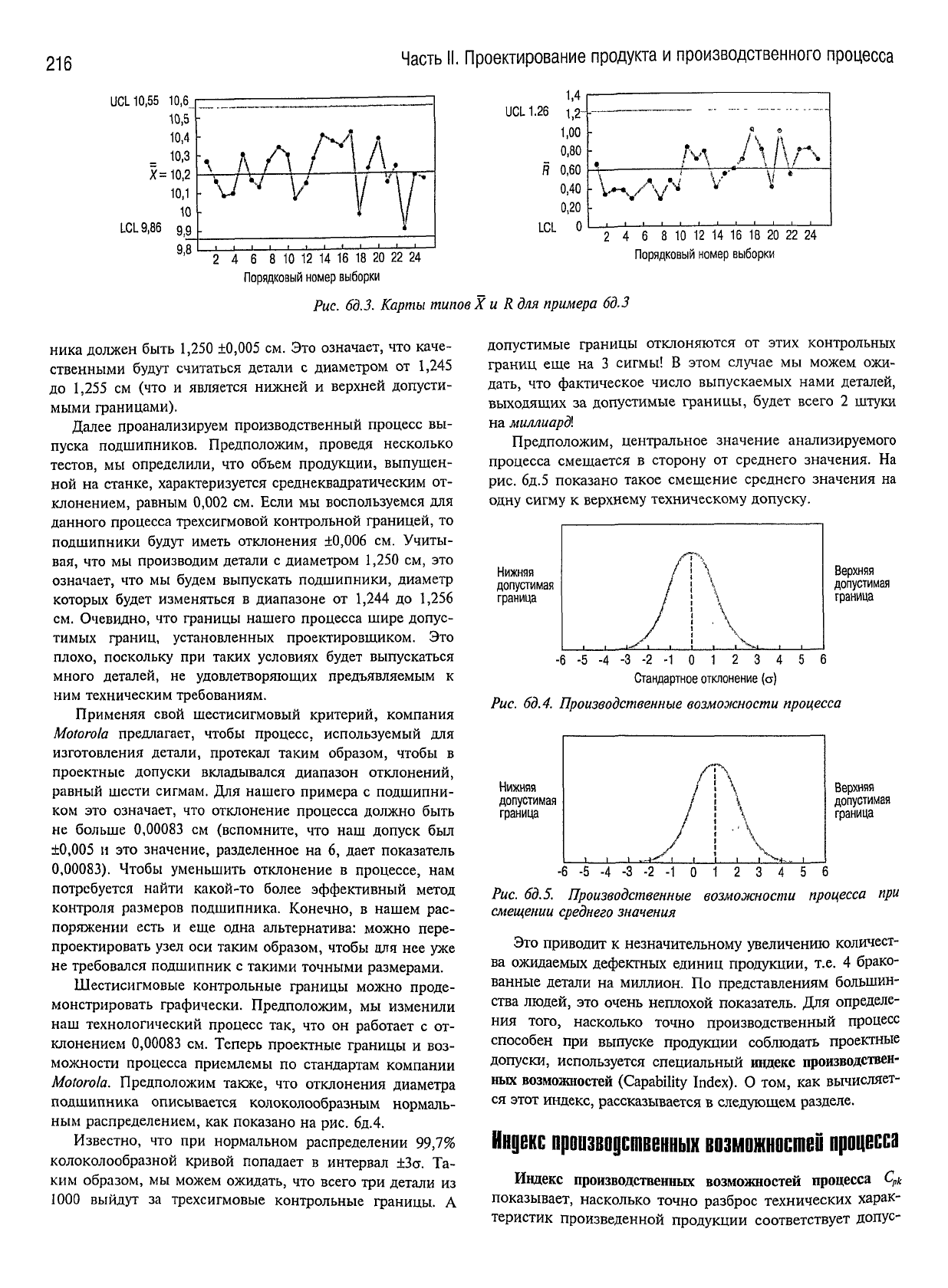
На

рис.

бд.З

изображены карты

X и R с

указанием

всех

средних значений выборок

разбросов выборок.

Обратите внимание,

что все

точки находятся

преде-

лах контрольных границ, однако точка

расположена

очень близко

нижней контрольной границе карты

X .

Производственные

возможности процесса

Приняв

свое время ставшие сегодня широко извест-

ными

шестисигмовые контрольные

границы

(Six-Sigma

Limits),

т.е.

пределы, соответствующие шести среднеквад-

ратическим отклонениям, компания

Motorola

связала

та-

кие

аспекты,

как

производственные возможности процес-

са (Process

Capability)

проектирование продукции. Шес-

тисигмовые границы

— это

сокращенный вариант терми-

на

"границы, соответствующие шести среднеквадратиче-

ским

отклонениям".

При

проектировании

той или

иной

Детали

всегда

оговаривается,

что ее

конкретные размеры

должны оставаться

определенном диапазоне допусков.

Соответствующие проектные границы называют

верхними

нижними техническими допусками

(Upper

and

Lower

Specification

Limits)

или верхними и нижними допустимыми

границами

(Upper

and

Lower

Tolerance Limits

— UTL,

LTL).

Обратите внимание,

что эти

границы

— не

одно

то

же, что

верхние

нижние контрольные границы,

оп-

ределяемые для производственного процесса.

Приведем простой пример. Предположим,

мы

занима-

емся проектированием подшипника

для

вращающегося

вала, скажем,

для оси

автомобильного колеса.

При

этом

нам

необходимо принимать

во

внимание целых

ряд тех-

нических характеристик

как

подшипника,

так и

оси:

ши-

рину подшипника, размер

его

роликов, размер

оси, ее

длину, способ

ее

подвески

и т.д.

Чтобы

все

комплектую-

щие точно соответствовали

друг

другу,

проектировщик

указывает допуски

для

каждого размера. Предположим,

что

законченном проекте указано,

что

диаметр подшип-

216

Часть

II. Проектирование продукта

производственного процесса

UCL 10,55

10,6

4 6 8 10 12 14 16 18 20 22 24

Порядковый номер выборки

UCL1.26

LCL

1,4

1,2-

1,00

0,80

n ac\

0,40

0,20

•

•i.

•vV

6 8 10

Порядковый

A /

2 14 ie

- —

Л/

1»

номер

выборки

...

Рис. бд.З.

Карты

типов

X и R для

примера

бд.З

ника

должен быть 1,250 ±0,005 см. Это означает, что каче-

ственными

будут

считаться детали с диаметром от 1,245

до 1,255 см (что и является нижней и верхней допусти-

мыми границами).

Далее проанализируем производственный процесс вы-

пуска подшипников. Предположим, проведя несколько

тестов, мы определили, что объем продукции, выпушен-

ной

на станке, характеризуется среднеквадратическим от-

клонением,

равным

0,002

см. Если мы воспользуемся для

данного процесса трехсигмовой контрольной границей, то

подшипники

будут

иметь отклонения ±0,006 см. Учиты-

вая,

что мы производим детали с диаметром 1,250 см, это

означает, что мы

будем

выпускать подшипники, диаметр

которых

будет

изменяться в диапазоне от 1,244 до 1,256

см.

Очевидно, что границы нашего процесса шире допус-

тимых границ, установленных проектировщиком. Это

плохо, поскольку при таких условиях

будет

выпускаться

много деталей, не удовлетворяющих предъявляемым к

ним

техническим требованиям.

Применяя

свой шестисигмовый критерий, компания

Motorola

предлагает, чтобы процесс, используемый для

изготовления детали, протекал таким образом, чтобы в

проектные допуски вкладывался диапазон отклонений,

равный шести сигмам. Для нашего примера с подшипни-

ком

это означает, что отклонение процесса должно быть

не

больше

0,00083

см (вспомните, что наш допуск был

±0,005 и это значение, разделенное на 6,

дает

показатель

0,00083).

Чтобы уменьшить отклонение в процессе, нам

потребуется найти какой-то более эффективный метод

контроля размеров подшипника. Конечно, в нашем рас-

поряжении

есть и еще одна альтернатива: можно пере-

проектировать

узел

оси таким образом, чтобы для нее уже

не

требовался подшипник с такими точными размерами.

Шестисигмовые контрольные границы можно проде-

монстрировать графически. Предположим, мы изменили

наш

технологический процесс так, что он работает с от-

клонением

0,00083

см. Теперь проектные границы и воз-

можности процесса приемлемы по стандартам компании

Motorola.

Предположим также, что отклонения диаметра

подшипника

описывается колоколообразным нормаль-

ным

распределением, как показано на рис. 6д.4.

Известно,

что при нормальном распределении 99,7%

колоколообразной кривой попадает в интервал ±3о\ Та-

ким

образом, мы можем ожидать, что всего три детали из

1000

выйдут

за трехеигмовые контрольные границы. А

допустимые границы отклоняются от этих контрольных

границ еще на 3 сигмы! В этом

случае

мы можем ожи-

дать, что фактическое число выпускаемых нами деталей,

выходящих за допустимые границы,

будет

всего 2 штуки

на

миллиард

Предположим, центральное значение анализируемого

процесса смещается в сторону от среднего значения. На

рис.

6д.5 показано такое смещение среднего значения на

одну сигму к верхнему техническому

допуску.

Нижняя

допустимая

граница

Верхняя

допустимая

граница

-6-5-4-3-2-10123456

Стандартное

отклонение

(а)

Рис. бд.4.

Производственные

возможности

процесса

Нижняя

допустимая

граница

t I 1

..~4-^

( (

Верхняя

допустимая

граница

-6-5-4-3-2-10123456

Рис. 6д.5.

Производственные

возможности

процесса

при

смещении

среднего

значения

Это приводит к незначительному увеличению количест-

ва ожидаемых дефектных единиц продукции, т.е. 4 брако-

ванные детали на миллион. По представлениям большин-

ства людей, это очень неплохой показатель. Для определе-

ния

того, насколько точно производственный процесс

способен при выпуске продукции соблюдать проектные

допуски, используется специальный

индекс

производствен-

ных

возможностей

(Capability Index). О том, как вычисляет-

ся

этот индекс, рассказывается в

следующем

разделе.

Индекс

производственных

возможностей процесса

Индекс

производственных

возможностей

процесса

рк

показывает, насколько точно разброс технических харак-

теристик произведенной продукции

соответствует

допус-

Дополнение к главе 6. Статистические методы управления качеством

кам,

определенным проектными границами. Если про-

ектные границы шире

трех

сигм, принятых для процесса,

то среднее значение может немного сдвигаться по отно-

шению к центру, не требуя какое-то время проведения

корректировок процесса, и при этом

будет

продолжаться

выпуск большого процента качественных деталей.

Если вернуться к рис. 6д.4 и 6д.5, то в первом

случае

индекс производственных возможностей процесса С

рк

со-

ответствует

совпадению положения среднего значения

процесса и проектного среднего значения технических

характеристик. В

случае

появления смещения

между

ни-

ми

(см. рис. 6д.5) повышается вероятность выпуска бра-

кованных деталей.

Поскольку среднее значение процесса может смещать-

ся

в любом направлении, направление сдвига и его рас-

стояние от проектных характеристик определяют предел

возможностей процесса, что и отражает индекс производ-

ственных возможностей. С формальной точки зрения,

индекс производственных возможностей С

рк

вычисляется

как

меньшее число из

двух,

определяемых по следующей

формуле:

217

рк

= min

X-LTL

или

UTL-X

Зст

(6д.13)

Для простоты примера предположим, что среднее зна-

чение нашего процесса один сантиметр, а о = 0,001.

Предположим также, что среднее значение процесса на-

ходится точно в центре, как показано на рис. 6д.4. Тогда

при

X = 1,000 получим

рк

min

1,000-0,994

1,006-1,0001

или

3x0,001

0,006

3x0,001

0,003

2 или

0,006

0,003

= 2

Поскольку среднее значение расположено.по центру,

оба вычисления

дают

одинаковый

результат

2. Если бы

оно

сдвинулось на +1,5о (т.е. на

0,0015),

то при

—

1,0015

мы получили бы

"1,0015-0,994

рк

= min

или

1,006-1,000]

3x0,001

min [2,5 или 1,5].

Индекс

рк

в данном

случае

будет

1,5, поскольку это

меньшее из

двух

чисел. Этот индекс говорит нам, что

среднее значение нашего процесса сдвинулось вправо,

как

показано на рис. 6д.5, но детали и теперь выпускают-

ся

в пределах проектных границ.

Предположив, что процесс производит продукцию в

границах ±3о и среднее значение процесса расположено

точно по центру

между

двумя проектными границами,

как

показано на рис. 6д.5, Дэвид Берч (David Birch) вы-

числил доли бракованной продукции, выходящей за пре-

делы различных проектных границ

David Birch, "The True

Value

of 6 Sigma",

Quality

Progress,

April

1993, p. 6.

Проектные

границы

±1a

+2a

±3a

±4a

±5a

±6a

+7a

±8a

Число

забракованных

единиц

продукции

317 на

тысячу

45 на

тысячу

2 на

тысячу

на

миллион

574

на

миллиард

на

миллиард

0,3

на

миллиард

0,001

на

миллиард

Доля

бракованной

продукции

0,3173

0,0455

0,0027

0,000063

0,000000574

0,000000002

0,0000000000003

0,0000000000000001

Шестисигмовые проектные границы компании

Motorola

со смещением процесса от среднего значения на 1,5а

(С

рк

= 1,5)

дают

3, 4 дефекта на миллион изделий. Из при-

веденной выше таблицы видно, что, если среднее значение

находится точно по центру (С

рк

= 2), то можно ожидать два

бракованных изделия на один

миллиард

изделий.

Методы

Тагуши

Мы

обсудили проблему контроля качества с точки

зрения

корректировки технологического процесса. Япон-

ский

ученый Джениши Тагуши (Genichi Taguchi) предло-

жил нововведение, которое сегодня многими считается

настоящей революцией в управлении качеством. По его

предложению вместо непрерывной наладки и переналад-

ки

производственного оборудования, необходимо позабо-

титься о том, чтобы проект продукции был достаточно

хорош для достижения высокого уровня качества в усло-

виях возможных колебаний производственного процесса.

Эта простая идея принята на вооружение такими круп-

ными

компаниями, как

Ford

Motor,

ITT и IBM, которые в

результате

сэкономили миллионы долларов, значительно

сократив издержки производства.

Методы

Тагуши

(Taguchi Methods) — это в основном

статистические методы, предназначенные для поиска

наилучшего сочетания количественных признаков про-

дукции и производственного процесса.

Наилучшее

сочета-

ние означает самые низкие издержки при самой высокой

однородности характеристик продукции.

Поиск

такого

наилучшего сочетания может быть запутанным и дли-

тельным. Так, например, при проектировании технологи-

ческого процесса для выпуска какой-либо новой продук-

ции

можно обнаружить, что только на одном этапе обра-

ботки всего восемь количественных характеристик

процесса (например, скорость работы станка,

угол

резца и

т.д.)

могут

объединяться в

5000

различных комбинаций.

Следовательно, определить комбинацию, в

результате

ко-

торой продукция

будет

характеризоваться наивысшей сте-

пенью однородности при самых низких издержках, не-

возможно, не прибегая к методу проб и ошибок.

218

Часть

II.

Проектирование

продукта

и производственного процесса

Г-н Тагуши нашел способ решения этой проблемы, пред-

ложив сосредоточить внимание на нескольких комбина-

циях,

представляющих весь спектр результатов объедине-

ния

характеристик продукции и процесса.

Сегодня г-н Тагуши широко известен также разработ-

кой

концепции функции потери качества (Quality

Loss

Function

— QLF) для прямой привязки затрат на обеспе-

чение качества к непостоянству производственного про-

цесса. Эта концепция подробно описана в статье

другого

ученого Джозефа Тернера (Joseph Turner), которую мы

обсудим в следующем разделе

Действительно ли

продукция,

не соответствую-

щая

требованиям, им не соответствует?

Непостоянство

качества

Общепринято,

что по мере уменьшения непостоянства

процесса качество повышается. Это можно понять

даже

на

чисто интуитивном уровне. Если поезд всегда приходит во-

время,

можно составить более точный график его движе-

ния.

Если размеры одежды точно соблюдаются, покупатель

может сэкономить время при заказе товаров по каталогу.

Однако о таких вещах редко

думают

с точки зрения стои-

мости низкой степени непостоянства качества. Намного

скрупулезнее это отражается в инженерной сфере. Пор-

шень

должен точно подходить к цилиндру, дверь должна

соответствовать дверному проему, электрические компо-

ненты

должны быть совместимы, а в коробке с

сухим

зав-

траком должно содержаться конкретное количество изю-

минок

— в противном

случае

качество продукции

будет

не-

достаточным, а потребитель разочаруется.

все же именно инженерам отлично известно, что до-

биться нулевых отклонений показателей невозможно. По

этой

причине проектировщики устанавливают конкретные

физические

величины и приемлемые границы их отклоне-

ний.

Так, например, если заданная величина какой-либо

технической характеристики продукции составляет 10 см,

проектная

величина может быть указана как 10,00 см

0,02

см.

Таким образом производственный цех получает ин-

формацию,

что, хотя их целью и является выпуск продук-

ции

с размером точно 10 см, приняты

будут

все изделия в

диапазоне от 9,98 до 10,02 см.

Традиционно

подобные требования трактуются так:

любая деталь, попадающая в дозволенный диапазон, счи-

тается в равной степени качественной, в то время как все

детали, выходящие за рамки дозволенных границ, явля-

ются некачественными. Этот подход наглядно отображен

на

рис. бд.6. Обратите внимание, что в пределах указан-

ного диапазона технических допусков стоимость непосто-

янства

характеристик нулевая, а при

выходе

за его преде-

лы происходит количественный скачок стоимости.

По

мнению г-на Тагуши, такой подход совершенно

лишен

смысла по

двум

причинам.

1. С точки зрения потребителя часто практически не су-

ществует разницы

между

продукцией, точно соответст-

вующей определенным для нее границам технических

допусков, и продукцией, немного выходящей за рамки

этих допусков. И наоборот,

существует

значительное

различие

между

качеством продукции в середине диапа-

зона

допуска и качеством продукции, близкой к грани-

цам

допуска.

2. По мере того как потребитель становится все более тре-

бовательным, необходимость сокращения степени непо-

стоянства качества увеличивается. Однако рис. бд.6 дан-

ной

закономерности не отображает.

Г-н Тагуши предлагает намного более правильную

картину потерь (рис. 6д.7).

Высокая стоимость

Приращение

стоимости

непостоянства

совокупности

характеристик

Нуль

Нижние Заданные Верхние

технические значения технические

допуски

величин допуски

показателей

Рис. бд.6.

Традиционное

видение

стоимости

непостоянства

совокупности

характеристик

Высокая стоимость

Приращение

стоимости

непостоянства

совокупности

характеристик

Нуль

Нижние

технические

допуски

Заданные

значения

величин

показателей

Верхние

технические

допуски

Адаптировано

по статье Joseph

Turner,

"Is an Out-of-Spec Product

Really Out of

Spec?",

Quality

Progress,

December 1900, p. 57-59.

Рис.

6д. 7.

Так г-н

Тагуши

видит

стоимость

непостоянства

совокупности

характеристик

Обратите внимание, что на этом графике стоимость

представлена в виде плавной кривой функции потерь. Су-

ществуют десятки примеров, подтверждающих существова-

ние

такой функции: сцепление колес зубчатой передачи в

коробке

передач, частота смены кадров пленки в фотоаппа-

рате, температура на рабочем месте или в магазине. Прак-

тически по поводу любой измеряемой характеристики по-

требитель ощущает не резкий перепад, а постепенное из-

менение

возможности принять эту продукцию при

приближении

к допустимым пределам, следовательно, его

отношение

к функции потерь более точно характеризуется

графиком,

изображенным на рис. бд.7, а не на рис. бд.6.

Дополнение

главе 6. Статистические методы управления качеством

219

Из

каких элементов состоят эти потери от непостоян-

ства качества? Разные авторитетные источники

отвечают

на

этот вопрос по-разному, однако вначале представляет-

ся

целесообразным отделить внутренние издержки от

внешних. Что касается внутренних издержек, то чем вы-

ше нестабильность производственного процесса, тем

больше

отходов

получается в

результате

производства и

тем больше средств затрачивает компания на проведение

тестов и проверку продукции на соответствие техниче-

ским

требованиям. Когда речь

идет

о внешних издержках,

то,

если качество продукции не приближается к заданно-

му при проектировании уровню, потребители быстро

убеждаются,

что продукция не так долговечна или работа-

ет не так уж хорошо. Возможно, что при использовании в

неблагоприятных условиях продукция вообще не

будет

выполнять

функций, для которых она предназначена, да-

же если изделие полностью

соответствует

техническим

требованиям, разработанным для нормальных условий.

Несмотря

на то, что фактическая форма кривой потерь

может варьироваться довольно сильно, в первом прибли-

жении

ей наиболее

соответствует

простая парабола, по-

добная изображенной на рис. 6д.7, особенно если техни-

ческие допуски симметричны относительно заданной ве-

личины.

Из этой параболы видно, что потери

относительно невелики, если мы предельно близки к за-

данной

величине, и увеличиваются с возрастающей ско-

ростью по мере отклонения от заданной величины.

Если

продукция, не соответствующая установленным

техническим требованиям, постоянно отправляется на

свалку, изгиб кривой потерь в районе заданных величин,

как

правило, становится более крутым, отражая потери на

отходы

и то, что такая продукция никогда не

будет

продана.

Однако во многих практических ситуациях либо в

ходе

производственного процесса выпускается очень высокий

процент

продукции в пределах технических допусков, ли-

бо компания проводит

100%-ную

проверку продукции,

либо продукцию, не

соответствующую

техническим тре-

бованиям,

можно переработать и исправить. В любом из

этих

случаев

наиболее разумным допущением обычно яв-

ляется параболическая функция потерь.

В таких

случаях

применима следующая формула:

K(x-a)

(6д.14)

где

— потери компании, связанные с единицей продук-

ции,

произведенной со значением параметра х;

а — заданная величина показателя; предположим, что

при

а потери L = 0;

—

константа.

Затем добавляем

следующие

переменные для опреде-

ления

К:

с — потери, связанные с единицей продукции, произ-

веденной в пределах технических допусков, при условии,

что потери на единицу при заданной величине показателя

равны

нулю;

d — расстояние от заданной величины показателя до

Установленного технического допуска.

Таким

образом, константа определяется как:

K=c/d

(бд.15)

При

количестве единиц продукции п средние потери

на

единицу составят

-a)

/n].

(6д.1б)

Эта формула позволяет оценить средние потери, но

она

достаточно сложна, поскольку данные обычно соби-

раются такими способами, при которых вычисления на

основе формулы ^(х-а) очень неудобны. Однако в

распоряжении

аналитиков часто есть данные о статисти-

ческом среднем и среднеквадратическом отклонении для

интересующего вас показателя. Если они известны, сред-

нее значение потерь можно с большой степенью точности

вычислить по формуле:

к[сг

(х-а)

(6д.17)

где

— среднее значение процесса;

а — среднеквадратическое отклонение процесса.

Единственная

сложность применения этой формулы в

практических ситуациях связана с правильной оценкой

значения

с, т.е. приростного показателя потерь компании

на

единицу продукции, произведенной в соответствии с

граничными

техническими допусками, по сравнению с

потерями

на единицу продукции, произведенной в соот-

ветствии с заданной величиной показателя. Хотя это зна-

чение в лучшем

случае

может быть только предположени-

ем,

опытные специалисты способны

делать

такие предпо-

ложения

с большой точностью. Одна группа инженеров

предположила, что это значение должно соответствовать

одной

десятой от продажной цены конкретной единицы

продукции. Это означает, что, если технические характе-

ристики

изделия очень близки к граничным допускам,

существует

высокая вероятность, что вследствие непосто-

янства условий тестирования данное изделие может не

пройти

выходной контроль. Более того, велика вероят-

ность того, что потребитель столкнется с большими про-

блемами, пользуясь изделием с граничными характери-

стиками,

чем изделием с характеристиками, соответст-

вующими заданным величинам показателей, и это

приведет к потере данного потребителя и к возможным

возвратам товаров по гарантийным обязательствам произ-

водителя. Хотя такая оценка предположительно носила

несколько

произвольный характер, она представлялась

вполне разумной исходной точкой для выбора методом

минимального числа и в

результате

давала на удивление

точный показатель потерь.

Данный

метод можно проиллюстрировать следующим

примером:

для размеров автомобильной детали были оп-

ределены

следующие

основные технические допуски: 8,5

см

±0,05.

На основе статистических данных известно, что

за последних несколько месяцев средний показатель этого

размера составлял

8,492

см, а среднеквадратическое от-

клонение

0,016 см. Данная

деталь

продается компанией

по

цене 20 долл. за

штуку,

и, по оценке инженеров, если

ее технические характеристики

соответствуют

нижней или

верхней допустимой границе, потери компании на еди-

220

Часть

II.

Проектирование

продукта

производственного процесса

ницу продукции составляют

долл. Компания выпускает

250 тысяч деталей

в год.

Описанная ситуация наглядно

отображена

на

рис.

бд.8.

Нижняя

допустимая

граница

8,450

Среднее

значение

8,495 8,500

Верхняя

допустимая

граница

8,550

Рис. 6д.8.

Пример

распределения

для

автомобильной

детали

Применив

уравнение (бд.17), получаем следующий

средний показатель потерь

на

одну деталь:

[2/(0,05)

][(0,01б)

(0,008)

]

25,6 центов

При

условии ежегодного выпуска

250

тысяч единиц

продукции получаем,

что

общие потери

в год

составят

000

долл. Если инженеры примут решение понизить

эти

потери, они

могут

сделать это тремя способами.

1. Сдвинуть среднее значение

сделать

его

заданной

ве-

личиной

(т.е.

8,5

см).

2. Сократить диапазон отклонений (например, сделать

о-=

0,01).

3. Одновременно предпринять две описанные выше меры.

Воспользовавшись уравнением

(6д.

17)

для

трех

опи-

санный

выше ситуаций, получаем.

При

сдвиге среднего значения

заданному

(1 =

20,5центов), общие потери

в год

составят

51 250

долл.

2. При сокращении диапазона отклонений

до а =

0,01

см

получим

L -13,1

центов

общие потери

в год

составят

32 750 долл.

При

выполнении обоих мероприятий получим

L =

8 центов

общие потери

в год — 20

000 долл.

Обратите внимание,

что

если

для с

указать большее

или

меньшее значение, полученные

результате

показа-

тели изменятся пропорционально. Таким образом,

мы

имеем простую

удобную

возможность провести анализ

чувствительности

для

определенного диапазона значений

с. Так, например, если

бы

значение

было

не 2

долл.,

а 4,

все итоги вычислений были

бы в два

раза больше.

Резюме

Статистический контроль качества

—

тема очень

важ-

ная.

Мы выделили

ее в

дополнение

главе

6, а не

вклю-

чили

саму

главу

вовсе

не

затем, чтобы подчеркнуть

ее

второстепенную роль. Вопросы качества приобрели

в по-

следнее время такое большое значение,

что

статистиче-

ские

процедуры обеспечения качества,

как

правило,

явля-

ются неотъемлемой частью деятельности любой преуспе-

вающей фирмы. Сегодня схемы выборочного контроля и

статистический контроль процесса рассматриваются руко-

водством компаний

как

нечто само собой разумеющееся

внимание уделяется более широкому спектру аспектов

(например,

отказ

от

входного выборочного статистиче-

ского контроля вследствие надежного качества продукции

поставщиков; расширение полномочий служащих, что за-

менило многие аспекты контроля производственного

процесса).

Все

современные производственные компании

мирового класса

требуют

от

своих работников понимания

основных концепций, описанных

данном дополнении.

ООзор

формул

Контроль процесса по качественным признакам. Кон-

трольная карта типа

р:

—

Общее число бракованных единиц

во

всех

выборках

Количество выборок

Размер выборки

(бд.2)

(6Д.З)

(бд.4)

1X1,,

= *-©*

(бд.5)

Контроль процесса по количественным признакам.

Кон-

трольные карты типов

X и R:

LCL

p-zs

(бд.6)

(бд.7)

(бд.8)

Контрольные

границы.

Для

карты

X :

Верхняя контрольная граница UCL^

(6д-9)

Нижняя

контрольная граница

ЪСЦ =*Х-

(бд.10)

Для

карты

Верхняя контрольная граница

ЬСЬ

= DJR. (6Д-П)

Нижняя

контрольная граница

ЬСЬ

(6д.12)

Индекс

производственных возможностей процесса

(6д.13)

(fa. 14)

(бд.15)

(бд.16)

(бд.17)

За

К(х-а)

K=c/d