Черный С.Г., Чирков Д.В. и др. Численное моделирование течений в турбомашинах
Подождите немного. Документ загружается.


ïîëó÷èì ñîîòâåòñòâåííî
∂
∂
∫∫
=
∂
y
y
x
dV dS
V
x
V
,
∂
∂
∫∫
=
∂
y
y
y
dV dS
V
y
V
,
∂
∂
∫∫
=
∂
y
y
z
dV dS
V
z
V
.
(1.142)
Ïåðåõîäÿ â êàæäîé ÿ÷åéêå ñåòêè (ñì. ðèñ. 1.4) ê äèñêðåòíûì àíà
-
ëîãàì ðàâåíñòâ (1.142), íàõîäèì ñîîòíîøåíèÿ äëÿ âû÷èñëåíèÿ ïðî
-
èçâîäíûõ îò ëþáîé ñêàëÿðíîé ôóíêöèè (â òîì ÷èñëå è îò êîìïîíåíò
âåêòîðà ñêîðîñòè) â öåíòðå ÿ÷åéêè:
∂
∂
⎛
⎝
⎜
⎞
⎠
⎟
=−+−
+− +
y
yyyy
q
VS S S
ijk
qi qi qj
() () () (
// /12 12 12
S
SS
qj
qk qk
)
() () .
/
//
−
+−
+
+−
12
12 12
yy
(1.143)
Çíà÷åíèÿ êîìïîíåíò ñêîðîñòè íà ãðàíÿõ ÿ÷åéêè âû÷èñëÿþòñÿ
ïî ôîðìóëàì
yyy
mmm++
=+
12 1
05
/
,( )
. (1.144)
Ñ ó÷åòîì âûïîëíåíèÿ âñåãäà èíòåãðàëüíîãî ðàâåíñòâà
d
V
S =
∂
∫
0
(1.145)
è, êàê ñëåäñòâèå, åãî äèñêðåòíîãî àíàëîãà
SSSSSS
iij jkk+−+−+−
−+−+−=
12 12 12 12 12 12
0
//////
, (1.146)
à òàêæå ñîîòíîøåíèé (1.144) âûðàæåíèÿ äëÿ ïðîèçâîäíûõ îò êîìïî
-
íåíò âåêòîðà ñêîðîñòè (1.143) ìîãóò áûòü óïðîùåíû:
∂
∂
⎛
⎝
⎜
⎞
⎠
⎟
=−+
++ −− +
y
yyy
q
VSSS
ijk
iqi iqi jqj
05
112 112 1
,(
//+
−− ++ −−
−
−+ −
12
112 112 112
/
///
).yyy
jqj kqj kqk
SSS
(1.147)
ßâíî-íåÿâíàÿ àïïðîêñèìàöèÿ èñòî÷íèêîâîãî ÷ëåíà
Ñâîáîäíûå ÷ëåíû â ïðàâûõ ÷àñòÿõ óðàâíåíèé (1.9), (1.13)–(1.15)
k − e
ìîäåëåé èìåþò â îáùåì ñëó÷àå âèä
HG
k
k
y
=−−en2
2
,
HCGC f f
kk
y
ee
e
ee e
n=− −
1
2
2
23
2
2
*
. (1.148)
Ìåòîä ÷èñëåííîãî ðåøåíèÿ òðåõìåðíûõ çàäà÷ äèíàìèêè 71

Äëÿ òîãî ÷òîáû óâåëè÷èòü çàïàñ óñòîé÷èâîñòè ÷èñëåííîãî àëãî
-
ðèòìà (1.134) ðåøåíèÿ
k − e
óðàâíåíèé (1.9), (1.13)–(1.15) (à ñëåäîâà
-
òåëüíî, óñêîðèòü ñõîäèìîñòü èòåðàöèé èëè ÷èñëåííîãî ðåøåíèÿ
ýòèõ óðàâíåíèé ê ñòàöèîíàðíîìó ðåøåíèþ ïîñðåäñòâîì âûáîðà ëþ
-
áûõ ñêîëü óãîäíî áîëüøèõ øàãîâ
Dt
èëè
Dt
), áóäåì âñå âõîäÿùèå
ñþäà ñëàãàåìûå, èìåþùèå îòðèöàòåëüíûå êîýôôèöèåíòû ïðè èñêî
-
ìûõ ôóíêöèÿõ, àïïðîêñèìèðîâàòü íåÿâíî (ò.e. íà
s + 1
-é èòåðàöèè
n + 1-ãî ñëîÿ ïî âðåìåíè).
Ïåðåïèøåì âûðàæåíèÿ äëÿ
H
k
è
H
e
â (1.148) ñëåäóþùèì îáðàçîì:
HG k
k
T
k
y
=− −
1
2
2
n
,
HCGC f f
kT
y
ee
e
ee e
n=− −
1
2
23
2
2
*
, (1.149)
ãäå
Tk= / e
— òóðáóëåíòíûé ìàñøòàá âðåìåíè. Îáû÷íî îí îãðàíè-
÷èâàåòñÿ ñíèçó çíà÷åíèåì
TC
k
T
=
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
max
e
n
e
,
,05
, (1.150)
ãäå
C
T
C
=
2
m
.
Ïîýòîìó êîýôôèöèåíòû
−+(/ / )12
2
Tyn
ïðè
k
â
H
k
è
−+(/ / )CT yf
e
n
2
2
3
2
ïðè
e
â
H
e
ÿâëÿþòñÿ âñåãäà îòðèöàòåëüíûìè.
 ñèëó ýòîãî òîëüêî äàííûå ñëàãàåìûå â ñâîáîäíûõ ÷ëåíàõ àïïðîê
-
ñèìèðóþòñÿ íåÿâíî, à îñòàëüíûå — ÿâíî:
HG k
k
s
s
s
T
y
++
=− +
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
1
2
1
1
2
n
,
HC GC f
s
s
s
s
k
C
T
y
ee
e
e
en
e
++
=
⎛
⎝
⎜
⎞
⎠
⎟
−+
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
1
1
2
2
2
3
1
2
*
. (1.151)
Ñëåäóåò îòìåòèòü, ÷òî â ñâîáîäíûõ ÷ëåíàõ (1.151), êàê è â îñòàëü
-
íûõ ÷ëåíàõ ðàçíîñòíûõ óðàâíåíèé (1.134), ñîñòàâëÿþùèå âåêòîðà
ñêîðîñòè áåðóòñÿ óæå ïîñ÷èòàííûìè íà s + 1-é èòåðàöèè èç óðàâíå
-
íèé íåðàçðûâíîñòè è êîëè÷åñòâà äâèæåíèÿ.
72 Ãëàâà 1
1.3.5. Ëèíåàðèçàöèÿ
Äëÿ ðåøåíèÿ íåëèíåéíîãî óðàâíåíèÿ (1.134) ïðîâîäèòñÿ åãî ëè
-
íåàðèçàöèÿ ïî ìåòîäó Íüþòîíà ñ èñïîëüçîâàíèåì çàïèñè ëèíåàðè
-
çîâàííûõ óðàâíåíèé â äåëüòà-ôîðìå (ò.å. óðàâíåíèå çàïèñûâàåòñÿ
îòíîñèòåëüíî
Dy
sss++
=ϕ −ϕ
11
):
15
1
34
,()
V
t
RHS
s
ss
snn
D
−
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
ϕ−ϕ=−
∂
∂ϕ
ϕ−ϕ+ ϕ
+
−
1
2Dt
VRHS
s
+
. (1.152)
Ïðè ïîñòðîåíèè íåÿâíîãî îïåðàòîðà â ëåâîé ÷àñòè (1.152) ïîëà
-
ãàåòñÿ, ÷òî íà âñåõ ãðàíÿõ íåâÿçêèé ïîòîê àïïðîêñèìèðóåòñÿ ñ ïåð
-
âûì ïîðÿäêîì
[]
{ }
() ()() ||
////
ϕ⋅ = ϕ +ϕ − ϕ
+++++
uS u u S
mmmmmm
U
12 1 12 12 12
1
2
D
, (1.153)
à â âÿçêîì ïîòîêå îñòàâëÿþòñÿ ïðîèçâîäíûå òîëüêî ïî òîé êîîð-
äèíàòå, ïîâåðõíîñòüþ óðîâíÿ êîòîðîé ÿâëÿåòñÿ ðàññìàòðèâàåìàÿ
ãðàíü:
nw w w nw
xhz x
*
/
*
123
12
1
∂ϕ
∂
∂ϕ
∂
∂ϕ
∂
∂ϕ
∂
++
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
=
⎛
⎝
+i
⎜
⎞
⎠
⎟
++
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
=
+
+
∂ϕ
∂
∂ϕ
∂
∂ϕ
∂
i
j
12
123
12
/
*
/
,
nw w w
xhz
nw
nw w w
h
xhz
*
/
*
,
2
12
123
∂ϕ
∂
∂ϕ
∂
∂ϕ
∂
∂ϕ
∂
⎛
⎝
⎜
⎞
⎠
⎟
++
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
+j
⎢
⎤
⎦
⎥
=
⎛
⎝
⎜
⎞
⎠
⎟
+
+
∂ϕ
∂
k
k
12
3
12
/
*
/
.nw
z
(1.154)
Ýòî îçíà÷àåò, ÷òî â ðàçíîñòíûõ ïîòîêàõ óðàâíåíèé (1.134) íåÿâ
-
íî ðàññìîòðåíû òîëüêî ÷ëåíû, óêàçàííûå â ïðàâûõ ÷àñòÿõ ðàâåíñòâ
(1.153) è (1.154), à îñòàëüíûå áåðóòñÿ ÿâíî.
Ó÷èòûâàÿ (1.153) è (1.154), à òàêæå àïïðîêñèìàöèþ èñòî÷íèêî
-
âûõ ÷ëåíîâ (1.151), íàéäåì
∂∂ϕRHS /
è ïåðåïèøåì (1.152) â âèäå
15
12 12 12 12
,
()
// //
*
V
t
MV U U
ii ii
i
D
DD++ + −
⎧
⎨
⎩
−
+
−
+−
+
−
+
nw
x
[]
12 12 12 12 12 12 12//
*
// // /
()DDDD
iiijjj
UU
+−−+
−
+−
+
−++nw
x
[]
j
jj jj k
U
−
++ −− +
−
−
−−+
12
12 12 12 12 12
/
*
//
*
// /
() ()nw nw
hh
DDDD
kkk
U
+−
+
−
+−
12 12 12///
Ìåòîä ÷èñëåííîãî ðåøåíèÿ òðåõìåðíûõ çàäà÷ äèíàìèêè 73

[]
}
−− =
=−
++ −−
+
ϕ−ϕ
() ()
*
//
*
//
nw nw y
zzkk kk
s
s
12 12 12 12
1
34
DDD
nn
s
t
VRHS
+ϕ
−
+
1
2D
,
(1.155)
ãäå
M
Tvy k
CT vfy
=
+
+
12
2
2
23
2
//
//
äëÿ -óðàâíåíèÿ,
äëÿ -óðàâí
e
e åíèÿ.
⎧
⎨
⎩
Äàëåå èäåíòèôèöèðóåì êîýôôèöèåíòû
w
m
m(,,)= 123
òàê æå,
êàê è âåëè÷èíû
U
±
, òîëüêî ïî íèæíåìó èíäåêñó:
ww
ii±±
≡
12 1 12//
()
— êîýôôèöèåíò
w
1
, âçÿòûé íà ãðàíè
S
i±1/2
;
ww
jj±±
≡
12 2 12//
()
— êîýôôèöèåíò
w
2
, âçÿòûé íà ãðàíè
S
j ± 1/2
;
ww
kk±±
≡
12 3 12//
()
— êîýôôèöèåíò
w
3
, âçÿòûé íà ãðàíè
S
k ± 1/2
.
Òîãäà óðàâíåíèå (1.155) ìîæíî ïåðåïèñàòü â áîëåå êîìïàêò-
íîì âèäå
15
12 12 12 12 12
,
// // /
V
t
MV C C C
ii ii j
D
DD D++ +
⎛
⎝
⎜
⎜
+
+
−
+−
+
−+
−
jjj
kk k
k
C
CC
+−
+
−
+
−
+−
+
−
++
++
⎞
⎠
12 12 12
12 12 12
12
///
// /
/
D
DD
⎟
⎟
=− +
+
−
ϕ−ϕ+ ϕ
D
D
y
s
snn
s
t
VRHS
1
1
34
2
,
(1.156)
ãäå
CU mijk
mm m+
±
+
±
+
=±
12 12 12//
*
/
() ,nw =, ,
.
Èç îïðåäåëåíèÿ
w
m
m(,,)= 123
â (1.97) è ñ ó÷åòîì ââåäåííîé
èäåíòèôèêàöèè
w
ïî íèæíåìó äðîáíîìó èíäåêñó èìååì ñëåäóþùåå
âûðàæåíèå äëÿ
w
m+12/
:
w
m
mm
m
V
+
++
+
=
⋅
12
12 12
12
/
//
/
SS
. (1.157)
1.3.6. Ìåòîä LU-ôàêòîðèçàöèè ðåøåíèÿ
ëèíåàðèçîâàííîãî óðàâíåíèÿ
Ââåäÿ òàê æå, êàê è â (1.107), îïåðàòîðû ñäâèãà
T
m
±
, ïåðåïèøåì
óðàâíåíèå (1.156) ñëåäóþùèì îáðàçîì:
(
// //
W −+−+−
−
+−
+
−+
−
+−
+
−+
CT CT C TC T
ii ii j j j j12 12 12 12
−+ =− +
−
+−
+
−++
−
ϕ−ϕ+ ϕ
CTCT VRHS
kkkk
s
snn
t
12 12
1
1
34
2
//
)D
D
y
s
,
(1.158)
74 Ãëàâà 1

ãäå
W
D
=++− −
−
+
+
−
−
+
+
−
−
15
12 12 12 12 12
,
// / / /
V
t
MV C C C
ii j j k
+C +C
+
+
−
− C
k 12/
.
Òåïåðü íåÿâíûé îïåðàòîð â ëåâîé ÷àñòè óðàâíåíèÿ (1.158) ìîæåò
áûòü ïðèáëèæåííî ôàêòîðèçîâàí:
()
WW
W
−−− ×
×+
−
+−
−
+−
−
+−−
+
−
CT C T C T
CT
ii j j kk
ii
12 12 12
1
12
///
/
()
+
+
−+
+
−+ +
−
=
=− +
ϕ−ϕ +ϕ
+C +C
jj kk
s
snn
TT
VRH
t
12 12
1
1
34
2
//
D
D
y
S
s
(1.159)
è îáðàùåí ïîñëåäîâàòåëüíî â äâà äðîáíûõ øàãà:
ïåðâûé øàã
DW
D
D
y
y
ijk
snn
s
ii
t
VRHS
C
*
/
=− + +
⎛
⎝
⎜
⎜
+
−
−
−
+
−
ϕ−ϕ+ϕ
1
1
12 1
34
2
)
jk j ij k k ij k
CC
*
/
*
/
*
;++
−
+
−−
+
−12 1 12 1
DDyy
(1.160)
âòîðîé øàã
DDW D Dyy y y
ijk
s
ijk i i jk
s
jij
C
+−
+
−
+
+
+
−
+
=−
11
12 1
1
12 1
*
//
+C
()
k
s
kijk
s+
+
−
+
+1
12 1
1
+C
/
.Dy
(1.161)
Íà ïåðâîì øàãå ïî ôîðìóëå áåãóùåãî ñ÷åòà (1.160) ñîâåðøàåòñÿ
ðàçîâûé îáõîä ðàñ÷åòíîé îáëàñòè â íàïðàâëåíèè âîçðàñòàíèÿ âñåõ èí
-
äåêñîâ è îïðåäåëÿåòñÿ âñïîìîãàòåëüíàÿ âåëè÷èíà
Dy
*
. Íà âòîðîì
øàãå òàêæå ïî ôîðìóëå áåãóùåãî ñ÷åòà (1.161), íî â íàïðàâëåíèè óáû
-
âàíèÿ âñåõ èíäåêñîâ âû÷èñëÿåòñÿ íåâÿçêà
Dy
s +1
, ïî êîòîðîé çàòåì íà
-
õîäÿòñÿ çíà÷åíèÿ íà s + 1-é èòåðàöèè n + 1-ãî ñëîÿ
ϕ=ϕ+
++ss s11
Dy
.
1.3.7. Ìåòîä ðåøåíèÿ óðàâíåíèé
äâóõñëîéíîé
k −å
ìîäåëè òóðáóëåíòíîñòè
 äâóõñëîéíîé ìîäåëè óðàâíåíèå äëÿ
k
ñîâïàäàåò ñ èñïîëüçóå
-
ìûì â äðóãèõ ðàññìîòðåííûõ
k − e
ìîäåëÿõ è ðåøàåòñÿ òàêèì æå ìå
-
òîäîì. Â óðàâíåíèè äëÿ
e
, â îòëè÷èå îò ïðèìåíÿåìîãî â äðóãèõ ìîäå
-
ëÿõ, ïîÿâëÿþòñÿ äîïîëíèòåëüíûå êîýôôèöèåíòû è èñòî÷íèêîâûå
÷ëåíû, ÷èñëåííîå ïðåäñòàâëåíèå êîòîðûõ òðåáóåò ìîäèôèêàöèè èñ
-
õîäíîãî ìåòîäà. Ðàññìîòðèì ýòîò âîïðîñ ïîäðîáíåå.
Ìåòîä ÷èñëåííîãî ðåøåíèÿ òðåõìåðíûõ çàäà÷ äèíàìèêè 75

Ïåðåïèøåì óðàâíåíèå (1.17) ñëåäóþùèì îáðàçîì:
()
11
2
1
−++ −
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
++−
⎛
∂
∂
∂
∂
∂
∂
∂
∂
llle l l
e
t
ee
ee
tx x T
j
j
j
uv C
()
⎝
⎜
⎞
⎠
⎟
=
=+−
e
ll
e
e
e
CG C
k
k
l
D1
32
1
/
,
(1.162)
ãäå
T
— òóðáóëåíòíûé ìàñøòàá âðåìåíè îïðåäåëåí â (1.150).
Âåëè÷èíà
e
âî âñåõ ÷ëåíàõ ëåâîé ÷àñòè óðàâíåíèÿ (1.162) ïðè àï
-
ïðîêñèìàöèè ýêâèâàëåíòíîãî åìó èíòåãðàëüíîãî çàêîíà ñîõðàíåíèÿ
áåðåòñÿ íåÿâíî ñ s + 1-é èòåðàöèè n + 1-ãî ñëîÿ ïî
t
. Òîãäà ïîëó÷àåòñÿ
ñõåìà âèäà
()1
111
34
2
−+
++−
−−+
ll
ee
t
eee
ijk
s
ijk
s
ijk
ijk
s
ijk
n
ijk
n
V
D
[]
Dt
V
S
ijk
mm
s
m jjk
x
+
+⋅−⋅−
−
+−
+
=
∑
le e
ln
e
() ()
//
,,
uS uS
12 12
1
∂
∂
∂
∂
∂
∂
++
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
−
⎧
⎨
⎪
⎩
⎪
−
+
=
∑
eee
xyz
SS
yz
m
mijk
12/
,,
n
l
e
eee
SSS
xyz
m
s
xyz
∂
∂
∂
∂
∂
∂
++
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
⎫
⎬
⎪
⎭
⎪
+
+
−
+
12
1
/
CVCGC
Tk
k
l
s
ij k
Dee
le l l
e
2
1
1
32
1
11+−
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
=+−
+
()
/
e
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
s
ijk
V .
(1.163)
Çäåñü ïðèíÿòû òå æå îáîçíà÷åíèÿ, ÷òî è ðàíüøå.
Àïïðîêñèìàöèÿ íåâÿçêèõ è âÿçêèõ ïîòîêîâ â (1.163) îñóùåñòâëÿ
-
åòñÿ òàê æå, êàê è â ðàçä. 1.3.3. Çàòåì ïðîâîäÿòñÿ ëèíåàðèçàöèÿ è
LU-ôàêòîðèçàöèÿ ñõåìû, ïîñëå ÷åãî îíà ïðåäñòàâëÿåòñÿ â âèäå äâóõ
äðîáíûõ øàãîâ:
DW
D
el
eee
ijk
snn
ijk
ijk
s
t
VRHS
*
=×−
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
++
⎛
−
−
−+
1
1
34
2
⎝
⎜
⎜
+++
−
+
−−
+
−−
+
−
CC C
iijkj ijkk
ijk
12 1 12 1 12
1
/
*
/
*
/
DDDee e
*
,
⎞
⎠
⎟
⎟
DDW D Dee e e
ijk
s
ikj i i jk
s
jij
CC
+−
+
+
+
+
+
+
+
=− +
11
12 1
1
12 1
*
//
()
k
s
kijk
s
C
+
+
+
+
+
+
1
12 1
1
/
De
,
76 Ãëàâà 1

ïåðâûé èç êîòîðûõ ðàçðåøàåòñÿ ðàçîâûì îáõîäîì ðàñ÷åòíîé îáëàñòè
â íàïðàâëåíèè âîçðàñòàíèÿ âñåõ èíäåêñîâ, à âòîðîé — â íàïðàâëå
-
íèè óáûâàíèÿ âñåõ èíäåêñîâ. Ïðè çàïèñè ïîñëåäíèõ âûðàæåíèé ââå
-
äåíû ñëåäóþùèå îáîçíà÷åíèÿ:
()()
RHS
ijk
sss
m
ss
m
mijk
=− ⋅ − ⋅
⎡
⎣
⎢
⎤
⎦
⎥
+
+
+
−
=
le euS uS
1
12
1
12//
,,
∑
+
+++
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
−
⎧
⎨
⎪
⎩
⎪
∂
∂
∂
∂
∂
∂
+
ln
e
eee
SSS
xyz
m
s
xyz
12/
mijk
xyz
m
s
SSS
xyz
=
−
∑
−++
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
⎫
∂
∂
∂
∂
∂
∂
,,
/
n
e
eee
12
()
⎬
⎪
⎭
⎪
+
+−
⎛
⎝
⎜
⎞
⎠
⎟
+− −
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
⎡
⎣
lele
ee
e
e
CGC C
kT
k
l
D12
32
1
1
/
⎢
⎢
⎤
⎦
⎥
⎥
ijk
s
ijk
V ,
()
C
m
m
m
V
+
±
+
+
=⋅±⋅ ±
⎛
⎝
⎜
⎞
⎠
⎟
⋅
12
12
12
05
/
/
/
,||lln
e
uS uS
SS
,
() ()
W
DD
=− + + +− + −
−
+
+
115 1
2121
lll l
t
e
VV
t
ijk ijk
ijk i i
CT V C C,/
//
////
,
2
12 12 12 12
−
−
+
+
−
−
+
+
−
+
+−+−CCCC
jjkk
Deee
sss++
=−
11
.
1.3.8. ×èñëåííàÿ ðåàëèçàöèÿ
ìåòîäà ïðèñòåíî÷íûõ ôóíêöèé
×èñëåííàÿ ðåàëèçàöèÿ ìåòîäà ïðèñòåíî÷íûõ ôóíêöèé çàêëþ÷à
-
åòñÿ â òîì, ÷òî ýìïèðè÷åñêèå çàêîíû (1.33) è (1.40) èñïîëüçóþòñÿ:
1) äëÿ âû÷èñëåíèÿ âÿçêîãî ïîòîêà ÷åðåç òâåðäóþ ñòåíêó
F
w
â
óðàâíåíèÿõ îñðåäíåííîãî äâèæåíèÿ;
2) äëÿ ðàñ÷åòà èñòî÷íèêîâûõ ÷ëåíîâ
G
è
e
â k-óðàâíåíèè â ïðè
-
ëåãàþùèõ ê òâåðäîé ñòåíêå ÿ÷åéêàõ;
3) ïðè ðàñ÷åòå çíà÷åíèÿ
e
â ïðèëåãàþùåé ê òâåðäîé ñòåíêå
ÿ÷åéêå.
Äîñòèãàåòñÿ ýòî ñëåäóþùèì îáðàçîì. Âÿçêèé ïîòîê
F
w
÷åðåç
òâåðäûå ñòåíêè ðàññ÷èòûâàåòñÿ ïî ôîðìóëå
FS
ww
=− ⋅ô ||
, (1.164)
Ìåòîä ÷èñëåííîãî ðåøåíèÿ òðåõìåðíûõ çàäà÷ äèíàìèêè 77

ãäå
||S =++SSS
xyz
222
— ïëîùàäü ãðàíè, à íàïðÿæåíèå òðåíèÿ íà
ñòåíêå íàõîäèòñÿ ïî ôîðìóëå, êîòîðàÿ îáúåäèíÿåò çàâèñèìîñòè
(1.33) è (1.40):
ô
ww
P
P
y
= n
t
q
,
,
()
nn
w
P
P
y
Ey
=⋅
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
⋅
+
+
max
kar
ln
1,
, (1.165)
ãäå
q
t
îïðåäåëåíî â (1.36).
Òðóäíîñòü ðàñ÷åòà
ô
w
ïî ôîðìóëå (1.165) ñîñòîèò â òîì, ÷òî
y
+
çàâèñèò îò
t
ww
≡ ||ô
. Äëÿ ïðåîäîëåíèÿ ýòîé òðóäíîñòè B.E. Launder è
D.B. Spalding [3] ïðåäëîæèëè âû÷èñëÿòü áåçðàçìåðíîå ðàññòîÿíèå
y
P
+
îò ñòåíêè äî óçëà
P
, âõîäÿùåå â (1.165), ïî ôîðìóëå
yy
Ck
P
P
P
+
=
m
n
14 12//
. (1.166)
Òàêèì îáðàçîì, çíàÿ ñêîðîñòü
q
t
è
k
â ïðèëåæàùåé ê ñòåíêå
ÿ÷åéêå, à òàêæå ðàññòîÿíèå
y
P
îò öåíòðà ÿ÷åéêè äî ñòåíêè, ìû
íàõîäèì íàïðÿæåíèå òðåíèÿ íà ñòåíêå
ô
w
è âÿçêèé ïîòîê
F
w
.
Èñòî÷íèêîâûé ÷ëåí äëÿ k-óðàâíåíèÿ â ïðèëåæàùåé ê ñòåíêå
ÿ÷åéêå òàêæå ðàññ÷èòûâàåòñÿ ñ èñïîëüçîâàíèåì ëîãàðèôìè÷åñêîãî
çàêîíà ñòåíêè. Èñõîäèì èç ïðåäïîëîæåíèÿ, ÷òî
G
w
q
y
=
∂
∂
t
t
.
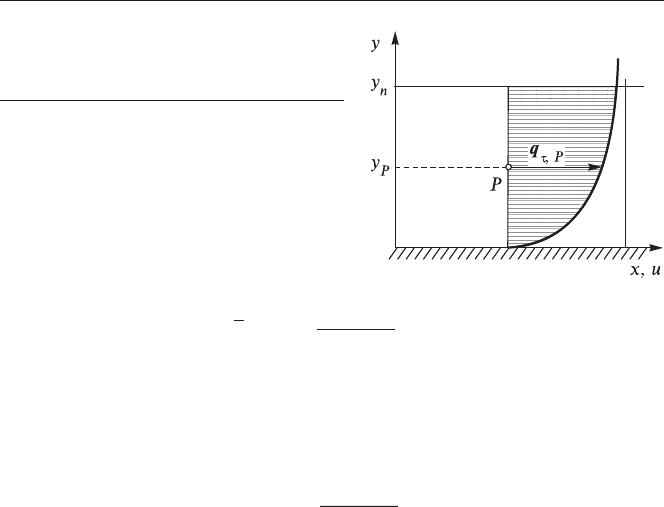
Ïîëîæèì, ÷òî ÷ëåí ãåíåðàöèè, óñðåäíåííûé ïî îáúåìó ÿ÷åéêè,
ðàâåí çíà÷åíèþ
G
â öåíòðå
P
ïðèãðàíè÷íîé ÿ÷åéêè
GGdyG
y
n
y
n
P
≡≈
∫
1
0
è òî÷êà
P
ëåæèò â ëîãàðèôìè÷åñêîì ïîäñëîå (ðèñ. 1.8).  ýòîì ñëó÷àå
G
w
P
ww
P
P
q
y
u
yCky
=
⎛
⎝
⎜
⎞
⎠
⎟
==
∂
∂
∂
∂⋅
+
+
t
t
m
t
n
t
22
14 12
kar
//
.
Âûðàæàÿ
t
w
÷åðåç
n
w
è
q
Pt,
ïî ôîðìóëå (1.165), ïîëó÷èì îêîí÷à
-
òåëüíîå âûðàæåíèå äëÿ ÷ëåíà ãåíåðàöèè òóðáóëåíòíîé ýíåðãèè
G
w
P
P
P
q
Cky
=
⋅
n
t
m
2
2
14 12 3
()
,
//
kar
.
78 Ãëàâà 1
Óñðåäíåííàÿ ïî îáúåìó ïðèãðà
-
íè÷íîé ÿ÷åéêè ñêîðîñòü äèññèïà
-
öèè
e
ïîëàãàåòñÿ ðàâíîé çíà÷åíèþ
e
â óçëå
P
, êîòîðîå âû÷èñëÿåòñÿ ñ èñ
-
ïîëüçîâàíèåì ïðåäïîëîæåíèÿ ëî
-
êàëüíîãî ðàâíîâåñèÿ
ee
m
≈=
⋅
P
P
P
Ck
y
34 32//
kar
.
Ïðè ðåøåíèè k-óðàâíåíèÿ êîíâåêòèâíûé è âÿçêèé ïîòîêè ÷åðåç
òâåðäóþ ñòåíêó ïîëàãàþòñÿ ðàâíûìè íóëþ.
 ïðèëåæàùåé ê òâåðäîé ñòåíêå (near-wall cell) ÿ÷åéêå e-óðàâíå-
íèå íå ðåøàåòñÿ, âìåñòî ýòîãî ïîëàãàåòñÿ
ee
m
=≡
⋅
nw
P
P
Ck
y
34 32//
kar
. (1.167)
Ìåòîä ÷èñëåííîãî ðåøåíèÿ òðåõìåðíûõ çàäà÷ äèíàìèêè 79
Ðèñ. 1.8. Ðàñ÷åò ãåíåðàöèè äèññèïàöèè
â ïðèãðàíè÷íîé ÿ÷åéêå.

Îñíîâíàÿ ðîëü, îòâîäèìàÿ ñðåäñòâàì ãåîìåòðè÷åñêîé ïîääåðæ
-
êè ÷èñëåííîãî ìîäåëèðîâàíèÿ òå÷åíèé, — ïîñòðîåíèå ðàñ÷åòíûõ ñå
-
òîê â èññëåäóåìûõ îáëàñòÿõ ïðîòî÷íîãî òðàêòà òóðáîìàøèíû. Ïðî
-
öåññó ãåíåðàöèè ñåòîê ïðåäøåñòâóåò îáÿçàòåëüíûé ýòàï — ãåîìåòðè
-
÷åñêîå ìîäåëèðîâàíèå ïîâåðõíîñòåé ýëåìåíòîâ ïðîòî÷íîãî òðàêòà,
îòâå÷àþùåå òðåáîâàíèÿì ìåòîäèêè ðàñ÷åòà ñåòîê. Îòìåòèì âàæíîå ñ
ýòîé òî÷êè çðåíèÿ òðåáîâàíèå.
Ïóñòü
r(, ) {(, ), (, ), (, )}xh xh xh xh= xyz
— ïàðàìåòðèçàöèÿ ïîâåðõ-
íîñòè, îïðåäåëåííàÿ â åäèíè÷íîì êâàäðàòå
01≤≤xh,
îáëàñòè ïåðå-
ìåííûõ
xh,
. Áóäåì ãîâîðèòü, ÷òî ïàðàìåòðèçàöèÿ
r(, )xh
âäîëü êîîð-
äèíàòíîé ëèíèè
hh=
*
îáëàäàåò ñâîéñòâîì êâàçèèçîìåòðè÷íîñòè,
åñëè èìååò ìåñòî ñîîòíîøåíèå
||
x
h
xh x
x
x
=
∫
1
0
s
d
()
(, )
*
*
r
,
ãäå
||
sd() (, )
**
hxhx
x
=
∫
r
0
1
.
Êàê ñëåäóåò èç ýòîãî îïðåäåëåíèÿ, ñâîéñòâî êâàçèèçîìåòðè÷íî
-
ñòè ñîñòîèò â ïðîïîðöèîíàëüíîñòè ïàðàìåòðà äëèíå äóãè êîîðäèíàò
-
íîé ëèíèè. Ïàðàìåòðèçàöèÿ êâàçèèçîìåòðè÷íà ïî ïåðåìåííîé
x
,
åñëè îíà îáëàäàåò ýòèì ñâîéñòâîì äëÿ ëþáîãî çíà÷åíèÿ ïåðåìåííîé
h
. Äëÿ ãåíåðàöèè ñåòîê ïðàêòè÷åñêèé èíòåðåñ ïðåäñòàâëÿþò ïàðà
-
ìåòðèçàöèè, êâàçèèçîìåòðè÷íûå ïî îáåèì ïåðåìåííûì
x
è
h,
ïî
-
ñêîëüêó â ýòîì ñëó÷àå ñåòêó íà ïîâåðõíîñòè ìîæíî çàäàòü ïîäõîäÿ
-
ùèìè ðàçáèåíèÿìè åäèíè÷íûõ îòðåçêîâ — îáëàñòåé èçìåíåíèÿ ýòèõ
ïåðåìåííûõ.
Èñõîäíàÿ ãåîìåòðè÷åñêàÿ èíôîðìàöèÿ îáû÷íî ïðåäñòàâëåíà â
äâóõ âèäàõ. Ýòî äàííûå êîíñòðóêòîðñêîé äîêóìåíòàöèè, çàäàþùèå
çàêîí ôîðìîîáðàçîâàíèÿ ïîâåðõíîñòè êàæäîãî ýëåìåíòà, è ãîòîâàÿ
ãåîìåòðè÷åñêàÿ ìîäåëü, ïîëó÷åííàÿ ñðåäñòâàìè êàêîé-ëèáî ñèñòåìû
ÃËÀÂÀ 2
ÃÅÎÌÅÒÐÈ×ÅÑÊÀß ÏÎÄÄÅÐÆÊÀ
×ÈÑËÅÍÍÎÃÎ ÀÍÀËÈÇÀ ÒÅ×ÅÍÈÉ
§ 2.1. ÃÅÎÌÅÒÐÈ×ÅÑÊÎÅ ÌÎÄÅËÈÐÎÂÀÍÈÅ
ÝËÅÌÅÍÒΠÏÐÎÒÎ×ÍÎÃÎ ÒÐÀÊÒÀ ÒÓÐÁÎÌÀØÈÍ
