Черняк О.І. та ін. Економетрика
Подождите немного. Документ загружается.

267
остання суттєво спирається на припущення про некорельованість
i
з
it
x
. Якщо це не
так, то слід користуватись моделлю з фіксованими ефектами. Нульову гіпотезу, що
it
x
та
i
некорельовані, можна перевірити за допомогою критерію Гаусмана, що має таку
статистику:
1
T
ˆˆ ˆ ˆ ˆˆ
ˆˆ
()
DD
()
HFERE FE RE FERE
ββ β β ββ.
Якщо нульову гіпотезу буде прийнято, то це означає, що статистика Гаусмана має
асимптотичний розділ
2
з k степенями свободи, де k – кількість параметрів у векторі
β . Під час застосування цього критерію можуть виникати обчислювальні проблеми,
оскільки матриця
ˆˆ
ˆˆ
DD
FE RE
ββ може не бути додатно визначеною за невеликих
розмірах вибірки. Псевдо-коефіцієнт детермінації розраховують як квадрат коефіцієнта
кореляції між
ˆ
it
y та .
it
y
Задачі
Група А
Задача 11.1. Модель регресії з біномиальною залежною змінною можна записати у
такому вигляді: (залежна змінна) = (математичне сподівання) + (похибка). Які припущення
класичної лінійної регресії при цьому буде порушено?
Задача 11.2. Оцінювання логіт-моделі
(
1
)
()
P
y
Fx дало результат
* -5,89 0,2 .
y
x Чому дорівнює ймовірність
1y при
50x ?
Задача 11.3. Оцінювання логіт-моделі
(
1
)
()
P
y
Fx дало результат
*-2,850,092
y
x . Чому дорівнює ймовірність
1y при
50x
?
Задача 11.4. Оцінювання пробіт-моделі
(
1
)
()
P
y
Fx дало результат
*-5,890,2
y
x . Чому дорівнює збільшення ймовірності
1y при збільшенні x на
одиницю, якщо 50x ?
Задача 11.5. Оцінювання пробіт-моделі
(
1
)
()
P
y
Fx дало результат
*-2,850,092
y
x . Чому дорівнює збільшення ймовірності
1y при збільшенні x на
одиницю, якщо 50x ?
Задача 11.6. Логіт-модель застосували до вибірки, у якій
1y , якщо продуктивність
праці на підприємстві зросла, і
0y – у протилежному випадку.
1
x
– дохід
підприємства в мільйонах гривень на рік,
1
1
G
x , якщо підприємство належить до
галузі високих технологій (
1
0
G
x у протилежному випадку). Одержано таку модель:
11
*0,50,1 0,4
G
yxx
. Знайдіть оцінку ймовірності зростання продуктивності праці для
високотехнологічного підприємства з доходом 100 млн грн на рік, а також для
підприємства, що не належить до галузі високих технологій, з доходом 150 млн грн у рік.
Задача 11.7. Маємо вибірку з 600 спостережень, у якій 1y , якщо робітник є
членом профспілки, та 0y – у протилежному випадку. Уважатимемо, що членство в
профспілці залежить від освіти (
1
x років навчання), стажу роботи (
2
x років) та статі
(
3
1x для чоловіків). Вибіркові середні становлять
0,2y ,
1
14x ,
2
18x та
3
0, 45x . На основі вибіркових даних одержано таку пробіт-модель:
12 3
* 0, 9 0, 01 0, 4 0, 62
y
xx x. Визначте, наскільки зменшується ймовірність бути
членом профспілки з розрахунку на рік додаткової освіти.
268
Група В
Задача 11.8. У табл. 11.1 наведено дані про голосування стосовно збільшення податків
на утримання шкіл у м. Троя, штат Мічиган, США у 1973 р. Досліджено результати
голосування та різні характеристики 95-ти осіб.
Pub = 1, якщо щонайменше одна дитина відвідує державну школу, в іншому разі Pub = 0;
Priv = 1, якщо щонайменше одна дитина відвідує приватну школу, в іншому разі Priv = 0;
Years = строк проживання в цьому районі; Teach = 1, якщо вчителює, в іншому разі
Teach = 0; Lnlnc = логарифм річного доходу сім'ї в доларах; РгорТах = логарифм податків
на майно в доларах за рік (замінює плату за навчання – зарплата залежить від майнового
стану); Yes = 1, якщо особа проголосувала на референдумі "за", Yes = 0 – якщо "проти".
Залежна змінна – Yes. У модель уводять усі наведені фактори, а також квадрат Years.
1. Оцініть пробіт- і логіт-моделі.
2. Обчисліть коефіцієнти логіта через коефіцієнти пробіта та порівняйте.
3. Для логіта знайдіть граничні ефекти (на ймовірність) для Teach, Lnlnc і РгорТах за
середнього рівня факторів.
4. Побудуйте графік імовірності голосування "за" залежно від Years за середнього рівня
решти факторів.
Таблиця 11.1
Номер Pu
b
Priv Year
s
Teach
Lnlnc
PropTa
x
Ye
s
1 1 0 10
1
9,77
7,0475
1
2 1 0 8
0
10,021
7,0475
0
3 1 0 4
0
10,021
7,0475
0
4 1 0 13
0
9,4335
6,3969
0
5 1 0 3
1
10,021
7,2792
1
6 1 0 5
0
10,463
7,0475
0
7 0 0 4
0
10,021
7,0475
0
8 1 0 5
0
10,021
7,2793
1
9 1 0 10
0
10,222
7,0475
0
10 1 0 5
0
9,4335
7,0475
1
11 1 0 3
0
10,021
7,0475
1
12 1 0 30
0
9,77
6,3969
0
13 1 0 1
0
9,77
6,7452
1
14 1 0 3
0
10,021
7,0475
1
15 1 0 3
0
10,82
6,7452
1
16 1 0 42
0
9,77
6,7452
1
17 1 0 5
1
10,222
7,0475
1
18 1 0 10
0
10,021
7,0475
0
19 1 0 4
0
10,222
7,0475
1
20 1 1 4
0
10,222
6,7452
1
21 1 0 11
1
10,463
7,0475
1
22 0 0 5
0
10,222
7,0475
1
23 1 0 35
0
9,77
6,7452
1
24 1 0 3
0
10,463
7,2793
1
25 1 0 16
0
10,021
6,7452
1
26 0 1 7
0
10,463
7,0475
0
27 1 0 5
1
9,77
6,7452
1
28 1 0 11
0
9,77
7,0475
0
29 1 0 3
0
9,77
6,7452
0
30 1 1 2
0
10,222
7,0475
1
269
31 1 0 2
0
10,021
6,7452
1
32 1 0 2
0
9,4335
6,7452
0
33 1 0 2
1
8,294
7,0475
0
34 0 1 4
0
10,463
7,0475
1
35 1 0 2
0
10,021
7,0475
1
36 1 0 3
0
10,222
7,2793
0
37 1 0 3
0
10,222
7,0475
1
38 1 0 2
0
10,222
7,4955
1
39 1 0 10
0
10,021
7,0475
0
40 1 0 2
0
10,222
7,0475
1
41 1 0 2
0
10,021
7,0475
0
42 1 0 3
0
10,82
7,4955
0
43 1 0 3
0
10,021
7,0475
1
44 1 0 3
0
10,021
7,0475
1
45 1 0 6
0
10,021
6,7452
1
46 1 0 2
0
10,021
7,0475
1
47 1 0 26
0
9,77
6,7452
0
48 0 1 18
0
10,222
7,4955
0
49 0 0 4
0
9,77
6,7452
0
50 0 0 6
0
10,021
7,0475
0
51 0 0 12
0
10,021
6,7452
1
52 1 0 49
0
9,4335
6,7452
1
53 1 0 6
0
10,463
7,2793
1
54 0 1 18
0
9,77
7,0475
0
55 1 0 5
0
10,021
7,0475
1
56 1 0 6
0
9,77
5,9915
1
57 1 0 20
0
9,4335
7,0475
0
58 1 0 1
1
9,77
6,3969
1
59 1 0 3
0
10,021
6,7452
1
60 1 0 5
0
10,463
7,0475
0
61 1 0 2
0
10,021
7,0475
1
62 1 1 5
0
10,82
7,2793
0
63 1 0 18
0
9,4335
6,7452
0
64 1 0 20
1
9,77
5,9915
1
65 0 0 14
0
8,9227
6,3969
0
66 1 0 3
0
9,4335
7,4955
0
67 1 0 17
0
9,4335
6,7452
0
68 1 0 20
0
10,021
7,0475
0
69 1 1 3
0
10,021
7,0475
1
70 1 0 2
0
10,021
7,0475
1
71 0 0 5
0
10,222
7,0475
1
72 1 0 35
0
9,77
7,0475
1
73 1 0 10
0
10,021
7,2793
0
74 1 0 8
0
9,77
7,0475
1
75 1 0 12
0
9,77
7,0475
0
76 1 0 7
0
10,222
6,7452
1
77 1 0 3
0
10,463
6,7452
1
78 1 0 25
0
10,222
6,7452
0
270
79 1 0 5
1
9,77
6,7452
1
80 1 0 4
0
10,222
7,0475
1
81 1 0 2
0
10,021
7,2793
1
82 1 0 5
0
10,463
6,7452
1
83 1 0 3
0
9,77
7,0475
0
84 1 0 2
0
10,82
7,4955
1
85 0 1 6
0
8,9227
5,9915
0
86 1 1 3
0
9,77
7,0475
1
87 1 0 12
0
9,4335
6,3969
1
88 0 0 3
0
9,77
6,7452
1
89 1 0 3
0
10,021
7,0475
1
90 0 0 3
0
10,021
6,7452
1
91 1 0 3
0
10,222
7,2793
1
92 1 0 3
1
10,021
7,0475
1
93 1 0 5
0
10,021
7,0475
1
94 0 0 35
1
8,9277
5,9915
1
95 1 0 3
0
10,463
7,4955
0
Джерело: R. Pindyck and D. Rubinfeld, Econometric Models and Economic Forecasts, 1998,
Fourth Edition, Table 11.8, p. 332
Задача 11.9. Далі подано панельні дані щодо інвестицій (y) і прибутків (x) для
3n
фірм протягом 10T періодів.
i
= 1
i
= 2
i
= 3
t y x y x y x
1 13
32
12
85
20
30
22
93
8,
85
8,
65
2 26
30
25
69
17
47
17
96
19
60
16
55
3 2,
62
5,
48
9,
31
9,
16
3,
87
1,
47
4 14
94
13
79
18
01
18
73
24
19
24
91
5 15
80
15
41
7,
63
11
31
3,
99
5,
01
6 12
20
12
59
19
84
21
15
5,
73
8,
34
7 14
93
16
64
13
76
16
13
26
68
22
70
8 29
82
26
45
10
00
11
61
11
49
8,
3
6
9 20
32
19
64
19
51
19
55
18
49
15
44
1
0
4,
77
5,
43
18
32
17
06
20
84
17
87
1. Об'єднайте дані й обчисліть коефіцієнти МНК-регресії для моделі
T
it it it
y x β .
Оцініть модель із фіксованими ефектами і перевірте гіпотезу про те, що доданок
постійний для всіх фірм.
2. Оцініть модель із випадковими ефектами і перевірте гіпотезу про можливість
застосування класичної моделі без урахування спільних ефектів.
3.
За допомогою критерію специфікації Гаусмана порівняйте моделі з випадковими і
фіксованими ефектами.
317
ЧАСТИНА 3. ВИКОРИСТАННЯ СТАТИСТИЧНИХ ПАКЕТІВ
ДЛЯ РОЗВ’ЯЗАННЯ ЕКОНОМЕТРИЧНИХ ЗАДАЧ
Верстальнику: назви програм – Arial курсив; опції
програм – Arial прямо
Розділ 12. Розв'язання задач у середовищі MS Excel
12.1. Налаштування MS Excel
Для побудування економетричних моделей Excel пропонує
обмежені можливості, дозволяючи використовувати лише звичайний
метод найменших квадратів. Проте для більшої частини прикладних
розрахунків цього буває достатньо.
Варто зазначити, що Excel пропонує широкі можливості для
здійснювання власних розрахунків та оцінювання регресій. Проте на
практиці цим користуються рідко, адже набагато зручніше
використовувати готові статистичні програми.
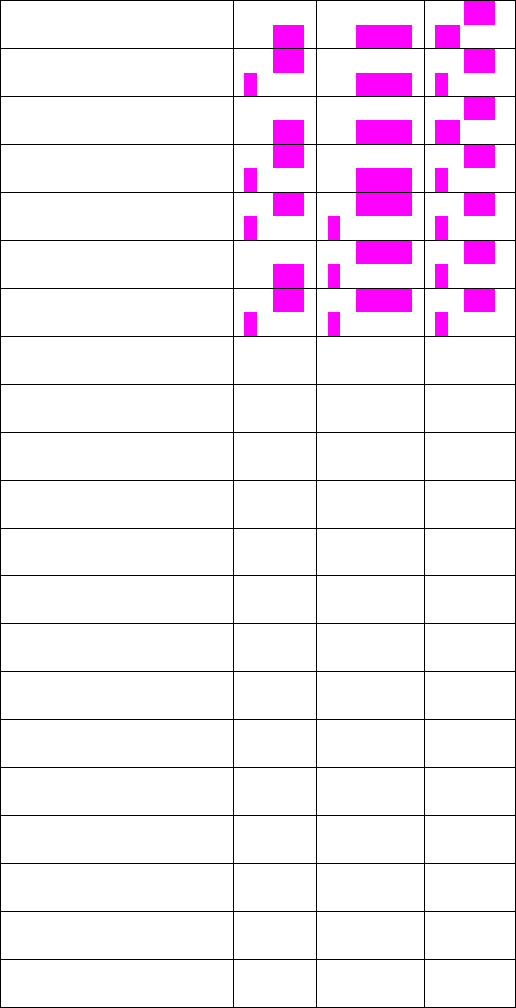
Для оцінювання регресійних моделей в MS Excel треба перевірити
наявність пакету аналізу. Для цього в головному меню слід обрати
СервисНадстройки і ввімкнути пакет аналізу:
Рис.12.1. СервісНадстройки

318
Якщо відповідний пакет відсутній у вікні, то слід змінити
установки MS Office, додавши відповідний компонент.
Безпосереднє оцінювання регресії в Excel можна здійснити за
допомогою команди СервисАнализ данныхРегресия (якщо
використовується MS Excel до версії 2003 року) або команди
ДанныеАнализ данных (якщо використовується MS Excel 2007).
Приклад 12.1. Розв’язання задачі в MS Excel
Для поданих значень змінних побудувати регресію залежності
державних видатків на освіту (ЕЕ) від валового внутрішнього
продукту (GDP) і кількості населення (РР) такого виду:
01122
.
tt
YXX
Таблиця 12.1
(???)
Країна
EE
(Y)
GDP
(X
1
)
PP
(X
2
)
Люксембург
0,3
4 5,67
0,3
6
Уругвай
0,2
2 10,13 2,9
Сінгапур
0,3
2 11,34
2,3
9
Ірландія
1,2
3 18,88
3,4
4
Ізраїль
1,8
1 20,94
3,8
7
Угорщина
1,0
2 22,16
10,
71
Нова Зеландія
1,2
7 23,83 3,1
Португалія
1,0
7 24,67
9,9
3
Гонконг
0,6
7 27,56
5,0
7
Чилі
1,2
5 27,57
11,
1
Греція
0,7
5 40,15 9,6
Фінляндія 2,8 51,62
4,7
8
Норвегія 4,9 57,71
4,0
9
319
Сербія й
Чорногорія
3,5 63,03
22,
34
Данія
4,4
5 66,32
5,1
2
Туреччина 1,6 66,97
44,
92
Австрія
4,2
6 76,88
7,5
1
Швейцарія
5,3
1
101,6
5
6,3
7
Саудівська
Аравія
6,4
115,9
7
8,3
7
Бельгія
7,1
5
119,4
9
9,8
6
Швеція
11.
22
124.1
5
8.3
1
Австралія
8.6
6
140.9
8
14.
62
Аргентина
5.5
6
153.8
5
27.
06
Нідерланди
13.
41
169.3
8
14.
14
Мексика
5.4
6
186.3
3
67.
4
Іспанія
4.7
9
211.7
8
37.
43
Бразилія
8.9
2
249.7
2
123
.03
Канада
18.
9
261.4
1
23.
94
Італія
15.
95
395.5
2
57.
04
Велика Британія
29.
9
534.9
7
55.
95
Франція
33.
59
655.2
9
53.
71
Німеччина
38.
62 815
61.
56
Японія
61.
61
1040.
45
116
.78
США
18
1.3
2586.
4
227
.64
Перевірити модель на адекватність та коефіцієнти на значущість,
0,05.
Розв'язання
320
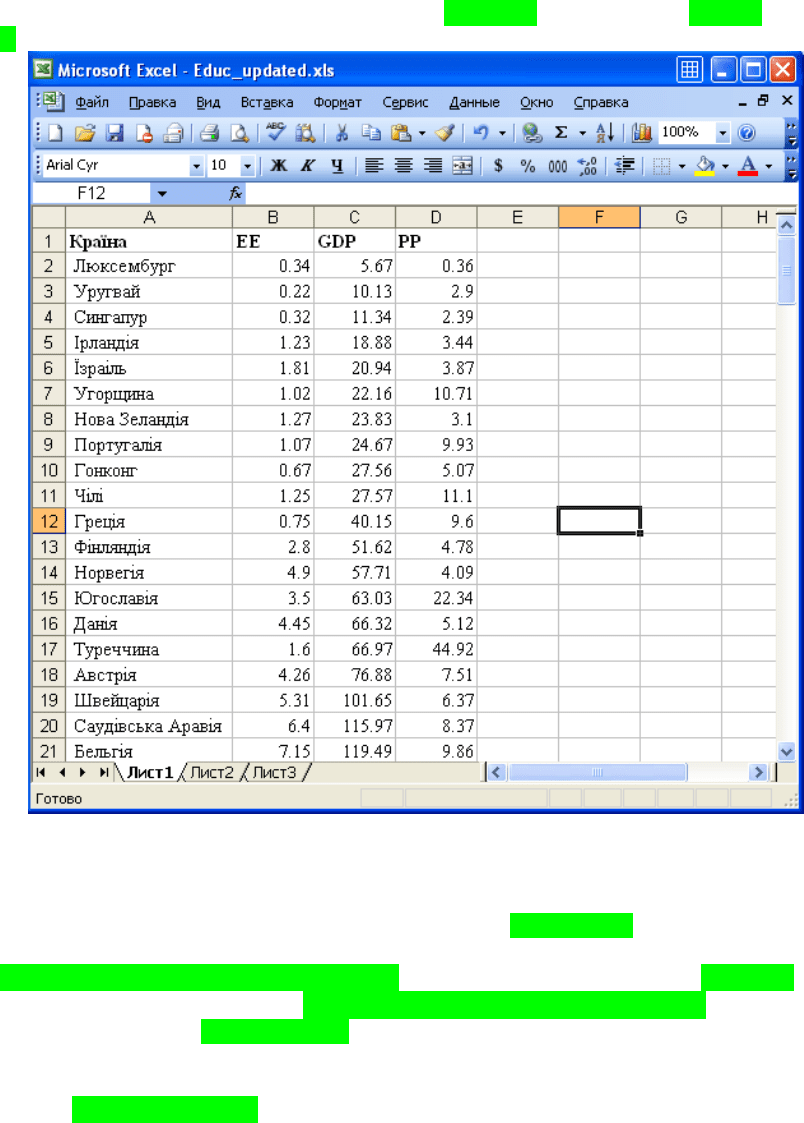
Спочатку введемо початкові дані до MS Excel у стовпчики A, B, C та
D:
Рис.12.2. Початкові дані
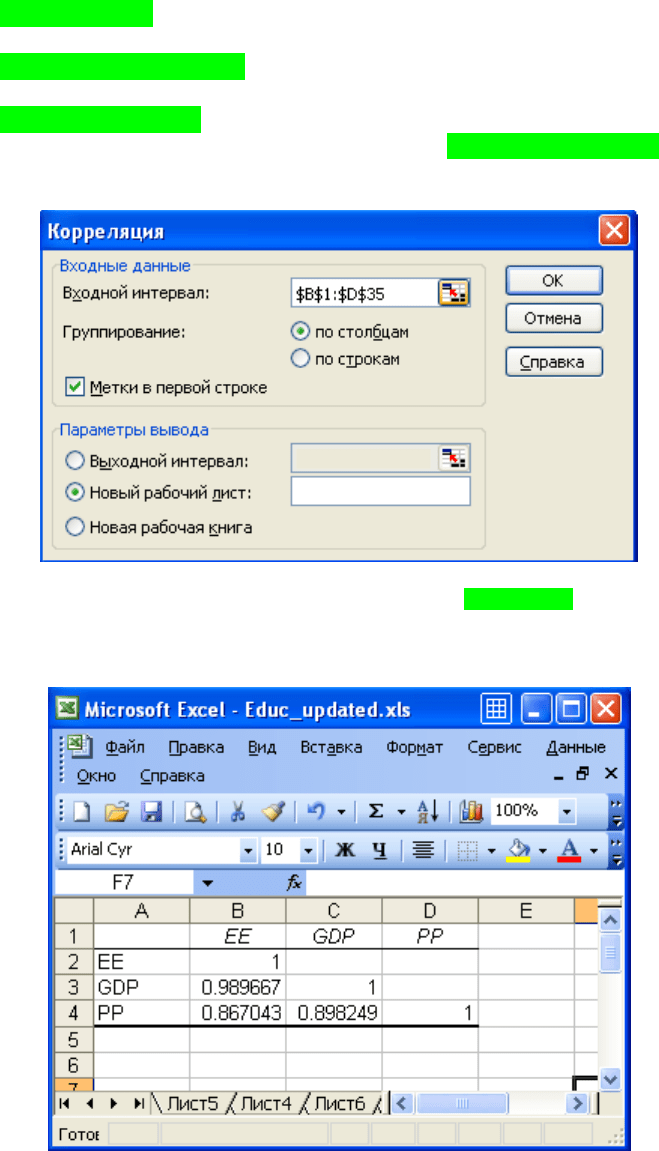
Матрицю парних коефіцієнтів кореляції можна розрахувати,
використовуючи інструмент аналізу даних Корреляция. Для цього в
головному меню слід обрати команди:
СервисАнализ данныхКорреляция (якщо використовують MS Excel
до версії 2003 р.) або ДанныеАнализ данныхКорреляция (якщо
використовують MS Excel 2007) і заповнити діалогове вікно вводу
даних та параметрів вводу.
Серед основних опцій діалогового вікна слід зазначити такі:
входной интервал – діапазон значень змінних;
321
группирование – опція, що вказує на розташування значень
змінних;
метки в первой строке – опція, що вказує, чи містить перший
рядок назви стовпчиків;
параметры вывода – адреса верхньої лівої чарунки для виводу
результатів обчислень (якщо вказано опцію Новый рабочий лист, тоді
результати виводяться на новий лист).
Рис.12.3. Інструмент аналізу даних Корреляция
Отримані результати розрахунків матриці парних коефіцієнтів
кореляції:
322
Рис.12.4. Матриця парних коефіцієнтів кореляції
Отримані результати коефіцієнтів кореляції між змінними досить
великі, що дозволяє побудувати задану регресійну модель.
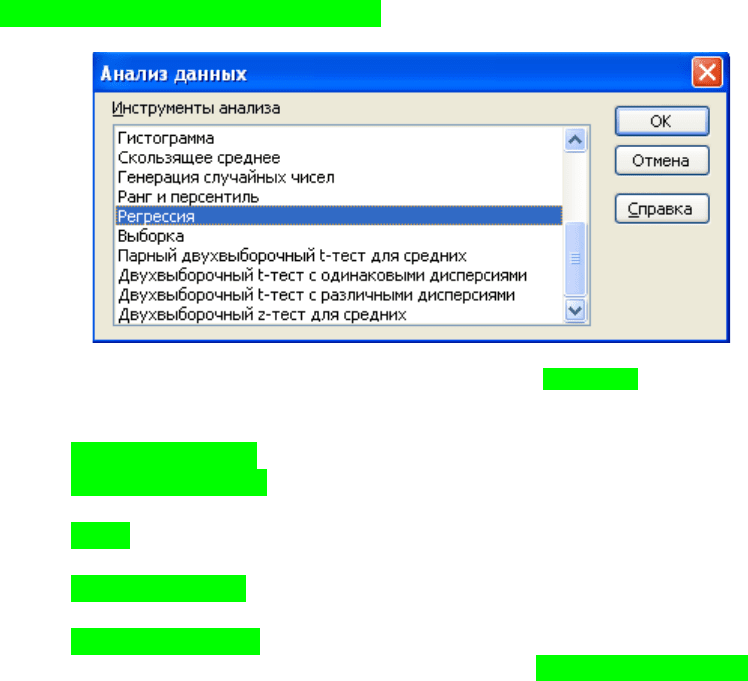
Для цього в головному меню вибираємо
СервисАнализ данныхРегрессия:
Рис.12.5. Інструмент аналізу даних Регрессия
Серед основних опцій діалогового вікна слід зазначити такі:
входной интервал y – діапазон значень залежної змінної;
входной интервал x – діапазон значень незалежних змінних
(зауважте, що незалежні змінні мають бути в сусідніх стовпчиках);
метки – опція, що вказує, чи містить перший рядок назви
стовпчиків;
константа – ноль – опція, що вказує на наявність чи відсутність
константи в регресії;
параметры вывода – адреса верхньої лівої чарунки для виводу
результатів обчислень (якщо вказано опцію Новый рабочий лист, то
результати виводяться на новий лист).
Якщо треба додатково отримати залишки, то слід позначити
відповідні опції в діалоговому вікні.
Отже, заповнюємо діалогове вікно згідно з параметрами задачі:
