Черняк О.І. та ін. Економетрика
Подождите немного. Документ загружается.


11
залежати від їхніх доходів і рівня цін. Виходячи із цієї теоретичної залежності,
економетрист може побудувати таку залежність:
01 2
ln ln ln
tttt
CYP
, 1,tn ,
де
t
C – споживання деякого продукту на душу населення у період t ;
t
Y – реальний дохід
на душу населення в цьому самому періоді;
t
P – індекс цін на цей продукт, скоригований
на інфляцію;
,0,1,2
t
t – коефіцієнти моделі;
t
– випадкова величина; n – кількість
наявних спостережень.
Отримане рівняння описує поведінку споживача залежно від відносного рівня цін на
продукт і реального доходу. Закон поведінки буде остаточно визначено, щойно ми
знайдемо значення коефіцієнтів моделі.
Таким чином, перше завдання економетриста – оцінити ці коефіцієнти.
Друге завдання, що стоїть перед економетристом – обґрунтувати можливість
використовувати одержане
рівняння у практичній діяльності. Для цього слід перевірити
адекватність моделі, значущість її коефіцієнтів, їхню стійкість, відповідність збурень
моделі до всіх необхідних статистичних властивостей, правильність обраної
функціональної форми моделі тощо. Таким чином, економетричні методи дозволяють не
лише визначати кількісні зв'язки між економічними змінними, але й робити висновки про
статистичну коректність одержаних
моделей. У (статистично) коректній моделі можна
формулювати положення економічної теорії у вигляді статистичних гіпотез.
Третє завдання – це здійснення всебічного аналізу моделі. Слід визначити, як саме
фактори впливають на рівень споживання, що відбудеться, якщо значення факторів
збільшиться на певну величину. Також доцільно зробити прогноз споживання на
майбутнє.
Економетричне моделювання широко застосовують
як в економічних дослідженнях,
так і в роботі аналітичних підрозділів державних установ і фірм. За розроблення
економетричного апарату регулярно присуджують Нобелівські премії в галузі економіки.
12
ЧАСТИНА 1. КЛАСИЧНА ЕКОНОМЕТРИКА
Розділ 1. Проста лінійна регресія
1.1. Описання моделі
Припустимо, що існують дві змінні x i y , де x – незалежна змінна (регресор), y –
залежна змінна. Співвідношення між цими змінними позначимо
()
yf
x . При
статистичному співвідношенні кожному значенню x відповідає не єдине значення
y
, але
залежну змінну
y
можливо точно описати в імовірнісних термінах. Припустимо, що
функція
()
f
x лінійна за
x
, тобто ()
f
xx
, а співвідношення між
x
та
y
–
статистичне, а саме
yx
, (1.1)
де доданок
називається збуренням, або похибкою, або випадковим членом регресії і
має відомий імовірнісний розподіл (тобто є випадковою величиною). У рівнянні (1.1)
x
є детермінованим компонентом, збурення
– випадковий, або стохастичний
компонент;
і називаються регресійними коефіцієнтами, або параметрами регресії,
які треба оцінити на основі даних про
x та
y
.
Нехай існує n пар значень
(
,
)
,1,
tt
x
y
tn , які називаються спостереженням. Рівняння
(1.1) можна записати тоді у вигляді
.
ttt
yx
(1.2)
Оцінити регресію (1.1) означає знайти оцінки коефіцієнтів
ˆ
та
ˆ
. Це можна зробити,
наприклад, за допомогою методу найменших квадратів (МНК), суть якого буде розглянуто
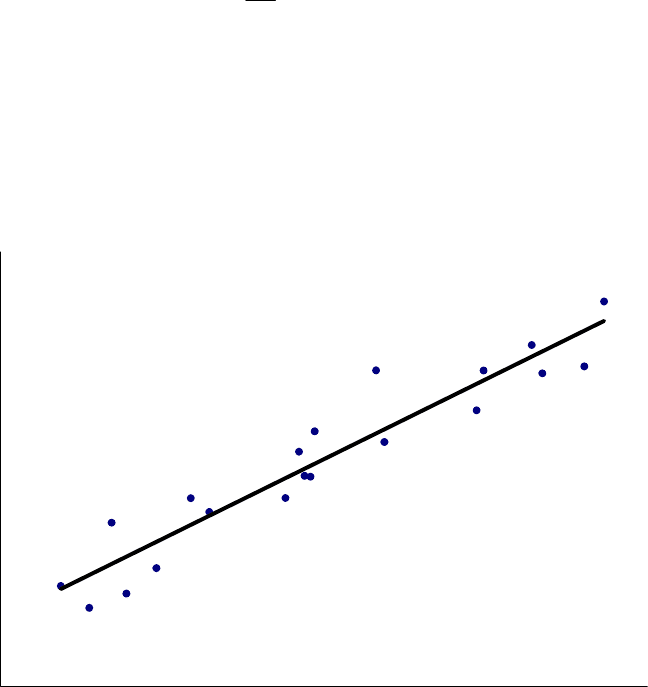
в підрозд. 1.2. Оцінивши регресію, отримаємо певну лінію регресії, яка проходитиме
крізь точки спостережень, як показано на рис. 1.1.
x
y
ˆ
ˆ
yx
Рис. 1.1. Лінія регресії та спостереження
Метою регресійного аналізу є знайти найкращі оцінки невідомих коефіцієнтів
і
у
рівнянні (1.2) на основі n спостережень
x
та
y
. Безумовно, оцінки можна вважати
вдалими, якщо лінія регресії проходитиме відносно недалеко від реальних спостережень.
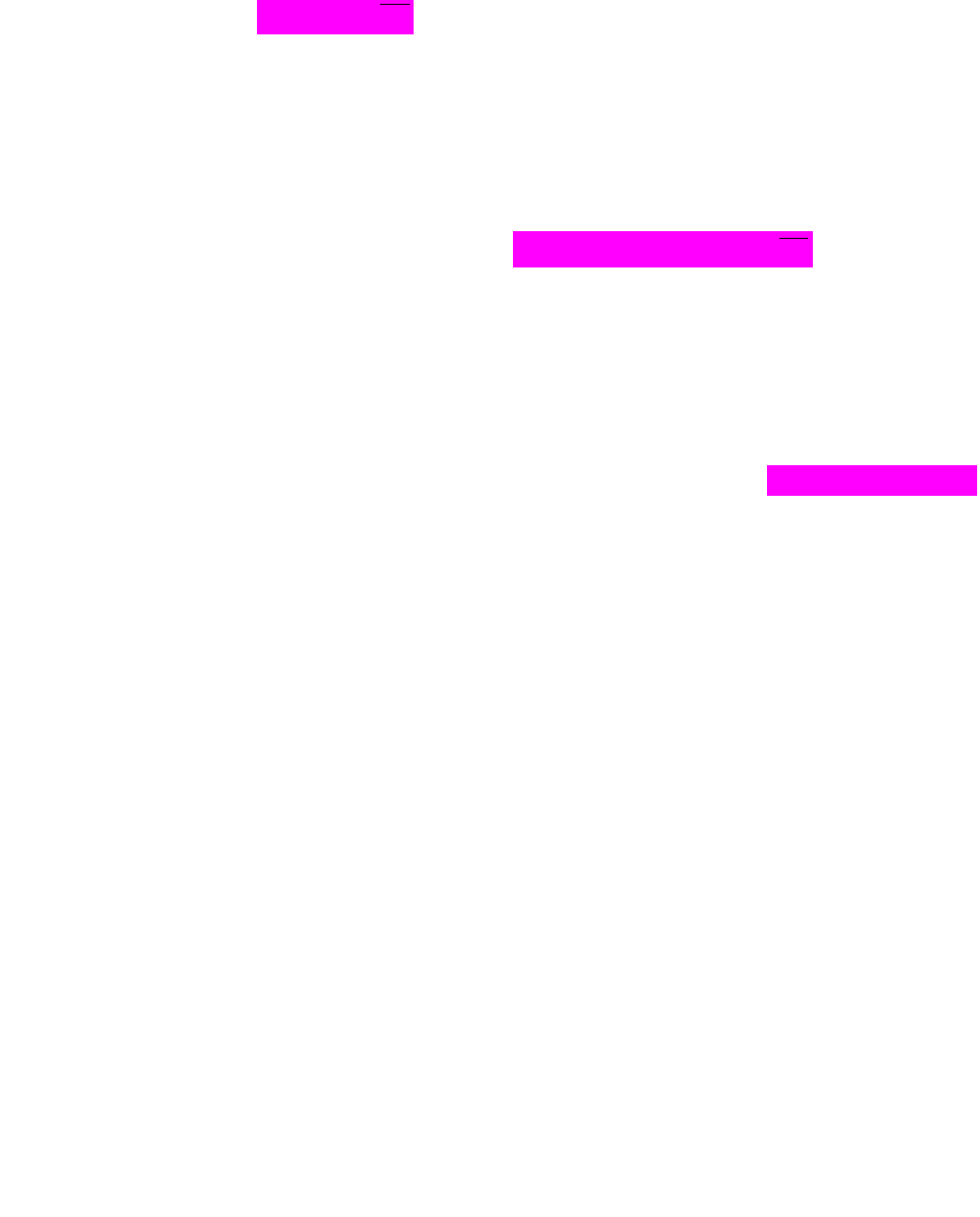
13
Різниці між фактичними значеннями та регресійною оцінкою залежної змінної
називатимемо залишками.
Щоб отримати можливість здійснити статистичний аналіз моделі, про який ішлося в
передмові, треба висунути деякі умови щодо збурень
t
:
1. Нульове середнє M0, 1,
t
tn.
Перша умова полягає в тому, що математичне сподівання збурень у будь-якому
спостереженні має дорівнювати нулю. Іноді випадковий член буде позитивним, іноді
негативним, але він не має систематично зсуватися в жодному із двох можливих
напрямків.
Фактично якщо рівняння регресії містить постійний член, то зазвичай можна
припустити, що ця умова виконується автоматично, тому що роль константи полягає у
визначенні будь-якої систематичної тенденції в у, що не враховують пояснювальні змінні,
уведені в рівняння регресії.
2. Рівність дисперсій (гомоскедастичність)
22
DM const,1,
ti
tn.
Друга умова полягає в тому, що дисперсія збурень має бути постійною для всіх
спостережень. Іноді випадковий член буде більшим, іноді меншим, однак, не має бути
апріорної причини для того, щоб він породжував більшу помилку в одних
спостереженнях, ніж в інших. Величина дисперсії, звичайно, невідома. Отже, одне із
завдань регресійного аналізу
– оцінити стандартне відхилення випадкового члена.
Якщо розглянута умова не виконується, то коефіцієнти регресії, знайдені за звичайним
методом найменших квадратів (див. підрозд. 1.2), будуть неефективні, а тому можна
одержати надійніші результати шляхом застосування модифікованого методу регресії.
3. Незалежність збурень:
t
та
незалежні при t
. Зокрема,
cov( , ) M 0
tt
при t
.
Ця умова припускає, що не має систематичного зв'язку між значеннями випадкового
члена в будь-яких двох спостереженнях. Наприклад, якщо випадковий член великий і
позитивний в одному спостереженні, це не може зумовлювати систематичну тенденцію
до того, що він буде більшим і позитивним у наступному спостереженні (або більшим і
негативним, або
малим і позитивним, або малим і негативним). Випадкові члени мають
бути абсолютно незалежними один від одного. Якщо цю умову не буде виконано, то
регресія, оцінена за звичайним методом найменших квадратів, знову дасть неефективні
результати.
4. Незалежність збурень і регресора: вектори
x
та
незалежні для всіх періодів
часу. Це припущення вводять для того, щоб значення будь-якої незалежної змінної в
кожному спостереженні вважати екзогенним, тобто цілком зумовленим зовнішніми
причинами, урахованими не в рівнянні регресії. Якщо таке припущення не виконується,
то оцінки регресії за звичайним методом найменших квадратів будуть зміщеними.
5. Нормальність збурень. Збурення
t
нормально розподілені для всіх t :
2
~(0, )
t
N.
Узявши до уваги припущення 1–3, можна сказати, що
t
– незалежні нормально
розподілені випадкові величини з нульовим математичним сподіванням і однаковими
дисперсіями
2
, або
2
~(0, )
t
N. Якщо випадковий член має нормальний розподіл, то
такими самими будуть і розподіли коефіцієнтів регресії. Ця умова необхідна, щоб
перевірити гіпотези і визначити надійні інтервали для параметрів, використовуючи
результати оцінювання регресії.
Припущення про нормальність ґрунтується на центральній граничній теоремі. По суті,
теорема стверджує, що якщо випадкова величина є загальним результатом взаємодії
великої кількості інших випадкових величин, жодна з яких не є домінуючою, то вона
матиме приблизно нормальний розподіл, навіть якщо окремі складники не мають
нормального розподілу. У розд. 3 ми розглянемо властивість асимптотичної нормальності,
яка дозволяє розповсюдити стандартні процедури перевірки гіпотез на більш широкий
клас моделей.
Отже, модель простої лінійної регресії описують за допомогою рівнянь (2), а збурення
цієї моделі задовольняють припущенням 1–5.
14
1.2. Знаходження оцінок параметрів регресії методом найменших квадратів
Нехай
ˆ
і
ˆ
– деякі оцінки параметрів
та
. Запишемо рівняння вибіркової регресії
ˆ
ˆ
ˆ
y
x
.
Тоді оцінкою математичного сподівання величини залежної змінної
t
y , побудованою на
основі вибіркової регресії буде
ˆ
ˆ
ˆ
tt
y
x
.
Позначимо через
ˆ
ˆ
iii
yy різницю між значенням y, яке спостерігалось, і обчисленим
з регресії. Оцінки методу найменших квадратів (скорочено – МНК-оцінки) знаходять з
умови мінімізації за всіма можливими значеннями
ˆ
та
ˆ
виразу
22
11
ˆ
ˆˆ
()
.
nn
ii i
ii
Qyx
(1.3)
Якщо позначити на координатній площині координати точок
(
,
)
,1,
tt
x
y
tn і побудувати
графік прямої
ˆ
ˆ
ˆ
y
x , то можна сказати, що треба знайти пряму, яка буде
найближчою до цих точок (у тому розумінні, що сума квадратів відстаней по вертикалі
від цих точок до прямої буде найменшою), як показано на рис. 1.2.
x
y
ˆ
ˆ
yx
ˆ
i
Рис. 1.2. Залишки моделі
Якщо просто мінімізувати суму залишків, то вона автоматично буде рівною нулю при
y
та 0 , тобто найкращою регресійною лінією буде пряма ó
y
. У цьому разі
додатні залишки буде врівноважено від'ємними. Проте така лінія не покаже впливу однієї
змінної на іншу, а тому вона не має сенсу. Для розв'язання проблеми слід
використовувати мінімізацію квадратів відхилень, що фактично накладає штраф за будь-
яке відхилення від справжніх значень незалежно від знаку такої помилки
.
Щоб мінімізувати вираз (1.3), запишемо необхідну умову екстремуму, тобто
прирівняємо похідні стосовно
ˆ
та
ˆ
до нуля. Маємо
1
ˆ
ˆ
2
()(
1
)
0
ˆ
n
tt
t
Q
yx
,
звідки
11
ˆ
ˆ
,
nn
tt
tt
yn x
(1.4)
і
1
ˆ
ˆ
2
()()
0
ˆ
n
ttt
t
Q
yxx
,
звідки
2
111
ˆ
ˆ
.
nnn
tt t t
ttt
yx x x
(1.5)

15
Система рівнянь (1.4) і (1.5) називається системою нормальних рівнянь.
Уведемо такі позначення:
1
n
t
t
x
x
n
;
1
n
t
t
y
y
n
;
222
11
()
nn
xx t t
tt
Sxxxnx
;
222
11
()
nn
yy t t
tt
S
yy y
n
y
;
11
()()
nn
xy t t t t
tt
Sxx
yy
x
y
nx
y
.
Нехай 0
xx
S . Запишемо розв'язок системи нормальних рівнянь стосовно
ˆ
за
правилом Крамера:
111
22
11
ˆ
.
()
nnn
tt t t
ttt
nn
tt
tt
nx
y
x
y
nx x
(1.6)
Розділимо чисельник і знаменник виразу (1.6) на
n. Ураховуючи введені позначення,
остаточно одержимо
ˆ
xy
xx
S
S
.
Значення коефіцієнта
ˆ
можна також знайти за правилом Крамера, проте, набагато
легше знайти його за іншою методикою. Розділимо перше нормальне рівняння (1.4)
почленно на n. Маємо
ˆ
ˆ
y
x
.
Отже, МНК-оцінки параметрів моделі простої лінійної регресії можна знайти за
формулами
ˆ
,
ˆ
.
xy
xx
S
S
y
bx
(1.7)
Якщо обчислити матрицю других похідних для Q , то можна побачити, що ця матриця
додатно
визначена, отже, значення (1.7) насправді мінімізують (1.3).
Рівняння вибіркової регресії набуває вигляду
ˆ
ˆ
ˆ
y
x
. (1.8)
З першого нормального рівняння випливає, що
графік вибіркової регресійної прямої
(1.8) проходить через точку середніх значень залежної та незалежної змінних.
Рівняння (1.8) дає уявлення про характер залежності (точніше, детермінованої її частини)
між змінними
x
та
y
.
Серед переваг методу найменших квадратів слід виокремити передусім надзвичайну
простоту математичного дослідження й отримання результатів. Очевидно, що за
допомогою комп'ютерної техніки отримання оцінок регресії зводиться лише до технічної
роботи. Крім цього, отримані оцінки мають достатні статистичні властивості для
перевірки статистичних гіпотез. Недоліком методу є сильна залежність отриманих
результатів від
великих збурень і коливань. У подальших розділах буде розглянуто
ситуації, у яких для оцінювання регресії доведеться замість методу найменших квадратів
використовувати інші підходи (див. розд. 4, 5).

16
1.3. Властивості залишків методу найменших квадратів
Позначимо через
ˆ
,1,
t
tn різниці між фактичними та теоретичними, тобто
обчисленими з рівняння вибіркової регресії (1.8) значеннями залежної змінної:
ˆ
ˆ
ˆˆ
()
tttt t
yy y
x (1.9)
Тоді величину
ˆ
t
називатимемо залишками методу найменших квадратів.
Залишки можна вважати вибірковими, або емпіричними аналогами збурень. З
урахуванням уведених позначень перше нормальне рівняння слід записати у вигляді
1
ˆ
0
n
t
t
(1.10)
Отже, сума залишків методу найменших квадратів дорівнює нулю.
Друге нормальне рівняння набуде вигляду
1
ˆ
0
n
tt
t
x
(1.11)
Або якщо позначити через
x
вектор значень незалежної змінної, а через
ˆ
ε
вектор
залишків
1
2
n
x
x
...
x
x
,
1
2
ˆ
ˆ
ˆ
...
ˆ
n
ε
,
то
ˆ
(
,
)
0x . Іншими словами, залишки методу найменших квадратів ортогональні до
регресора.
1.4. Розклад дисперсії залежної змінної. Коефіцієнт детермінації
Мета регресійного аналізу – не лише знайти оцінки коефіцієнтів регресії, а й пояснити,
як поводиться залежна змінна. Розкид значень залежної змінної
y
у будь-якій вибірці
можна сумарно описати за допомогою вибіркової дисперсії. Треба вміти розраховувати
величину цієї дисперсії.
З рівнянь (1.8) та (1.9) випливає, що
ˆ
ˆˆ
,1,
ttt
y
xtn (1.12)
Запишемо другу з формул (1.7) у вигляді
ˆ
ˆ
y
x
(1.13)
Від кожного з рівнянь (1.12) віднімемо рівняння (1.13):
ˆ
ˆ
()
,1,
ttt
yy
xx t n (1.14)
Кожне з рівнянь (1.14) піднесемо до квадрату та почленно додамо. Маємо
2222
11111
22
1
ˆˆ
ˆˆˆ
() () 2 2
ˆ
ˆ
nnnnn
tyy t ttt t
ttttt
n
xx t
t
yy S xx x x
Se
, (1.15)
унаслідок (1.10) та (1.11).
Позначимо
1
ˆ
ˆ
n
t
t
y
y
n
. З (1.10) випливає, що
ˆ
yy
. Тому
ˆˆ ˆˆ
ˆ
()()
tttttt
yyyy yy yy
.
Порівнюючи останнє рівняння з (1.14), бачимо, що
ˆ
ˆˆ
()
tt
xx
yy
,
отже
22
1
ˆ
ˆˆ
()
n
xx t
t
S
yy
.
Уведемо такі позначення:

17
2
1
()
n
yy t
t
TSS S
yy
– загальна сума квадратів;
22
1
ˆ
ˆˆ
()
n
xx t
t
ESS S y y
– пояснена сума квадратів;
2
1
ˆ
n
t
t
RSS
– сума квадратів залишків.
Загальна сума квадратів пропорційна до вибіркової дисперсії залежної змінної.
Пояснена сума квадратів пропорційна до вибіркової дисперсії незалежної змінної. Отже,
дисперсія залежної змінної складається із двох частин. Перша виникає завдяки розкиду
значень незалежної змінної, тобто цю частину слід пояснювати за рахунок моделі (звідси і
назва – пояснена сума квадратів).
Друга частина – сума квадратів залишків – виникає
внаслідок збурень; її не можна пояснити за рахунок моделі. Записавши співвідношення
(1.15) з урахуванням уведених позначень, одержимо
формулу розкладу дисперсії
.TSS ESS RSS
(1.16)
Природним бажанням дослідника є максимізувати величину поясненої дисперсії та
мінімізувати величину непоясненої. Для аналізу ефективності розв'язку такої задачі
вводять
коефіцієнт детермінації
2
R , який визначають як частку поясненої і загальної
сум квадратів
2
1
ESS RSS
R
TSS TSS
(1.17)
Для обчислення коефіцієнта детермінації можна скористатися також такими
формулами:
2
2
2
ˆ
ˆ
xy xy
xx
yy yy xx yy
SS
S
R
SSSS
.
Коефіцієнт детермінації є частиною дисперсії залежної змінної, яку можна пояснити за
рахунок моделі, або, іншими словами, завдяки мінливості незалежної змінної. Коефіцієнт
детермінації є мірою щільності саме
лінійного зв'язку між
x
та
y
.
Коефіцієнт детермінації завжди міститься в межах від нуля до одиниці. Чим ближче
2
R до 1, тим точніше
x
пояснює
y
. Якщо
2
1R
, то це означає, що всі значення
x
та
y
лежать на одній прямій. Якщо
2
0R
, то лінія регресії – горизонтальна пряма, що
свідчить про те, що немає лінійного зв'язку між змінними.
Коефіцієнт детермінації можна вважати мірою згоди регресії. За інших рівних умов
бажано, щоб коефіцієнт
2
R був якнайбільшим.
1.5. Властивості оцінок методу найменших квадратів
Використання методу найменших квадратів дозволяє отримати незміщені оцінки
регресії. Показати це досить просто:
22
22
2
2
ˆ
MM
() (
tt t t t t t t
tt tt
tt t t
tt
nxyxynxMyxMy
nx x nx x
nx x x x
nx x
22
22
22
22
()
.
tt tt tt
tt tt
nxnxnx x nx x
nx x nx x
,
11
ˆˆ
ˆ
ˆ
MM M M
()
.
tt
yxyx xx
nn
Можна також показати, що оцінки за звичайним методом найменших квадратів є не
лише незміщеними оцінками коефіцієнтів регресії, але й ефективними в тому разі, якщо
виконано всі наведені вище умови щодо збурень моделі (1.2).

18
Теорема Гауса – Маркова. Для простої лінійної регресії з гомоскедастичними,
некорельованими збуреннями оцінки МНК мають найменшу дисперсію в класі всіх
лінійних незміщених оцінок.
Таким чином, якщо виконано п'ять припущень щодо збурень для простої лінійної
регресії, то дисперсія оцінок буде найменшою серед усіх незміщених оцінок. Неважко
показати, що
2
2
2
2
D;
1
D;
cov
(
,
)
.
xx
xx
xx
S
x
nS
x
S
(1.18)
Наведені формули не можна використовувати для перевірки гіпотез та інтервального
оцінювання, оскільки до них входить невідомий параметр – дисперсія збурень
2
. Можна
показати, що незміщеною оцінкою
2
буде статистика
2
ˆ
2
RSS
n
.
Якщо збурення нормально розподілені, то
ˆ
та
ˆ
– також. Величина
2
1
22
ˆ
(2)
n
t
t
n
RSS
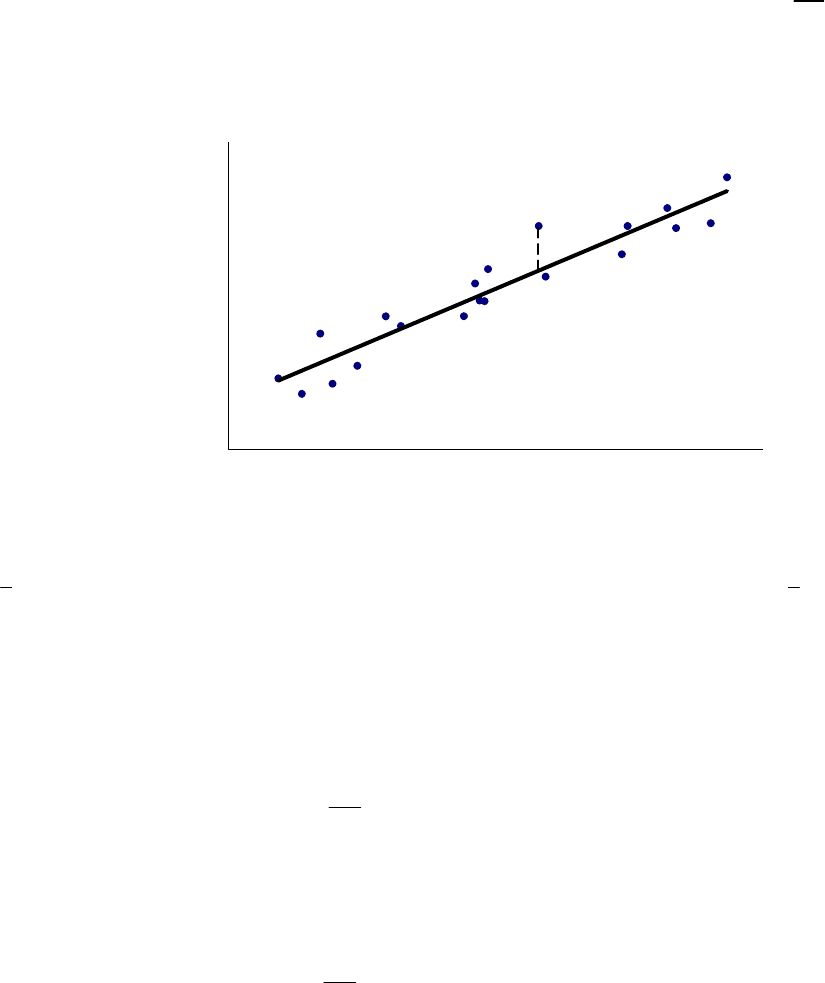
має
2
– розподіл з
2n
степенями свободи. До того ж випадкова величина
RSS
не
залежить від
ˆ
та
ˆ
.
Оскільки
2
ˆ
~N
(
,
)
xx
S
, то
2
ˆ
xx
S
має стандартний нормальний розподіл. Крім того,
2
2
2
~
n
RSS
, і ці випадкові величини незалежні. Отже, частка
2
2
2
ˆ
ˆ
(2)
xx
xx
RSS
n
S
S
має розподіл Стьюдента з
2n степенями свободи. Величина
2
ˆ
xx
S – це оцінка дисперсії
, а
2
ˆ
xx
S – оцінка середньоквадратичного відхилення, або стандартна похибка
оцінки
ˆ
(від англійського standard еrror – стандартна похибка). Уведемо позначення
2
ˆ
s.e.( ) ˆ
xx
S
.
Тоді
2
ˆ
~
ˆ
s.e.( )
n
t (1.19)
Отриманий результат можна використовувати для перевірки різноманітних
статистичних гіпотез.
1.6. Перевірка статистичних гіпотез у моделі простої лінійної регресії
Побудувавши й оцінивши регресію, слід упевнитися в тому, що її можливо
застосовувати на практиці. Для цього регресія має бути адекватною, тобто задовільно
описувати залежність між чинниками, які входять до моделі. З іншого боку, дослідників
цікавить питання про можливість застосовувати модель у подальшому економічному
аналізі. У такому разі слід гарантувати значущість усіх коефіцієнтів регресії.

19
Процес перевірки гіпотез доволі простий. Спочатку за умови прийняття гіпотези
розраховують певну критичну статистику, яку порівнюють із теоретичним значенням з
таблиці відповідного розподілу.
1.6.1. Перевірка адекватності регресії
Навіть якщо між y та x немає залежності, за будь-якою вибіркою спостережень може
здатися, що така залежність існує, хоча й слабка. Лише за випадковим збігом обставин
вибіркова коваріація точно дорівнюватиме нулю, сигналізуючи про те, що немає суттєвої
залежності. На практиці лише випадково коефіцієнт кореляції та коефіцієнт детермінації
2
R
дорівнюватимуть нулю. Відомо, що при близьких до 0 значеннях коефіцієнта
детермінації регресія зазвичай буде неадекватною. Проте як визначити межу, за якою
класифікувати регресії?
Гіпотезу слід формулювати таким чином:
2
0
2
1
:0;
:0.
HR
HR
Адекватність регресії (прийняття гіпотези
1
H ) означає, що незалежні змінні впливають
на залежну змінну. Таким чином, у випадку простої лінійної регресії достатньо перевірити
гіпотезу про
ˆ
0 або
2
0R . Можна показати, що
2
2
1
~1, 2
1
2
pr
R
FFn
R
n
за умови, що 0 .
Таким чином, щоб перевірити гіпотезу, треба:
1.
Обрахувати коефіцієнт детермінації регресії.
2.
Обчислити значення
pr
F .
3.
Знайти в таблиці розподілу Фішера (див. додаток) статистику
teor
F
з 1 та 2n
степенями свободи для заданого рівня значущості
(не плутати з коефіцієнтом у лінії
регресії).
4.
Порівняти знайдені величини: якщо
pr teor
FF
, то модель слід уважати
неадекватною, якщо ж
teor
FF
, то модель адекватна.
1.6.2. Гіпотеза про значущість кореляції між змінними регресії
Ще одним способом перевірки доказу існування залежності між змінними регресії є
оцінювання коефіцієнта кореляції між ними. Щільність зв'язку між змінними визначає
лінійний коефіцієнт парної кореляції, який знаходять за формулою
ˆ
x
xy
yxy
y
xx
y
r
,
де
1
tt
y
xx
y
n
;
22
1
()
xt
xx
n
;
22
1
()
yt
yy
n
.
Очевидно, що величина коефіцієнта парної кореляції завжди за абсолютною
величиною не перевищує 1
(
11
)
xy
r . Що ближче це значення до 1, то сильніший
прямий зв'язок між змінними; що ближче це значення до -1, то сильніший обернений
зв'язок між змінними. Зв'язок слід уважати слабким, якщо значення
xy
r близьке до 0.
На практиці для перевірки гіпотези
0
1
:0;
:0
xy
xy
Hr
Hr
слід обрахувати статистику
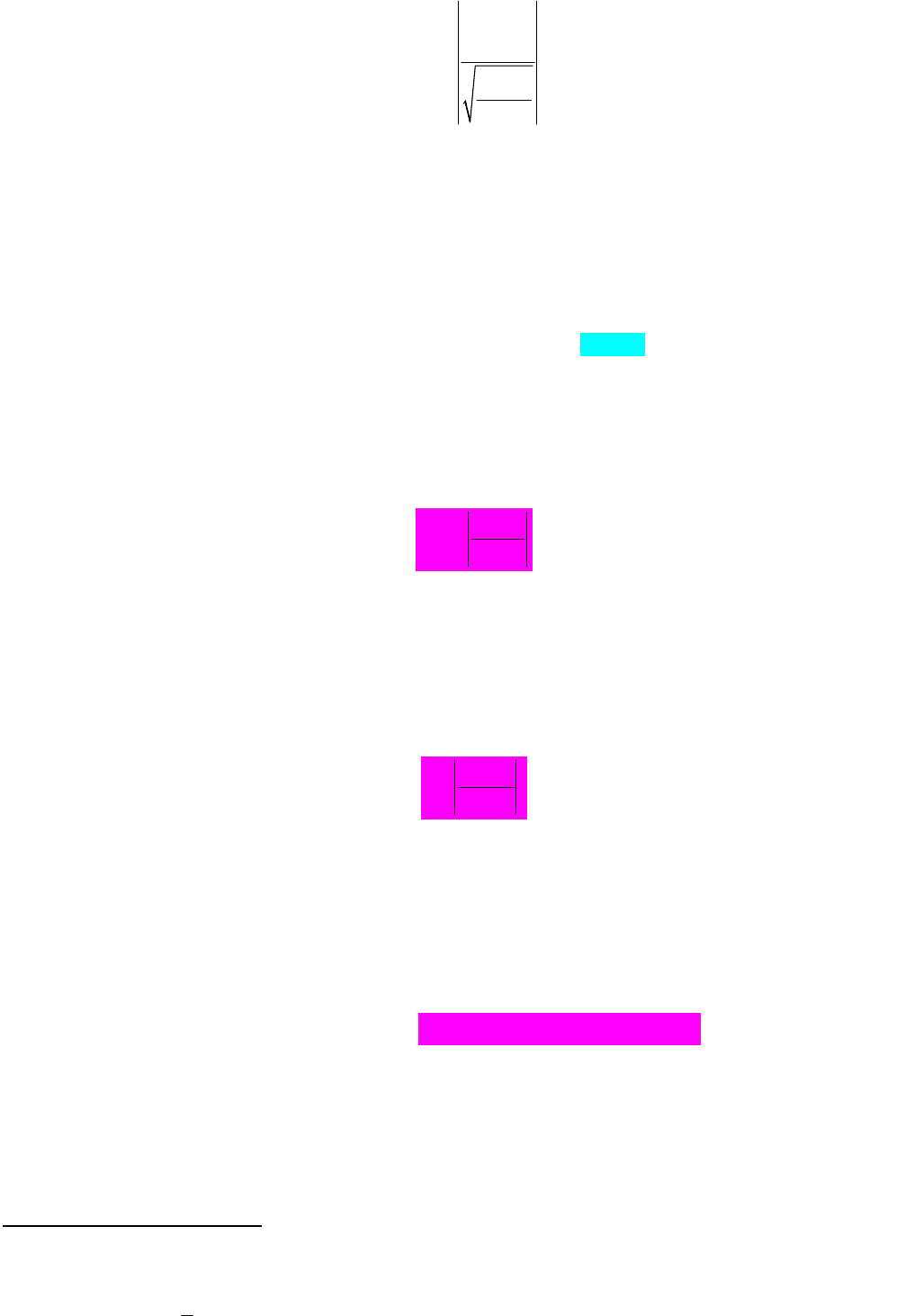
20
2
1
2
xy
pr
xy
r
t
r
n
і порівняти зі статистикою Стьюдента з
2n
степенями свободи:
2,1
teor
ttn
1.
Якщо
teor
tt , то гіпотезу
0
H можна прийняти, тобто залежність між змінними
x
та y
статистично незначуща.
1.6.3. Перевірка гіпотез про коефіцієнти регресії
Стандартною процедурою є перевірка гіпотези про те, що коефіцієнт нахилу
регресійної прямої дорівнює нулю. Прийняття цієї гіпотези означає, що незалежна
змінна не має впливу на залежну (не має впливу в межах лінійної моделі, тобто не
виключено, що насправді між змінними існує залежність, але виражена іншою
функціональною формою).
Пряму й альтернативну гіпотези формулюють таким чином:
0
1
:0;
:0.
H
H
Статистика для перевірки гіпотези має вигляд
ˆ
ˆ
s.e.
()
pr
t
Значення цієї статистики зазвичай автоматично підраховують у комп'ютерних
програмах із регресійного аналізу.
Отриману величину порівнюють зі значенням
teor
t
, яке знаходять із таблиці розподілу
Стьюдента з 2n степенями свободи й рівнем значущості 1
. Якщо
teor
tt , то гіпотезу
0
H приймають, якщо ж
teor
tt , то гіпотезу
0
H відхиляють.
Аналогічно перевіряють гіпотезу про рівність коефіцієнта регресії довільному значенню
m. Зокрема, для перевірки гіпотези
0
:Hm
використовують таку статистику:
ˆ
.
ˆ
s.e.
()
m
t
Отриману величину слід порівняти зі значенням
teor
t
, знайденим із таблиці розподілу
Стьюдента з 2n степенями свободи та рівнем значущості 1. Якщо
teor
tt
, то
гіпотезу
0
H приймають, якщо ж
teor
tt , то гіпотезу
0
H відхиляють.
Показані вище розрахунки свідчать, що якщо оцінка коефіцієнта
ˆ
міститься в
певному інтервалі, то це гарантує прийняття відповідної гіпотези. Величину такого
надійного інтервалу неважко обрахувати:
для коефіцієнта
:
teor teor
ˆˆ ˆˆ
[s.e.() ;s.e.() ]tt
,
для коефіцієнта
:
teor teor
ˆˆ ˆˆ
[
s.e.
()
;s.e.
() ]
tt. (1.20)
Величину
teor
t знаходять із таблиці розподілу Стьюдента з
2n
степенями свободи та
рівнем надійності
1
. Будь-яке гіпотетичне значення оцінки
ˆ
* , що задовольняє
співвідношенню (1.20), буде автоматично сумісним з оцінкою
ˆ
, іншими словами, не
суперечитиме їй. Множина всіх цих значень, визначених як інтервал між нижньою й
верхньою границями нерівності, відома як надійний інтервал для величини
.
1 У всіх формулах цього підручника використано двобічний розподіл Стьюдента. Як відомо, усі статистичні
програми розраховують однобічний розподіл Стьюдента. Щоб уніфікувати відповіді, під час використання
комп’ютерних програм треба застосовувати модифікований рівень надійності: замість величини
1
слід
використовувати
2
1
.
